基于小波分析的滚柱直线导轨副摩擦力波动分析
2016-11-03马洪君1宋现春1姜洪奎1许向荣1高山龙1荣柏松2伟2
马洪君1,宋现春1,姜洪奎1,许向荣1,高山龙1,荣柏松2,杜 伟2
(1.山东建筑大学,机电工程学院,济南 250101;2.山东博特精工股份有限公司,山东 济宁 272071)
基于小波分析的滚柱直线导轨副摩擦力波动分析
马洪君1,宋现春1,姜洪奎1,许向荣1,高山龙1,荣柏松2,杜伟2
(1.山东建筑大学,机电工程学院,济南250101;2.山东博特精工股份有限公司,山东 济宁272071)
滚柱直线导轨摩擦力的波动对滚柱直线导轨的可靠性和稳定性有着重要影响。对采集的摩擦力信号进行多尺度小波变换,再经Hilbert变换和快速傅里叶变换,得到各尺度的频谱。结合滚柱直线导轨的结构及运行特征建立摩擦力数学模型。通过对实验数据与理论模型的对比,证明数学模型的合理性,分析得出承载滚柱数目的变化是滚柱直线导轨摩擦力产生波动的主要原因。
滚动直线导轨 摩擦力 小波分析
MA Hong-jun1,SONG Xian-chun1,JIANG Hong-kui1,XU Xiang-rong1,GAO Shan-long1,RONG Bai-song2,DU Wei2
(1.School of Mechanical and Electronic Engineering, Shandong Jianzhu University, Jinan 250101,China;2.Shandong Best Precision Co.,Ltd.,Jining Shandong 272071,China)
0 引言
滚动直线导轨作为数控机床的关键功能部件,具有摩擦力小、运行平稳、定位精确等特点,其性能的优劣直接会影响到数控机床的性能及可靠性。摩擦是导轨主要的能量损耗方式,摩擦力的变化不仅会影响滚动直线导轨运行的平稳性,更对导轨的功能可靠性和精度保持性有着重要影响[1]。
随着数控机床的不断发展,国内外专家学者对滚动直线导轨也进行了深入的研究。角田和雄基于赫兹接触理论得出了滚动直线导轨在两点接触时差动滑动的摩擦力计算公式,又进一步推导出了流体摩擦力的计算公式[2]。须田稔和石川义熊对摩擦力的计算公式进行推导并加以实验验证,研究发现当滚珠刚进入非承载区时摩擦力最大,外加载荷越大平均摩擦力也越大[3-4]。NSK公司开发了一种K1密封件,可在运行过程中缓慢释放润滑油,在高速、重载及有污染的情况下仍然有极佳的润滑效果[5]。
荣柏松在虚拟样机技术分析软件AD-AMS环境下对滚柱直线导轨副进行动态仿真研究,建立结构参数及性能与仿真输出结果联系,对结构参数进行优化设计[6]。钟洋针对滚柱直线导轨副精度保持性问题,对其在加载条件下运动精度损失过程进行建模与试验研究[7]。江南大学的高永坤通过理论分析和有限元模拟仿真,研究了滚动直线导轨过盈量和摩擦特性的关系[8]。华中科技大学耿宝龙分析了滚珠直线导轨摩擦力的形成机理,并对垂直正压载荷、前后扭转和左右扭转三种情况下的摩擦力进行的分析计算[9]。
国内外专家学者对滚动直线导轨摩擦力进行了大量的分析研究并获得了丰富的成果。本文基于小波分析方法,分析了滚柱直线导轨在运行中摩擦力产生波动的原因,为提高导轨运行的可靠性和稳定性提供指导。
1 滚柱直线导轨副摩擦力测量装置
实验装置采用博特精工直线导轨综合性实验台,如图1。

图1 直线导轨综合性实验台

1.控制柜 2.直线电机 3.高速静音导轨 4.被测导轨 5.温度传感器6.直线电机滑台 7.拉压传感器 8.连接杆 9.空间球面铰链 10.光栅尺11.实验台床身
图2实验台工作原理图
图2为实验台工作原理图,实验台采用直线电机2驱动,由一副高速静音导轨3支撑直线电机滑台,被测导轨副4直接安装在床身11上,其滑块通过空间球面铰链9、连接杆8与直线电机滑台6连接。通过直线电机带动被测导轨滑块移动。实验台采用西门子数控系统控制直线电机的运动,光栅尺10对滑台的位置实时检测反馈。滑台与连接杆之间设有拉压传感器7。根据滑块匀速运动时物体受力平衡的原理,滑块在匀速运行时拉压传感器7的读数即为导轨的摩擦力。拉压传感器通过变送器、PIC数据采集卡与工控机相连,工控机采用labview编程控制采样频率、采样时间并实时绘制出摩擦力曲线以及对数据进行后期处理。实验台最大行程可达3000mm,最大加速度为3g,最大运行速度为5m/s。实验中滑块运行速度为100mm/s,拉压传感的采样频率为20Hz。实验导轨采用博特精工的ZL型JSA-LZG45号滚柱直线导轨。滚柱尺寸为5mm×7mm,滚柱在保持链上的中心间距为6mm,每个滚道中有47个滚柱,滑块的长度为102mm。
2 小波理论分析
2.1离散小波变换
1974年法国工程师J.Morlet首次提出小波变换的概念[10]。1986年数学家Y.Meyer构造出了真正了母小波[11]。在传统信号处理中,常采用傅里叶变换,它是将信号由时域转化为频域进行分析,但是变换后丢失的时域信号信息,存在缺陷。相比传统的傅里叶变换,小波变换可以在时域和频域同时分析。
在实际应用中,常采用离散小波分析,其计算公式为:
(1)
(2)

其中Cj,k表示离散化小波系数,ψj,k(t)表示离散小波函数,a表示离散后的尺度参数,b表示离散后的平移参数。
2.2多分辨率小波分解
多分辨率小波分解主要原理如下。
将空间逐级二分为一组相互正交的子空间:
V0=V1+W1,V1=V2+W2,…,
Vj=Vj+1+Wj+1,…
(3)
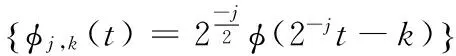
(4)
(5)
可以看出Pjf(t)为f(t)在子空间上的平滑逼近,Djf(t)为f(t)在子空间上的细节分量。
2.3实验数据小波分析
对采集的摩擦力数据进行多尺度小波分析,采用Daubechies小波系列,该小波函数具有较好的紧支撑性、光滑性和近似对称性。经过反复实验,采用第4序列db4小波函数效果最好,分解尺度为4,得到图3的分解结果。再分别对各尺度进行Hilbert变换和快速傅里叶变换,得到如图4结果。

图3 实验数据多尺度小波分析

图4 实验数据小波谱分析
图3中可以看出,摩擦力信号在格尺度上具有明显的周期性。相应的在图4谱分析中,各尺度上频率比较集中,各尺度上频率的分布如表1。

表1 实验数据小波分析主要频率
由表1可以看出,摩擦力信号的低频成分主要集中在0.33Hz、0.66Hz、1.6Hz和3.6Hz,高频成分主要集中在6.3Hz和8.33Hz。在以100mm/s速度运行的时候,保持链在循环轨道中的运行频率正好是0.33Hz,而滚柱进出承载区的频率为16.66Hz正好是8.33Hz的倍数。因此初步断定承载滚柱个数的变化是影响摩擦力波动的原因。
3 滚柱直线导轨副摩擦力数学模型与分析
3.1摩擦力数学模型
帕姆格林公式对滚柱变形的趋近量计算为[12]:
(6)
(7)
(8)
反推出滚柱的正压力为:
(9)
导轨施加预紧力的方式为滚柱的直径略大于滚道的高度,故每个滚柱的接触面相互趋近量是一定的,故在无载荷的情况下,每个滚柱所受正压力是一定的,摩擦力也是一定的。可求出导轨所受摩擦力为:
f=4ZμFn+(47-Z)F+F′
(10)
(11)
其中Z为承载滚柱个数,F为单个滚柱在非承载区的摩擦力,F′为保持链在滚道中所受摩擦力。

f=KZ+F1
(12)
假定滑块初始位置为图5中的滑块位置,向左移动,即保持链的第一个滚柱刚好没有离开承载区,则承载滚柱数Z在一个周期内随位移的变化函数为:

(13)

图5 滚柱在滚道中的排布
当缺口位于非承载区时,承载滚柱数为17和18之间波动,周期为6mm。当缺口处有非承载区运行到承载区的时候,承载滚柱个数每运行6mm减少一个直到减少到14个,缺口完全进入承载区。当缺口在承载区运行时,承载滚柱数为14和15之间波动,周期为6mm。缺口离开承载区时,每6mm增加一个承载滚柱,直到18个,如图6所示。

图6 承载滚柱数随位移的变化
3.2摩擦力数学模型小波分析
运行速度为100mm/s,取承载滚柱数变化函数的三个周期,采用与实验数据相同的处理方法分析,得到如图7、图8的结果。

图7 摩擦力理论模型小波分析

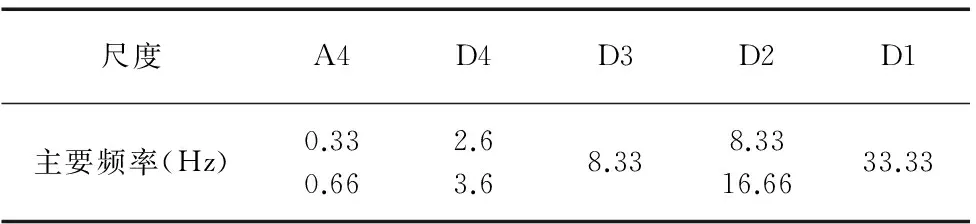
图8 理论模型小波谱分析
尺度A4D4D3D2D1主要频率(Hz)0.330.662.63.68.338.3316.6633.33
通过图3与图7对比,小波分解后的实验数据与数学模型信号的平滑逼近分量A4具有同样的走势和周期。图8中信号在各尺度上波动频率比较集中,分别为0.33Hz、3.6Hz、8.33Hz、16.66Hz和33.33Hz,如表2。表1与表2对比可以发现,实验数据分析得到的频谱同样集中在0.33Hz、3.6Hz和8.33Hz上,而16.66Hz与33.33Hz为8.33Hz的倍频。由此可以证明数学模型与实验数据具有一致性,可以反应实际摩擦力波动的特性,是合理性,并可以证明承载滚柱个数的变化是影响滚柱直线导轨摩擦力的主要因素。
3.3时域分析

图9 摩擦力时域图
图9为导轨运行一个行程3m摩擦力随位移的变化图像。图9可以看出摩擦力随位移的变化具有明显的周期性波动,波动周期大致为300mm。而且在每个周期中有100mm左右的位移内幅值较小,200mm左右的位移内幅值较大。保持链长度为285mm,而循环滚道的长度为300mm,这导致了滚柱在滚道循环时并不是均匀分布的。在保持链首尾相接的地方有3个滚柱的缺口,如图5。当缺口部分运行到承载区时,承载滚柱会相对的减少3个,进而引起了摩擦力的减小。缺口在承载区运行的距离为滑块的长度102mm,这正与测量中幅值低的部分对应起来。整个滚道的长度为300mm,缺口在非承载区运行时,承载滚柱相对较多,摩擦力相对增大,运行距离为188mm,这也与实际测量相符。
4 结论
通过对滚柱直线导轨摩擦力的多尺度小波分解,经Hilbert变化和快速傅里叶变换,对测量数据进行了谱分析。结合滚柱导轨副结构特点,对滚柱导轨副中滚柱摩擦力波动原因进行了理论分析,最后通过测量实验验证了理论分析的正确性。主要研究结论如下:
(1)通过对摩擦力信号的小波谱分析,发现摩擦力的波动与承载滚柱的个数有关,进而基于此特点建立数学模型。经过小波谱分析对比,数学模型与实验数据具有相同的频谱特性,能够充分反应摩擦力波动在不同频率上的特性,是合理的。
(2)对滚柱导轨副中滚柱摩擦力波动原因理论分析发现,滚柱导轨摩擦力波动的产生主要是由承载滚柱个数周期性变换引起的。摩擦力的高频波动是由于滚柱在保持链的作用下连续均匀进出承载区,承载数目呈高频变化。摩擦力的低频波动是由于保持链不闭合,使得承载滚柱数目在保持链循环周期中发生低频突变。
(3)建议采用首尾相接的保持链,减少承载滚柱数的突变,可以有效增加导轨运行的平稳性。同时对由于结合面加工制造误差以及安装误差等因素引起的摩擦力波动作进一步的研究。
[1] 冯虎田,杨艳国,王小牧,等. 滚动直线导轨副摩擦力动态测量系统设计[J]. 金属加工(冷加工),2010(20):54-56.
[2] 角田和雄.玉轴受のモメントに关すゐ研究[J].日本机械学会论文集,1961,27(178):945-956.
[3] 石川义雄.须田念直动玉轴受の摩擦力发生の要因[J].精密机械,1981(7):71-78.
[4] 石川义雄.须田念直动玉轴受の摩擦力变动[J].精密机械,1981(12):58-63.
[5] Kato S.直线导轨K1密封件[J]. 陈凯,译.国外轴承技术,2001(3):8-16.
[6] 荣伯松,宋现春,姜洪奎,等. 基于ADAMS的滚柱直线导轨副的动态仿真[J]. 组合机床与自动化加工技术,2011(10):31-35.
[7] 钟洋,陶卫军,韩军. 滚柱直线导轨副精度损失模型及其试验研究[J]. 组合机床与自动化加工技术,2013(1):14-17.
[8] 高永坤. 滚动直线导轨过盈量和摩擦特性关系的研究[D].无锡:江南大学,2013.
[9] 耿宝龙. 滚动直线导轨副摩擦分析及试验方法研究[D].武汉:华中科技大学,2012.
[10] 葛哲学.小波分析理论与MATLAB R2007实现[M].北京:电子工业出版社,2007.
[11] 董长虹,高志,余啸海.Matlab小波分析工具箱原理与应用[M].北京:国防工业出版社,2004.
[12] 耿宝龙. 滚动直线导轨副摩擦分析及试验方法研究[D].武汉:华中科技大学,2012.
(编辑李秀敏)
Friction Force Fluctuation Analysis of Roller Type Linear Guideways Based on Wavelet Analysis
The friction force fluctuation of roller linear guide has important influence on the reliability and stability of the linear guide. Multi-scale wavelet transformation was used in processing the acquired friction signal. Then frequency spectrum of each scale can be obtained, through Hillbert transformation and Fast Fourier transformation (FFT). With structure and operating characteristics of roller linear guide, the friction model was established. The friction model was proved to be reasonable, through the comparison of the experimental data and theoretical model. At last it was found that the main reason of friction force fluctuations was the change in the number of bearing roller.
roller type linear guideways; friction; wavelet anslysis
1001-2265(2016)09-0024-04DOI:10.13462/j.cnki.mmtamt.2016.09.007
2015-09-17;
2015-10-19
“高档数控机床与装备制造基础”国家重大科技专项(2012ZX04002013);国家自然科学基金(51375279);国家自然科学基金青年项目(51205235)
马洪君(1989—),男,山东济宁人,山东建筑大学硕士研究生,研究方向为机电系统控制及自动化,(E-mail)a2280871@163.com。
TH16;TG68
A
