双定子马达滚柱受力特性分析与实验研究
2022-09-19刘巧燕刘忠迅
刘巧燕,刘忠迅
(1.黄淮学院智能制造学院,河南驻马店 463000;2.驻马店市机器人先进流体动力驱动技术重点实验室,河南驻马店 463000)
0 前言
液压技术广泛应用于工程机械、农业机械、矿山机械以及航空航天等领域,其中高端液压元件不仅是完成重大工程项目、重大技术装备的基本保证,也直接决定着机电产品的附加值水平。
近年来,国家对高端高压高速马达关键技术的研发格外重视。如科技部为贯彻落实《国家中长期科学和技术发展规划纲要(2006—2020年)》和国务院《装备制造业调整和振兴规划》等文件精神,在国家科技支撑计划《关键基础件和通用部件》重点项目中将《工程机械静液传感高速高压变量液压泵和马达关键技术研究》列为重点课题,面向工程机械成套液压系统,开发高性能液压泵和马达成套系统,以突破产业化关键技术,增强自主创新能力。
双定子液压多速马达是基于国际专利技术的一种新型液压元件,目前已对双定子系列液压元件进行了大量的研究,但对叶片结构的优化设计还未进行深入的研究。故本文作者以双定子液压马达的叶片为研究对象,对其进行理论分析并进行结构改进。
1 连杆槽为圆弧时滚柱受力分析
双定子液压多速马达有内马达单独工作、外马达单独工作、内外马达联合工作和内外马达差动工作4种不同的工作方式。图1所示为双作用双定子液压马达原理简图。经分析可得,在向外马达的进油口与内马达的进油口分别通入压力油时,与外定子接触的外滚柱存在两种不同的受力状态:外定子曲线大圆弧区与外定子曲线小圆弧区;与内定子接触的内滚柱则存在4种不同的受力状态:差动连接工作下内定子曲线的大、小圆弧区域与非差动连接工作下内定子曲线的大、小圆弧区域。
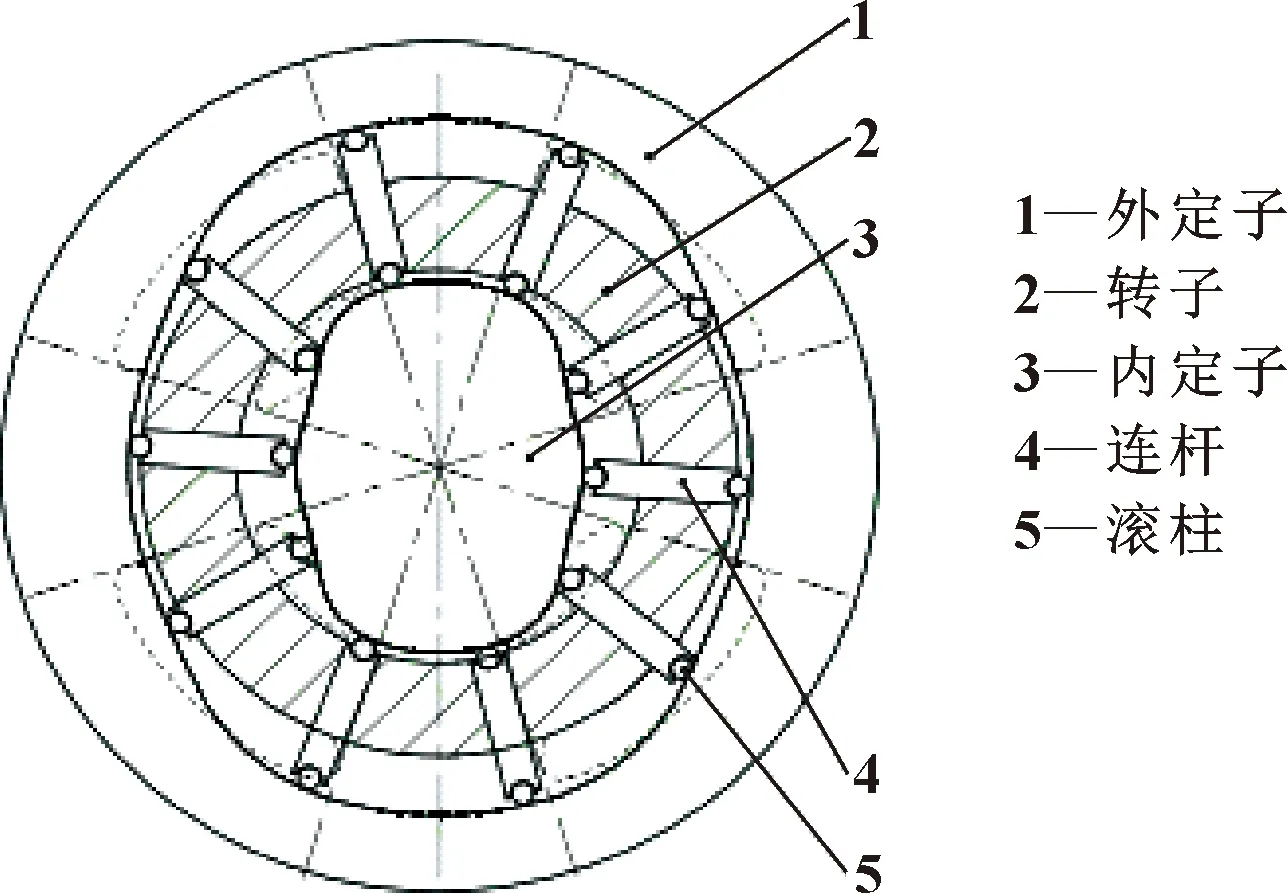
图1 双作用双定子液压马达原理
1.1 大圆弧区外滚柱受力
当双定子液压多速马达运行稳定后,大圆弧区的外滚柱受力情况如图2所示。
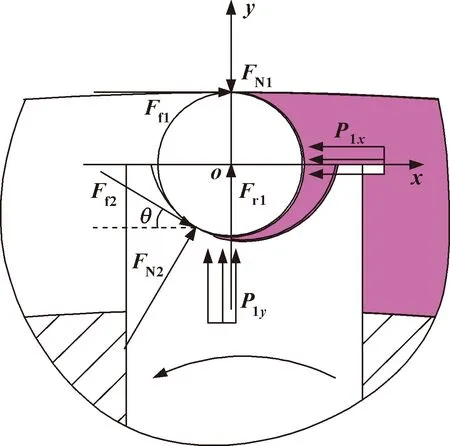
图2 大圆弧区外滚柱受力简图
结合图中滚柱受力情况可列出如下平衡方程:
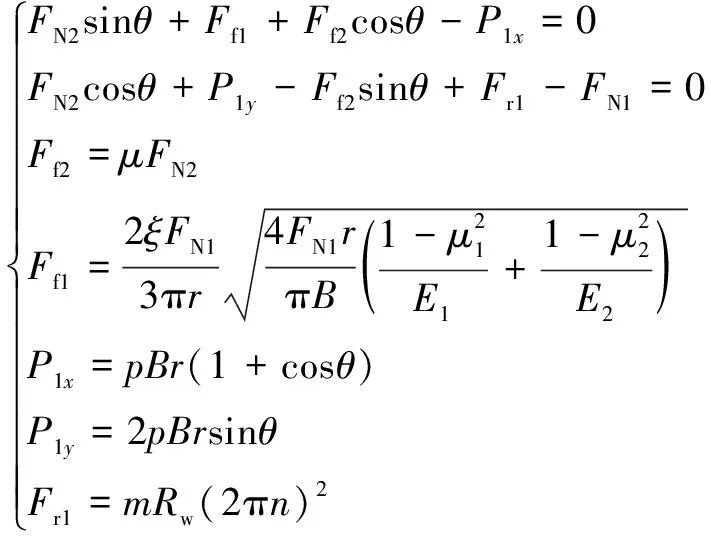
(1)
式中:为离心惯性力;为外定子对滚柱的接触反力;为连杆凹槽对滚柱的作用力;为外定子与滚柱之间的滚动摩擦力;为连杆凹槽与滚柱间的摩擦力;1、1分别为液压油对滚柱的作用力在、方向的分力;为滚柱与连杆凹槽间的滑动摩擦因数;为滚柱质量;为转子转速;为外定子曲线大圆弧半径。
将公式(1)整理可得:
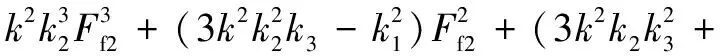

(2)
其中:
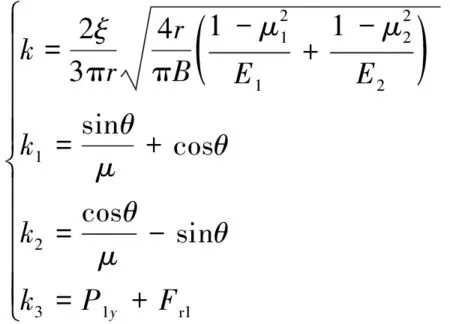
(3)
式中:为滚柱与定子材料间的弹性滞后系数;、分别为滚柱、定子材料的泊松比;、分别为滚柱、定子材料的弹性模量。
1.2 小圆弧区外滚柱受力
当双定子液压多速马达运行稳定后,小圆弧区的外滚柱受力情况如图3所示。
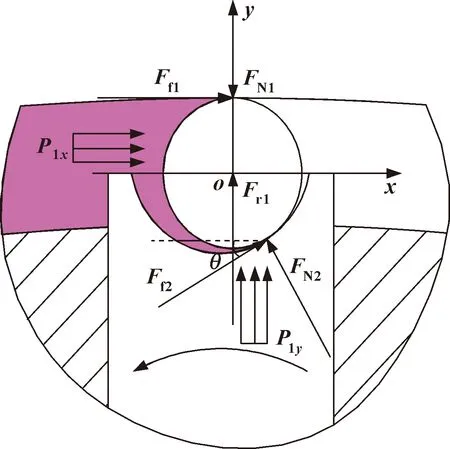
图3 小圆弧区外滚柱受力简图
结合图中滚柱受力情况可列出如下平衡方程:
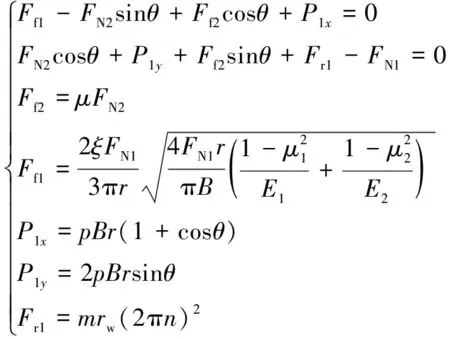
(4)
1.3 差动工作方式下大圆弧区内滚柱受力
当双定子液压多速马达差动连接工作运行稳定后,大圆弧区的内滚柱受力情况如图4所示。
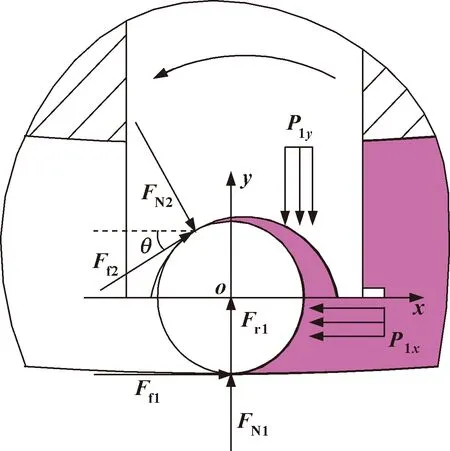
图4 大圆弧区内滚柱受力图(差动工作方式下)
内滚柱的平衡方程为
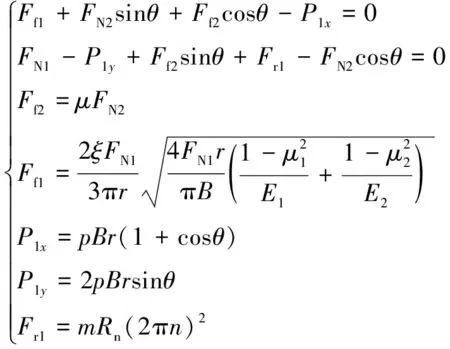
(5)
式中:为内定子曲线大圆弧半径。
1.4 差动工作方式下小圆弧区内滚柱受力
当双定子液压多速马达差动连接工作运行稳定后,小圆弧区的内滚柱受力情况如图5所示。
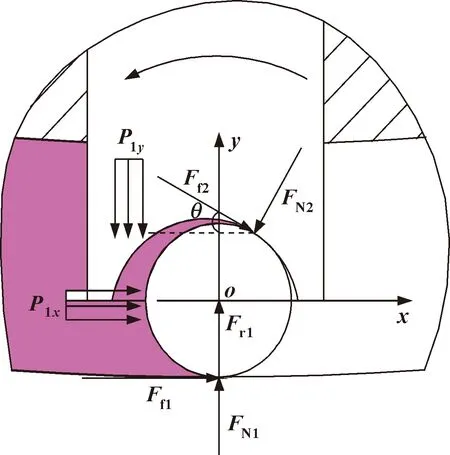
图5 小圆弧区内滚柱受力图(差动工作方式下)
内滚柱的平衡方程为
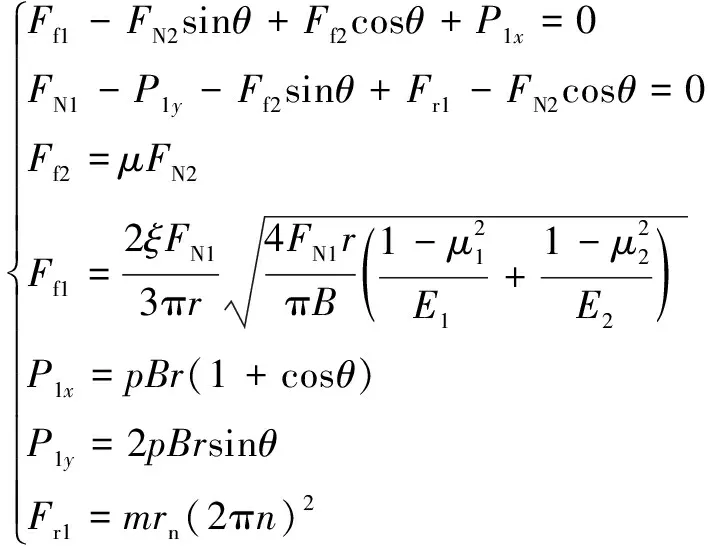
(6)
1.5 非差动工作方式下大圆弧区内滚柱受力
当双定子液压多速马达处于非差动连接工作运行稳定后,大圆弧区的内滚柱受力情况同图5。
内滚柱受力平衡方程为
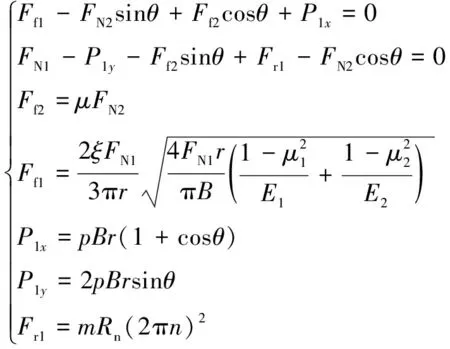
(7)
1.6 非差动工作方式下小圆弧区内滚柱受力
当双定子液压多速马达处于非差动连接工作运行稳定后,小圆弧区的内滚柱受力情况同图4。
内滚柱受力平衡方程为
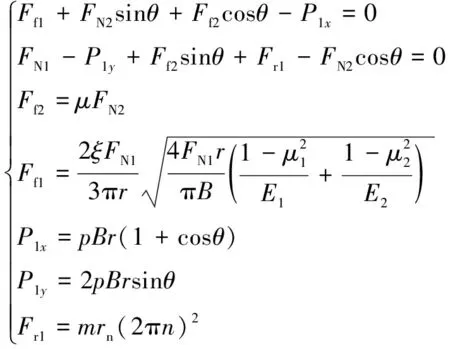
(8)
2 连杆槽为U形时滚柱受力分析
如图6所示,在原有圆弧形连杆槽型线的基础上提出了一种U形连杆槽结构,该曲线由一段圆弧和与之相切的两条线段组成。所以,滚柱在U形连杆槽型线上的运动包含两部分:在圆弧曲面和斜直面上。滚柱在U形连杆槽下的受力分析与在圆弧形连杆槽下类似,因此此处仅分析与外定子曲线接触的外滚柱的受力状况。

图6 U形连杆槽结构
当双定子液压多速马达运行稳定后,大圆弧区的外滚柱受力情况如图7所示。
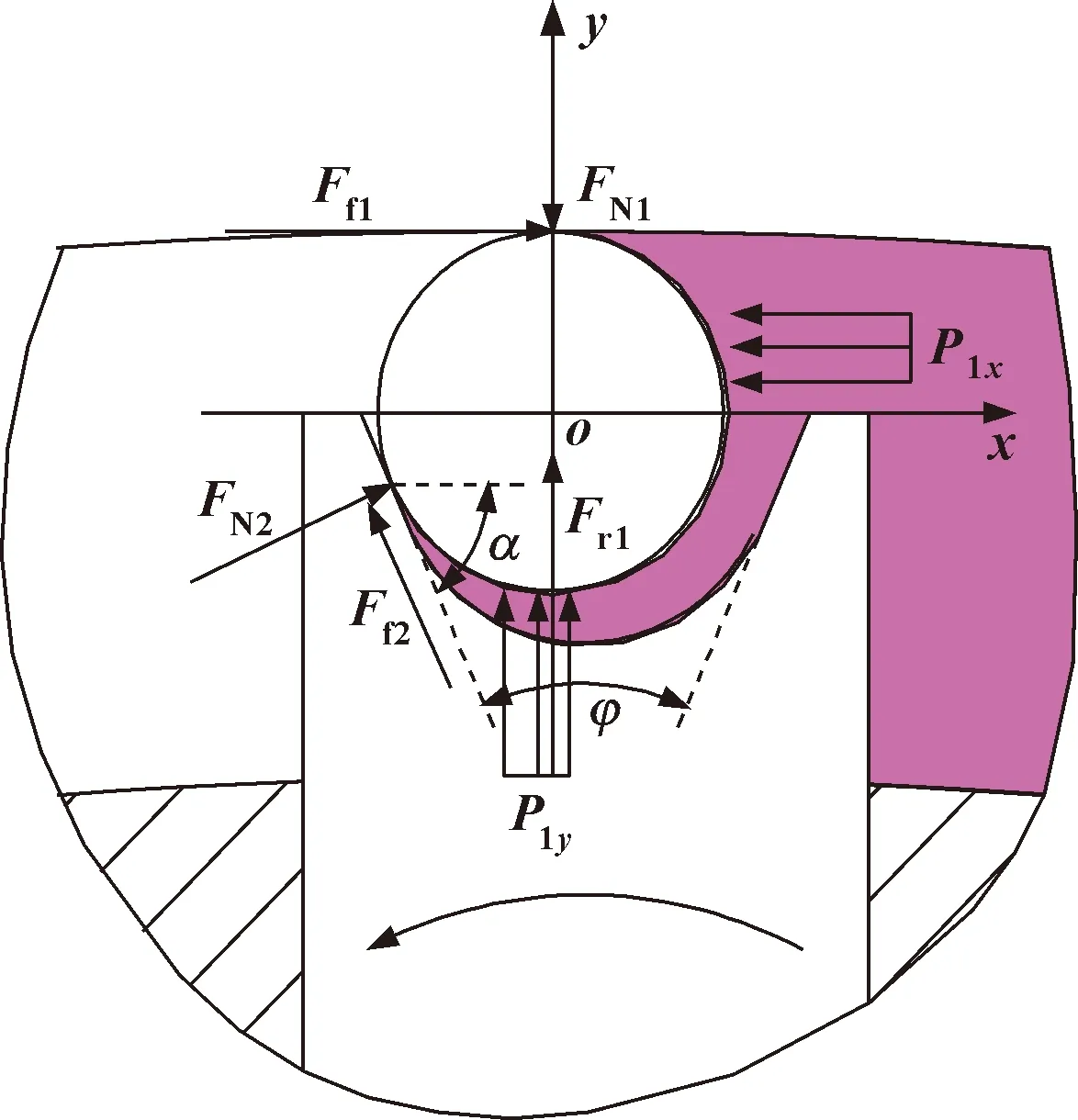
图7 大圆弧区外滚柱受力简图(U形连杆槽)
外滚柱受力平衡方程为
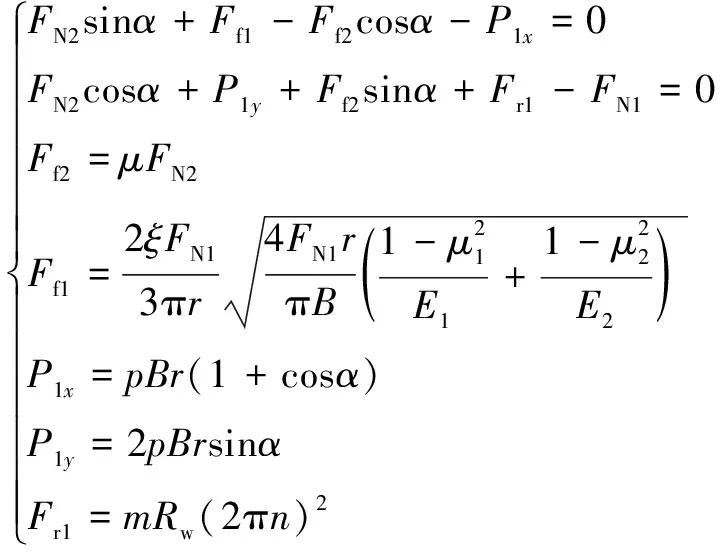
(9)
公式(9)中,与的关系满足以下关系:
=π-2
(10)
当双定子液压多速马达运行稳定后,小圆弧区的外滚柱受力情况如图8所示。

图8 小圆弧区外滚柱受力简图(U形连杆槽)
外滚柱受力平衡方程为
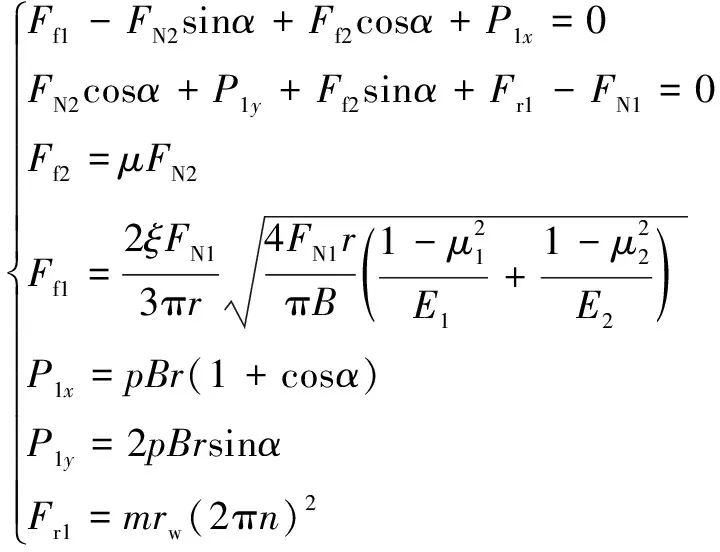
(11)
3 滚柱磨损后的受力状况
在马达运转的过程中,滚柱不可避免地会有磨损。连杆槽型线为圆弧形时,当滚柱偏转角为时,令滚柱的磨损量为Δ,则两者之间的关系为
--(-′)cos=2(-′)=Δ
(12)
式中:′为滚柱磨损后的半径。
当连杆槽型线为U形时,连杆槽型线中的圆弧半径与滚柱半径相等,所以滚柱磨损后应在连杆槽型线的斜直面上,对应的滚柱磨损量为
Δ=2(-′)
(13)
4 实例计算与仿真分析
以双定子多速液压马达样机为例,对滚柱的受力状况进行仿真,可得到如图9—图10所示关系曲线。可以看出:在滚柱偏转角与U形连杆槽斜直面偏角值相同时,滚柱与连杆槽间摩擦力的大小相同。滚柱偏转角越大,滚柱受到的总的摩擦力(滚柱与连杆槽间的摩擦力、定子与滚柱间的摩擦力之和)也越大。然而,逐渐增大的过程也是滚柱磨损越严重的过程,进而也会导致马达的径向间隙补偿能力越来越差。
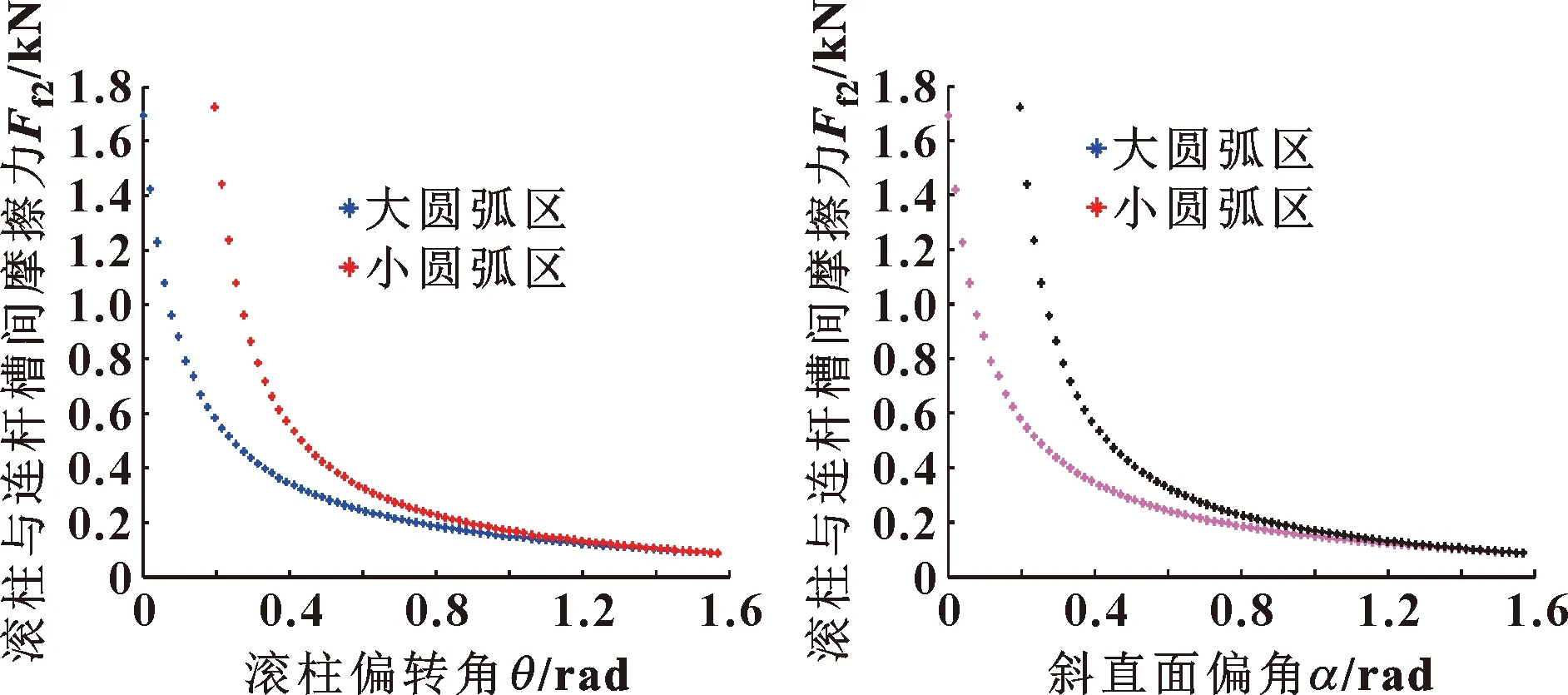
图9 圆弧形连杆槽时大、小圆弧区滚柱和连杆槽间摩擦力与滚柱偏转角的关系 图10 U形连杆槽时大、小圆弧区滚柱和连杆槽间的摩擦力与斜直面偏角α的关系曲线
如图11、图12所示为滚柱与外定子曲线接触时外滚柱的正压力随滚柱磨损量的变化关系。
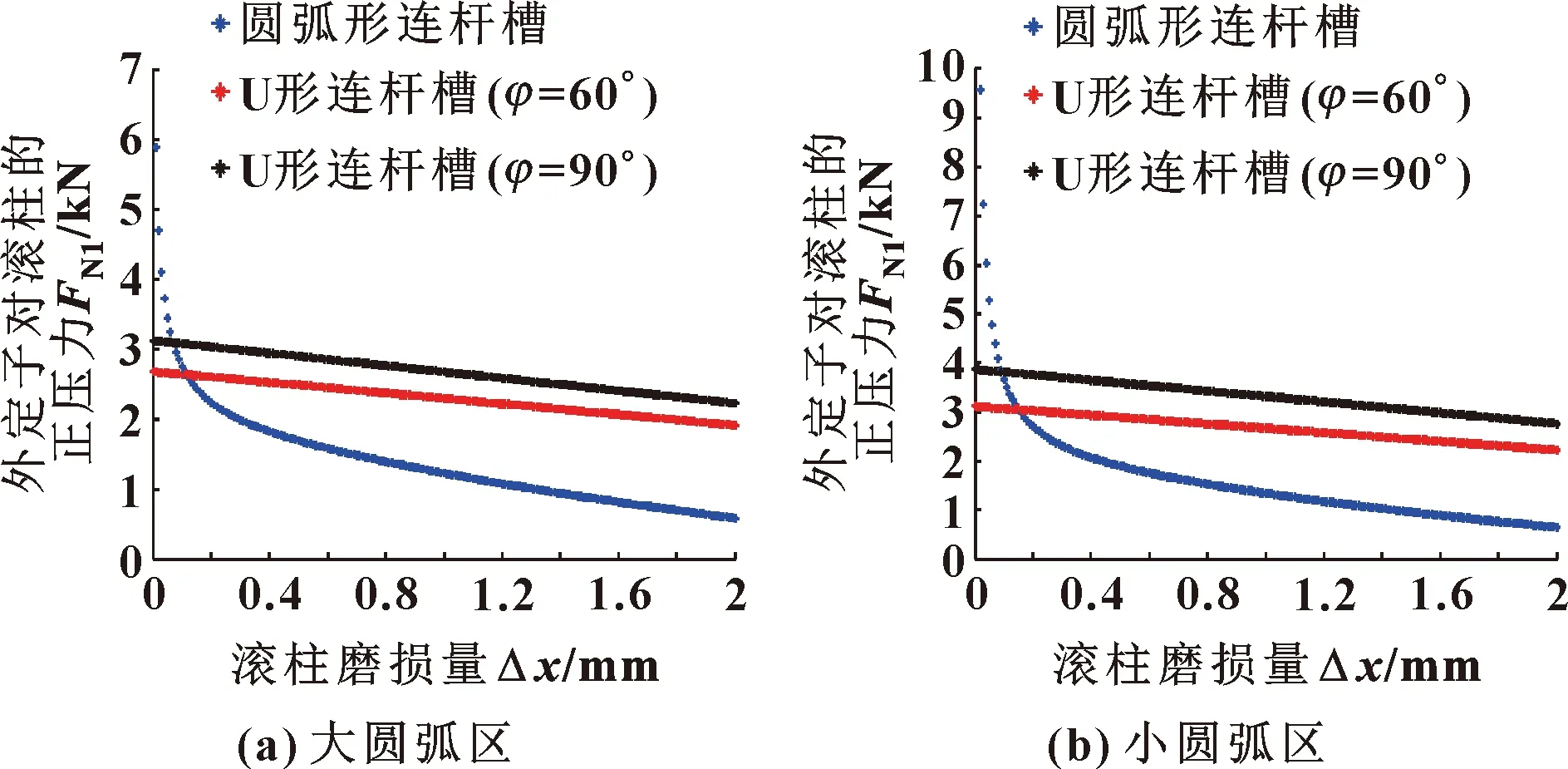
图11 外定子对滚柱的正压力与滚柱磨损量的关系
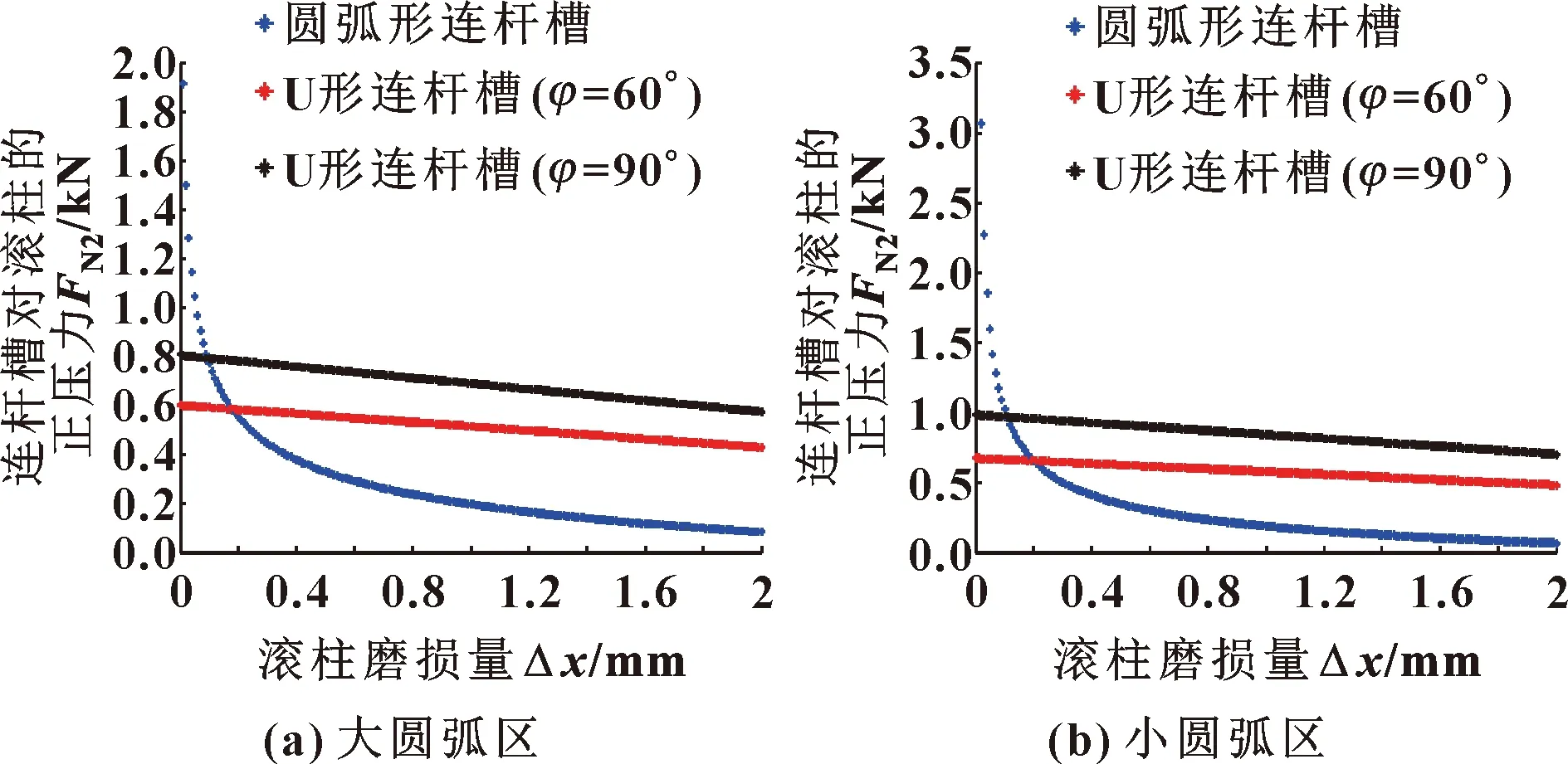
图12 处于外马达中的连杆槽对滚柱的正压力与滚柱磨损量的关系
与内马达定子曲线接触的内滚柱受到的正压力关系曲线如图13—图16所示。
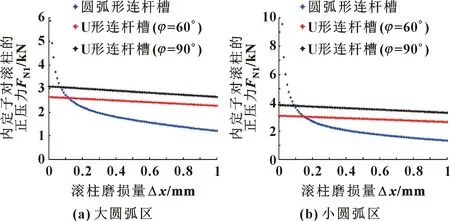
图13 差动连接下内定子对滚柱正压力随滚柱磨损量的变化
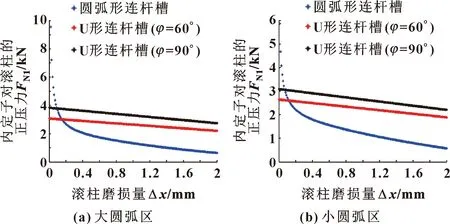
图14 非差动连接下内定子对滚柱正压力随滚柱磨损量的变化
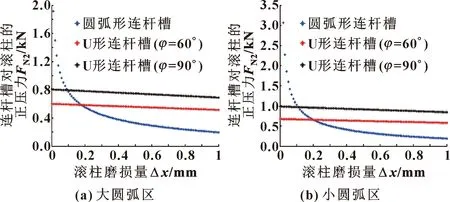
图15 差动连接下处于内马达中的连杆槽对滚柱正压力随滚柱磨损量的变化
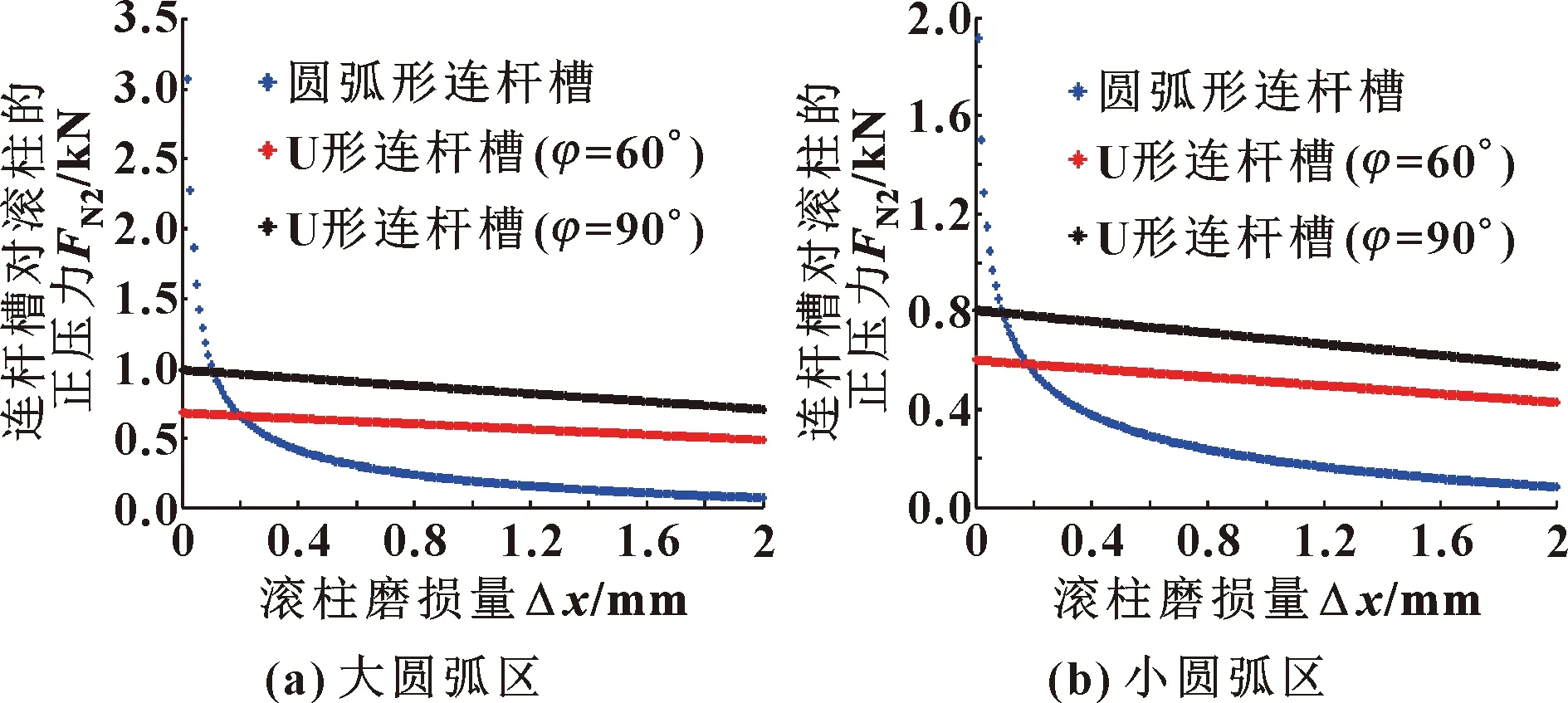
图16 非差动连接下处于内马达中的连杆槽对滚柱正压力随滚柱磨损量的变化
可以看出:在滚柱磨损初期,当连杆槽型线为U形时,与外定子曲线接触的外滚柱所受到的正压力要远小于连杆槽型线为圆弧形时的正压力。随着滚柱不断磨损,滚柱所受到的正压力骤减,这将严重影响到双定子液压马达的密封性能。此外,不论是外滚柱还是内滚柱,当连杆槽型线为U形时,滚柱所受到的正压力与连杆槽型夹角的变化均成正比,且正压力的变化率始终保持不变。所以,U形连杆槽型线结构更有利于双定子液压马达的径向间隙补偿。
5 实验研究
为保证理论分析的正确性,现对U形连杆槽型线的双定子液压多速马达样机进行实验研究。马达样机如图17所示。

图17 双定子马达样机
实验原理和实验平台分别如图18和图19所示。
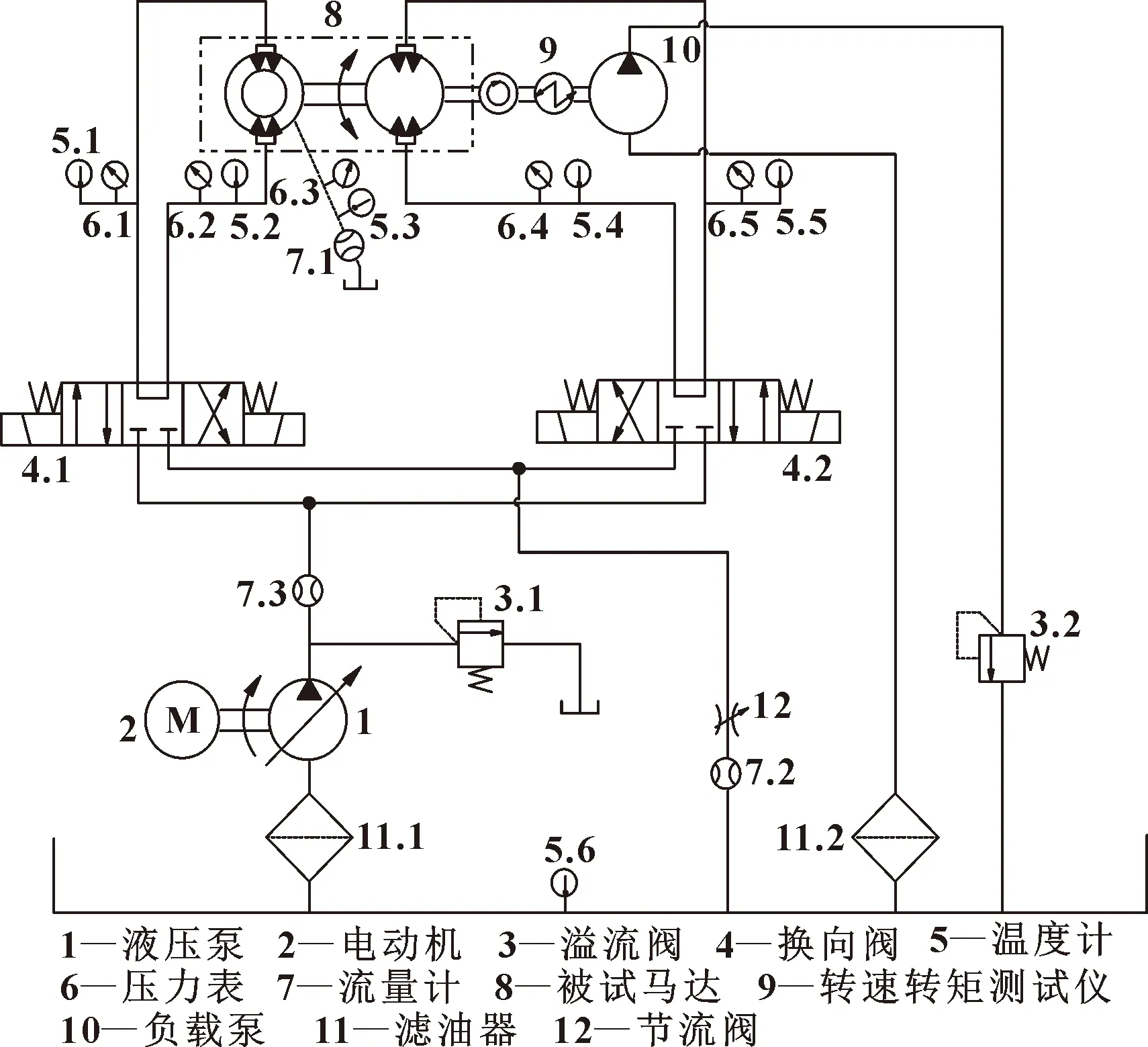
图18 双定子液压马达试验系统原理

图19 样机马达的试验测试系统
样机马达在不同工作方式以及不同外负载下的实验数据如表1—表4所示。

表1 内马达单独工作时的试验数据
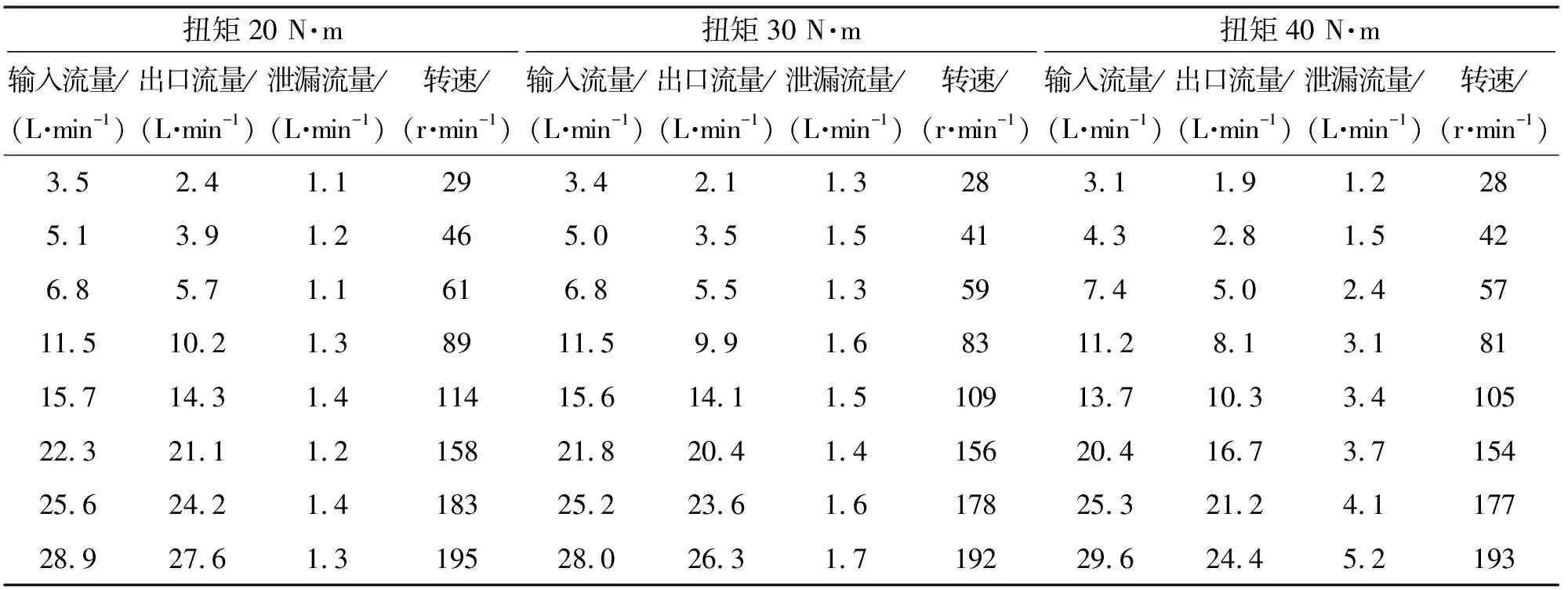
表2 外马达单独工作时的试验数据
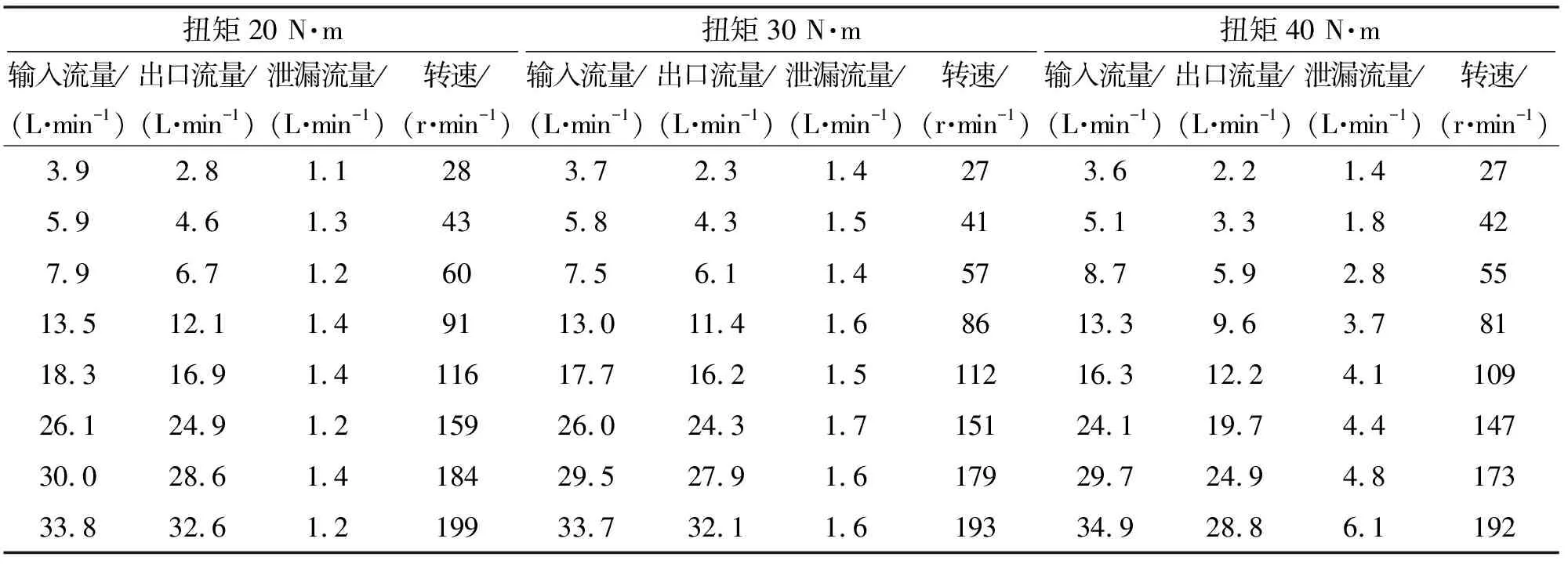
表3 内、外马达联合工作时的试验数据
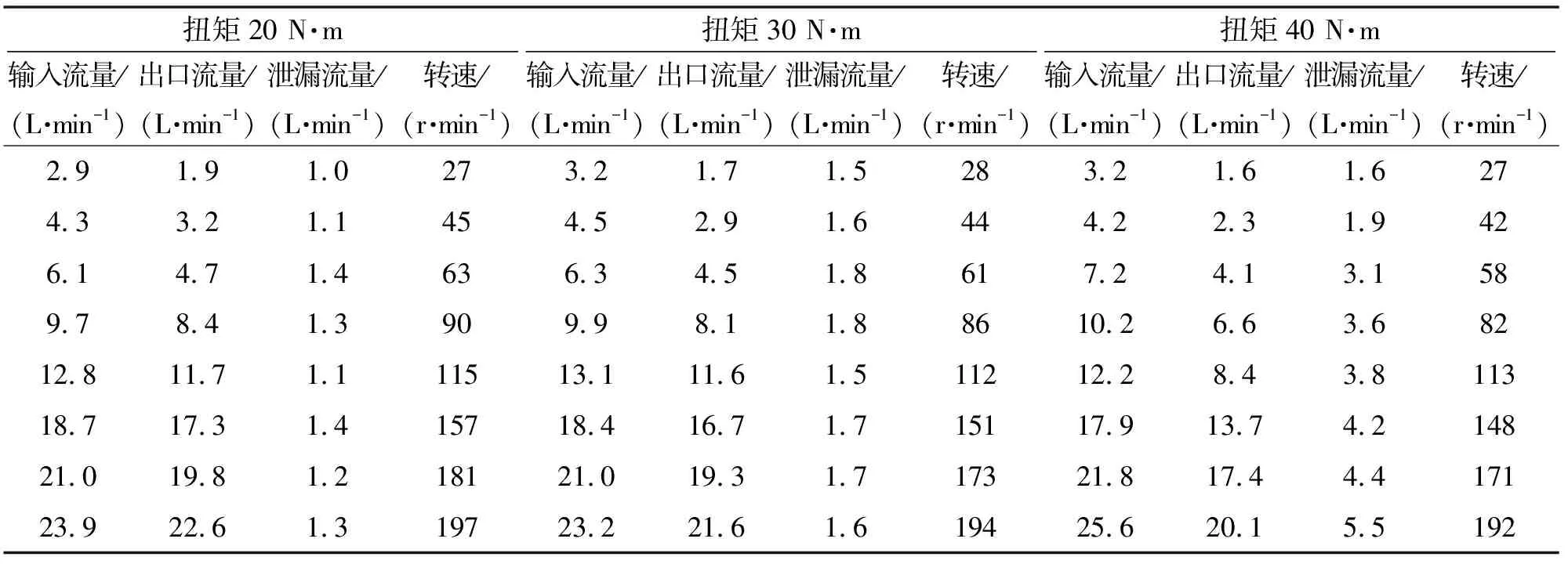
表4 内、外马达差动工作时的试验数据
根据表中实验数据可以得出如图20所示的马达在不同转矩下的容积效率与转速的变化关系。
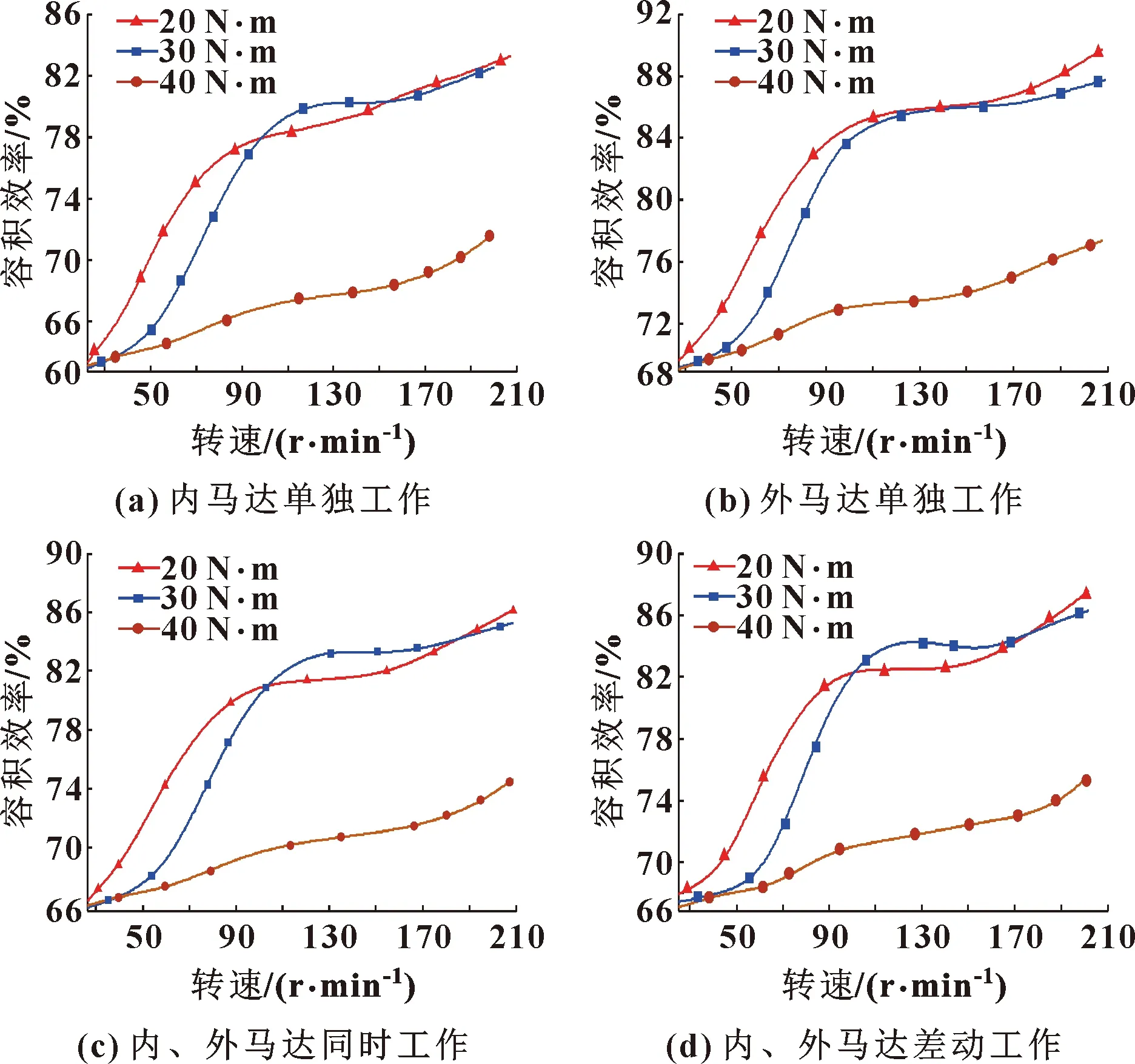
图20 不同转矩下容积效率与转速的关系
从图20可以得出:双定子液压马达在不同外负载下,马达4种不同工作方式下的最大容积效率分别为83.17%、89.63%、86.08%、87.39%。
6 结论
(1)提出一种具有U形连杆槽型线的叶片结构,在满足强度要求的条件下可以使滚柱受力小,提高马达的径向间隙补偿能力,使其工作更具稳定性。
(2)随着滚柱磨损量的增加,滚柱所受正压力逐渐减小,并在U形连杆槽型线的叶片结构下滚柱所受正压力的变化率更加稳定,有利于马达的间隙补偿,提高容积效率。
(3)U形连杆槽叶片结构既使得滚柱与连杆槽间摩擦力减小,又能够在滚柱磨损后保证滚柱偏转角与正压力能够稳定控制在一定范围内变化,实现了双定子马达的可靠密封。
