石英加速度计离心机试验误差系数显著性分析

黄　超，魏宗康，胡荣辉

（北京航天控制仪器研究所，北京100039）

石英加速度计离心机试验误差系数显著性分析

黄超，魏宗康，胡荣辉

（北京航天控制仪器研究所，北京100039）

提出了一种针对石英加速度计精密离心机试验的显著性分析方法。在多位置方法分离加速度计误差系数时，由于激励不足等试验条件的限制，无法保证高次项系数的标定结果正确。离心机试验利用离心机提供的向心加速度作为仪表的输入，能够标定出高次项系数。为了确定被标定的误差系数均具有可信度，有必要对高过载试验结果进行分析，保留可信的误差系数，证明使用的误差模型无误。由于此方法的通用性，在其他试验条件下的误差分离试验中仍可运用。

加速度计；显著性检验；参数辨识；离心机试验

0 引言

为了验证石英加速度计误差模型在高动态条件下的正确性，特别是在大过载情况下对高次项的放大作用，通常采用火箭橇试验、实弹飞行试验、模拟飞行试验、离心机试验等方法。其中，离心机试验利用离心机提供的稳定向心加速度作为仪表的输入，进而将加速度计与高过载有关的误差系数分离出来［1-4］。由于试验条件的限制，不一定所有被标定的误差系数均具有可信度，因此有必要对试验结果进行分析，剔除不可信的误差系数，简化误差模型。

本文研究了石英加速度计离心机试验中误差系数的显著性分析方法，通过实际试验数据验证了此方法的可行性，得出了加速度计离心机试验的显著性误差模型。此方法也可用于其他试验条件下误差模型的显著性检验。

1 石英加速度计离心试验测试系统

精密离心试验的原理是通过将线加速度计通过夹具固定在精密离心机的转盘上，离心机转动使线加速度计敏感质量感受到加速度作用，在不同的转速下，测量合成加速度载荷与测量加速度计输出，即可获得一组加速度载荷及相应的加速度计输出。对于高精度加速度计标定而言，加速度载荷的建模与测量需足够精确。

加速度计的离心试验测试系统包含以下几部分:离心机、加速度计供电电源、加速度计IF测试仪、恒温箱、记录加表模拟量设备、记录加表数字量设备、配套电缆，如图1所示。

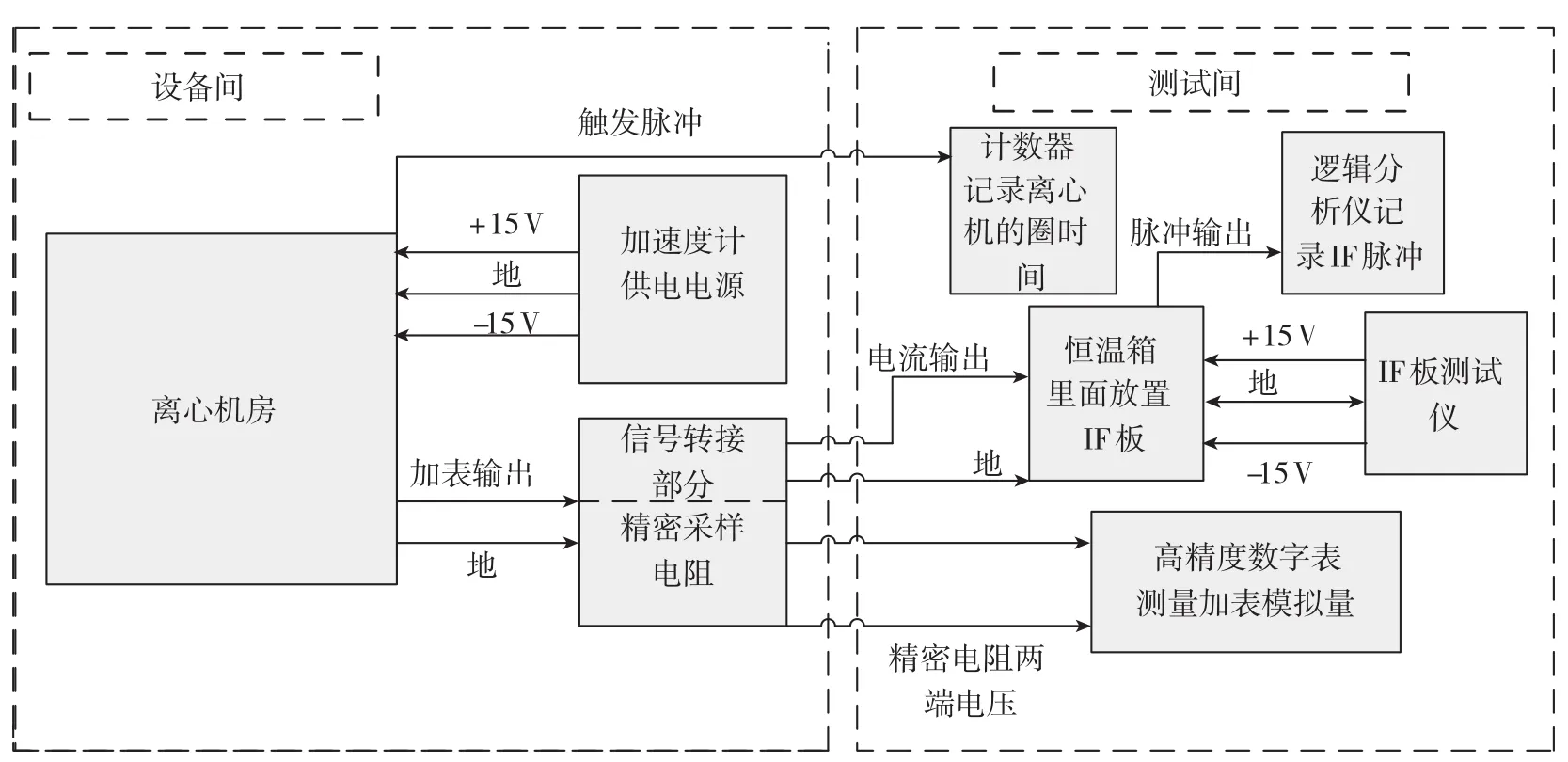
图1　离心测试系统连接简图Fig.1 The combined structure of centrifuge experiment

2 石英加速度计误差模型

加速度计的试验位置取决于需要估计的系数，本试验加速度计的试验位置如图2所示，由位置1和位置2得到的离心机数据来确定误差系数。其中，IA为仪表输入轴，OA为输出轴，PA为摆轴。

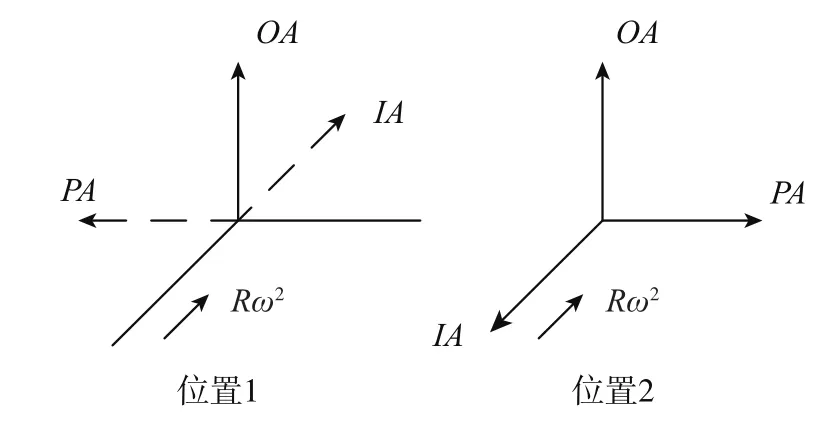
图2　加速度计的安装Fig.2 The installation position of QFPA

由于通过对加速度计两次安装来实现正向和负向加速度的输入，这就带来了很多的系统误差，同时也为精确测试奇异二次项系数造成了困难。

奇异二次项系数主要由以下几个因素产生［5］:

1）精密离心机工作时，转臂的拉伸；

2）转轴在回转运动中，力矩造成转轴的倾斜或偏移；

3）周期性角速度变化；

4）在加速度作用下，加速度计的敏感质量偏移。

虽然加速度计在飞行器上应用时不需要对奇异二次项进行补偿，在进行离心机试验时，在测试模型中加入这一项，是为了保证其他系数的标定精度。由此，给出离心机试验中常用的加速度计误差模型:

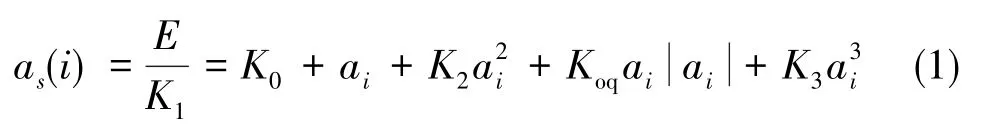
式中，as（i）为第i次试验仪表指示输出；E为传感器输出，ai为第i次试验沿仪表输入轴的加速度；K0为零偏值；K1为标度因数，K2为二次项系数；Koq为奇异二次项系数；K3为三次项系数。

将式（1）进行变形有:

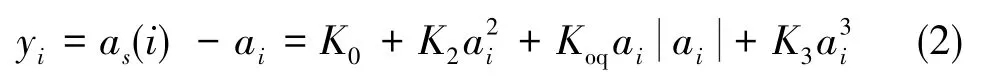
写成矩阵形式有:

其中，A为结构矩阵，K为待求系数矩阵，Y为观测矩阵。

对式（3）使用最小二乘法可以得到误差系数估计式为:

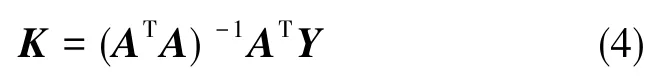
3 显著性分析原理

在进行显著性分析之前，先介绍使用的显著性分析原理［6］。

设想有一组变量y与p（p≥2）个自变量x1，x2，…，xp之间存在相关关系，且满足:

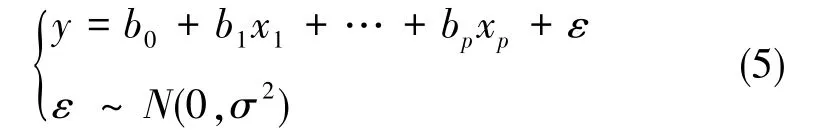
其中，ε为误差项，其分布与（x1，…，xp）的取值无关，在这种多元线性回归模型中，回归系数b=［b1…bp］T的取值不同。

在式（5）中，回归系数b=［b1…bp］T的取值不为零时，称y与（x1，…，xp）之间具有线性依赖关系；相反，当b=0时，则称y与（x1，…，xp）之间没有线性依赖关系。因此这就构成了如下的假设检验问题:

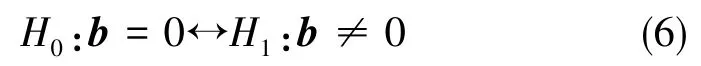
通常称检验问题为相关性检验问题，或称回归方程的显著性检验问题。此外，针对于多元线性回归中某一自变量xi是否对回归关系有贡献，可以提出假设检验问题:

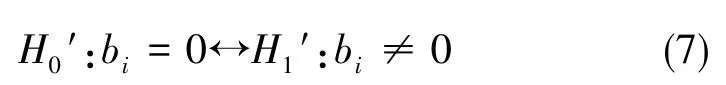
为了利用矩阵工具，记:

并将y和ε写为矩阵形式，则式（5）可以转变为:

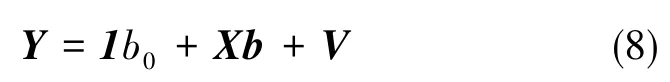
y的总变动平方和:

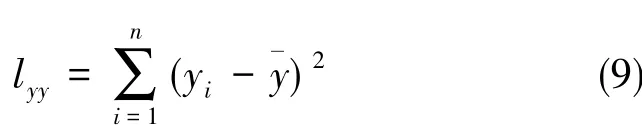
可分解为两部分:

其中，lyy称为总平方和；U称为回归平方和，反映自变量变化时引起的y的波动，它的大小反映了自变量的重要程度；Q称为残差平方和，它是由试验误差和其他未加控制的因素引起的，它的大小反映了试验误差及其他因素对试验结果的影响，U越大，Q越小，则表明y与（x1，…，xp）的线性关系越密切。

在式（5）下，当H0:bi=0为真时，有和且U与Q互相独立，则当H0:bi=0为真时:

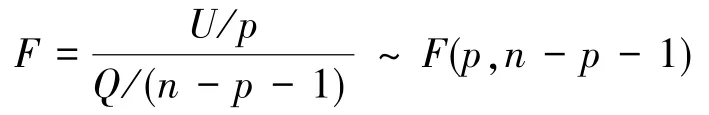
F就是检验假设H0的统计量。因此，对于给定的显著性水平α，由样本观测值计算得F值，若F＞F1-α（p，n-p-1），则拒绝H0，即认为回归效果显著；否则接受H0，即认为回归效果不显著，显著性水平α就是在原假设H0成立的条件下，检验统计量落入否定域内的概率。

当式（8）中矩阵［1 X］的秩为p+1，并且它的误差向量服从零均值的正态分布时，则假设检验问题（式（6））的水平为α的广义似然比否定域由式（11）给出。

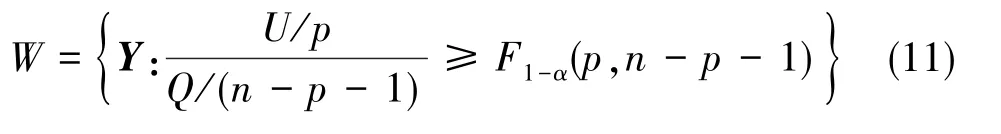
其中，F1-α（p，n-p-1）是自由度为（p，n-p-1）的F分布的1-α分位数。

此外，对于假设检验问题（式（7）），其相应的否定域为:

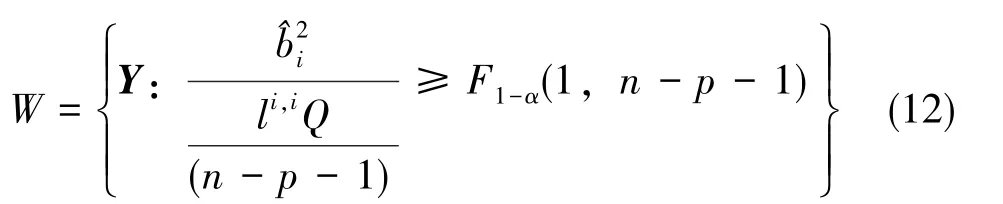
其中，^bi为^b中的第i项，li，i为L-1xx中第i行第i列的值。

4 离心机试验误差系数显著性分析

分别按图2中位置1和位置2对加速度计进行离心机试验，分别采集19个测试点处的加速度计输出，如表1所示。

表1　离心机试验在38个不同加速度输入时的数据Table 1 Output of centrifuge experiment under 38 different accelerations

使用最小二乘方法对表1中的试验数据进行处理，得到各项误差系数如表2所示。

表2　误差系数计算结果Table 2 The results of error separation

对误差模型的显著性进行研究，总变动平方和:

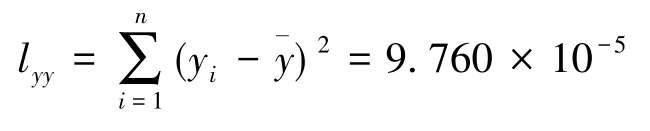
显著性水平定为0.01时，可以计算出:

由以上计算可以看出，对于给定的显著性水平α=0.01，F1-α（p，n-p-1）=F0.99（3，34）= 4.4156，可知F＞F0.99（3，34），拒绝H0，即误差模型建立正确，回归效果特别显著。

对于各误差系数可以得到:

从以上计算可以得出，误差系数K2、Koq、K3均拒绝H0′，即各项系数都是显著的。

回归平方和U可反映所有回归自变量对回归因变量y的总影响。若在所考察的因素中去掉一个因素，回归平方和只会减少，不会增加。减少的数值愈大，说明该因素在回归中起的作用愈大，也就是说该因素愈重要。基于此思想，对K0进行显著性检验。去掉K0后，此时新的偏回归平方和U′反映了其余3个回归自变量所起的作用。计算可得U′=8.274×10-7，Q′=1.290×10-4。

可以看出，对于给定的显著性水平α=0.01，F1-α（p，n-p-1）=F0.99（3，34）=4.4156，可知F＜F0.99（3，34），接受H0，即误差模型建立错误，回归效果不显著。

去除零偏值后误差模型不显著，则误差系数K0是显著的。

从以上计算可以得出，误差系数K0、K2、Koq、K3是显著的，各项误差系数对输出的影响如图3所示。

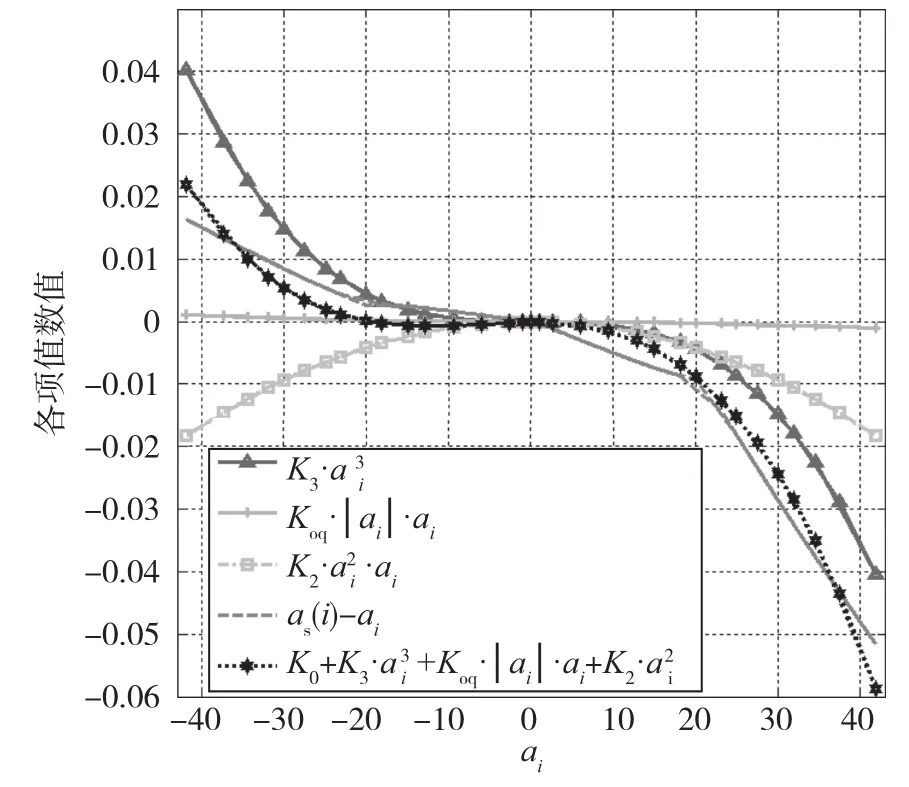
图3　加速度计各项误差系数的影响Fig.3 Influence of QFPA errors

5 结论

本文针对石英加速度计在离心机试验标定过程中误差系数的显著性问题，提出了一套判断误差模型和误差系数的显著性检验方法，验证了加速度计离心机试验中所用模型的正确性，并分别判断了二次项、奇异二次项、三次项及零偏值的显著性。

由于所使用的显著性分析方法原理具有通用性，也可将其运用于其他误差分离试验，保证最终的误差模型的正确性及误差系数分离可靠。

［1］IEEErecommendedpracticeforprecisioncentrifuge testing of linear accelerometers［S］.IEEE Std 836-2009.

［2］IEEE recommended practice for inertial sensor test equipment，instrumentation，data acquisition，and analysis［S］. IEEE Std 1554-2005.

［3］乔永辉，刘雨，苏宝库.陀螺加速度计二次项系数K2的离心机测试方法研究［J］.中国惯性技术学报，2007，15（1）:120-122. QIAO Yong-hui，LIU Yu，SU Bao-ku.Testing methodology for second-order coefficient K2of gyro accelerometer by centrifuge［J］.Journal of Chinese Inertial Technology，2007，15（1）:120-122.

［4］乔仁晓，孟晓风，季宏.加速度计非线性项系数校准误差分析与建模［J］.系统仿真学报，2008，20（6）: 1633-1635. QIAO Ren-xiao，MENG Xiao-feng，JI Hong.Error analysis and modeling in calibration of accelerometers'nonlinear terms'coefficients［J］.Journal of System Simulation，2008，20（6）:1633-1635.

［5］邢海峰，任顺清，祁家毅，等.加速度计二次奇异项系数的形成机理与标定方法［J］.航天控制，2009，27（2）:91-95. XING Hai-feng，REN Shun-qin，QI Jia-yi，et al.The mechanism and calibrating method of accelerometer［J］. Aerospace Control，2009，27（2）:91-95.

［6］刘建波，魏宗康.石英加速度计误差系数显著性分析［J］.中国惯性技术学报，2011，19（5）:615-617. LIU Jian-bo，WEI Zong-kang.Significance analysis of QFPA's error model's coefficients［J］.Journal of Chinese Inertial Technology，2011，19（5）:615-617.

Significance Analysis of QFPA's Coefficients Based on Centrifuge Experiment

HUANG Chao，WEI Zong-kang，HU Rong-hui
（Beijing Institute of Aerospace Control Devices，Beijing 100039）

Some coefficients of the QFPA's error model could be trustless because of the test technique's limit.Therefore，it's necessary to analyze the result and reject the unauthentic coefficients and simplify the error model.A method is put forward to solve this problem based on centrifuge experiment which is one of the error separation tests and taking QFPA as our test object.In this method，F-distribution is taken as the statistics to verify the hypothesis，and an detailed test's analysis is carried out.As its generality，this method can also be applied to other kinds of methods.

accelerometer；significance analysis；parameters identification；centrifuge experiment

U666.1

A

1674-5558（2016）05-01126

10.3969/j.issn.1674-5558.2016.05.017

黄超，男，导航制导与控制专业，硕士，研究方向为捷联惯性技术。

2015-06-01