基于自适应鲁棒反演的固体动能拦截器姿态跟踪控制

杨　旭，姚晓先，张　皎，刘源翔

(北京理工大学 宇航学院，北京　100081)



基于自适应鲁棒反演的固体动能拦截器姿态跟踪控制

杨旭，姚晓先，张皎，刘源翔

(北京理工大学 宇航学院，北京100081)

针对固体动能拦截器姿控发动机推力恒定、分散式布局控制力矩的强耦合特性及系统模型存在不确定特点的拦截器姿态稳定跟踪控制问题，提出了一种基于自适应鲁棒反演的新型姿态控制器设计方法。充分考虑姿态控制系统中三通道及姿控推力间的相互耦合关系，建立了姿态控制耦合模型，利用反演及滑模方法设计了实际与虚拟控制量。通过自适应方法对系统内各通道间的耦合及不确定项进行估计及补偿，提高了姿态控制的精度。基于PWPF调制方法，将设计的连续控制量解算成可直接用于姿态控制的脉冲控制量，实现了拦截器的数字变推力控制。仿真结果表明，所设计的姿态控制算法在参数摄动及存在不确定干扰的情况下，仍满足姿态稳定跟踪要求。

动能拦截器；变推力控制；PWPF调制器；不确定性

0　引言

动能拦截器(Kinetic Kill Vehicle)作为一种大气层外超高速飞行器，利用其高速飞行产生的巨大动能，通过直接碰撞摧毁来袭目标[1]。与传统大气层内制导武器利用空气动力改变自身姿态不同，动能拦截器通过姿态控制系统(Attitude Control System)中的姿控发动机产生矢量推力改变弹体姿态。拦截器进入末制导阶段时，为了搜索目标其姿态，经常需要大角度调整[2]，定位目标后，则需根据不同的拦截策略[3-4]，控制拦截器的姿态角跟踪弹目视线角，实现以“零控脱靶量”为目标的精确拦截。因此，拦截器姿态的精准控制对实现成功命中至关重要。

针对动能拦截器的姿态控制问题，国内外学者提出了多种控制器设计方法[5-9]。Philip C等[5]利用相平面法，设计了用于拦截器姿态稳定的控制器。Tobin C等[6]针对几种常用的脉冲调制方法，利用描述函数法设计了稳定的控制器，但这种近似设计方法控制的姿态角精度不高，且稳态抖动较大。杨宝庆等[7]利用预测控制理论，设计了一种开关式姿态控制律。该方法在建模中考虑姿态控制各通道存在干扰力矩及推力偏心的情况，将系统模型近似为线性模型，并设计了预测控制器，取得了不错的效果，但该方法需要拦截器的转动惯量实时可测，不利于工程实现。支强等[8]基于时标分离原理，设计了一种比例积分控制器。该方法将姿态控制系统分为快慢回路，并设计了相应的控制律，实现了对拦截器的姿态控制，但该设计方法中并未讨论参数摄动及外部扰动对控制系统的影响。Xu Xingyuan等[9]基于线性二次型最优控制理论，设计了一种拦截器姿态控制律。该方法的核心是忽略系统中的耦合部分，从而将非线性耦合系统转化为线性三通道独立系统，并利用最优函数设计对应通道的控制律。目前，相关文献所设计的姿态控制律多是在忽略姿控发动机具体布局形式的前提下，将各通道间的耦合项视为小量忽略，进而实现对三通道独立设计。但这种设计方法需要建立在拦截器滚转角及姿态角速率不大，且三通道控制力矩相互独立的前提下。在动能拦截器的实际应用中，由于姿控发动机的布局形式不同，从而使各通道间存在较严重的耦合，难以分通道独立设计。同时，由于需要抑制各通道之间的耦合关系，使系统控制律设计更加保守，不利于系统整体性能的提高。综上所述，需要更多对动能拦截器一体化姿态控制方法的研究。

动能拦截器的姿态控制系统是具有强耦合及多输入多输出的强非线性系统，在其控制过程中，主要存在两类不确定因素：一是空间环境带来的外部扰动；二是转动惯量建模不确定、推力偏心及质心漂移等内部扰动，这也对控制器的设计提出了更高的要求。自适应控制是一种在系统存在某种不确定的情况下，依然能够保持控制性能的控制算法[10]，广泛用于飞行器的姿态控制[11-14]中。由于许多利用非线性控制理论设计的控制器得到的是时变连续控制量，并不能直接用于动能拦截器的姿态控制中。针对这一问题，许多学者提出了连续控制指令的脉冲调制方式，如脉冲宽度调制(PWM)，脉冲频率调制(PFM)，脉宽脉频调制(PWPF)等不同方式[15-17]。其中，PWPF调制方式以其良好的性能广泛用于飞行器的姿态控制领域。Krovel T[15]提出了PWPF调制器的参数选择原则及参数选择建议范围。Navabi等[16]针对飞行器姿态控制问题，分别从近似线性区间、燃料消耗、发动机工作频率等方面，讨论了PWPF调制器的性能。在实际应用中，还需要结合拦截器姿态发动机布局形式具体分析，对于不同的布局形式，各通道控制力产生的控制力矩耦合情况不同，需在控制算法中予以考虑。

针对动能拦截器姿态控制系统中存在强耦合及不确定性的问题，本文利用自适应技术对姿态控制系统中存在的不确定和扰动的上界进行估计和补偿，使设计的鲁棒反演控制律在无需获得控制过程中的转动惯量变化、质心漂移和外部扰动等信息的前提下，完成对姿态的跟踪控制，扩大了控制律的应用范围。通过PWPF调制器，将所设计的连续控制律转化为适用于动能拦截器的脉冲控制律，使拦截器能够快速跟踪期望指令，并保持稳定。

1　动能拦截器三通道耦合建模

动能拦截器无舵无翼，其姿态的调整仅依靠安装在弹体后部的姿态控制系统实现。姿态控制系统主要有四发动机布局方案、六发动机布局方案、八发动机布局方案等[18]。由于六发动机分散式布局方案兼顾控制精度与结构设计简便，本文以其为研究对象，具体姿控发动机布局如图1所示。其中，发动机1#、4#控制拦截器的俯仰运动，发动机2#、3#、5#、6#控制拦截器的滚转及偏航运动。分析可知，姿态控制力矩在滚转和偏航通道存在耦合。

动能拦截器由于体积较小，且外形多为轴对称，一般可将弹体作为刚体研究，并认为弹体坐标系为其惯性主轴系[7]。由此拦截器对弹体坐标系各轴的惯性积为零，则描述拦截器绕质心转动的运动学和动力学方程为

(1)

式中ϑ、ψ、γ分别为拦截器的俯仰角、偏航角、滚转角；Jx、Jy、Jz分别为拦截器相对于弹体坐标系3轴的转动惯量；ωx、ωy、ωz分别为弹体坐标系相对于惯性系的转动角速度在弹体坐标系3轴上的分量；F1、F2、F3分别为2#、6#号，3#、5#号，1#、4#号发动机作用于拦截器的推力；lr为滚转控制力矩的推力矢量作用距离；ld为俯仰、偏航控制力矩的推力矢量作用距离；dx、dy、dz分别为外界扰动及推力偏心产生的干扰力矩在弹体坐标系3轴上的分量。

图1　动能拦截器姿控发动机布局示意图

取系统的状态变量X1=[ϑψγ]T，X2=[ωzωyωz]T，整理式(1)有

(2)

其中

其中，参数矩阵L表示六姿控发动机分散式布局方案的控制力矩耦合形式。由于拦截器在姿态调整时，需要开启发动机提供推力，并消耗燃料，而这会导致拦截器自身转动惯量的变化及质心漂移，故式(2)中的参数矩阵存在下述关系：

(3)

式中J0、F0、L0分别表示参数矩阵J、F、L的初始值;ΔJ、ΔF、ΔL分别表示由转动惯量变化及质心漂移产生的各参数的变化量。

假设1：干扰力矩D(t)未知有界，即|di(t)|≤gi，gi为正实数，且i=x,y,z。

假设2：拦截器转动惯量Ji=Ji,0+ΔJi，Ji,0为已知初始惯量，ΔJi为转动惯量的不确定有界变化量，满足|ΔJi|≤Jδi，Jδi为正实数，且i=x,y,z。

假设3：姿态控制力矩的推力矢量作用距离li=li,0+Δli，li,0为已知初始作用距离，Δli为作用距离的不确定有界变化量，满足|Δli|≤lθi，lθi为正实数，且i=r,d。

由假设2、假设3及式(2)、式(3)整理拦截器动力学方程有

(4)

式(4)表示为矩阵形式有

(5)

(6)

联立式(2)、式(6)得系统的状态方程：

(7)

其中

(8)

可看出，新变量H(t)为系统总不确定项，包含外界扰动、转动惯量摄动、质心漂移等未知不确定信息。

2　动能拦截器姿态控制器设计

由式(7)可知，上述系统为带有不确定项的时变非线性系统。反演设计方法，是解决不确定非线性系统的有效方法，下面基于反演设计思想，提出一种自适应滑模控制算法，来解决系统(7)在假设1～假设3约束下的输出调节问题。

假设4：系统(7)中的各状态量均可测，且其变化量均有界。

(9)

内取值时，矩阵G可逆。

证明：经计算矩阵G的行列式

是关于ϑ的连续函数，故根据连续函数性质可知，对任意的|ϑ|≤ϑmax，其中ϑmax<π/2为正实数，存在正实数ψmax<π/2，γmax<π/2，使得当|ψ|≤ψmax，|γ|≤γmax时，det(G)=-1/cosϑ<0，即矩阵G可逆。证毕。

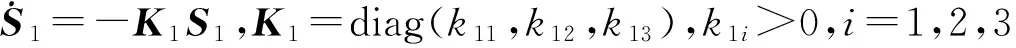
(10)

X2d可通过时间常数τi>0，i=1,2,3的低通滤波器计算得到

(11)

其中，τ=diag(τ1,τ2,τ3)，定义系统的滑模面S2=[S21S22S23]T=X2-X2d，为了能够在有限时间快速到达滑模面，选择趋近律：

(12)

其中

将式(12)代入式(8)，可得系统的控制量：

(13)

由式(13)可看出，未知总扰动H(t)出现在控制量的表达式中。自适应控制技术广泛用于处理系统中存在不确定项的问题，通过对未知项上界的估计，将估计值引入控制量中补偿未知项，可达到改善控制器性能的目的。

假设5：动能拦截器的姿态控制力u有界，且满足

(14)

式中‖Xξ‖=‖X1‖+‖X2‖；c0、b0为未知常数，且满足c0≥0，b0≥0。

假设 6：系统的总扰动H(t)有界，且满足

(15)

式中c≥c0，b≥b0为未知有界参数。

定义如下自适应律[12,19]：

(16)

更新律：

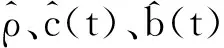
将式(16)代入式(13)，有闭环系统的控制量：

(17)

注释1：在假设4的条件下，由控制量式(17)可知，该算法不需要拦截器转动惯量变化、推力偏心及外部扰动的任何信息，仅需要已知拦截器初始惯量值及初始质心位置，即可实现对拦截器的姿态控制，这些量均可在地面测试获得。甚至在初始惯量及初始质心位置未知的情况下，通过在控制器中设计合理的参数J0、L0，也同样可实现对拦截器姿态的有效控制。

3　稳定性分析

定义低通滤波器解算误差：

(18)

以及估计误差：

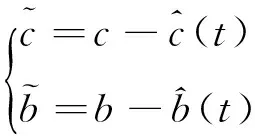
(19)

对式(18)和式(19)分别求导，有

(20)

由定义的滑模面S1、S2，可知

(21)

由关系式(21)，可计算出滑模面的动态形式:

(22)

针对闭环系统(8)，构造如下Lyapunov函数：

V=V1+V2+V3

(23)

其中

(24)

(25)

(26)

显然，对于任意的t(t≥0)，有V>0，对式(24)、式(25)、式(26)分别求导，可得

(27)

式中k1 min为正定对角阵K1对角元素的最小值。

(28)

式中k2 min为正定对角阵K2对角元素的最小值。

式(29)中，τmax为低通滤波器时间常数矩阵τ中对角元素的最大值。

(29)

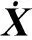
其中，φ1、φ2分别为非负连续函数，其在定义域内存在的最大值分别记为N、M(M的大小由参数K1确定)。

综上所述，联立式(27)～式(29)，可得：

(30)

其中

(31)

如果设计参数满足

(32)

其中，κ为一正数，则有

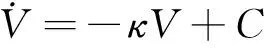
(33)

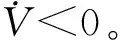
(34)

注释2：为了加快S1、S2的收敛速度，可通过增大参数Ki(i=1,2)、σ及减小参数τ的方法实现。但在工程应用中，低通滤波器时间常数τ的选择不可能任意小，且过大的参数Ki、σ会使系统的超调增大，不利于拦截器的姿态稳定。因此，对于控制器的参数选取，需兼顾滑模收敛的快速性及姿态控制的稳定性。

4　基于PWPF的姿态控制律设计

动能拦截器姿态控制系统采用常值推力发动机，其推力输出形式：

(35)

式中uc为推力发动机控制信号；W为发动机的推力常值；F为发动机推力输出。

由于式(17)设计的控制量为连续形式，无法直接用于驱动姿态控制发动机，达到调节姿态的目的，故需将其转化为脉冲形式。本文利用由一阶滤波器及施密特触发器(Schmitt trigger)组成的PWPF调制器对连续控制律进行调制，以实现数字变推力的目的，其工作原理[14]如图(2)所示。

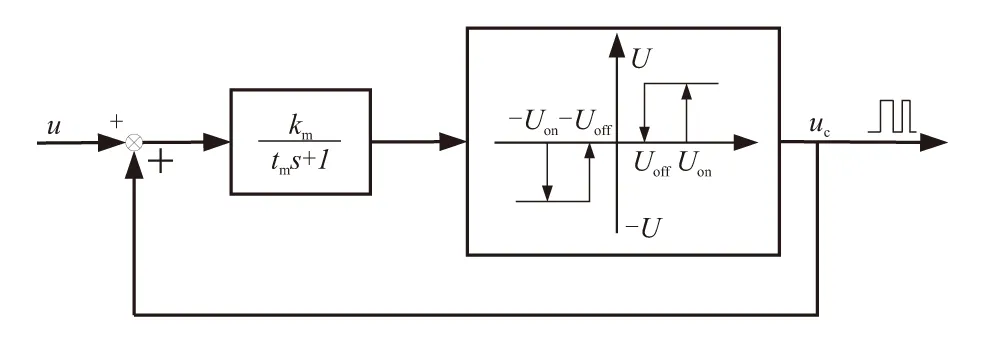
图2　PWPF调制器原理框图

图2中，u为连续控制力指令；km和tm分别为一阶滤波器的增益和时间常数；Uon和Uoff分别为施密特触发器的启动和关闭阈值；uc为调制器脉冲输出。PWPF调制器通过对比需求控制指令u与调制器输出uc的工作状态，根据差异驱动调制器改变推力状态，并通过设计参数可调的一阶滤波器及施密特触发器产生脉宽可变的控制信号。

定义PWPF调节器的迟滞h=Uon-Uoff，则其最小工作时间tmin为[14]

(36)

注释4：在实际设计中，调节器的参数选择需考虑多种实际因素。发动机工作的频率需避开拦截器弹体的固有频率，以免产生共振，且工作频率不宜过高，否则会增加系统的硬件实现难度。控制信号的最小脉冲宽度需大于发动机推力矢量的切换时间及发动机最小工作时间，由式(36)可知，需通过调节参数h、tm、km的大小，以满足实际需求。选择小的时间常数tm，可增加系统的响应速度降低延迟，调节滤波器增益km，可增大系统线性区间。虽然较小的时间常数及较大的增益会获得更高的调节精度，但这样会增加发动机的开启次数及切换频率，并增加燃料消耗，故具体参数的选择，需要对上述因素综合考虑。

5　仿真结果及分析

为验证本文设计的基于自适应鲁棒反演的姿态控制律的有效性，以某动能拦截器为控制对象，针对不同的跟踪控制指令信号进行非线性数值仿真。

定义动能拦截器末制导阶段各参数的初始值及参数变化见表1、表2。

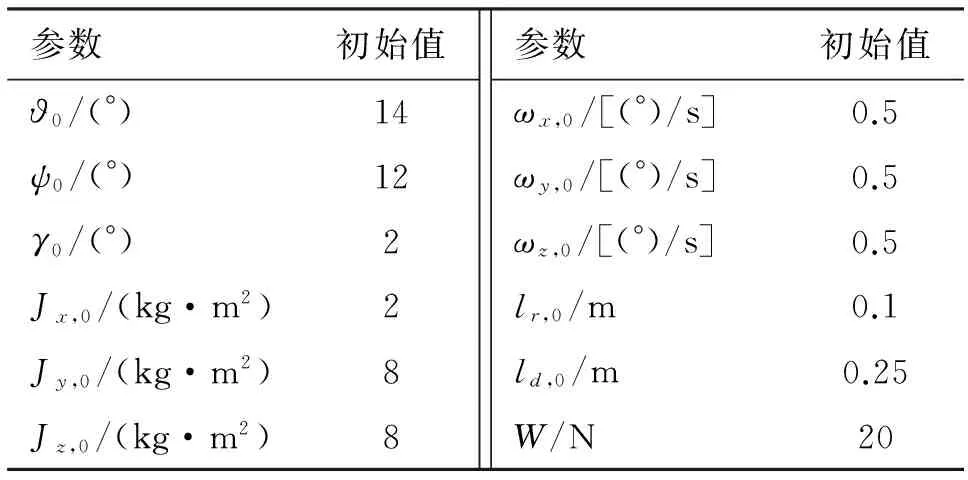
表1　仿真参数初始值

表2　仿真参数变化值

本文所述的控制律参数分别为滑模矢量矩阵参数K1=diag(3.5,3.5,3.5)，K2=diag(6,6,6)；σ=diag(10,10,10)，νi=0.8,i=1,2,3；低通滤波器时间常数矩阵τ=diag(0.2,0.2,0.2)；自适应律参数ε1=0.6，ε2=0.6，p1=1，p2=1；PWPF调制器参数km=3，tm=0.2，Uon=0.19，Uoff=0.02。

同时，为保证动能拦截器在末制导的过程中飞行姿态稳定，限定角速度‖ω‖≤5(°)/s；考虑实际拦截器的姿态控制发动机存在响应延迟，这里假设其动态特性近似时间常数为0.01的一阶惯性环节，表达式为

(35)

为体现所提出设计方法的有效性，将其与基于线性二次型最优控制理论(LQR)设计的三通道独立解耦姿态控制算法[9]进行对比分析。该设计方法的核心是忽略系统中的耦合项，将系统模型简化为三通道独立的线性模型，利用最优函数分通道独立设计各自的控制器。本文取与文献[9]中相同的最优函数，经计算可得控制器参数如下

(36)

式中Mx、My、Mz分别为作用在拦截器弹体系3个轴上的控制力矩。

为方便表达，以“ADSM”表示基于自适应鲁棒反演的拦截器姿态控制算法，以“LQR”表示基于LQR的最优姿态控制算法。下面以跟踪姿态角阶跃指令为目标，分别对比2种算法，如图3～图5所示。

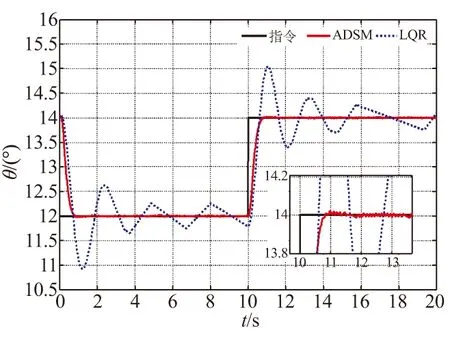
图3　动能拦截器俯仰角响应曲线

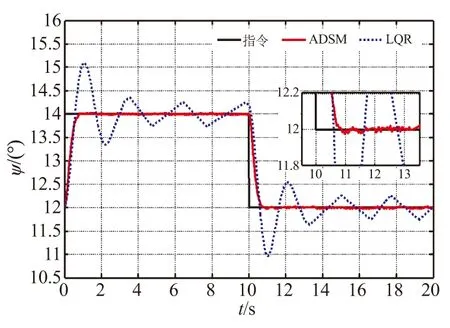
图4　动能拦截器偏航角响应曲线

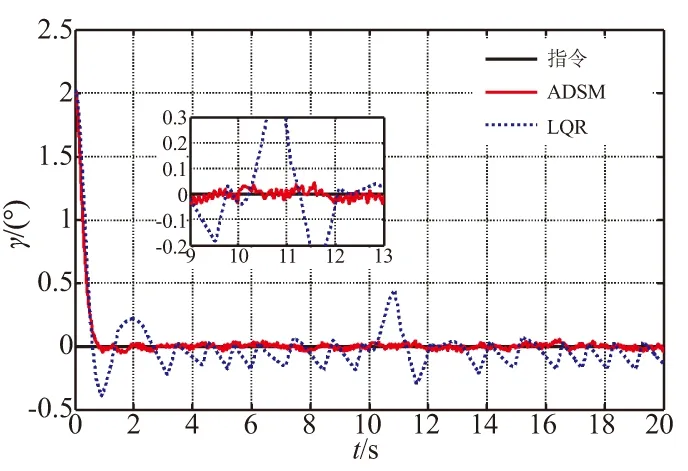
图5　动能拦截器滚转角响应曲线

由上述仿真结果可知，与基于线性二次型最优控制理论设计的控制律相比，本文设计的自适应鲁棒反演控制律，可提供更快的收敛速度以及更高的收敛精度。

图3为动能拦截器在2种控制律的作用下，跟踪阶跃俯仰角指令的响应曲线。由仿真结果可知，控制律ADSM在跟踪阶跃跳变指令时，需经过约0.8 s的调整过程完成姿态跟踪。在姿态稳定控制时，俯仰角误差较小，并保持在±0.01°以内。控制律LQR的超调量较大，在稳定控制时，俯仰角误差在±0.3°左右，误差较大。

图4、图5分别为拦截器在2种控制律的作用下，跟踪阶跃偏航角及滚转角指令的动态响应曲线。由仿真结果可知，控制律ADSM在偏航、滚转通道，经约0.8 s完成姿态指令跟踪，并保持±0.01°的稳态姿态角误差。控制律LQR在两通道的超调量较大，稳态姿态角误差约为±0.3°。从图5可看出，控制律LQR在10～12 s时滚转角的抖动很大。这是由于俯仰、偏航角的控制指令改变，三通道独立解耦所忽略的小量增大，在动能拦截器三通道间的强耦合作用下，导致滚转角大幅抖动。而控制律ADSM由于采用了三通道一体化设计方法，在姿态控制指令改变时，滚转角控制效果并没有明显变化。

图6为控制律ADSM对姿控发动机的控制指令。由图6可知，由于外部扰动、推力偏心及控制力矩在偏航滚转通道耦合等因素，姿控发动机需频繁开启，以保持姿态的快速跟踪及稳定。对于姿态控制，发动机开启频率的增大，有利于提高姿态控制的精度，但将增加燃料消耗，在工程应用中，需综合考虑控制精度与能源的经济性。

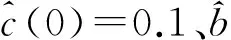
由上述分析可知，自适应律(16)能够有效地估计总扰动的上界，并通过在控制律中的有效补偿，提高了系统的控制精度。

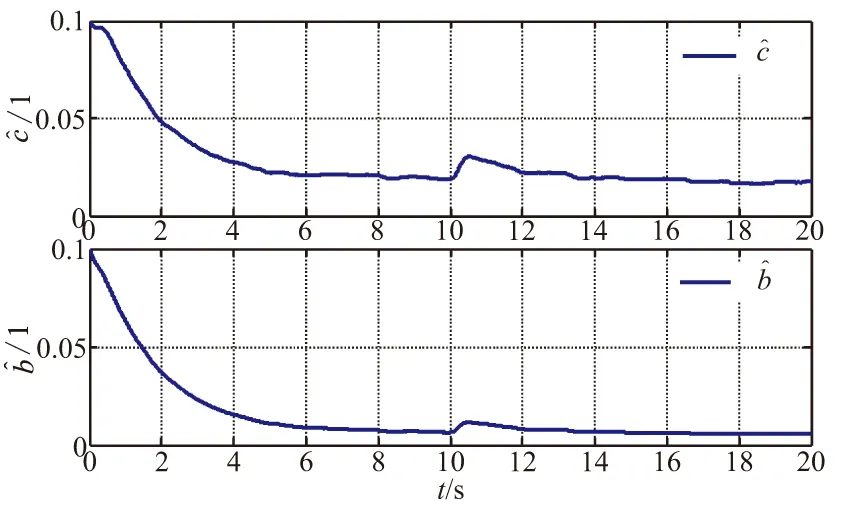
图7　自适应参和的估计值

6　结论

针对固体动能拦截器姿态快速跟踪稳定控制问题，在考虑姿控发动机布局形式及推力恒定的情况下，本文设计了一种基于自适应鲁棒反演的一体化姿态控制算法。

(1)在转动惯量变化及外部扰动信息未知的条件下，通过估计各通道间耦合及总扰动的上界，对控制量中的不确定项予以补偿，使得拦截器的姿态角平稳变化，并快速收敛。

(2)与基于LQR的传统三通道独立设计方法相比，同时考虑在拦截器转动惯量变化、质心漂移及存在外部扰动的情况下，本文给出的姿态控制算法跟踪精度更高、收敛速度更快，抗扰能力更强，进一步验证了该方法的有效性及优越性。

(3)利用PWPF调制器，将连续控制量解算为适用于动能拦截器姿态控制的脉冲控制量，实现了数字变推力控制，使之具有更好的工程应用前景。

[1]朱战霞,韩沛,陈鹏.基于非线性Terminal滑模的动能拦截器末制导律设计[J].西北工业大学学报,2013,31(2): 233-238.

[2]王庆超,李达.基于反馈线性化的动能拦截器姿态控制研究[J].宇航学报,2005,26(3):358-361.

[3]Zhou D,Sun S,Teo K L.Guidance laws with finite time convergence[J]. Journal of Guidance,Control,and Dynamics,2009,32(6):1838-1846.

[4]杨旭,张皎,刘源翔.基于碰撞航线的动能拦截器滑模制导律设计[J].北京航空航天大学学报,2014,40(9):1000-1005.

[5]Philip C Calhoun, Eric M Queen. Entry vehicle control system design for the Mars science laboratory[J]. Journal of Spacecraft and Rockets,2006,43(2):324-329.

[6]Tobin C Anthony, Bong Wie. Pulse-modulate control synthesis for a flexible spacecraft[J]. J. Guidance,1989,13(6):1014-1022.

[7]杨宝庆,姚郁,贺风华.大气层外拦截器开关式姿态控制律设计[J].哈尔滨工业大学学,2010,42(1):5-8.

[8]支强,蔡远利.动能杀伤器侧窗定向机制分析及建模[J].西安交通大学学报,2012,46(1):91-96.

[9]Xu X, Cai Y. Pulse-width pulse-frequency based optimal controller design for kinetic kill vehicle attitude tracking control[J].Applied Mathematics,2011(2):565-574.

[10]Polycarpou M M, Ioannou P A. A robust adaptive nonlinear control design[J]. Automatica,1996,32(4):423-427.

[11]Ran M, Wang Q, Hou D, et al. Backstepping design of missile guidance and control based on adaptive fuzzy sliding mode control[J]. Chinese Journal of Aeronautics, 2014,27(3):634-642.

[12]Zhu Z, Xia Y, Fu M. Attitude stabilization of rigid spacecraft with finite-time convergence[J]. International Journal of Robust and Nonlinear Control,2011,21(6):686-702.

[13]Xia Y, Zhu Z, Fu M, et al. Attitude tracking of rigid spacecraft with bounded disturbances[J]. IEEE Transactions on Industrial Electronics,2011,58(2):647-659.

[14]Hou M, Liang X, Duan G. Adaptive block dynamic surface control for integrated missile guidance and autopilot[J]. Chinese Journal of Aeronautics.2013,26(3):741-750.

[15]Krovel T D. Optimal tuning of PWPF modulator for attitude control[D]. Trondheim,Norway:Norway University of Science and Technology,2005.

[16]Navabi M, Rangraz H. Comparing optimum operation of pulse width-pulse frequency and pseudo-rate modulators in spacecraft attitude control subsystem employing thruster[C]. Proceedings of 6th International Conference on Recent Advances in Space Technologies,2013:625-630.

[17]Hu Q, Ma G. Flexible spacecraft vibration suppression using PWPF modulated input component command and sliding mode control[J]. Asian Journal of Control,2007, 9(1):20-29.

[18]石凯宇,程英容,张奕群.姿控发动机布局方式研究[J].现代防御技术,2012,40(2):44-49.

[19]Andrievskii B R, Fradkov A L. Method of passification in adaptive control,estimation,and synchronization[J]. Automation and Remote Control, 2006, 67(11):1699-1731.

[20]Khail H. Nonlinear system[M]. New Jersey: Prentice Hall,1996.

(编辑：薛永利)

Attitude tracking of KKV based on adaptive backstepping sliding mode control

YANG Xu, YAO Xiao-xian, ZHANG Jiao, LIU Yuan-xiang

(School of Aerospace Engineering, Beijing Institute of Technology, Beijing100081, China)

Aiming at the problem of exo-atmospheric kinetic kill vehicle (KKV) attitude tracking with the characters of constant thrust, nonlinearity, strong couplings and parameter uncertainties, a novel sliding mode controller was designed which is based on adaptive backstepping theory. The attitude coupling mode was established which considered about interaction between three channels and control torque in control loop. The actual control laws and virtual control laws were derived based on the design procedures of sliding mode control and backstepping control, respectively. An adaptive method was introduced to estimate and compensate the model couplings and uncertainties, which improved the accuracy of altitude control. The pulse control laws which could be used for attitude control directly, were calculated from the continuous laws with PWPF modulation. The simulation results show that attitude tracking still satisfies requirements with parameters and disturbance uncertainties.

kinetic kill vehicle；thrust variable control；PWPF modulator；uncertainty

2015-08-26；

2015-11-19。

国家高技术研究发展计划资助项目；国家“985”工程三期重点建设项目。

杨旭(1986—)，男，博士生，研究方向为飞行器动力学与控制。E-mail:yangxu@bit.edu.cn

V423

A

1006-2793(2016)05-0715-08

10.7673/j.issn.1006-2793.2016.05.021