带有攻角约束的高超声速飞行器航迹倾角跟踪控制方法
2016-11-03王易南符文星
王易南,陈 康,符文星,闫 杰
(西北工业大学 航天学院,西安 710072)
带有攻角约束的高超声速飞行器航迹倾角跟踪控制方法
王易南,陈康,符文星,闫杰
(西北工业大学 航天学院,西安710072)
针对高超声速飞行器高速飞行过程中受攻角的限制的控制问题,研究了一种基于障碍Lyapunov函数的状态约束航迹倾角跟踪控制方法。首先对飞行器航迹倾角模型进行部分线性化,得到符合严反馈的条件的参数化方程。采用BLF反步法,设计了对攻角具有约束的航迹倾角跟踪控制器,证明了控制器的稳定性并给出攻角响应范围和控制器参数的关系。仿真中使用反步法和BLF方法进行对比。结果表明,采用BLF方法设计的控制能在满足高超声速飞行器攻角约束条件下,实现对飞行器航迹倾角的无差跟踪。
攻角约束控制;倾角跟踪;障碍李雅普洛夫函数;反步法
0 引言
以超燃冲压发动机及综合推进系统为动力的高超声速飞行器,能够在大气层内以Ma>5的速度飞行,在军事和民用两方面都有重要的应用价值,是未来航空航天领域主要的发展方向。美国X-43的试飞成功,表明超燃冲压发动机技术取得了突破性进展。超燃冲压发动机正常工作时,需要进气道能捕获足够的空气,而进气道捕获空气的能力与飞行器的攻角密切相关,需要飞行器保证攻角在±4°以内,否则会导致超燃冲压发动机关机[1],从而也对飞行器的控制系统提出了更高要求。
高超声速飞行器在飞行时满足攻角范围要求,本质上是一个具有状态不等式约束的非线性控制问题。目前,解决带有状态约束控制问题的主要有参考轨迹调节器[2-3]、模型预测控制[4]、基于不变集原理[5]的控制器设计和极值搜索控制[6-7]。这些方法本质上均基于数值方法,且计算较复杂。此外,障碍Lyapunov函数(Barrier Lyapunov Function,BLF)法也是解决具有约束条件控制问题的有效方法。Neo最早提出这种方法,在反步法中构造BLF,解决了具有Brunovsky标准型的状态约束控制[8]。而后Tee等基于Neo的思想,把BLF推广到非线性领域,并做了更详尽研究。Tee将BLF方法与自适应控制结合,构造了对称与非对称BLF,解决了带有参数不确定性反馈非线性控制系统的输出约束、全状态约束和部分状态约束的控制问题[9-12]。
飞行器控制中,航迹倾角跟踪控制是实现飞行器高度控制的一种有效方法,本文针对以超然冲压发动机为推进系统的高超声速飞行器模型,设计具有攻角约束的倾角跟踪控制系统。首先对航迹倾角控制系统,通过忽略高超声速飞行器气动力函数中关于小状态量的高阶项,把系统模型的化为严反馈形式。通过构造BLF函数、反正切函数和反步法,设计了带有攻角误差状态约束的控制器,结合带有饱和限制的指令滤波器,实现了在攻角约束条件下的航迹倾角指令跟踪。对控制器的稳定性进行了分析,同时给出了攻角约束界限与控制器参数的关系。最后通过仿真验证,说明了控制器的有效性。
1 高超声速飞行器纵向模型
高超声速飞行器的纵向动力学模型[13]可由下列方程描述:
(1)
(2)
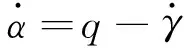
(3)
(4)

(5)
式中v、γ、α、q和h为方程状态变量,分别表示速度、航迹倾角、攻角、俯仰角速度和高度;T、D、L和Myy为发动机推力、阻力、升力和俯仰力矩;Iyy为飞行器转动惯量;m为飞行器质量。
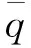
假设1:在高超声飞行器高度控制中,飞行器的速度近似为常数,且速度大小的变化率近似为零。
假设2:飞行器的攻角α很小,做近似sinα≈α,且在气动力和气动力矩系数中忽略与α高次项有关的系数。
在假设1和假设2的条件下得到高超声速飞行器航迹倾角反馈参数控制模型:
(6)
(7)
(8)
其中
2 攻角受限条件下航迹倾角跟踪
2.1带有攻角限制的航迹倾角跟踪控制器设计
Step 1:定义对倾角跟踪误差信号,并对其求导:
(9)
设计Lyapunov函数,并对Lyapunov函数求导:
(10)
定义攻角误差信号:
(11)
式中u1为虚拟控制输入。
设计u1:
(12)
式中c1为控制器参数。
(13)
通常在反步法设计控制器时,把虚拟控制u1设计成如下形式:
(14)
得到具有二次形式的Lyapunov函数的导数:
(15)
由于本文目的是设计攻角约束条件下的控制器,从攻角误差的定义中可得到α=e2+u1,攻角的边界是与虚拟控制输入u1有关,如果使用式(14)作为虚拟输入,|u1|的边界很难计算,所以在这使用有界的反正切函数设计虚拟控制输入u1。
Step 2:设计对攻角误差具有限制作用的Lyapunov函数:
(16)
式中kb为函数的参数,用于限制误差的变化范围。
定义俯仰角速度误差e3:
e3=q-u2
(17)
式中u2为虚拟控制输入,用于镇定状态α。
设计u2:
(18)
式中c2为控制器参数。
(19)
Step 3:设计Lyapunov函数V3:
(20)
设计控制器输入:
(21)
把δ代入设计Lyapunov函数V3的导数,得
(22)
由此得到高超声速飞行器攻角限制下的倾角跟踪控制系统闭环控制器:
(23)
相对应的Lyapunov函数和其导数:
(24)
(25)
2.2稳定性分析
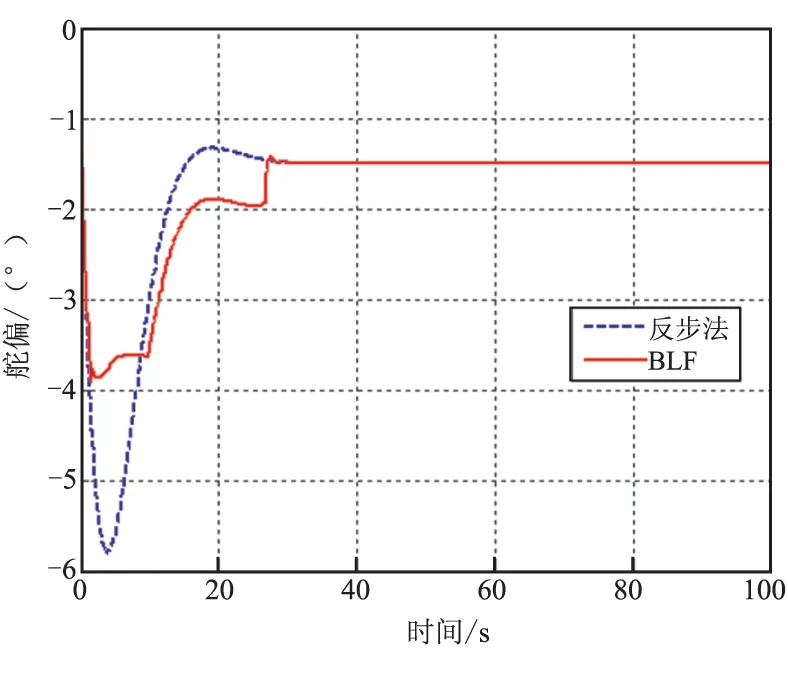
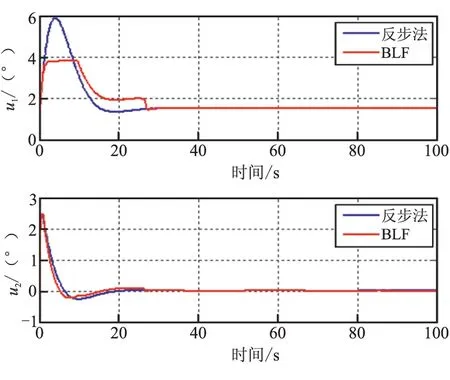
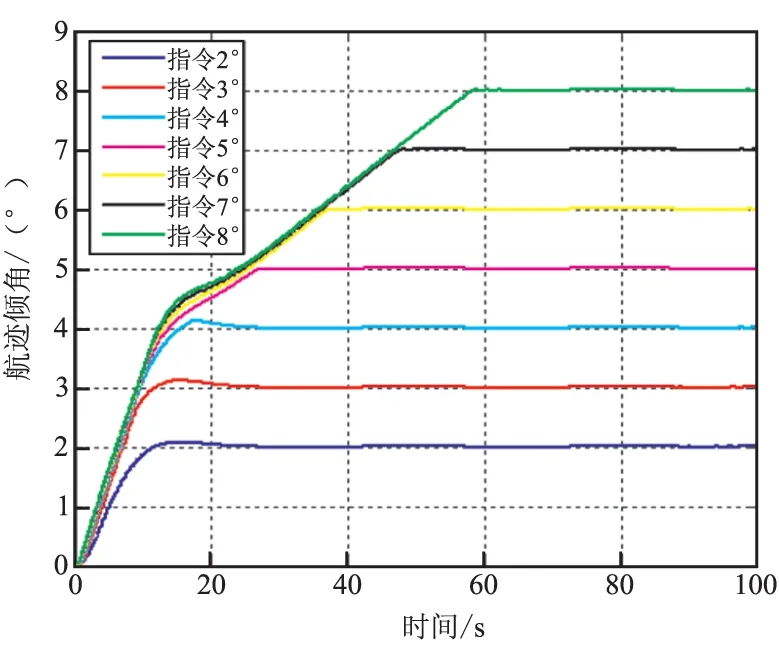
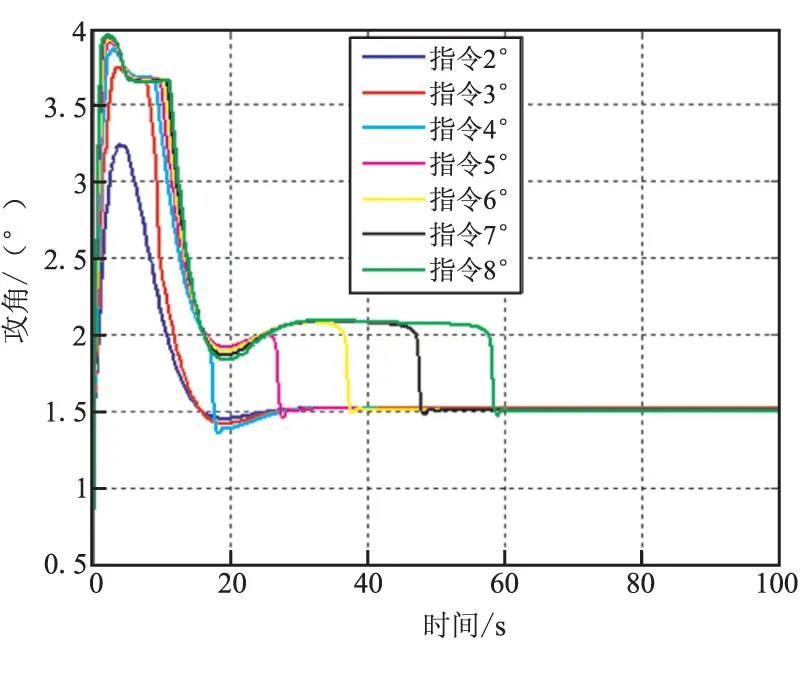
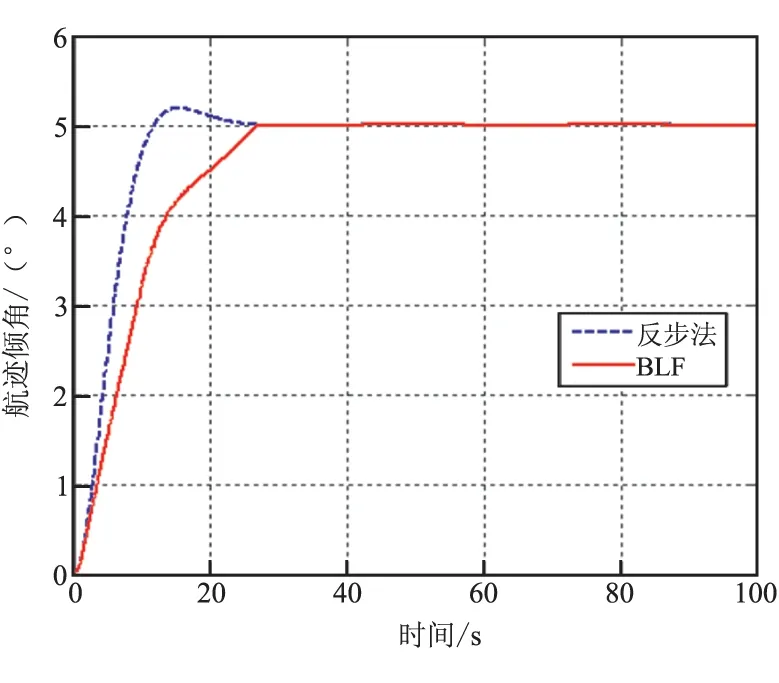
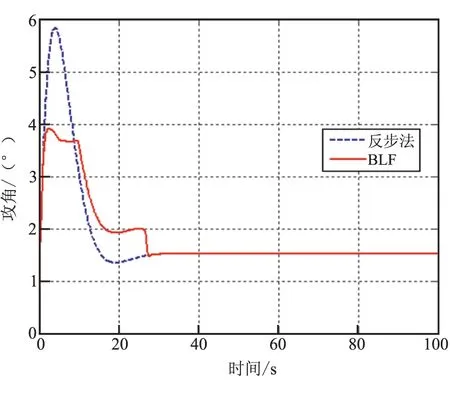
引理1:对于正数kbi,i=1,2,…,n,存在开集E={e∈Rn:|ei| (26) 其中,f:R+×N→Rn且f(t,e)为关于t的分段连续函数。在R+×N上f(t,e)关于e满足局部Lipschitz条件,关于t一直连续。假设在开集Ei:={ei∈R:|ei| (27) 式中γ1和γ2为K∞类函数。 令 如果下列不等式成立: (28) 那么ei(t)满足对任意t∈[0,∞],ei∈(-kbi,kbi)。 假设3:所给定的跟踪指令γd及γd的各阶导数有界,即存在正数A0,A1,A2,…,An,…满足: 定理:在系统的输入指令为γd且满足假设3的条件下,由式(6)~式(8)及式(23)所组成的闭环系统,若初始条件e(0)∈Ωe,e=[e1,e2,e3],Ωe={e(0)∈R3:e2(0) (1)所有的误差信号e(t)有界; (2)状态α有界,且满足 (3)闭环系统所有信号有界; (4)当t→∞时,γ→γd,即闭环系统误差跟踪信号渐进稳定。 证明: (29) 不等式(29)等价于: (30) 同理,可得误差信号e1(t)和e3(t)的上界: (31) (32) (3)由结论1可知,所有误差信号是有界的,根据假设3可知,输入指令是有界的,由误差信号e1的定义可得到状态γ是有界的。虚拟控制输入u1中,γd、γ、e1有界。所以u1有界。同理可依次推出各控制信号和各状态有界。 2.3指令滤波器 由BLF反步法倾角跟踪控制器设计的表达式可知,控制器完成闭环稳定跟踪,不仅需要被控对象的各个状态信息,而且还需要跟踪指令的各阶导数。对于三阶控制系统,控制器的输入为系统状态和跟踪指令以及指令的一阶、二阶、三阶导数。为实时计算指令的导数,在此引入三阶指令滤波器: (33a) (33b) 指令滤波器的输出作为控制系统的跟踪指令,其中输出y1为指令,y2为指令的一阶导数,y3为指令二阶导数,指令的三阶导数可表示为 a1(y1+r)+a2y2+a3y3 由式(25)可知,在BLF控制器控制下,控制系统响应中攻角的响应范围与控制器参数和输入指令的一阶导数有关。所以为了跟踪过程中实现对攻角的约束控制,还需要对控制指令的一阶导数加以限制。指令滤波器的输出y2是指令的一阶导数,所以在指令滤波器的输出y2上加入饱和限制: (34) 式中ks为待定的参数。 仿真中使用的飞行器模型是NASA公布的winged-cone,仿真中使用的气动数据是在表1的条件下计算获得,表1中同时列出飞行器参数。BLF控制器参数见表2。仿真中使用的指令滤波器为式(35)。 飞行控制任务: (1)完成对航迹倾角的无差跟踪; (2)在跟踪过程中满足飞行器攻角不超出±4°。 表1 飞行器初始条件 表2 BLF控制器参数 (35a) (35b) 根据航迹倾角跟踪时对攻角的要求|α|<4和式(32)可得 (36) 把根据表1计算而得的气动系数和表2中的控制参数代入式(36)可得 (37) 所以,把指令滤波器设y2的饱和限制参数设为ks=0.265。 下面给出飞行器跟踪不同航迹倾角指令的跟踪仿真结果。 图1和图2显示,当航迹倾角指令不断变大时,飞行器响应的攻角峰值也不断变大,且不断趋近于4°,但在BLF控制器的约束下,攻角始终小于4°。指令滤波器的输出y2的限幅是一种理想的阈值截止限制方法,这使得航迹倾角的跟踪过程中出现了不平滑的现象。 图1 航迹倾角 图2 攻角 下面用反步法航迹倾角跟踪控制系统进行仿真,并将反步法和BLF方法的仿真结果进行对比,来验证BLF控制方法的控制性能。仿真中,航迹倾角指令为5°。 图3显示2种方法都能使飞行器无稳态误差的跟踪阶跃指令,但BLF方法的瞬态响应速度不如反步法。图4显示,反步法在跟踪5°航迹倾角指令时,攻角的峰值已经超出了控对攻角的要求范围,但BLF方法中,攻角被限制在要求范围内。BLF方对航迹倾角跟踪响应中的攻角运动范围进行了限制,使得提供给飞行器的气动力的大小受到了限制,造成了BLF方法在跟踪航迹倾角时动态响应变慢。这种响应变慢并不是由于控制器造成的,而是控制要求对攻角的限制造成。图5给出了飞行器俯仰角速度响应曲线,图6是飞行器舵偏曲线,图7是控制器设计中引入的虚拟控制指令,这些曲线说明闭环系统中各个状态和控制信号都是稳定的。 图3 航迹倾角 图4 攻角 图5 俯仰角速度 (1)本文针对超燃冲压发动机作为推力装置的高超声速飞行器,使用障碍Lyapunov函数(BLF)方法,设计了一种带有攻角限制的飞行器航迹倾角跟踪控制器。该方法可有效保证高超声速飞行器在飞行控制过程中,超燃冲压发动机工作所需要的攻角约束条件。文中在给出控制方法设计的同时,对控制器稳定性给出了分析,并给出控制状态|α|的上界和控制器参数的关系。 图6 舵偏 图7 虚拟控制信号 (2)在对不同航迹倾角的跟踪响应中,BLF控制器可实现飞行器对航迹倾角的无差跟踪。对比仿真中的结果显示在响应过程中,使用传统反步法控制的飞行性的攻角超出了4°,破坏了超然冲压发动机的正常工作对攻角的要求;而BLF控制方法控制的飞行器,在跟踪过程中,攻角能按照控制要求将攻角限制在约束范围内。 [1]常军涛,于达仁,鲍文.攻角引起高超声速进气道不起动/再起动特性分析[J].航空动力学报,2008,(23)5:289-295. [2]Kogiso K,Hirate K.Reference governor for constrained systems with time-varying refereces[J].Robotics and Autonomous systems,2009,57(3):289-295. [3]Alicia Zinnecker,Andrea Serrani.Combined reference governor and anti-windup design for constrained hypersonic vehicles models[R].AIAA 2009-6283. [4]Mayne D Q,Rawlings J B,Rao C V,et al.Constrained model predictive control:Stability and optimality[J].Automatica,2000,36(6):789-814. [5]Blanchini F.Set invariance in control[J].Automatica,1999,35(11):1747-1767. [6]Dehaan D,Guay M.Extremum-seeking control of state-constrained nonlinear systems[J].Automatic,2005,41(9):1567-1575. [7]Adetola V,Guay M. Parameter convergence in adaptive extremum-seeking control[J].Automatic,2007,43(1) 105-110. [8]Ngo K B,Mahony R,Jiang Z P.Integrator backstepping using barrier functions for systems with multiple state constraints[C]//Proceedings of the 44th IEEE Conference on Decision and Control,and the European Control Conference.Seville,Spain:IEEE,2005.8306-8312. [9]Tee k P,Gea S S,Tay E H.Barrier Lyapunov functions for the control of output-constrained nolinear systems[J].Automatica,2009,45(4):915-927. [10]Ren B,Ge S S,Tee K P,et al.Adapticve neural control for output feedback nonlinear systems using a barrier Lyapunov functions[J].IEEE Transactions on Neural Networks,2010,21(9):1335-1339. [11]Tee K P,Ge S S.Control of nonlinear systems with full state constraint using a barrier Lyapunov functions[C]//Proceedings of the 48th IEEE Conference on Decision and Control.Piscataway,NJ:IEEE Press,2009:8616-8623. [12]Tee K P,Ge S S.Control of nonlinear systems with partial state constraints using a barrier Lyapunov function [J].International Journal of Control,2011,84(12):2008-2023. [13]Fiorentini L,Serrani A.Adaptive restricted trajectory tracking for a non-minimum phase hypersonic vehicle model [J].Automatica,2012,48:1248-1261. (编辑:吕耀辉) Hypersonic flight vehicle’s flight path angle tracking control with attack angle constraints WANG Yi-nan,CHEN Kang,FU Wen-xing,YAN Jie (School of Astronautics,Northwestern Polytechnical University,Xi’an710072,China) To overcome the attack angle constraints,this paper uses the barrier Lyapunov function(BLF)to study an flight path tracking control method under attack angle constraints.The hypersonic flight vehicle model was partially linearized to obtained the parameterized control model that agrees with the strict feedback form.BLF backstepping method is used to design the flight path angle tracking controller that has attack angle constraints.Stability of closed loop system was proved and the relationship between scope of attack response and controller’s parameters was established.The flight path angle tracking simulation uses the backstepping method so as to compare it with the BLF.The simulation results show that the BLF similar performances in term of steady-state error, but the BLF can restrict the attack angle within the required condition. attack constraint;flight path angle tracking;barrier Lyapunov function;backingstepping controller 2015-07-09; 2015-10-25。 国家自然科学基金青年基金(61503302)。 王易南(1969—),男,博士,研究方向为飞行器导航、制导与控制。E-mail:domo_fin@163.com V249.1 A 1006-2793(2016)01-0125-06 10.7673/j.issn.1006-2793.2016.01.023
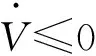
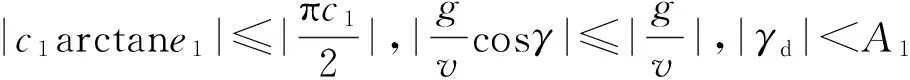
3 控制器仿真验证



4 结论