壁面障碍物对燃气弹射流场和内弹道的影响①

李仁凤，乐贵高，马大为，王　辉 ，胡晓磊

(1.南京理工大学 机械工程学院，南京　210094；2.中国航天科技集团公司七院研发中心，成都　610100)



壁面障碍物对燃气弹射流场和内弹道的影响①

李仁凤1，乐贵高1，马大为1，王辉2，胡晓磊1

(1.南京理工大学 机械工程学院，南京210094；2.中国航天科技集团公司七院研发中心，成都610100)

为了研究发射筒壁面障碍物对燃气弹射初容室内二次燃烧流场、载荷和内弹道的影响，采用k-ωSST 湍流模型和有限速率/涡耗散模型，建立考虑导弹运动的燃气弹射二次燃烧数值模型。通过与实验数据对比，验证了模型的可靠性。分析了有/无壁面障碍物和5种不同障碍物高度对燃气弹射流场、载荷和内弹道的影响。数值结果表明，无障碍物时，燃气沿着发射筒的壁面运动；有障碍物时，燃气的运动方向变为沿着燃气发生器壁面的运动，消除了燃气对发射筒以及导弹底部的2次压力峰值的冲击影响，延长了发射装置的寿命，同时延迟了导弹出筒时间，减小了出筒速度；通过对5种不同障碍物高度下弹射过程流场计算，得到300 mm障碍物高度时，导弹出筒时间较短，载荷变化平稳，且出筒速度较高。研究结果可为燃气弹射内弹道设计优化提供理论基础。

燃气弹射；二次燃烧；内弹道；壁面障碍物；动网格技术

0　引言

燃气弹射是一种利用燃烧固体火药产生的高压气体作为导弹运动动力源的弹射系统，具有反应快、装置简便、出筒速度高以及易满足内弹道要求等优点，广泛用于国内外武器弹射装置中。燃气弹射属于冷发射技术，为了防止高温燃气对导弹底部和发射装置产生热烧蚀，目前大多采用填充有低温推进剂的燃气发生器作为动力源将导弹弹射出发射筒，减小高温燃气带来的热烧蚀。适用于水下发射、陆地机动发射车发射以及地下井发射等[1-3]。

针对燃气弹射的研究，国内外主要采用理论分析与实验研究的方法。袁曾凤[4]、芮守祯[5]等主要建立了弹射内弹道模型，分析了弹射内弹道曲线变化规律。由于经典内弹道理论只能获得内弹道曲线，无法得知弹射过程中流场的具体分布形态，在此基础上，谭大成[6]针对二维低压室弹射内弹道数值模型进行了研究，对单组分低压室内气体流动规律进行了分析。随着低温推进剂的采用，燃气发生器喷出的燃气并不只是单一的组分，经常含有大量未燃烧完全的气体，它们与初容室中的空气混合会发生二次燃烧现象[7-8]，造成初容室内载荷增加，影响弹射导弹的内弹道参数。因此，胡晓磊等[9]建立了燃气弹射二次燃烧数值模型，对比分析了有无二次燃烧对内弹道特性的影响。

对于低温推进剂燃气弹射装置，发射筒的结构形式对燃气运动过程影响较大。通过改变发射筒结构，可改变燃气发生器喷出的燃气与初容室中空气的接触过程，从而影响二次燃烧反应的形态，控制弹射载荷以及内弹道的变化规律，因此有必要对低温推进剂发射筒结构进行优化设计。本文以燃气弹射装置为物理模型，采用有限速率/涡耗散模型建立包含导弹运动的弹射装置二次燃烧模型，并研究了壁面障碍物对燃气弹射流场、内弹道和载荷特性的影响规律，为弹射动力装置结构优化和内弹道设计提供理论基础。

1　物理模型和计算方法

1.1基本假设与控制方程

基本假设：

(1)燃气为理想气体，服从理想气体状态方程；

(2)忽略辐射以及重力的影响；

(3)假设N2为不可燃气体；

(4)忽略燃气中固体颗粒的影响。

针对燃气弹射装置轴对称结构特点，采用有限速率涡耗散反应模型，建立二维轴对称多组分Navier-Stokes控制方程，湍流模型采用SSTk-ω模型。

(1)

其中

1.2湍流模型

针对燃气弹射过程的流场研究，主要采用SSTk-ω模型，可很好预测壁面束缚流动和自由剪切流动。SSTk-ω模型是在标准k-ω模型基础上加以改进得到的，在湍流粘度的求解中，考虑了湍流剪应力的传播，具有较高的精度及可信度[10-11]。

1.3有限速率/涡耗散模型

低温燃气射流中，包含大量未完全燃烧的燃气组分。因此，针对燃气弹射流场模型，需要考虑二次燃烧的作用。二次燃烧过程采用有限速率/涡耗散模型，忽略湍流脉动对化学反应过程的影响，反应速率根据下面的Arrhenius[12]公式确定。

(2)

(3)

(4)

式中YR为反应物质量分数；YP为燃烧产物质量分数；A为常数，A=4.0；B为常数，B=0.5。

由于该燃气弹射采用低温推进剂，目前低温推进剂二次燃烧机理尚处于研究阶段，文中气相组分燃烧模型采用文献[13]中比较符合低温推进剂的CO/H2简化燃烧模型：

2CO+O2→2CO2+Q1(Q1=565.95kJ/mol)

2H2+O2→2H2O+Q2(Q2=563.64kJ/mol)

1.4网格模型和边界条件

燃气弹射系统由燃气发生器、导流锥、发射筒、底座及尾罩组成，如图1所示。其中，取发射筒壁面上点A为实验和仿真研究的观测点。其工作原理是燃气发生器中的低温推进剂燃烧产生的高压燃气经过喷管进入初容室，与初容室中的空气混合与燃烧，推动导弹向上运动。

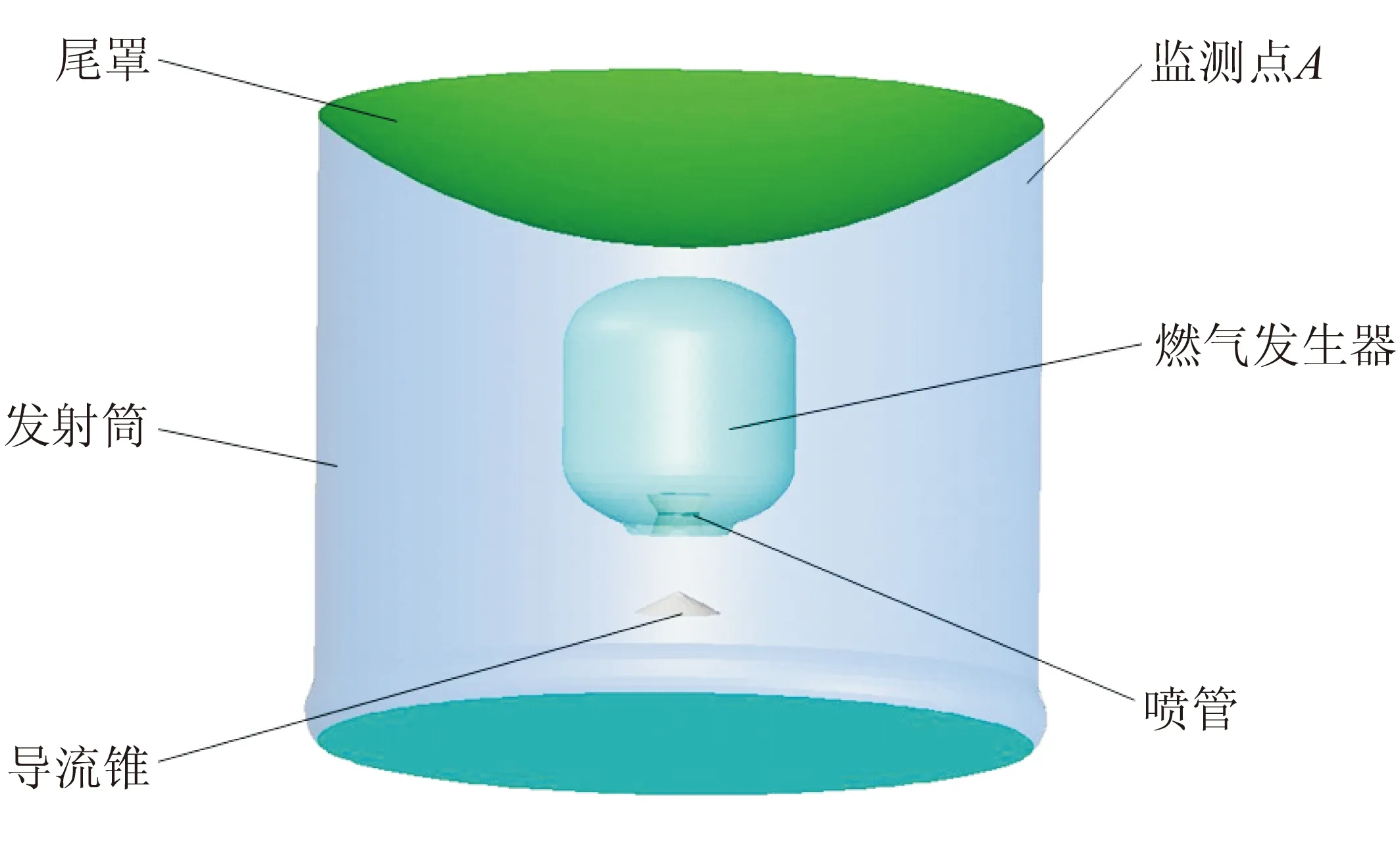
图1　燃气弹射装置结构示意图

燃气弹射二次燃烧数值计算网格模型如图2所示，采用结构网格，在喷管及壁面处进行网格加密。喷管入口采用压力入口，其总压随时间变化规律见图3。

图2　网格模型

图3　喷管入口压力曲线

燃气发生器壁面和喷管壁面均采用绝热壁面边界条件，发射筒壁面采用对流换热壁面。使用CEA软件，对推进剂燃烧产物进行热力学计算，得到喷管入口各气体组分的质量分数图4。初容室内初始压力为标准大气压101 325 Pa，温度为288.15 K，N2的质量分数为0.77，O2的质量分数为0.23。

导弹尾罩在燃气推力的作用下向上运动，弹射过程中导弹在轴线方向上受到燃气推力、重力和摩擦力的共同作用，根据牛顿第二定律，编写udf得到导弹在不同时刻向上的运动速度以及位移。同时，运用域动分层动网格技术，实现尾罩下方网格的更新[14]。

图4　喷管入口燃气组分质量分数

2　数值方法验证

为了验证数值方法的准确性，采用文中建立的数值方法，对燃气弹射流场进行计算，得到A点压力与温度计算值与实验值对比曲线(无量纲)，如图5所示。其中，p0为参考压力，取值1 MPa；t0为燃烧室燃烧完全所用时间，取值为1.1 s。

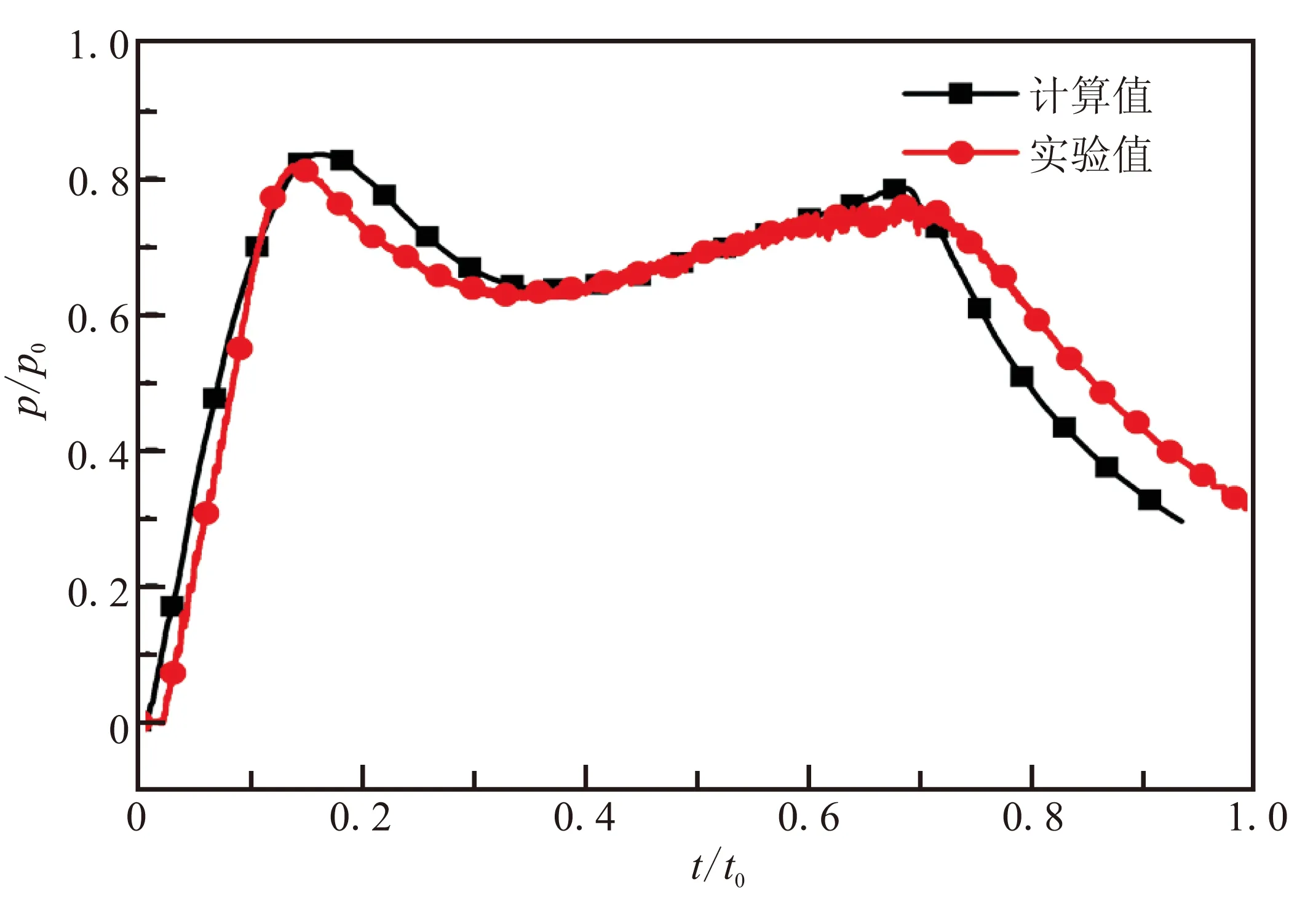
(a)压力曲线

(b)温度曲线

从图5中可看出，压力与温度的计算值与实验值的结果吻合较好。计算中，成功捕捉到了燃气弹射实验过程中存在的2个压力峰值。计算得到的第一个压力峰值为0.85p0，实验值为0.83p0；计算获得的第二个压力峰值为0.8p0，实验值为0.78p0。数值结果与计算结果在压力峰值上最大误差为2.6%。这表明建立的数值模型及采用的数值方法具有较高的精度，可用于分析壁面障碍物对弹射流场和弹道的影响。

3　计算结果与分析

3.1有无壁面障碍物弹射流场分析

图6(a)、(b)分别为0.1t0时刻有无壁面障碍物燃气弹射流线对比图和流场温度云图，每幅图的左半部分为含有壁面障碍物条件，右半部分为无障碍物条件。从不同时刻流线图可观察到，当发射筒壁面没有壁面障碍物时，以右半区为例，燃气射流在导流锥的分流作用下，一部分燃气绕到导流锥下方的低压区域，形成一个顺时针方向漩涡结构；另一部分燃气沿着发射筒壁面进入初容室，形成另一个较大的逆时针漩涡，这个漩涡的存在，使得初容室中的燃气与空气混合更加充分，加快了二次燃烧的过程。当含有壁面障碍物时，以左半区为例，经过导流锥整流后的燃气遇到底座时，发生分流，部分燃气流向轴线方向，并在导流锥和底座之间形成逆时针漩涡；另一部分沿着底座和发射筒壁面向上流动，当遇到底部障碍物，燃气流动方向发生转折，向燃气发生器壁面扩散。受燃气发生器壁面影响，燃气流发生反射，向尾罩方向流动。当燃气流遇到尾罩时，又一次发生分流，部分燃气流向轴向方向，在燃气发生器和尾罩之间区域形成逆时针漩涡，在受到上端障碍物的阻碍后，绕过障碍物向下运动，仅有一小部分燃气进入障碍物之间的区域，与氧气发生燃烧。

(a)流线图　　　　　　　　　(b)温度云图

从温度云图可见，不含有壁面障碍物时，初容室中的高温区域主要发生在发射筒壁面边界层及导流锥下方；当含有壁面障碍物时，高温区域主要发生在燃气发生器与障碍物之间的区域，发射筒附近温度相对较低。

图7(a)、(b)分别为0.1t0时刻和0.2t0时刻有无壁面障碍物燃气弹射压力云图。对比这2个时刻的压力云图可看到，含有壁面障碍物的发射筒中的压力比不含有障碍物的压力低，且发射筒中的压力分布较均匀。图8(a)、(b)分别为有无壁面障碍物弹射过程中，监测点A的压力与温度随时间变化曲线图。

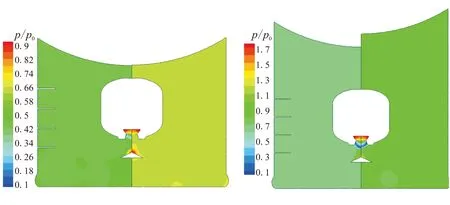
(a)0.1t0　　　　　　　　　　　(b)0.2t0

(a)压力曲线

(b)温度曲线

从图8(a)可知，无障碍物时，A点的压力曲线明显存在2个较大的压力峰值，而有障碍物时，压力曲线的变化相对平缓，消除了2个压力峰值对发射筒的冲击影响。无障碍物时，压力在0.153t0时刻达到压力峰值0.85p0；有障碍物时，压力在0.284t0时刻达到最大值0.704p0，相比无障碍物时，压力峰值到达的时间延迟了0.131t0，压力峰值减小了0.146p0。从图8(b)可看到，无障碍物条件下，A点的温度明显高于有障碍物条件下的温度。这是由于障碍物的增加，减弱了二次燃烧的进行。由于二次燃烧的作用，监测点A的最高温度均大于入口的初始温度0.4T0。其中，T0为温度参考值。

图9为0.1t0时刻燃气弹射燃烧组分H2、H2O、CO和CO2的质量分数分布云图。由不同组分质量分数云图可见，当无障碍物的影响时，CO与H2质量分数在导流锥下方以及发射筒壁面附近，相比喷管入口组分质量分数减小，而H2O和CO2在该区域质量分数比入口大，说明在该区域中，H2、CO与O2反应分别生成H2O与CO2，二次燃烧主要发生在该区域中；当含有壁面障碍物时，CO与H2的质量分数在导流锥下方以及燃气发生器壁面附近减小，而H2O与CO2在该区域质量分数较大，说明二次燃烧主要发生在发射筒底部与燃气发生器周围。由于二次燃烧主要作用位置的不同，从而导致了图8(b)温度云图所示的变化规律。

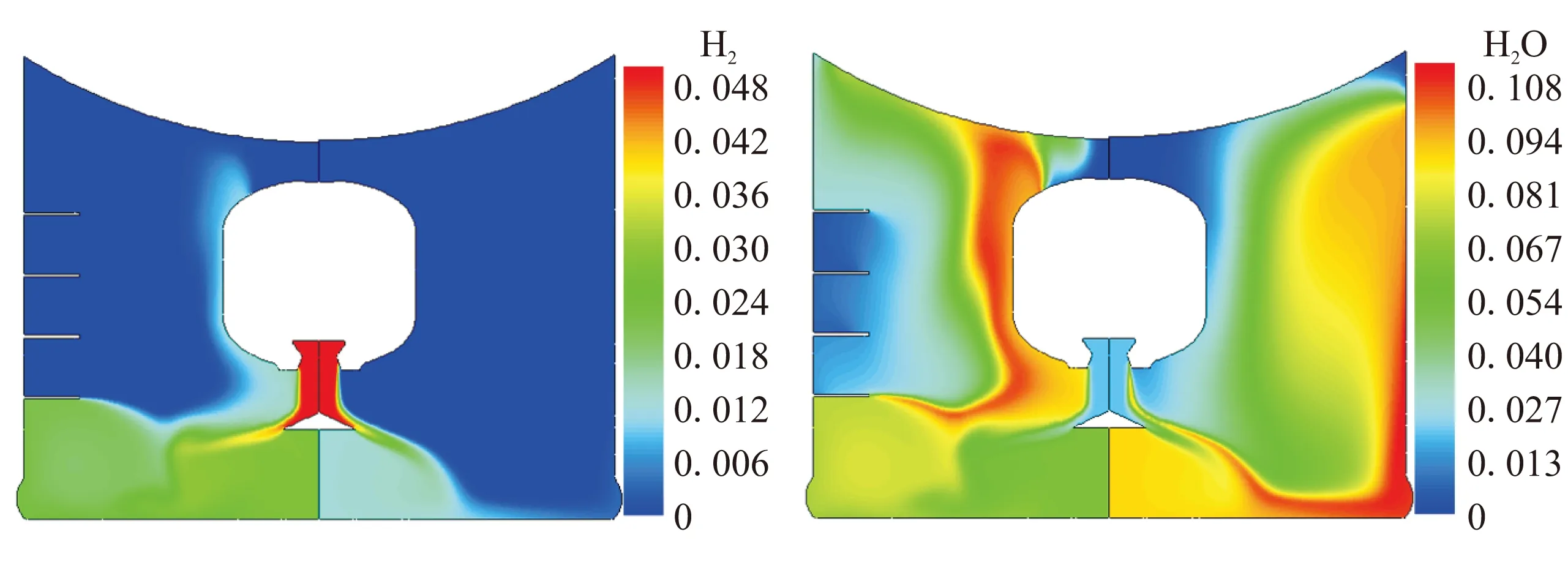
(a)H2　　　　　　　　　　(b)H2O

(c)CO　　　　　　　　　　(d)CO2

图10为弹射装置内的O2质量分数随时间变化曲线。从O2质量分数随时间变化曲线图可看到，氧气消耗速率在无障碍物条件下比有障碍物条件下快。无障碍物时，弹射装置中的O2完全消耗所用的时间为0.24t0，而有障碍物时氧气完全消耗的时间为0.48t0，因此，进一步说明了障碍物的添加，有效减缓了燃烧的进行。

图10　弹射装置O2质量分数随时间变化曲线

3.2有无壁面障碍物弹射内弹道特性分析

图11为有无壁面障碍物燃气弹射内弹道变化曲线图，导弹发射筒长为0.885l0。其中，l0为位移参考值；v0为速度参考值；a0为加速度参考值。计算在导弹出发射筒时结束。图11(a)为导弹的加速度变化曲线，该曲线的变化规律与监测点A压力的变化规律相近，说明尾罩受到的载荷与监测点A的载荷变化相近。因此，在无障碍物时，燃气对尾罩与外筒会产生两次较大的冲击，而有障碍物时，压力载荷的变化较平缓，从而加速度变化也较平稳。图11(b)为导弹的速度变化曲线，从曲线图中可看出，在同一时刻，导弹在无障碍物条件下比有障碍物时的运动速度快。无障碍物时，导弹出筒速度为0.91v0，出筒时间为0.86t0；无障碍物时，导弹出筒速度为0.85v0，出筒时间为0.92t0，相比无障碍物时，出筒时间延迟了7%，出筒速度减小了6.6%。图11(c)为导弹位移变化曲线，在同一时刻，导弹在无障碍物时的位移比有障碍物时大。因此，无障碍物时，导弹提前出筒。由此可见，障碍物的添加，消除了燃气对发射筒以及导弹的载荷2次冲击影响，延长了发射装置的寿命，同时也延迟了导弹出筒时间，减小了导弹的出筒速度。

3.3不同障碍物高度弹射载荷与内弹道特性分析

为了分析障碍物高度对燃气弹射载荷及内弹道特性的影响，分别选取150、200、250、300、350 mm这5种不同障碍物高度弹射装置进行数值分析。图12为5种不同障碍物高度下监测点A的压力变化曲线。从压力曲线图可看出，当障碍物高度由150 mm增加到300 mm时，压力曲线的峰值逐渐减小，压力峰值的变化逐渐趋于平缓；当障碍物高度增加为350 mm时，初容室内观测点压力曲线偏离理想压力曲线，且仍存在载荷变化的不平稳。

(a)加速度

(b)速度

(c)位移

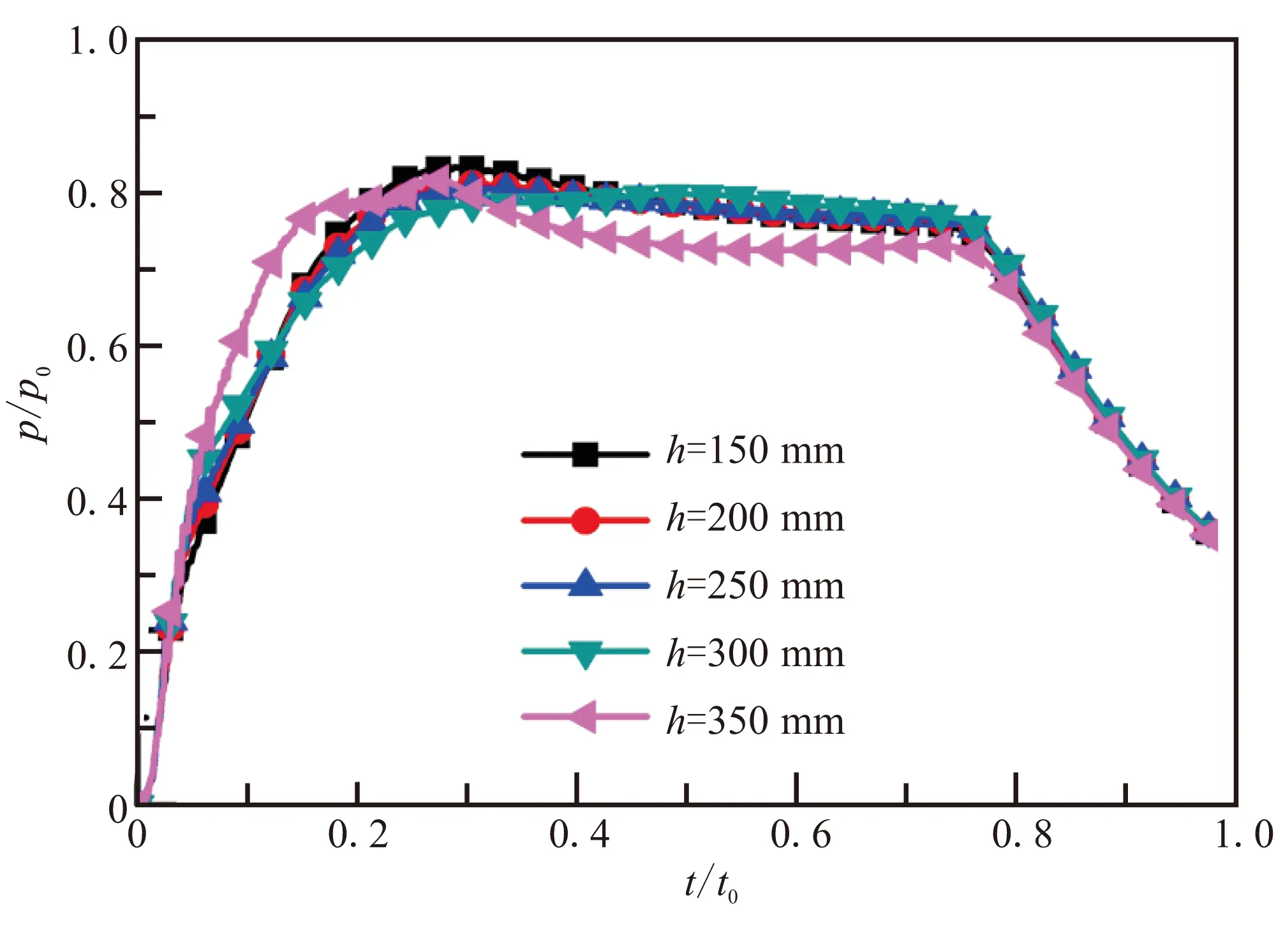
图12　不同障碍物高度监测点A压力曲线

图13为5种不同障碍物高度下弹射装置中O2质量分数随时间变化曲线，由图13可见，当障碍物高度处于150～300 mm之间时，O2质量分数下降速率相近，没有太大变化，当高度增加为350 mm时，O2质量分数下降速率增加，二次燃烧速率加快，从而导致了压力曲线图中峰值相对升高。

图14为5种不同障碍物高度下燃气弹射载荷与内弹道变化曲线。

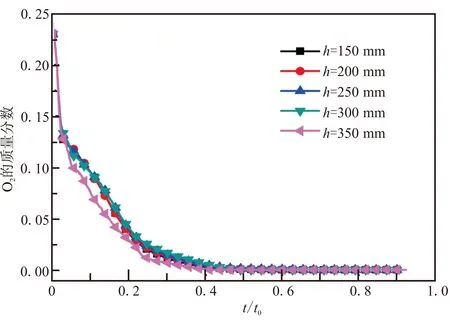
图13　5种不同高度下O2质量分数曲线

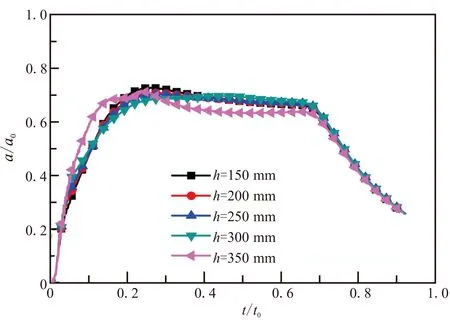
(a)加速度曲线

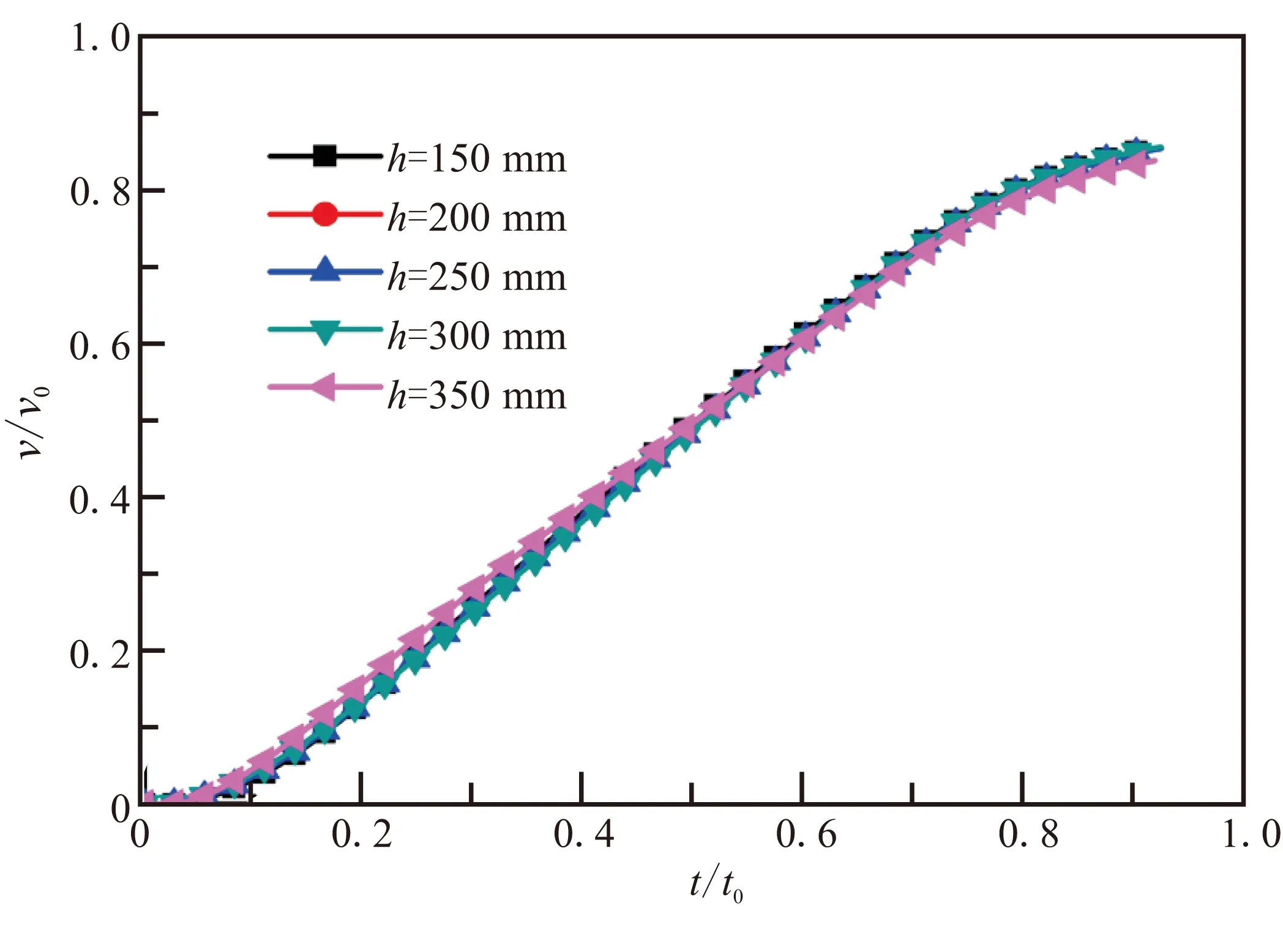
(b)速度曲线

图14(a)为导弹加速度变化曲线，与监测点A压力变化曲线保持一致，无障碍物时，加速度会有两次较大的冲击影响，有障碍物时，加速度最大值变化较平稳。图14(b)为导弹运动速度变化曲线，可看到在不同障碍物高度下，速度变化曲线相近，导弹出筒时间与出筒速度相对变化较小。

表1给出了5种不同障碍物高度下所对应的导弹的最大加速度、出筒速度和出筒时间，根据给定的该型号导弹内弹道要求，出筒速度应在0.8v0～0.95v0范围内，加速度峰值不大于0.98a0。由表1可见，5种工况均满足内弹道要求，但综合考虑载荷变化的影响，可见障碍物高度为300 mm时，出筒速度较高，出筒时间较短以及载荷变化平稳，为最优结构方案。

表1　5种不同高度下内弹道数据对比

4　结论

(1)建立了考虑导弹运动的二次燃烧燃气弹射内弹道数值模型，采用SSTk-ω湍流模型、有限速率/涡耗散模型以及动网格技术对燃气弹射初容室内二次燃烧过程进行了数值分析，通过与实验数据对比，验证了数值方法的可靠性。

(2)分析了发射筒有/无障碍物模型下初容室内流场和内弹道变化规律。结果表明，添加障碍物使得弹射装置中燃气沿着燃气发生器壁面运动，减缓了燃烧的进行，消除了对发射筒及导弹的2次压力峰值冲击影响，延长了发射装置的寿命，但导弹出筒时间相比无障碍物时延迟了7%，导弹出筒速度减小了6.6%。

(3)分别对5种不同障碍物高度下的燃气弹射过程进行了数值研究。随着障碍物高度的增加，压力变化逐渐平稳，但增加到超过350 mm，会出现较大的峰值。计算得到了5种障碍物高度下导弹的出筒数据，根据给定内弹道要求，结合载荷变化规律，得到300 mm障碍物高度时，出筒时间较短，载荷变化平稳及出筒速度较高，为最优结构。

[1]李广裕.战略导弹弹射技术的发展[J].国外导弹与航天运载器,1990(7):38-49.

[2]蒋瑞岗.导弹的弹射与燃气发生器设计[J].现代防御技术,1998(5):9-16.

[3]McKinnis J A,O’Connell A R,Martin Marietta.MX launcher gas generator concepts[R].AIAA 81-8157.

[4]袁曾凤.弹射内弹道中的相似方法研究[J].兵工学报,1987,8(2):8-18.

[5]芮守祯,邢玉明.几种导弹弹射动力系统内弹道性能比较[J].北京航空航天大学学报,2009,35(6):766-770.

[6]李峥,向红军,张小英.复合推进剂固体火箭发动机喷流流场数值模拟[J].固体火箭技术,2014,37(1):37-42.

[7]高凯,周成康,邓科,等.同心筒内二次燃烧对导弹运动的影响分析.导弹与航天运载技术,2014(2):23-26.

[8]谭大成,苗佩云.弹射器低压室二维内弹道模型及数值研究[J].弹箭与制导学报,2006,26(4):224-226.

[9]胡晓磊,乐贵高,马大为,朱忠领.同心筒发射燃气射流二次燃烧数值研究及导流板改进[J].兵工学报,2014,35(1):62-69.

[10]Menter F R,Kuntz M,Langtry R.Ten years of experience with the SST turbulence model[J].Heat and Mass Transfer,2003(4):625-632.

[11]Samy M El-Behery,Mofreh H Hamed.A comparative study of turbulence models performance for separating flow in a planar asymmetric diffuser[J].Computers and Fluids,2011,44:248-257.

[12]苗瑞生.发射气体动力学[M].北京：国防工业出版社,2006.

[13]冯喜平,李海波,唐金兰,等.采用不同气相燃烧模型模拟含硼燃气扩散燃烧过程[J].固体火箭技术,2013,36(4): 474-480.

[14]姜毅,郝继光,傅德彬.导弹发射过程三维非定常数值模拟[J].兵工学报,2008,29(8):911-915.

(编辑：薛永利)

Influence of tube-wall obstacles on flow field of gas-ejection and internal trajectory

LI Ren-feng1，LE Gui-gao1，MA Da-wei1，WANG Hui2，HU Xiao-lei1

(1.School of Mechanical Engineering，NUST，Nanjing 210094，China；2.Aerospace Science and Technology Corporation，the Seventh Research Institute and Development Center，Chengdu610100，China)

To study the influence of tube-wall obstacles on secondary combustion of gas-ejection,load and internal trajectory characteristics,SSTk-ωturbulence model and the finite-rate/dissipation model were adopted to build the secondary combustion model with missile moving. Compared with experimental data, it shows that the model is reliable. The influence of tube-wall obstacles and the height of obstacles on flow-field,load and internal trajectory were analyzed.Results show that when ejection launcher has no obstacles,gas moves along the tube wall;when ejection launcher has obstacles,gas moves along the gas generator wall,influence of gas on two pressure peaks in the launching tube and in the missile bottom are eliminated and the life of launcher is extended. However,the time out of tube delays and the velocity out of tube decreases.Moreover,through the analysis of five different height conditions of obstacle,when the height of obstacle is 300 mm,the time out of tube is the shortest,load is steady and the velocity out of tube is the largest.The results provide theoretical basis for interior ballistic optimal design of gas-ejection.

gas-ejection；secondary combustion；internal trajectory；wall obstacles；dynamic mesh technology

2015-04-29；

2015-06-07。

国防基础科研项目。

李仁凤(1989—)，女，博士，研究方向为兵器发射理论与技术。E-mail：lirenfeng443@163.com

V553

A

1006-2793(2016)03-0444-07

10.7673/j.issn.1006-2793.2016.03.028