基于代理模型的固体火箭发动机装药设计①

武泽平，王东辉，胡　凡，张为华

(国防科技大学 航天科学与工程学院，长沙　410073)



基于代理模型的固体火箭发动机装药设计①

武泽平，王东辉，胡凡，张为华

(国防科技大学 航天科学与工程学院，长沙410073)

提出一种基于代理模型的固体火箭发动机装药优化设计方法。将代理模型技术用于基于Level Set的固体火箭发动机装药设计，并提出了基于Pareto前沿采样的并行加点准则，进一步提升算法性能。以后翼柱型装药为例，以推力平稳为设计目标，得到了优良的推力性能，验证了方法的有效性。

固体火箭发动机；代理模型；并行加点准则；优化设计方法；LevelSet；装药设计

0　引言

固体火箭发动机设计是火箭/导弹设计的重要内容，发动机设计质量好坏直接影响火箭/导弹性能。装药设计是固体火箭发动机设计的重要组成部分，对固体火箭发动机性能的优劣起着决定性作用[1]。装药设计与发动机总体设计联系密切，往往在发动机总体方案论证时，就已确定了推进剂的配方，甚至选定了药型。在通常情况下，装药设计最主要的任务是确定药型尺寸，使其满足一定的内弹道性能。在过去的几十年里，形成了一系列的装药设计方法[2-4]，此类方法通常采用智能优化方法驱动计算量较小的低精度燃面退移仿真方法进行装药设计，需要大量的迭代计算，且计算精度难以保证。

随着高性能计算技术不断发展和广泛应用，发动机仿真计算精度明显提高，利用计算机技术进行发动机优化设计，以寻求性能优良、结构可靠的发动机设计方案。然而，精确仿真模型往往具有计算复杂度高、计算耗时长的特点。此时，智能优化方法的大量迭代计算通常难以接受[5]。代理模型技术可通过设计空间少量样本点，对全空间输出进行预测，在优化过程中，能大量降低模型仿真次数，对基于大计算量高精度模型的优化设计，能显著提高优化设计的效率。

本文将基于代理模型的高效优化方法引入固体火箭发动机装药设计过程中，为进一步提升优化性能，提出并行加点准则。最后，以后翼柱型装药为例，验证本文方法的有效性。

1　优化计算模型

1.1基于LevelSet的燃面计算方法

燃面计算是固体火箭发动机设计的重要环节，其方法优劣直接影响发动机内弹道性能的预估及发动机装药设计品质。燃面推移是一个复杂的过程，推移过程中伴有燃面的消失和新燃面的生成，导致燃面结构剧烈变化[6]。

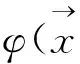
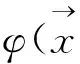
代理模型技术通过少量样本点的输入输出特性，对整个设计空间响应进行预测，将其引入优化设计过程，可有效减少模型调用次数。对基于复杂耗时模型的优化设计，可显著提高设计效率。本文将代理模型技术引入基于LevelSet燃面计算的固体火箭发动机装药优化设计，并提出高效的并行加点准则，进一步提高优化设计效率。

1.2弹道计算方法

零维内弹道计算的基本微分方程组如下：

(1)

(2)

(4)

1.3优化目标与约束

以往的装药设计目标通常是发动机性能最优，而不关心推力随时间的变化规律。因此，在装药燃烧过程中，往往会出现由于燃面的消失和新燃面的生成导致推力发生震荡的现象，而这往往是弹/箭总体设计中应尽量避免的。因此，本文将发动机工作过程中的推力平稳性作为优化目标，同时将发动机的性能作为约束进行优化设计，以期满足弹/箭总体设计需求。具体实施过程中，本文将设计发动机推力与总体要求平均推力之间的偏差最小化作为优化目标，其数学表达式如式(5)所示。其中，T为发动机工作时间，考虑到发动机点火和耗尽时不可避免会出现推力迅速变化的情况，本文略去开始工作后5%和工作结束前10%的推力变化影响。

(5)

其中，x为设计变量，即装药的几何构型参数。设计约束为装药性能参数，包括马赫数M、装填系数J、喉通比η以及装药质量mp。

上述参数均为装药几何构型参数的函数。因此，本文构建的优化模型如式(6)所示。其中，M0、J0、η0和mp0为总体设计给出的各参数临界值。

min:f(x)

J(x)>J0

(6)

2　基于代理模型的优化设计方法

LevelSet对复杂三维药型燃面计算有较高精度。然而，由于计算相对较为耗时，目前对基于该方法的装药设计方法仅有少量研究。本文将代理模型技术引入装药设计过程中，可有效减少LevelSet燃面计算模型调用次数，实现基于LevelSet的固体发动机装药优化设计。基于代理模型的优化设计方法主要由数据与处理、近似建模和序列加点3部分构成，算法流程如图1所示。

数据预处理阶段进行采样点的选择，不同设计变量尺度的统一，以及在采样点运行模型得到模型输出，为近似建模提供训练样本。

近似建模阶段分为近似模型的构造和验证。首先，通过插值或拟合技术，根据训练样本对设计空间的输出进行预测；其次，最小化验证样本点预测误差进行参数选优与模型验证。

采样点更新阶段的核心是构造用于加密采样点的优化问题，即加点准则。当加点准则确定后，采用一种高效的内优化算法(通常为全局优化能力较强的智能优化算法)，根据加密准则，选择下一采样点。

收敛准则用来终止算法迭代，高效的收敛准则可大量减少不必要的计算消耗。本文采用二步收敛判定方法[16]：新点的加入对代理模型是否起到更新作用；新点的加入能否够提高最优点处代理模型近似性能。

该收敛判定准则能有效减少复杂模型调用次数，提高优化设计效率。

图1　基于代理模型的优化设计流程

2.1最优拉丁超立方实验设计

基于代理模型的优化方法中，实验设计是其前处理步骤，合理的实验设计手段可有效选择初始采样点，提高近似模型对样本点信息的利用效率[7]。由于拉丁超立方设计(Latin Hypercube Sampling, LHS)任意设计变量个数均能自由设计采样点个数,因此在安排计算机仿真实验中应用最广。

LHS在采样空间中，将每一个设计变量等分成个间隔(水平)。首先，在每个变量的N个等间隔中，随机选取一个不重复的间隔，按均匀分布随机产生一个样本点，循环N次，即可得到N个样本点。为了保证采样点的空间均匀分布特性，需要对拉丁超立方进行合理设计，即优化拉丁超立方设计。近年来，有大量学者对此进行了研究[8-14]，本文不再赘述，仅将其成果用于构造优化拉丁超立方设计。

为了避免不同变量之间数量级差异对近似模型精度的影响，在实验设计之前，对所有变量进行归一化处理；之后，所有过程均在归一化后的N维单位超立方中进行。

2.2代理模型构造方法

代理模型的本质是多变量函数逼近，径向基函数插值方法本质上采用一元函数来对多元函数进行描述[15]，在多变量函数逼近中发挥着重要作用。径向基插值可表示为

(7)

其中，N为采样点个数；wk为每个样本点的权系数；φk(rk)为基函数。其中，rk表示点x距中心点xk的欧氏距离。将所有采样点xk的响应值yk代入式(7)，得方程组

(8)

其中，φk(rik)为基函数，本文采用式(9)所示的高斯函数。

(9)

c为基函数的形状参数，本文采用Wang等[16]提出的方法进行确定。为了增加径向基函数插值对带随机误差数据点的逼近能力，在求解方程组(8)时，引入正则化项，即在系数矩阵加上充分小的对角阵Λ(通常取0.001I)，使其能够处理带有随机误差的数据，其物理意义为在考虑模型对样本点的逼近程度的同时，增加模型的光滑性。此时，径向基插值的模型为

(10)

通过求解方程组(10)，可得系数w，将其代入式(7)，可得输出的代理模型。

2.3并行加点准则

加点准则的构造是基于代理模型优化设计中的关键技术，合理的加点准则不仅能有效提高代理模型的全局精度，而且能对最优解做出快速预测，已有的加点准则多为单点加点准则[17-19]，效率低下。本文针对此问题，提出一种基于Pareto前沿采样的并行加点准则。

目前，单点加点准则主要有探索准则、开发准则和平衡准则，探索准则侧重在采样点稀疏区域进行加点，开发准则侧重在代理模型的最优解处加点，平衡准则是对二者的折中。本文提出的并行加点准则使加点过程同时具备探索和开发能力，具体实施如下。

构造多目标优化问题(11)，其解为图2所示的Pareto前沿。

(11)

其中，s(x)为代理模型输出，最大化s(x)导致采样点向代理模型预测的最优区域聚集，使该准则具备开发能力，d(x)为下一采样点与历史采样点之间的最小距离，最大化d(x)导致采样点向未采样区域探索，使该准则具备探索能力。因此，通过求解问题(11)得到的最优解(即图2中Pareto前沿上的点)，同时具备探索和开发能力；之后，在Pareto最优解中，选取n个点进行下一轮迭代计算，n为并行计算节点个数。

图2　基于Pareto前沿加点示意图

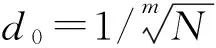
3　测试算例分析

3.1药柱参数化建模方法

后翼柱型装药构型如图3所示。在不考虑加工过程中倒圆倒角的情况下，图3中尺寸、前后封头椭球比以及后翼个数与翼宽，可唯一确定装药的几何构型。

图3　后翼柱型装药几何构型

由于实际应用中，上述参数彼此不能独立变化。因此，优化过程中，独立参数选择L1、L13、L12、D1、R6、翼宽Bw，其余参数固定不变。

给定装药配方后，装药密度已知，L1、D1的范围根据装药体积Vp、马赫数M及装填系数J等性能指标确定，如式(12)所示。为防止尺寸欠约束导致建模干涉，本算例不以实际尺寸为设计变量，采用比例映射方式处理其余各尺寸参数，优化过程中，除L1、D1外，各设计变量如(13)所示。

(12)

(13)

经过式(13)处理后的各设计变量范围均可在0～1之间变化，且有效避免了建模干涉问题，是对此类构型进行参数化的有效方法。

根据本文提出的方法，装药优化设计计算步骤如下：

(1)采用优化拉丁超立方实验设计选取采样点，在样本点出计算目标函数和所有约束值；

(2)通过样本点的输出值，根据2.2节的方法构造目标函数和约束的代理模型；

(3)采用NSGA-II算法，运行2.3节的并行加点，采样点个数选择为6；

(4)计算终止判定，是，停止计算，输出最优解；否，返回(2)，重新构造代理模型。

3.2优化设计与分析

本算例采用8片翼的后翼柱装药构型，设计输入指标如表1所示。其中，推力、总冲、工作时间为设计指标，装药相关参数由装药配方给出，喉径和膨胀比为总体优化设计给出的最优结果。

优化设计初始采样点个数为48，并行计算节点数为6，最大模型仿真次数设置为300，目标函数迭代曲线如图4所示，当模型调用次数为198次时，算法收敛。最优解如表2所示。

图4　优化目标迭代曲线

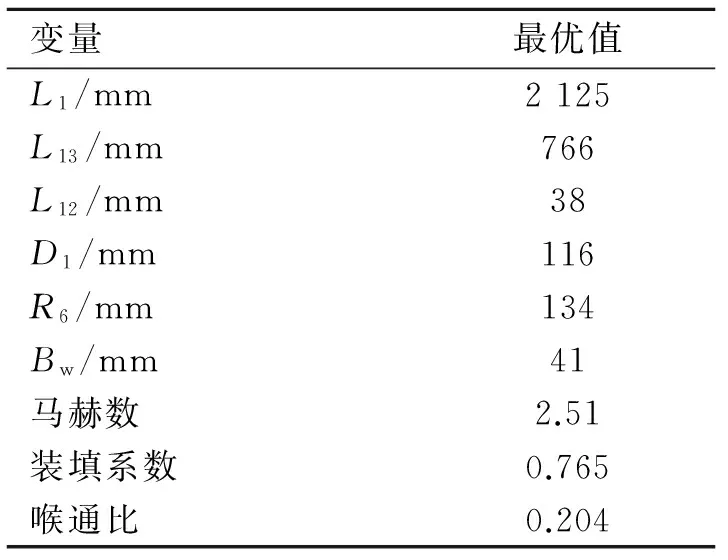
表2　优化设计结果

最优装药构型对应的内弹道曲线和燃面-时间曲线如图5和图6所示。

图5　最优推力曲线

图6　最优燃面曲线

由图5和图6可得，推力和燃面曲线较平稳，无明显波动，表明优化算法性能良好。

根据最终得到的推力曲线，与设计输入的总体指标进行对比，结果如表3所示。由表3可得，各相对误差均在1%以内，二者吻合较好。表明该方法是对固体火箭发动机装药设计的有效方法。

表3　计算性能结果对比

4　结论

(1)将代理模型引入固体火箭发动机装药设计，使基于LevelSet高精度燃面计算的应用成为现实，提高了固体火箭发动机装药设计精度。

(2)提出了基于Pareto前沿并行加点的序列加点准则，将其用于基于代理模型的装药设计，仅一百多次高精度仿真，即可找到最优解。相比常规智能算法，大大减少了迭代次数。

(3)基于推力匹配的思想，对后翼柱装药进行优化，完成固体火箭发动机装药设计，设计推力与推力需求能很好地匹配，且总体指标也能很好的吻合，验证了算法的有效性，丰富了固体火箭发动机装药设计方法。

[1]王有元. 固体火箭发动机设计[M]. 北京: 国防工业出版社, 1984.

[2]王鹏，李旭昌，徐颖军. 固体火箭发动机总体优化设计[J]. 火箭推进, 2007, 33(4): 16-19.

[3]高波，叶定友，侯晓，等. 固体火箭发动机三维药柱燃面自动化设计方法研究[J]. 推进技术, 1998, 19(6): 24-26.

[4]杨涓，戎海武，朱燕堂，等. 固体发动机药柱优化设计[J]. 推进技术, 1997, 18(2): 98-102.

[5]Alexander I J, Forrester, Keane A J. Recent advances in surrogate-based optimization[J]. Progress in Aerospace Sciences, 2009, 45(1-3): 50-79.

[6]费阳. 含裂纹固体火箭发动机性能分析[D]. 长沙: 国防科技大学, 2010.

[7]武泽平. 序列近似方法及其应用研究[D]. 长沙: 国防科技大学, 2013.

[8]刘晓路，陈英武，荆显荣，等. 优化拉丁方试验设计方法及其应用[J]. 国防科技大学学报, 2011, 33(5): 73-77.

[9]孙法省. 模型未知下试验设计的构造[D]. 南开大学, 2010.

[10]刘新亮，郭波. 基于改进ESE算法的多目标优化试验设计方法[J]. 系统工程与电子技术, 2010, 32(2): 410-414.

[11]刘新亮，郭波. 适用于复杂系统仿真试验的试验设计方法[J]. 国防科技大学学报, 2009, 31(6): 95-99.

[12]Sun F, Liu M, Lin D K J. Construction of orthogonal Latin hypercube designs[M]. Biometrika, 2009.

[13]Grosso A, Jamali A, Locatelli M. Finding maximin Latin hypercube designs by Iterated Local Search heuristics[J]. European Journal of Operational Research, 2009, 197(2): 541-547.

[14]Cioppa T M, Lucas T W. Efficient nearly orthogonal and space-filling latin hypercubes[J]. Technometrics, 2007, 49(1): 45-55.

[15] 穆雪峰. 多学科设计优化代理模型技术的研究和应用[D]. 南京航空航天大学, 2004.

[16]Wang D, Hu F, Ma Z, et al. A CAD/CAE integrated framework for structural design optimization using sequential approximation optimization[J]. Advances in Engineering Software, 2014, 76: 56-68.

[17]Jones D R. A taxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization, 2001, 23: 345-383.

[18] 武泽平，王东辉，杨希祥，等. 应用径向基代理模型实现序列自适应在采样优化策略[J]. 国防科技大学学报, 2014, 36(6): 18-24.

[19]Wang D, Wu Z, Fei Y, et al. Structural design employing a sequential approximation optimization approach[J]. Computers & Structures, 2014, 134: 75-87.

(编辑：崔贤彬)

Surrogate based grain design optimization for solid rocket motor

WU Ze-ping, WANG Dong-hui, HU Fan, ZHANG Wei-hua

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha410073, China)

An optimization design method for solid rockot motor grain based on surrogate model was proposed. To enhance the efficiency of surrogate based SRM grain design, a Pareto front based parallel infill criteria was proposed. Taking a finocyl grain design as an example, the variance of the thrust was minimized and a smooth thrust-time curve was obtained, which proves the effectiveness of the method.

solid rocket motor；surrogate model；parallel infill criteria；design optimization method；LevelSet；grain design

2015-04-20；

2015-06-15。

武泽平(1990—)，男，博士生，研究方向为飞行器总体设计。E-mail:zeping90315@126.com

V438

A

1006-2793(2016)03-0321-06

10.7673/j.issn.1006-2793.2016.03.005