一种改进的可并行的K-medoids聚类算法

马晓慧

（山西大学商务学院，太原　030031）

一种改进的可并行的K-medoids聚类算法

马晓慧

（山西大学商务学院，太原030031）

针对K-medoids算法中初始聚类中心的结点的选取的随机性导致影响聚类结果质量的问题，采用标签共现原则对该算法进行改进。根据标签共现频率和相似度先对标签进行聚类，根据标签聚类结果，选取K个由其代表的资源作为聚类初始中心结点。通过聚类中心的优化设置，降低了抽样选取的随机性。最后采用MapReduce框架对其进行并行化，以豆瓣图书的标签数据为应用背景进行实验，验证了算法的实用性。

MapReduce；K-medoids；Hadoop

0　引 言

随着大数据时代的来临，相伴而生的信息技术、云计算等技术的蓬勃兴起，从海量的数据中精准高效地提取挖掘出有用的信息，即已成为倍受各方瞩目和关注的一个热点课题［1-2］。聚类是一种无监督的学习过程，可将给定数据集合划分成若干个簇，以簇内数据相似度高，簇间相似度低为聚类目标。自聚类概念提出以来，已经产生了诸如划分聚类、谱聚类、层次聚类、模糊聚类等众多算法。其中，K均值作为经典聚类算法，则在生物信息学、图像处理、兴趣推荐等众多领域获得了广泛应用。但是，已有研究证明该聚类算法也存在一定问题，诸如聚类结果可能出现局部最优而非全局最优、迭代次数过高等。

面对复杂多变、以指数级别增长的大规模数据，传统的聚类算法已经在效率上遭遇瓶颈，存在着伸缩性与扩展性较差等问题，无法满足时下计算的性能效果要求［3］。在新的数据生产模式下，研究高端完善、适应性强的海量数据聚类算法即已突显其现实重要性。同时，针对并行计算的快速发展，在其中关于并行计算编程模型的研发提出则为问题解决提供了新的有益思路和有利支持。

1　相关背景

1.1MapReduce

Hadoop是专为分布式计算和分布式存储而设计生成的本文算法使用欧几里得距离衡量结点间距离，数学计算一个运行大规模数据的软件平台，是Apache的一个使用Java实现的开源框架。HDFS和MapReduce是Hadoop的两大核心。具体地，MapReduce是谷歌提出的一种编程模型，可以用来对海量数据调用完成并行计算。MapReduce将输入数据转成输出数据，”Map”和”Reduce”的概念来自于函数式编程语言。映射对输入的每条数据使用一个函数变换来创建一个输出列表，元数据列表不会改变。化简接受数据并聚合起来返回输出值。Map函数和Reduce函数只接收Key-Value对，而不接收整型、String型的数值。有相同键值的数值都将传入同一个Reduce函数实现自动汇总。MapReduce的工作流程如图1所示［4］。

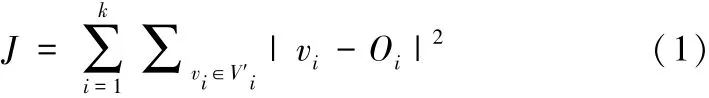
1.2一种改进的K-medoids聚类算法

K-medoids聚类算法的基本思想是，给定节点集V，V=｛v1，v2，…，vn｝为n个结点的集合，其中vi=｛vi1，vi2，vi3，…，vip｝为p维数据点，找到k个初始结点作为聚类中心，判断其他结点到各中心距离，将其分配到对应类中。得到R= V′1，V′2，…，V′K，其中∀Vi′，Vj′∈V，i≠j，Vi′∩Vj′=Ø，使得每个数据点vi（0≤i≤n）和其最近聚类中心的距离平方和J最小。此时，J可称为目标函数，数学描述可如式（1）所示。即如公式（2）所示。

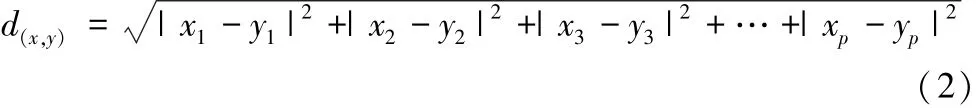
其中，x=｛x1，x2，x3，…，xp｝，y=｛y1，y2，y3，…，yp｝是集合V中的p维数据点。

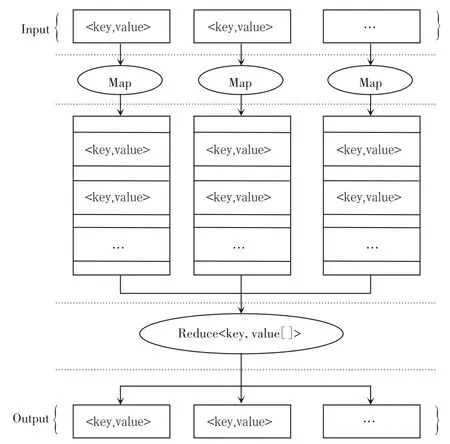
图1　MapReduce流程图Fig.1 Flow chart of MapReduce

综上研究可知，初始聚类中心的结点选取是随机的，有较大的盲目性，取值对聚类结果质量影响很大，容易导致算法陷入局部最优或分类准确率下降等问题。针对此类问题，本文拟采用标签共现原则对该算法提出设计改进。事实上，在协同标记系统中会大量出现用不同标签标记相同资源的现象，文献［5］指出如果用户使用不同标签来标记相同的资源，则标签间一定存在着语义相关性，文献［6］提出了一种基于标签共现的聚类算法来生成标签聚类簇。如果在同一个聚类中结点属性相似度高且结构紧密，不同聚类中结点属性值差异性大，则称为理想聚类效果［7］。本文提出的算法在对结点划分的过程中，应用了2个划分原则［8］。原则设定可表述如下：

原则1：如果2个结点的属性标签描述一致且同处于同一标签簇中，则2个结点应划分为同一结点簇。

原则2：如果2个结点的大部分邻居结点相同，则这2个结点应划分为同一结点簇。

在此基础上，根据标签共现频率和相似度先对标签进行聚类，根据不同的标签聚类选取K个由其代表的资源作为聚类初始中心结点。通过聚类中心的优化设置，降低了抽样选取的随机性。

定义1（共同标注矩阵） 如表1所示，Um×m是一个共同标注矩阵，fij表示标签ti和tj共同出现过的频率。频率越高，则标签ti和tj相似度就越高。

研究中，利用公式（3）来计算2个标签的共现频率，其中，w（ti，tj）代表标签ti和tj共同出现的次数。

表1　标签共同标注矩阵Um×mTab.1 Tag co-occurrence matrix Um×m

至此，本文研究提出了改进的K-medoids聚类算法1。算法内容描述如下：

算法1 改进的K-medoids聚类算法

输入：带属性标签的资源节点集，V=｛v1，v2，…，vn｝为n个结点的集合，A=｛a1，a2，…，am｝为结点vi的m个标签的集合。

输出：k个聚类结果，R=V′1，V′2，…，V′k其中，∀V′i，V′j∈V，i≠j，V′i∩V′j=Ø。

1：数据准备，标签预处理，根据公式（2）计算标签的共现频率。设定阈值，将标签划分为k个标签簇。

2：根据标签簇选择k个资源结点作为初始聚类中心，并对k个结点进行顺序编号，记做（u1，u2，…，uk）。

3：根据公式（2）计算其余数据点与选定的k个初始聚类中心的距离，并将其划分到对应的最短距离类中。

4：由公式（1），得到当前目标函数Ec[9]值。

5：在上次的聚类结果中，顺序选择一个非中心数据点，重新计算目标函数E［9］。

6：根据计算结果对类中心进行更新，得到k个新类。

7：循环执行步骤3～6，得到k个聚类结果，R=V′1，V′2，…，V′k。

8：结束。

2　基于并行框架的K-medoids聚类算法实现

对聚类算法的并行处理中，首先在HDFS上部署可以由集群中机器访问的初始化k个类中心。在K-medoids算法中，每个资源节点和类中心的距离计算过程是独立于其他资源结点的，不存在依赖关系。因此，在MapReduce框架下，各个资源节点和k个类中心距离的计算过程可以并行发生、且实现。基于这一思想，将算法1通过并行化得到算法2，并行算法描述如下。

算法2 改进的可并行的K-medoids聚类算法

输入：带属性标签的资源节点集，V=｛v1，v2，…，vn｝为n个结点的集合，A=｛a1，a2，…，am｝为结点vi的m个标签的集合。

输出：k个聚类结果，R=V′1，V′2，…，V′k。其中，∀V′i，V′j∈V，i≠j，V′i∩V′j=Ø。

1：数据准备，标签预处理，根据公式（2）计算标签的共现频率。设定阈值，将标签划分为k个标签簇。

2：根据标签簇选择k个资源结点作为初始聚类中心，并对k个结点进行顺序编号，记做（u1，u2，…，uk）。

3：Map函数将步骤2中输出的k个结点作为K-medoids的初始聚类中心，结点表示形式为＜key，value＞，value为p维属性结点形式。对于每条记录，计算和其距离最小的聚类中心并做归属新类别标记。Map的输出结果＜key，value＞形为＜聚类类别，｛属性向量｝＞。

4：Reduce函数接收Map函数的输入，将同一key值下的数据点合并，计算Key均值并将计算结果输出［10］。

5：结束。

3　实验和结果

3.1实验环境搭建

实验平台采用虚拟机形式，使用VMWare8.0.2和Ubuntu10.04，虚拟出4台设备搭建Hadoop集群。其中一台作为Master主节点（即NameNode和Job-Tracker），另外3台作为slave节点（即DataNode或Task-Tracker），Hadoop版本为1.0.3、JDK1.6，用Java实现算法。

3.2实验结果分析

如式（4）所示，加速比S是衡量并行算法性能的一个重要指标。其中，Ts为算法串行运行时间，Tp为算法并行运行时间。加速比越大，效率越高。

实验采用数据集使用Python爬取的豆瓣图书及标签数据。数据集按大小划分，DS1取5 000条，DS2取20 000条，DS3取50 000条，在这3组数据集上做聚类分析，将4个计算节点逐一加入计算，运行时间对比如表2所示，加速比测试图如图2所示。由表2和图2可看出，数据量较小时并行效果并不明显，因为小数据量的实际计算时间占比有限［11］。随着数据集规模增大，算法加速比随着节点数增加而线性增加，性能则趋于提升和完善。

图2　加速比测试结果Fig.2 Result of the speed-up ratio test

表2　算法运行时间对比Tab.2 Comparison of the algorithm’s running time

［1］刘智慧，张泉灵.大数据技术研究综述［J］.浙江大学学报（工学版），2014，48（6）：957-972.

［2］陈吉荣，乐嘉锦.基于Hadoop生态系统的大数据解决方案综述［J］.计算机工程与科学，2013，35（10）：25-35.

［3］李榴，唐九阳，葛斌，等.K-DmeansWM：一种基于P2P网络的分布式聚类算法［J］.计算机科学，2010，37（1）：39-41.

［4］刘刚.Hadoop应用开发技术详解［M］.北京：机械工业出版社，2014：130-192.

［5］MICHLMAYR E，CAYZER S.Learning user profiles from tagging data and leveraging them for personalized information access［C］// Proceedings of the Workshop on Tagging and Metadata for Social Information Organization.Banff，Canada：［S.l.］，2007：1-7.

［6］王萍，张际平.一种社会性标签聚类算法［J］.计算机应用与软件，2010，27（2）：126-129.

［7］吴烨，钟志农，熊伟，等.一种高效的属性图聚类方法［J］.计算机学报，2013，36（8）：1704-1713.

［8］RAGHAVAN U，ALBERT R，KUMARA S.Near linear time algorithm to detect community structures in large-scale networks［J］.Physical Review E，2007，76（3）：36-106.

［9］金冉.面向大规模数据的聚类算法研究及应用［D］.上海：东华大学，2015：14-20.

［10］毛典辉.基于MapReduce的Canopy-Kmeans改进算法［J］.计算机工程与应用，2012，48（27）：22-26，68.

［11］周婷，张君瑛，罗成.基于Hadoop的K-means聚类算法的实现［J］.计算机技术与发展，2013，23（7）：18-21.

An improved parallel K-medoids clustering algorithm

MA Xiaohui
（Business College，Shanxi University，Taiyuan 030031，China）

The K-medoids algorithm suffered from one problem which the quality of clustering results was sensitive to the initial cluster centers selection.The paper improves the algorithm using the principle of the tag co-occurrence.According to the tag co-occurrence frequency and similarity，clustering is carried out on the tags，and K resources are selected as the initial clustering center nodes on the basis of different tag cluster.After that，the paper reduces the randomness of sampling selection by optimizing the clustering center. Furthermore，MapReduce framework is adopted to carry out the parallel algorithm.Finally through the experiment with the application background of Douban books，the experimental result verifies the practicability of the algorithm.

MapReduce；K-medoids；Hadoop

TP391

A

2095-2163（2016）03-0100-03

2016-05-31

2014年省科技厅基础研究项目（2014011018-1）；2015年学院科研项目（2015009）。

马晓慧（1982-），女，硕士，讲师，主要研究方向：计算机应用技术、信息检索、并行算法。