矮塔斜拉桥抗弯极限承载力数值计算及验证*

胡世翔　黄侨†　刘义河

(1.东南大学 交通学院， 江苏 南京 210096； 2.吉林省交通规划设计院， 吉林 长春130021)



矮塔斜拉桥抗弯极限承载力数值计算及验证*

胡世翔1黄侨1†刘义河2

(1.东南大学 交通学院， 江苏 南京 210096； 2.吉林省交通规划设计院， 吉林 长春130021)

为研究多塔矮塔斜拉桥主梁的破坏形式和抗弯极限承载力，以宁江松花江特大桥为背景工程，采用ANSYS软件，分别基于Drucker-Prager屈服准则和Willam-Warnke五参数破坏准则建立两种三维实体有限元模型，分析结构从承受设计荷载至破坏荷载整个过程的受力状态并得到3种工况下的结构抗弯极限承载力，和现行桥梁规范(JTG D62—2004)方法的计算值进行了对比.结果表明：两种有限元模型的抗弯极限承载力计算值相对规范方法计算值的平均误差分别为2.7%和6.5%，最大误差分别为5.9%和8.6%，有限元分析结果与规范方法计算值吻合较好；结构在活载系数小于3时基本处于弹性状态；中跨跨中加载为该桥安全系数最小的工况，其安全系数为2.08.

矮塔斜拉桥; 极限承载力; 非线性分析; 屈服准则; 全过程分析

矮塔斜拉桥是一种介于连续梁桥和斜拉桥之间的桥型，近十几年来在我国得到广泛应用.与斜拉桥相比，矮塔斜拉桥主梁刚度较大，荷载主要是由主梁承担，与连续梁桥相比，矮塔斜拉桥主梁不仅承受很大弯矩作用，还存在较大的轴力，主梁是主要受力构件而且受力复杂，其极限承载能力研究是该桥型推广、应用的基础之一.

在设计中，一般按照现行桥梁规范来验算主梁截面的抗弯或者偏压承载力,规范中公式是基于构件试验推导而来，可以计算控制截面破坏时刻的承载力.与规范方法相比，文中采用的基于有限元的全过程分析方法，不仅可以根据活载系数-位移曲线得到结构极限承载力，还可以得到结构从弹性到塑性直至破坏整个过程的受力和变形，了解结构超载时的受力状态，为安全运营管理提供科学依据.

限于经费和试验条件，想通过试验来研究大型桥梁结构直至破坏的受力全过程是非常困难的，可以采用有限元方法来得到数值模拟结果[1- 3].韦成龙等[4]提出一种能够考虑混凝土桥面板和钢主桁组合作用的梁段单元，并应用于一座两塔三跨矮塔斜拉桥的极限承载力分析.郑一峰[1]基于ANSYS软件，采用四点矩形板壳单元模拟箱梁，分析了一座两塔三跨矮塔斜拉桥.吴光宇[5]基于虚拟层合单元理论，分析了一连续刚构桥各工况下的极限承载力.徐金勇等[6]基于空间薄壁梁单元，编制相应程序,分析了一座双塔三跨斜拉桥的极限承载力.

以上研究均采用梁单元或板壳单元，而采用三维实体精细有限元进行结构全过程分析的研究较少，目前主要集中在简单结构，如简支梁桥[7- 8]，应用于大型复杂结构的很少，这是因为采用精细实体有限元进行考虑非线性的全过程分析,难以实现计算收敛.文中通过选择合理的材料本构、强度准则、加载方式及收敛条件，并将结构实体部分全部划分为质量较好的六面体网格，对一座四塔五跨大型矮塔斜拉桥的主梁进行直至加载破坏的全过程分析，研究结构从弹性状态直到破坏整个过程中的内力和变形.分析时，基于不同的强度理论建立了两种有限元模型，比较了两者的结果，并将得到的极限承载力和规范方法结果进行对比，间接验证了有限元分析结果的正确性.

1　基本原理

桥梁结构的极限承载能力可以采用全过程分析方法进行研究，该方法通过逐级增加活载来分析结构的变形和受力，直至计算到结构的某一部分发生破坏为止，并将实际施加活载和设计活载的比值定义为活载系数.

进行全过程分析需要考虑结构的几何非线性和材料非线性.矮塔斜拉桥几何非线性主要来自于3个方面:斜拉索的垂度效应、结构大位移效应和梁-柱效应[9].在极限荷载作用下，结构很多区域处于高应力状态，混凝土、钢绞线等材料呈现出明显的材料非线性，选择合适的材料本构和强度准则是分析的关键[10- 12].

1.1Willam-Warnke强度准则

1.2Drucker-Prager屈服准则

Drucker-Prager屈服准则(简称D-P准则)是对Mohr-Coulomb准则(简称M-C准则)的近似[16]，M-C屈服准则可以表示为

(1)

式中，c为材料的粘聚力，φ为内摩擦角，J2为应力偏量的第二不变量，I1为应力张量的第一不变量，θσ为应力Lode角.

在主应力空间中的破坏曲面(见图1)为非正六边形锥体，由于六边形角隅部分在计算机数值计算中非常复杂，D-P准则将其修正为圆形.

图1　Drucker-Prager破坏曲面

D-P屈服准则表达式为

(2)

(3)

(4)

1.3钢材的强度准则

在有限元模型中，钢筋、预应力钢绞线和斜拉索均可采用Von Mises屈服准则[15]，其表达式为

(5)

式中，σS为单向拉伸时的屈服极限，k为常数.该准则表明当应力偏量的第二不变量达到一定值时，材料进入屈服状态.

比较式(2)和(5)，D-P准则在VonMises屈服准则的表达式中多了一个附加项，由此可以考虑静水压力的影响.和W-W准则相比，D-P准则假定材料为理想弹塑性，没有强化过程，其屈服面不随着材料的屈服而改变，适用于混凝土、岩石等材料[14].

2　有限元分析模型

2.1工程背景

宁江-松花江特大桥位于吉林省松原市，是一座四塔五跨的矮塔斜拉桥.跨径布置为95m+3×150m+95m，边跨与主跨跨径比为0.63，预应力混凝土主梁采用变截面，梁高3.0～5.5m，塔高21.5m.采用单索面—双排索的拉索布置形式，单根拉索由37根15.24mm的钢绞线构成，桥型布置及加载工况见图2.

图2　加载工况示意图(单位：m)

2.2有限元分析中的基本原则与规定

根据ANSYS的内嵌功能和结构的具体情况，本研究中的计算分析遵循下列基本原则与规定：

①文中主要研究主梁各控制截面的抗弯极限承载力，假设索梁、索塔锚固区、预应力锚固区、支座、桥墩及基础、主塔等不会先发生局部破坏.

②分析各控制截面抗弯极限承载力时仅包括下列荷载：结构自重、二期恒载、预应力、斜拉索索力和汽车活载，不考虑混凝土收缩、徐变、温度和支座变位的影响.

③根据混凝土采用的强度理论不同，分别建立了基于D-P准则和W-W准则的两种模型，模型中的材料参数、边界条件及网格划分等均相同.

④以活载系数-位移曲线作为判断结构是否达到破坏的主要依据，同时查看相应的钢材和混凝土应力状态.计算中应力以拉应力为正，主梁竖向挠度向下为正.

⑤模型加载方式为力加载，采用位移收敛准则，收敛精度为2.5%，在结构接近破坏时为了加快收敛放宽到5%.

2.3模型介绍

根据结构的横向对称性，文中建立了半结构的有限元模型(如图3所示).结构中主梁、索塔均采用SOLID65实体单元，4个桥墩中，11#桥墩和主梁固结，采用SOLID65实体单元，其他3个桥墩处主梁支撑在墩顶支座上，故仅采用SOLID45实体单元建立支座，没有建出桥墩.为提高计算收敛性，实体单元全部划分为质量较好的六面体网格，其中主梁单元横截面尺寸约为30 cm×30 cm，纵向约为100 cm，索塔和桥墩单元横截面尺寸约为30 cm×100 cm，竖向约为100 cm.预应力筋采用分离式建模方法，将预应力钢筋和混凝土分别建模，采用共节点的方式连接，并认为混凝土和钢筋之间黏结良好，不考虑两者之间的滑移.桥梁横向和竖向普通钢筋采用

图3　半幅桥梁有限元模型

配筋率的方式模拟.模型中边界条件为：11#桥墩的底面为固结约束，其他3个桥墩处的支座底面固结，支座和主梁之间采用位移耦合方程进行约束，和结构设计一致，支座起竖向支撑的作用，释放纵桥向的水平约束和绕横桥向的转动约束.

本模型中，混凝土采用SOLID65实体单元，共计91 104个；梁支座采用SOLID45实体单元模拟，共计300个；预应力钢筋和斜拉索采用LINK8杆单元，共计360 676个.混凝土采用E.Hognestad本构模型，钢绞线采用双折线模型，材料参数见表1.

表1　主要材料参数

2.4加载工况

文中在进行极限承载力分析时，只考虑恒载和汽车活载共同作用.汽车活载采用公路Ⅰ级并按6车道计算，横向折减系数为0.55，冲击系数为1.05.

表2　有限元分析时的加载工况

为提高收敛性并加快非线性计算速度，模型中截面最不利荷载布置时，忽略了隔跨同号影响线加载的影响.根据各自影响线的面积计算可知，各截面内力分别为考虑隔跨加载的88%、96%和95%.为了便于与规范计算结果作对比，有限元计算结果均为考虑上述折减系数后的数值.

3　基于有限元的分析结果

3.1工况Ⅰ加载的计算结果

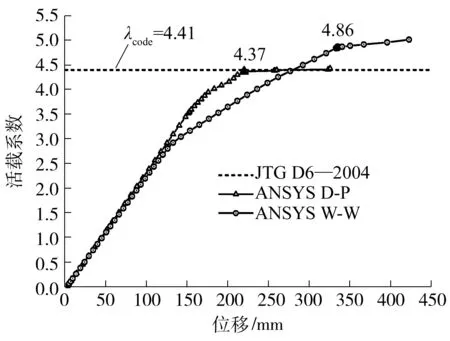
图4　截面A的-f曲线

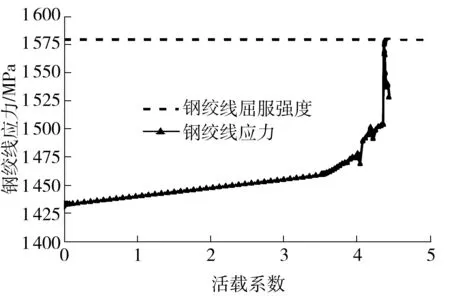
图5　截面A位置处的受拉区钢绞线应力(D-P准则)

Fig.5Stress of steel strand in tensile region of section A(D-P criterion)

图6结构破坏时截面A受压区混凝土纵向应力分布(D-P准则)

Fig.6Longitudinal stress of main girder top slab under ultimate load in section A(D-P criterion)

图7　截面A位置处的受拉区钢绞线应力(W-W准则)

Fig.7Stress of steel strand in tensile region of section A(W-W criterion)

图8结构破坏时截面A受压区混凝土纵向应力分布(W-W准则)

Fig.8Longitudinal stress of main girder top slab under ultimate load in section A(W-W criterion)

3.2工况Ⅱ加载的计算结果

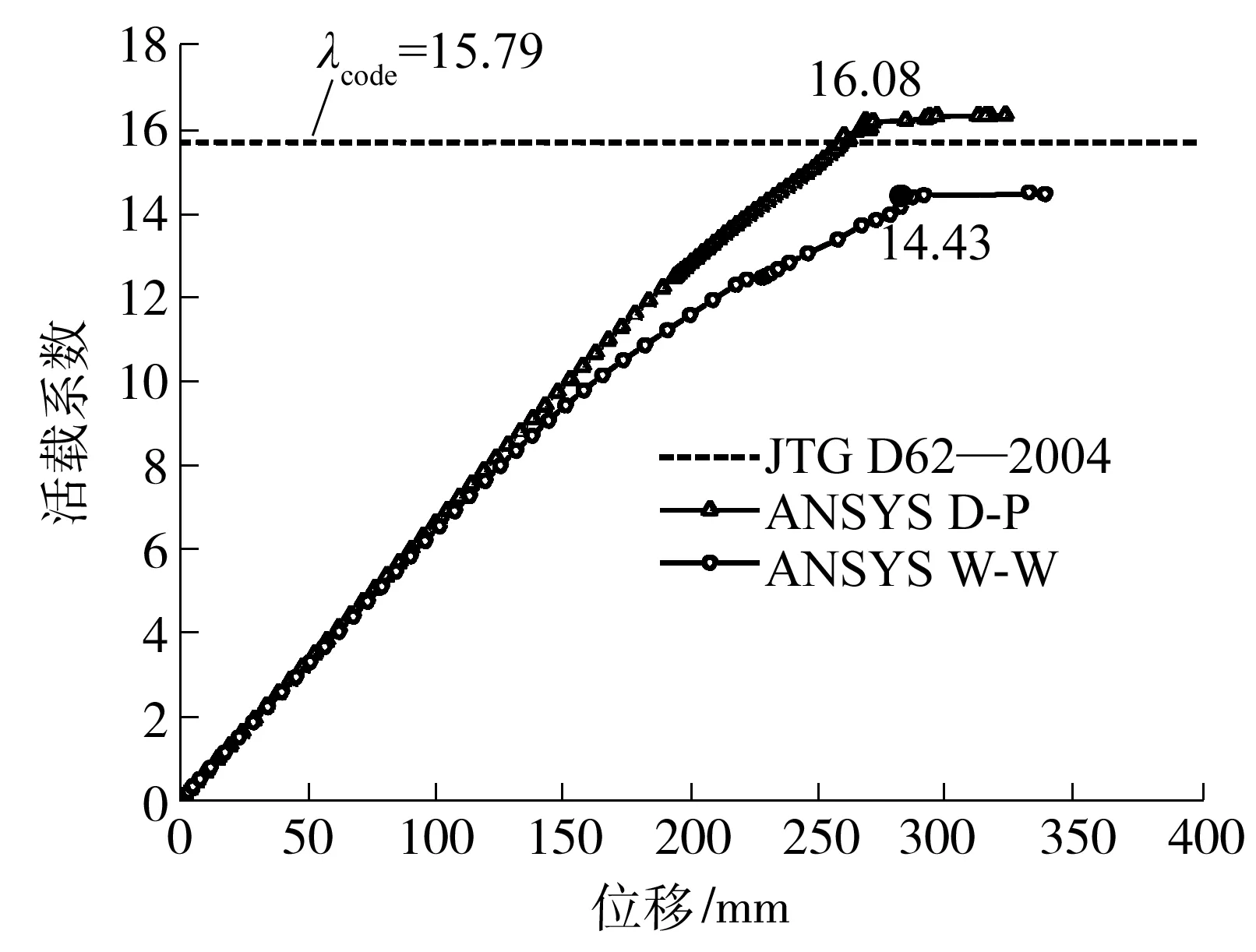
图9　P2位置的-f曲线

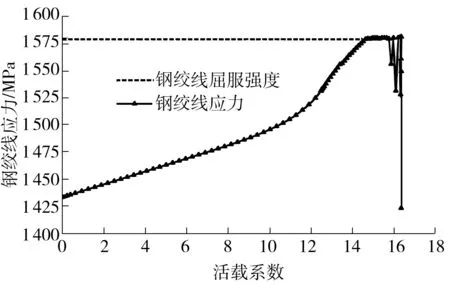
图10　截面B上缘受拉区钢绞线应力(D-P准则)

Fig.10Stress of steel strand in tensile region of section B(D-P criterion)

图11结构破坏时截面B受压区混凝土纵向应力分布(D-P准则)

Fig.11Longitudinal stress of main girder top slab under ultimate load in section B(D-P criterion)

图12　截面B受拉区钢绞线应力(W-W准则)

Fig.12Stress of steel strand in tensile region of section B(W-W criterion)

图13结构破坏时截面B受压区混凝土纵向应力分布(W-W准则)

Fig.13Longitudinal stress of main girder top slab under ultimate load in section B(W-W criterion)

3.3工况Ⅲ加载的计算结果

工况Ⅲ加载时截面C为破坏截面，结构仅主墩处存在纵向水平约束，故处于无索区的截面C中无轴力，其破坏形式为正截面受弯破坏.

两个模型的工况Ⅲ加载时，由于破坏截面仅受弯矩作用，两种有限元模型的结果更加接近，两条

图14　截面C的-f曲线

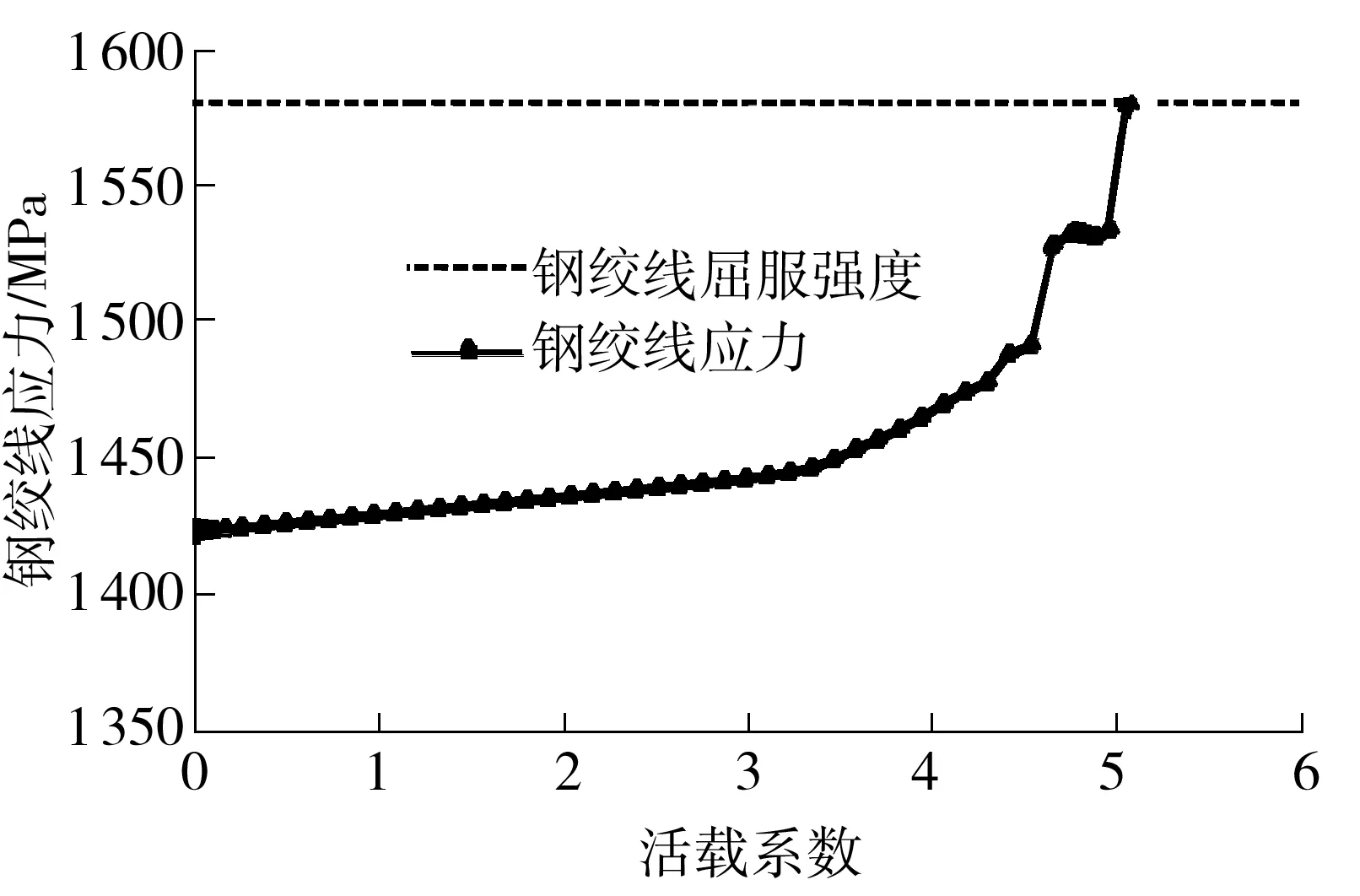
图15　截面C受拉区钢绞线应力(D-P准则)

Fig.15Stress of steel strand in tensile region of section C(D-P criterion)

图16结构破坏时截面C受压区混凝土纵向应力分布(D-P准则)

Fig.16Longitudinal stress of main girder top slab under ultimate load in section C(D-P criterion)

图17　截面C受拉区钢绞线应力(W-W准则)

Fig.17Stress of steel strand in tensile region of section C(W-W criterion)

图18结构破坏时截面C受压区混凝土纵向应力分布(W-W准则)

Fig.18Longitudinal stress of main girder top slab under ultimate load in section C(W-W criterion)

3.4有限元计算结果总结

在各工况的承载能力极限状态下，斜拉索的最大索力分布在975.5～1 327.5 MPa，均小于其屈服强度1 580 MPa.

工况Ⅰ和工况Ⅲ加载时，破坏截面受正弯矩作用，在活载系数小于3时，两个工况的荷载-位移曲线都基本为直线，结构处于弹性状态.工况Ⅱ加载时，破坏截面受负弯矩作用，截面承载力富余较大，活载系数小于10时，结构基本处于弹性状态.

4　基于规范方法的计算结果

在无法进行破坏试验的情况下，文中采用规范方法间接验证有限元数值分析的正确性.可以根据JTG D62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》计算截面A、B和C的极限承载力，计算时不计材料安全系数、荷载安全系数及其组合系数，加载工况按照表3和图2布置，与有限元计算不同的是考虑了隔跨加载.和有限元分析一致，计算内力时仅考虑结构的自重、恒载、索力、预应力及计入冲击系数的汽车荷载.具体计算过程见图19所示的流程，计算结果见表4，其中k为根据式(6)计算的抗弯承载能力安全系数.

表3　规范方法计算时的加载工况

图19　截面极限承载力计算流程图

Fig.19Flowchart for analyzing the ultimate bearing capacity of bridge

表4基于规范方法的各工况极限承载力计算结果汇总

Table 4Calculated ultimate load in differeat caves obtained by the bridge code method

工况破坏截面规范方法计算值codeM1)U/(kN·m)NU/kNkⅠA4.41272321.016463.52.93ⅡB15.791334413.0128929.56.78ⅢC5.54410772.1—2.21

1)MU为截面按照相应工况加载时能承受的最大弯矩.

5　3种方法的抗弯极限承载力计算结果对比

为了分析结构承载能力富余程度，定义结构抗弯承载能力安全系数k为

(6)

(7)

文中采用了3种方法分析主梁抗弯极限承载力，其中规范方法可以得到截面破坏时刻的承载力，两种有限元方法不仅可以根据加载时的荷载-位移曲线得到结构破坏时刻的极限承载力，还可以分析结构从弹性到塑性直到破坏整个受力过程.3种方法的分析计算结果见表4-6，表5和6中的误差是指相对于规范方法计算值的误差.

由表5可知，基于D-P准则的极限抗弯承载力相对规范方法计算值的误差范围为-5.9%～1.7%，平均误差2.7%；由表6可知，基于W-W准则的极限抗弯承载力相对规范方法计算值的误差范围为-2.9%～8.6%，平均误差6.5%.两种有限元分析结果和规范计算值均较为接近，其中，与基于W-W准则的模型相比，基于D-P准则的计算结果更接近公路桥梁规范计算值.

表5基于D-P准则计算的各工况极限承载力计算结果汇总

Table 5Calculated ultimate load in different cases obtained by the D-P yield criteria

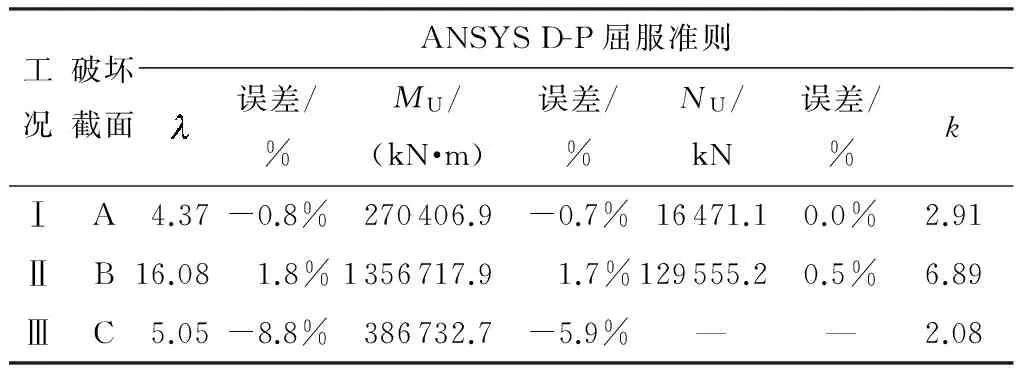
工况破坏截面ANSYSD-P屈服准则误差/%MU/(kN·m)误差/%NU/kN误差/%kⅠA4.37-0.8%270406.9-0.7%16471.10.0%2.91ⅡB16.081.8%1356717.91.7%129555.20.5%6.89ⅢC5.05-8.8%386732.7-5.9%——2.08

表6　基于W-W准则计算的各工况极限承载力计算结果汇总Table 6　Calculated ultimate load in differeat cases obtained by the W-W yield criteria

根据表4-6，如果偏安全地取每种方法的最小值，结构达到承载能力极限状态时3种工况的截面承载力安全系数分别为2.91、6.25和2.08，工况Ⅲ时安全系数最小，略大于桥梁设计规范中取用的混凝土及钢筋的材料平均安全系数1.35与恒、活载的荷载组合分项安全系数平均值1.33以及桥梁结构重要性系数1.1的乘积，即1.98.

边跨跨中和中跨跨中的承载能力富余都要远小于墩顶负弯矩区，且安全系数较小，是结构设计中需要注意的薄弱部位.斜拉索由于倾角较小，承担的活载比例较小，在极限状态时，斜拉索远未达到屈服强度，结构失效主要是主梁截面的受弯或者偏压破坏，提高结构安全储备的关键是增大主梁跨中截面的承载力.

6　结论

(1) 采用三维实体单元进行全过程分析可得到结构加载时的活载系数-位移曲线，曲线分为直线段、曲线段和接近平直段3段，对应于结构的弹性、塑性和破坏3个阶段.3个加载工况下两种有限元模型的计算结果均分别非常接近，最大误差为11.2%，最小误差仅为5.0%.

(2) 工况Ⅰ和工况Ⅲ加载时，当活载系数小于3时，两个工况的荷载-位移曲线都基本为直线，结构处于弹性状态；工况Ⅱ加载时，截面承载力富余较大，活载系数小于10时，结构基本处于弹性状态.

(3) 与桥梁规范方法计算值相比，基于D-P准则的各截面抗弯极限承载力的平均误差为2.7%，最大误差为5.9%；基于W-W准则的计算结果的平均误差和最大误差分别为6.5%和8.6%.相比之下,D-P准则模型和规范方法计算值更为接近.3种方法得到的结构抗弯极限承载力计算结果较为接近，进而间接检验了有限元数值模拟结果及基于小构件试验的桥梁规范方法的正确性和可信性.

(4) 中跨跨中加载为该桥的最不利工况，其安全系数为2.08，略大于公路桥梁设计规范中要求的安全系数1.98.对应的中跨跨中截面可视为该桥的易损截面，增大其抗弯承载力是提高结构安全储备的关键.

[1]郑一峰.混凝土部分斜拉桥设计理论研究 [D].哈尔滨：哈尔滨工业大学交通学院,2005.

[2]SONG W K,KIM S E.Analysis of the overall collapse mechanism of cable-stayed bridges with different cable layouts [J].Engineering Structures,2007,29(9)：2133- 2142.

[3]CHIO G.Structural behavior and design criteria of extradosed bridges [D].Barcelona：School of Civil Engineering,Technical University of Catalonia,2000.

[4]韦成龙,曾庆元.大跨度板桁结合主梁斜拉桥 极限承载力分析 [J].中国铁道科学,2004,25(5)：138- 140.

WEI Cheng-long,ZENG Qing-yuan.Analysis of the ultimate load carrying capacity for long span cable-stayed bridge with a plate-truss composite beam [J].China Railway Science,2004,25(5)：138- 140.

[5]吴光宇.大跨PC桥梁非线性行为的分析理论及其极限承载力计算研究 [D].杭州：浙江大学建筑工程学院,2006.

[6]徐金勇,颜全胜.大跨度混合梁斜拉桥弹塑性极限承载力分析 [J].桥梁建设,2012,42(5)：44- 50.

XU Jin-yong,YAN Quan-sheng.Analysis of elasto-plastic ultimate load bearing capacity of long span hybrid girder cable-stayed bridge [J].Bridge Construction,2012,42(5)：44- 50.

[7]刘小燕,颜东煌,张峰,等.高强混凝土 T 型梁极限承载力计算与参数分析 [J].中国铁道科学,2006,27(1)：8- 12.

LIU Xiao-yan,YAN Dong-huang,ZHANG Feng,et al.The ultimate bearing capacity and parameter analysis of high-strength concrete T-beam [J].China Railway Science,2006,27(1)：8- 12.

[8]李义强,彭正中,王新敏.基于 ANSYS 的钢筋混凝土简支梁极限承载力分析 [J].石家庄铁道学院学报,2006,19(1)：22- 26.

LI Yi-qiang,PENG Zheng-zhong,WANG Xin-min.Ultimate carrying capacity analysis of reinforced concrete simply supported beam based on ANSYS [J].Journal of Shijiazhuang Railway Institute,2006,19(1)：22- 26.

[9]OTSUKA H,WAKASA T,OGATA J,et al.Comparison of structural character-istics for different types of cable-supported prestressed concrete bridges [J].Structural Concrete,2002,3(1)：3- 21.

[10]MAHBOUBI A,AJORLOO A.Experimental study of the mechanical behavior of plastic concrete in triaxial compression [J].Cement and Concrete Research,2005,35(2)：412- 419.

[11]NAZMY A S,ABDEL-GHAFFAR A M.Three-dimensional nonlinear static analysis of cable-stayed bridges [J].Computers & Structures,1990,34(2)：257- 271.

[12]张剑,叶见曙,余波.基于Ottosen准则的PC多梁式梁桥全过程分析 [J].华南理工大学学报(自然科学版),2009,37(9)：24- 29.

ZHANG Jian,YE Jian-shu,YU Bo.Whole-process ana-lysis of PC multi-girder bridge based on Ottosen’s criterion [J].Journal of South China University of Technology(Natural Science Edition),2009,37(9)：24- 29.

[13]KLEMCZAK B.Adapting of the Willam-Warnke failure criteria for young concrete [J].Archives of Civil Engineering,2007,53(2)：323- 339.

[14]WOLANSKI A J.Flexural behavior of reinforced and prestressed concrete beams using finite element analysis [D].Milwaukee：Faculty of the Graduate School,Marquette University,2004.

[15]江见鲸,陆新征,叶列平.混凝土结构有限元分析 [M].北京：清华大学出版社,2005：44- 63.

[16]YU Tao,TENG Jin-guang,WONG Yu-long,et al.Finite element modeling of confined concrete-I：Drucker-Prager type plasticity model [J].Engineering Structures,2010,32(3)：665- 679.

Supported by the National Natural Science Foundation of China(51208096)

Validation and Numerical Calculation of Ultimate Bending Bearing Capacity of Extra-Dosed Bridges

HUShi-xiang1HUANGQiao1LIUYi-he2

(1.School of Transportation, Southeast University, Nanjing 210096, Jiangsu, China; 2.Jilin Communication Planning and Design Institute, Changchun 130021, Jilin, China)

In order to investigate the failure modes and ultimate bearing capacity of the beam of multi-span extra-dosed bridges, by using ANSYS, two three-dimensional solid element models of the Ningjiang Songhua River Bridge are constructed respectively based on the five-parameter Willam-Warnke yield criteria and the Drucker-Prager yield criteria. Then, the entire load range of the bridge, which is from a design load to a failure load, is analyzed respectively by using the two models. Moreover, the corresponding ultimate bending bearing capacities for the two models under three kinds of conditions are obtained and are compared with the calculated values based on the current bridge code (JTG D62—2004). The results show that (1) the average errors between the ultimate bearing capacities of the two finite element models and the bridge code results are respectively 2.7% and 6.5%, and the corresponding maximum errors are 5.9% and 8.6%, which means that the results based on the two finite element mo-dels accord well with the bridge code results; (2) the structure works at the elastic state when the ratio of the load to the designed live load is less than 3; and (3) the structure with the load on its midspan is of a minimum load safety factor of 2.08.

extra-dosed bridge; ultimate bearing capacity; nonlinear analysis; yield criteria; full-range analysis

2015- 10- 25

国家自然科学基金资助项目(51208096)

胡世翔(1986-),男,博士生,主要从事大跨桥梁计算理论研究.E-mail：hqhsx@163.com

黄侨(1958-),男,教授,博士生导师,主要从事大跨桥梁结构研究.E-mail：qhuanghit@126.com

1000- 565X(2016)08- 0114- 09

U 441+.4

10.3969/j.issn.1000-565X.2016.08.017