“应用数对确定位置”学习体验案例探讨
2016-11-01潘小明曾小平
尹 侠 潘小明 曾小平
(1.余庆县实验小学, 贵州 余庆 564400;2.宝山区教师进修学院, 上海 201900;3.首都师范大学初等教育学院, 北京 100048)
“应用数对确定位置”学习体验案例探讨
尹 侠1潘小明2曾小平3
(1.余庆县实验小学, 贵州 余庆 564400;2.宝山区教师进修学院, 上海 201900;3.首都师范大学初等教育学院, 北京 100048)
学生在教师的引导下,借助数形结合的思想,经历确定点的位置的探究过程。学生以一维“数射线”上确定点的位置为基础,拓展到二维平面确定点的位置,经历了直角坐标系的再发现过程。
数学化;学习体验;直角坐标系
一、教学设计
1.教学内容
人教版数学五年级上册第19页:应用数对确定物体(点)的位置。
2.教学目标
(1)结合具体情境,帮助学生掌握应用数对确定物体(点)的位置;
(2)让学生经历从“带刻度的射线”(一维空间)用“数”确定点的位置到探索平面(二维空间)上用“数对”确定物体(点)位置的发现过程,初步感知直角坐标系的形成过程。
核心素养:数形结合思想。
3.重、难点与核心问题
重点:根据具体情境,应用数对确定点的位置。
难点:理解位置(点)与数对表示的有序性、对应性、唯一性。
核心问题:怎样在平面上确定点的位置?
4.教学设计思路
学生经历从一维空间到二位空间确定位置的探究活动过程,体验数学思考与数形结合的魅力。利用学生已有的生活体验和知识基础,引入在一维的数射线上用一个“数”可确定点的位置——在二维平面用一个“数对”确定点的位置(正整数,第一象限)——初步建构平面直角坐标系——初步感悟在平面直角坐标系中四个象限中的点可用数对表示的有序性、唯一性。
二、教学过程
1.片段一:确定课题,提问质疑
教师直接出示课题:确定位置。
师:看到这课题,你想提出什么问题?
生:什么是确定位置?
生:怎样确定位置呀?
生:位置在哪里呀?
生:确定什么的位置?
生:确定位置以后,能对我们有什么帮助?
生:为什么要确定位置?
评析:美国教育家布鲁巴克认为:“最精湛的教学艺术,遵循的最高准则,就是学生自己提出问题。”教师引导学生提出问题、梳理、归类问题,既培养学生的问题意识,又可激发学生的学习兴趣[2]。
2.片断二:抓准核心,问题聚焦
师:确定谁的位置呢?
教师课件出示数射线,逐一出示下面各点(如图1),学生尝试用数确定各点的位置。

图1
在学生分别用数1、1.5、4、7 等表示出各点位置后,追问——
师:还要继续下去吗?
生1:不要了。因为任意给出一个点,都可用1个数来确定它的位置。
师:任意一个点,都可用1个数来表示出它的位置。是吗?
生2:那如果不在数射线上的点,位置该怎么确定呢?
结合生2所提问题,教师在数射线的上面给出一个点(如图2)。

(图 2)
评析:数射线上点的位置用1个数来表示,这是学生已知的;平面内点的位置怎样用数来表示,这是学生未知的。从确定数射线上点的位置到确定平面上点的位置,原有的方法不能解决当前的问题,需要实现由一维空间向二维空间思维的突破,创造出新的方法——用平面直角坐标系来确定点的位置。对于学生认知实际,是一个触及数学知识本质且极具挑战、富有创造的真问题,是本节课的核心问题。教师通过追问学生“还要继续下去吗?”引发学生深入思考。在学生想来,任意给出一个点都可以用1个数来确定它的位置,正是“任意”一词,又让学生展开联想和空间想象,提出“如果不在数射线上的点,位置该怎么确定呢?”激发学生主动探究如何确定平面内点的位置。
师:如何确定数射线上面这个点的位置呢?
生1:可以用数4来确定。
师:同意的,举手——
许多学生举手。
师:理由呢?
生1:可以用直尺对着点的位置,看看是不是与4 对齐。
师:因为这点与4对齐,所以它的位置也可以用数4来表示。这种想法,大家有不同意见吗?
生2:我觉得,毕竟是两个不同位置的点,不能用同一个数来表示。
生3:如果这个点也用数4来表示,那4到底是指哪个点呢?
生1:那这个点的位置怎么确定呢?
生4:在4的上面。
师:哎,这样就与下面的点区分开来了。
生5:在4的上面到底是几呀?
师:你为什么要问“在4的上面到底是几”?
生5:因为它只是说在4的上面,而没有说上面是几。
师:这“上面是几”,是指离开4这个点的距离吗?
生 5:是。
师:如果不说清楚这个距离,会怎么样?
生5:如果4的上面有两个点呢?
师: 噢,原来只说“ 在4的上面”,还是没法把这个点确定下来。
结合回答,教师出示图3。

图3
师:因此,刚才有人说了,还要知道在4上面的——
生:距离。
师:对呀,知道了这个距离,那就可以确定点的位置了。
评析:学生总是基于已有的知识经验去尝试解决新问题。数射线上面一点的位置,学生也试图用1个数来确定:这个数就应该是该点正对着的数射线上的那个数,绝大多数学生都同意“4”。也正是这个“4”,引发了学生“质疑——探究——再质疑——再探究”:这个点也用4表示,4到底表示哪个点?“在4的上面”,4的上面如果有两个点呢?应该知道在4的上面的距离,怎样才能知道这个距离?通过学生自我质疑,平面上点的位置必须由横向和纵向两条数射线上的数来确定的思想,在学生的头脑中逐渐形成。这种思想,比起直接应用数对来确定的操作方法,更有价值。
师:谁有办法找出这个距离?
生1:用尺子去量一量。
师出示图4。
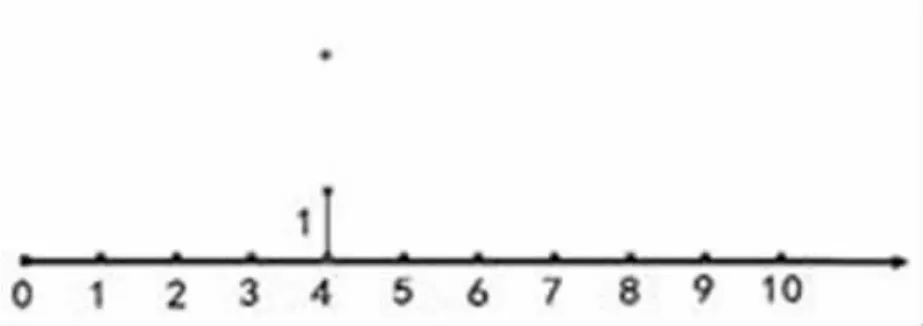
图4
师:这段距离是1。现在,这个点的位置可以怎么说?
生1:在4的上面1的地方。
师:(指着4上面第二个点)“在4的上面1的地方”,人家会不会说是这个点呢?
生:不会。
师:那要确定这个点的位置,怎么办?
生:量。
师:如果上面还有点呢?
生:再量。
师:你们的学习态度很好,不断地量下去,是吗?有没有更巧妙一点的办法?
生2:只要说4上面第几个。
师:如果点的个数有许多个,要数出第几个也是很麻烦的。
生3:可以用一把长的尺,固定在上面。
师:这样确实能解决问题,但总不能把尺一直放在上面吧。
生4:在4这里竖着向上画一条数射线。
师出示图5。

(图 5)
师:(指着点)这点的位置是——
生4:在4上面3的地方。
师:(指着上图)这条纵向的数射线画在这儿,好吗?
生:好。
师:肯定?
生5:(指着数射线上除4之外的数)如果点在这些数的上面,怎么办?
师:那就向上再画几条数射线,是吗?
生6:不是。
师:为什么?
生6:画一条就够了,只要横着对过来看一看就行了。
生7:画在0那里简便一点,那样看得清楚。
师:小朋友们在考虑看得清楚,而我首先在思考是否正确。这样画纵向数射线,正确吗?
沉默。渐渐地,有学生举手。
生8:纵向数射线的起点是从4开始的,变成4—1—2—3—4—5……也应该从0开始。
师:对呀,起点是0。数射线是从0开始, 接着是1、2、3、4等这样等距离地画下去……
师出示图6:

(图6)
评析:从多数学生的理解来看,画出纵向数射线就能知道向上的距离,也就能确定点的位置。因此,教师以“这条纵向的数射线画在这儿,好吗?”的提问,学生的回答自然说好。而平面直角坐标系是由平面上两条互相垂直且有公共原点的数轴构成,学生想的“好”显然有问题,但学生又很难自己发现。此时,教师对“数射线的起点在哪里”的提问,引发学生思考:纵向数射线上的刻度(4—1—2—3—4—5……)有问题,应将数射线由横轴上的4处移到0处,使横向、纵向数射线的起点重合。
3.片断三:抽象建模,发展思维
师:现在,将屏幕上的这个点,在方格图上画出来(师出示图7)。
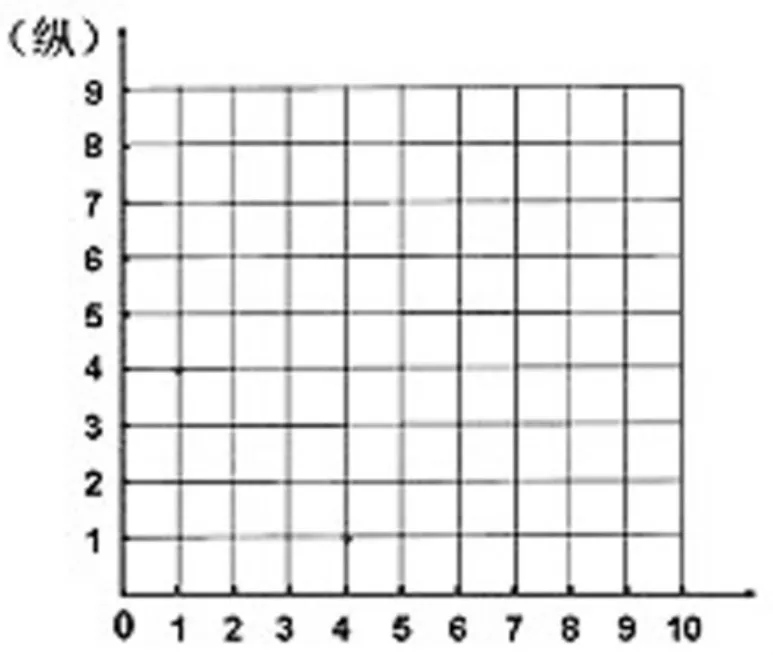
图7
师:能清楚地看出点A的位置在哪里吗?
生1:4上面1的地方。
师:4上面1的地方,这句话的确能把这点的位置给确定。但是,数学语言是非常简洁的。
生 2:横 4 纵 1。
师:能再简单些吗?
生 3:4,1。
师:对!还要加括号。读作:数对四一。
板书:(4,1)。
师:除用数对(4,1)表示外,你觉得还能怎样表示?
生 3:数对(1,4)。
板书:(1,4)。
师:你是怎么想的?
生3:先看纵轴对的是1,再看横轴对的是4,所以是数对(1,4)。
师:可以吗?
生:可以。
师:两种写法都可以,是吗?
学生小组讨论后……
生4:那点B怎么用数对表示?也是(4,1)或(1,4)都可以吗?这样,到底指点A还是点B呢?
师:问得好!为了防止混淆、确保唯一,用数对确定位置必须有个次序。数学上已经作了明确的规定——先横后纵。
师:点A的位置是——
生 5:数对(4,1)。
师:点B的位置是——
生 5:数对(1,4)。
(评析:“点 A 的位置,除用数对(4,1)表示外,你觉得还能怎样表示?”教师这是明知故问:明知只有一种表示方法却问还能怎样表示。为什么?因为有些学生想来,数对(4,1)是按先看横轴后看纵轴上的数记下的,当然也可以按照先看纵轴后看横轴上的数记下,表示的是同一个点。所以,两种方法都可以。学生的这一想法,潜藏着思维上的一个“漏洞”。教师的明知故问,问出了学生思维上的“漏洞”,为学生发现问题提供了机会。通过用事实质疑,学生更深刻地体会到有序数对确定位置的唯一性。)
之后,学生根据给出的数对(5,3)、(3,5)、(0,5),很快表示出这些点的位置。教师出示了(x,4)。学生被难住了。渐渐地,学生小声地交流着。终于,有学生走上前来。
生 1:(0,4)、(1,4)、(2,4)、(3,4)、(4,4)、(5,4)等点都有可能。
师:为什么呀?
生1:因为x可以表示任何一个数。
师:[指着(1.5,4)]这地方的点可以吗?
生1:可以。
师:x 既然表示任何一个数,那这条线上的任何一点都有可能。如果规定x 表示整数, 有可能的点一共有几个?
学生齐答:共有11个点。
生2:不止,因为数射线可以无限延长。
接着,在屏幕的右上角显示出一点(如图8)。

图8
师:有办法确定它的位置吗?
生1:把方格画出去,总能确定它的位置。
师:看来,平面上的任何一点,我们都可以用数对来确定它的位置。谁有办法给一个点,人家没办法表示的?
生1:可以把这个点画在0的后面。
师:你们知道它想画在哪里吗?
这时,在屏幕的左下角出现一点。
师:这地方的点的位置,你能确定吗?
生1:格子画大一点。
师:你把格子画大点,我就把点再放下一点,怎么办?
生2:延长。
该生在屏幕上进行延长的演示,想到用负数来确定(屏幕显示图9)。

图9
师:现在,还有哪个位置的点不能用数对来确定?
教师故意指在这儿(第二象限)、那儿(第四象限)的点,学生发现都可以用数对来确定它们的位置。
师:你真了不起!经你这么一延长, 平面内任何一点的位置都可以用数对来确定了。你叫什么名字?
生:杨某某。
师:不是吧?我记得发明这种方法的人叫———笛卡儿。
此时,屏幕出示“笛卡儿平面直角坐标系”的介绍。学生会意地笑着。
教师接着出示教材练习图,学生很快完成。
最后,教师引导学生回应课开始时提出的三个问题,(前面未突出这三个问题!)并告诉学生:用数对确定位置,不仅可以解决生活中诸如公园景点位置的确定等问题,更重要的价值是为今后的数学学习打下了基础。
三、学习体验
1.拓展教材空间,促进学生思维飞跃
如果说教材编写中以“座位”作为数对教学普遍采用的“通识”情境,仅以“先横后纵”表示“数对”在形式上完成思维浅显的教学,并未达到在学生思维深处建立“直角坐标”这一数学本质。因此,以切合学生认知实际的一维的数射线作为数学“生活化”情境,自然过渡的二维平面“数学化”的“真情境”,朴素而有深度,将数对确定位置(点)的有序性、对应性、唯一性,学生在经历这一数学知识“再发现”过程中留下深刻的个性体验。数学生活化不仅包含着“生活化”,还包含着“数学化”,数学生活化的教学不仅让学生感受到数学有用,而且学生通过现实问题的“水平数学化”和“垂直数学化”过程[1],从“一维”到“二维”空间确定位置,这是思维的飞跃,既可让学生深切感悟数学的思想和方法,又让学生在探究中促进创新能力的培养。
2.聚焦核心问题,促进探究能力培养
数学“情境一问题”教学模式实践研究认为:设置数学情境是前提,提出数学问题是核心,解决数学问题是目标,应用数学知识是归宿[2]。每节课教学,应围绕课时核心问题展开。课时核心问题是基于课时核心知识和学生认知水平、关注数学核心素养培养、统领课堂教学的重点问题。在片断二中,教师提出:“那如果不在数射线上的点,位置该怎么确定呢?”作为核心问题的聚焦,问出了学生思维中潜在的疑惑,激发学生主动探究“如何确定平面内点的位置”。教师后面的预设顺应了学生思维,首先将出示的点描述为“在4的上面”——逐渐准确表示数对(4,1)——怎样确定纵轴——引出直角坐标。一系列教学进程的展开,目的为核心问题服务。教学中抓准了课时核心问题,使课的设计和教学有“魂”、有“神”、有“味”,促进学生探究能力的培养。
3.提升思维品质,促进学生认知深化
数学活动经验并不仅仅是实践的经验,也不仅仅是解题的经验,更加重要的是思维的经验,是在数学活动中思考的经验[3]。数学课堂,以学生具备的数学活动经验作为课堂教学的开始,而在课堂结束时,反观课堂全程,学生的思维品质应比课的开始有所提升,即“学有所获”。以数学知识学会为“明线”,思维品质提升为“暗线”,通过学习知识来学会思考,形成智慧。本节教学中学生思维深处通过“点”与数对的对应关系,由一维的“线”拓展到二维的“面”,由正整数的第一象限扩充到四个象限,学生获得新的数学经验,看是随意,实为精致,促进学生认知深化。
4.积淀学科素养,促进核心素养培育
空间观念指对物体及其几何图形的形状、大小、位置关系及其变化建立起来的一种感知和认识,空间想象是建立空间观念的重要途径[4]。教学中借助方格图延伸逐渐构建平面直角系,初步建立起“形”与“数”理论体系的直观模型,简洁形象,赋予了“抽象与概括”、“符号与模型”、“图形与几何”等数学核心素养的培养,让这些数学思维意识逐步积淀,外显为良好的思维品质,促进核心素养培育。
[1]弗赖登塔尔.作为教育任务的数学[M].陈昌平,唐瑞芬译,上海教育出版社,1995.
[2]吕传汉,汪秉彝.论中小学“数学情境与提出问题”的教学[J].数学教育学报,2006,15(02):74-79.
[3]顾沛.数学基础教育中的“双基”如何发展为“四基”[J].数学教育学报,2012,11(01):18-20.
[4]黄翔.数学课程标准中的十个核心概念[J].数学教育学报,2012,11(4):16-19.
Learning Experience Case on Applying Coordinate to Determine Position
YUN Xia1PAN XIao-ming2ZENG Xiao-ping3
(1.Experimental Primary School of Yuqing County,Yuqing,Guizhou564400,China;2.The Teacher Study College of Baoshan Township,Shanghai 201900,China;3.College ofElementaryEducation,Capital Normal University,Beijing100048,China)
With the help of teacher,the students experience the inquiry process on applying coordinate to determine position the location ofpoints.Fromthe point on number line tothe point in flat,the students rediscoveryofthe Cartesian coordinate system.
Mathematic thing;LearningExperience;Cartesian Coordinate System
1009—0673(2016)04—0119—06
G623.5
A
2016—06—05
尹 侠(1973— ),男,贵州余庆人,余庆县实验小学小学数学特级教师,省级名师,研究方向:小学数学。
熊显萍
