赏析2016年数学高考理科卷中的创新试题*
2016-10-31何元国
●何元国
(洋县第二高级中学 陕西洋县 723300)
赏析2016年数学高考理科卷中的创新试题*
●何元国
(洋县第二高级中学陕西洋县723300)
2016年全国26个省市数学高考试题由分卷走向合卷,其亮点是立足课本命制创新试题,侧重考查学生的三基,深度考查学生综合分析、探究及解决问题的能力,适量加大了思维能力的考查,对中学数学教学具有现实的指导意义.
创新题;命制及对策;课堂教学
2016年全国26个省市数学高考试题由分卷走向合卷,试题总体特点:题型稳定,难度适中,创新适度.重点考查学生的基础知识、基本方法和基本能力,深度考查学生灵活运用数学思想方法综合分析、探究及解决问题的能力,适量加大了运算能力和逻辑思维能力的考查,又适度创新,对学生的不同思维层次进行良好区分[1].2016年的数学高考折射出合卷后高考试题的命题趋势,对中学数学教学具有现实的指导意义,值得教师及学生品味和研究.下面笔者从2016年数学高考理科卷中创新试题的命制方式及考查目的归类解析,与广大师生交流共赏.
1 从函数的图像与性质的关系命制试题
综合考查学生的识图、运算能力、估算判断能力及逻辑思维能力.
例1函数y=2x2-e|x|在[-2,2]上的图像大致为
()

A. B.

C. D.
(2016年全国数学高考理科卷第7题)
解从选项的4个图像知,当x=2时,y=8-e2,因此排除选项A,B.又当x>0时,y′=4x-ex,令y′=0,即4x-ex=0,在平面直角坐标系中作出函数y=4x和y=ex的图像,借助图像知在区间(0,1)中存在x0,使得4x0-ex0=0成立,且当0
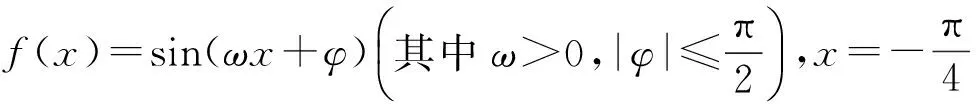
()
A.11B.9C.7D.5
(2016年全国数学高考理科Ⅰ卷第12题)





点评图像是性质的载体,性质是图像的微观刻画.命题人独具匠心,立足常规题型,但考查目的不落俗套,妙笔生花!如例1中命题人借用函数图像告知该函数的性质:可能具有奇偶性、零点、极值点(驻点)、单调性.要求学生用相关的数学手段对该函数的性质选择性探究解答.学生若识图意识不强,先由函数找图(或特殊点验证),耗时费力,得不偿失.很明显4个选项的差异有2点:1)当x=2时函数值的大小;2)当x>0时函数的单调性.学生若能抓住其差异,即可估算判断分而破之.例2命题人告知函数具有的部分性质,无图考图,让学生探究解答.学生常常会直解,虽能正确解答,但考场上时间有限,效比太低.若能抓住y=f(x)图像的特点,估算ω的最大值,回验即可求解.不过该题是选择题,直解不可取,但由大到小验证不失为有效方法.总而言之,打破惯性思维,充分利用数学思想方法跨越分析、探究研判才是破解创新试题的有效途径[2].
2 从函数图像的对称性命制试题
综合考查学生的作图、用图能力及化归与转化能力.

()
A.0B.mC.2mD.4m
(2016年全国数学高考理科Ⅱ卷第12题)


故选B.
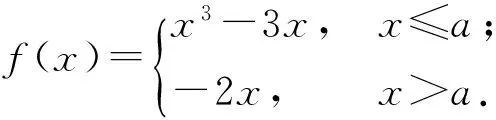
1)若a=0,则f(x)的最大值是______;
2)若f(x)无最大值,则实数a的取值范围是______.
(2016年北京市数学高考理科试题第14题)
解1)略.
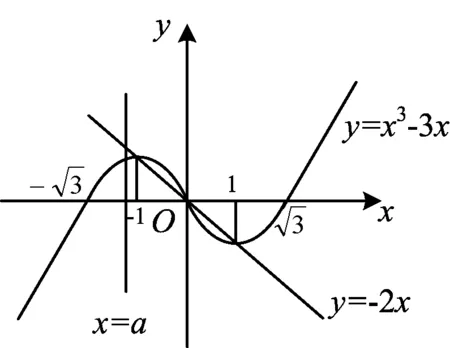
图1
2)在平面直角坐标系中作出函数y=x3-3x和y=-2x的图像(如图1所示),2个图像交点的横坐标分别是-1,0,1.
题设函数f(x)的图像是由y=x3-3x(其中x≤a)的图像与y=-2x(其中x>a)的图像组合而成,而f(x)无最大值,由图像可得实数a的取值范围是a<-1.
点评图像是性质的载体,是性质的直观再现.命题人以常规数学问题及形式,精准考查主干知识、重要方法及基本能力,含而不露.例3和例4主要考查学生作图、用图能力及数形结合能力.学生若惯性思维直解,则落入陷阱.如例3按常规运算,无济于事,迫使学生研究函数的性质,将交点坐标问题转化为交点位置问题进而数形结合求解.尤其是例4,学生粗略一看在实数集中该函数一定有最大值,怎么没有最大值?直解又感无抓手,陷入困顿.岂不知它是分段函数!分段函数的界点不仅影响其单调性、连续性,往往影响其最值的存在与否,这也是该题设计之精妙之处.当然,学生只要注意到该函数图像的构成方式,就能有惊无险,顺利解答.值得注意的是,数的问题难以解决时,不妨将数的问题转化为形的问题,形导数算可能会迎刃而解.
3 从问题的设问方式命制试题
综合考查学生阅读理解能力、逻辑思维能力及应用意识.
例5有3张卡片,分别写有1和2,1和3,2和3,甲、乙、丙3人各取走1张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数是______.
(2016年全国数学高考理科Ⅱ卷第15题)
解由丙说:“我的卡片上的数字之和不是5”出发,将甲、乙、丙3人取走卡片方案填入表1中,显然在方案②中,甲、乙相同数字是2,矛盾!故甲卡片上的数字是1和3.

表1 取卡方案
例6袋中装有偶数个球,其中红球、黑球各占一半,甲、乙、丙是3个空盒.每次从袋中任意取出2个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则
()
A.乙盒中黑球不多于丙盒中黑球
B.乙盒中红球与丙盒中黑球一样多
C.乙盒中红球不多于丙盒中红球
D.乙盒中黑球与丙盒中红球一样多
(2016年北京市数学高考理科试题第8题)
解法1(方程法)每次抓出2个球的情形有4种:①红黑;②红红;③黑黑;④黑红.
情形①会导致乙盒中黑球加1,情形②会导致乙中红球加1,情形③会导致丙中黑球加1,情形④会导致丙中红球加1.不妨设情形①~④出现的次数分别为a,b,c,d,因为红球与黑球数相同,所以
a+2b+d=a+2c+d,
即b=c,因此乙盒中的红球数等于丙盒中的黑球数.故选B.
解法2(赋值验证法)若袋中只有2个球,则放球情形如表2所示,由情形①排除选项A,由情形②排除选项D.

表2 放球情形
若袋中有4个球,则放球情形如表3所示.

表3 放球情形
由情形③可排除选项C.故选B.
点评该题打破问题设问方式惯例而创新命制试题,其目的是考查学生的阅读理解能力、化归与转化能力、抽象概括能力、探究能力和应用意识.这样的题目考查目的隐蔽,学生感到面生,找不到现成解决问题的方法,因此能更好地考查学生的思维能力.如例5,命题人改变了以往逻辑考查的常考方式如判断条件与结论的充要性、命题的否定等,取而代之的是以不同对象对问题不定判断为依据,合理推断问题,其考查的目的不变,又兼顾考查了学生的阅读理解能力、探究能力和逻辑推理能力,使人耳目一新.例6本质考查学生思维能力、方程思想和数学的应用意识,但通过命题人的巧妙包装,学生不知所措.当然,学生只要识破其表象,就能轻而易举地解决.不过从问题的设问方式上创新命制试题,包装的度要把握适中,否则就失去了试题的考查功能,这也是命题人所要规避的.
4 从学生的探究实践活动命制试题
综合考查学生探究能力、思维能力及情感态度价值观.
例7已知抛物线C:y2=2x的焦点为F,平行于x轴的2条直线l1,l2分别交C于点A,B,交C的准线于点P,Q.
1)若点F在线段AB上,R是PQ的中点,证明:AR∥FQ;
2)若△PQF的面积是△ABF面积的2倍,求AB中点的轨迹方程.
(2016年全国数学高考理科Ⅲ卷第20题)
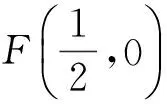


即
(a-b)(ab+1)=0.
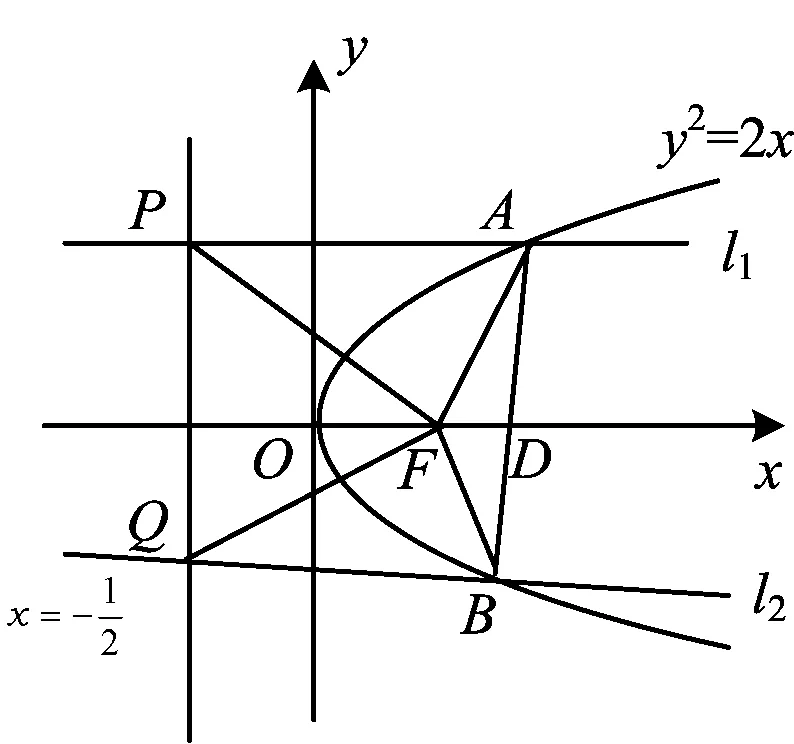
图2
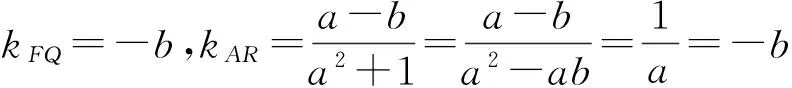
kFQ=kAR,
故
AR∥FQ.
2)如图2所示,设直线AB与x轴的交点D(x0,0),则
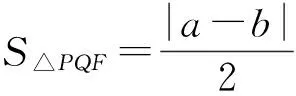

依题设可得

又a≠b且ab≠0,从而x0=0(舍去)或x0=1,因此,直线AB过定点D(1,0).
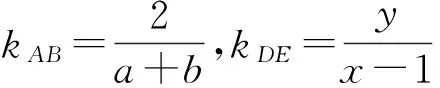


y2=x-1(其中x≠1).
当直线AB⊥x轴时,E(1,0)的坐标满足y2=x-1,故AB中点的轨迹方程为y2=x-1.
点评从学生的探究实践活动命制试题,目的是考查学生的探究能力、思维能力及情感态度价值观,综合考查学生的数学素养.例7的第2)小题考查动点轨迹方程,而动点轨迹是曲线的方程章后阅读材料及探究实践内容,新课标明确要求学生会用待定系数法求直线及标准位置圆锥曲线的方程,因此解析几何考题的第1)小题命题人常设计为求标准位置圆锥曲线的方程问题.该题中命题人打破惯例考查求动点轨迹方程,并且设计了l1,l2不与x轴重合及直线AB过定点的隐含条件,从新课标要求看确实是难题.无独有偶,2016年全国数学高考理科Ⅰ卷第12题、理科Ⅱ卷第7题均考查了三角函数图像的对称轴,而三角函数图像的对称性是教材要求学生自主探究、思考交流内容.命题人在课标与自主探究实践的接合处命制试题,其表象陈旧实则创新,对学生具有杀伤力,应引起师生的高度关注.
综上所述,2016年高考创新题,以能力立意,回避了套路题型,降低了运算量,加大了思维量,突出了对数学思想方法和能力的深度考查.命题的素材源于教材例习题(或教材例习题的变式),命题的思路从主干知识的交汇点处拼接代换、改变问题的设问方式、在课标与自主探究实践的接合处设计试题,加大了思维能力和转化与化归能力的考查,突出考查主要数学思想方法(如数形结合法、分类讨论法)[3].这就提醒我们在高三数学教学中,要回归教材,夯实数学基础知识和基本方法的训练,强化学生的思维能力、转化与化归能力和探究能力,培养学生解决问题的目标意识及数学的应用意识,理清解决问题方法的来龙去脉,摒弃轻分析重结果以及生硬地、直接地灌输式教学法,让学生经历、体验数学问题解决的全过程,培养学生思维的全面性和深刻性,这不仅有利于决胜高考,而且对学生终身发展具有深远的意义.
[1]何元国.2013年天津市数学高考理科试题难在何处[J].中学教研(数学),2013(8):46-48.
[2]徐世白.2013年浙江省《考试说明》样卷与高考真题对比分析暨2014年高考展望[J].中学教研(数学),2014(5):34-37.
[3]傅瑞琦.基于教材感悟思想导向思维——一道源于教材的中考试题命题的实践与思考[J].中学教研(数学),2015(3):41-44.
�2016-06-12;
2016-07-12
何元国(1966-)男,陕西洋县人,中学高级教师.研究方向:解题技巧与数学教育.
O12
A
1003-6407(2016)10-38-04
