提升模式层次　创新模式内涵*——2016年江苏省数学高考试题评析

2016-10-31余建国

中学教研(数学) 2016年10期

关键词：填空题考试题考点

●余建国

(大厂高级中学　江苏南京　210044)

提升模式层次创新模式内涵*
——2016年江苏省数学高考试题评析

●余建国

(大厂高级中学江苏南京210044)

2016年江苏省数学高考试题在延续“江苏模式”中求稳求变，整卷难度均衡，缓缓上升，梯度明显．除数学计算，试题在考查学生直观想象、推理论证、数学抽象、数据分析等核心素养方面都有所体现，较好地实现了区分功能，对高中数学教学有较好的导向．

高考数学；江苏卷；试题评析

江苏省从2008年开始第一次实施新课程高考，至今已有9年，是较早进入新课程改革的省份之一．江苏卷在《普通高中数学课程标准(实验)》的框架内，从考试内容、考卷形式和文理区分等方面，已形成特色鲜明的“江苏模式”．2016年江苏省数学高考试卷依然秉承自己的模式——朴实、明快、简单、延续，笔者结合自己的高三教学实践，对此谈一些粗浅的认识，不当之处请专家指正．

1　延续模式，稳中有变

江苏省数学高考试题卷Ⅰ为文理合卷，卷Ⅱ为理科附加；文科(含艺体类)数学总分160分，理科数学总分200分；卷Ⅰ只有填空题和解答题(无选择题)；卷Ⅱ“4选2”再加“2”；…等，这些都是江苏卷的特色，从2008年高考开始一直延续至今．卷Ⅰ中6个解答题的顺序几乎没有变化，第15,16题是三角函数与向量、立体几何平行和垂直证明；第17,18题是应用题、圆锥曲线；第19，20题分别是函数与导数、数列综合．

平稳的模式既反映出相应的考点(知识和方法)在高中数学中的重要性，也给一线教师的教学和备考指明了方向，但它的负面影响也逐步显现．例如，数列总是以压轴题的面目出现，对于大部分考生来说，往往只能解决第1)小题，也就是等差(比)数列的基本运算，后面的第2)和第3)小题几乎得不到分(平均分2.85).这样,在数列的学习中极易产生“滑过”现象——只教(会)一些简单的公式计算，而不教(领会)数列的思想方法[1]．笔者欣喜地看到，卷Ⅱ中第22题一改空间向量与概率分布“轮流坐庄”的模式，考查了抛物线与直线的位置关系，这样的变化提醒教师在教学和备考中不能“猜”和“压”，要在全面提升学生的思维能力和核心素养上下功夫．

2　难度均衡，拾级而上

2种题型难度均衡:填空题第1～12题以基本知识、基本方法考查为主，朴实平和，第13，14题注重考查学生的基本思维品质，难度缓缓上升，梯度明显；解答题由易到难，没有出现偏题怪题，有利于考生的正常发挥，让学生考得开心、舒心[2]．

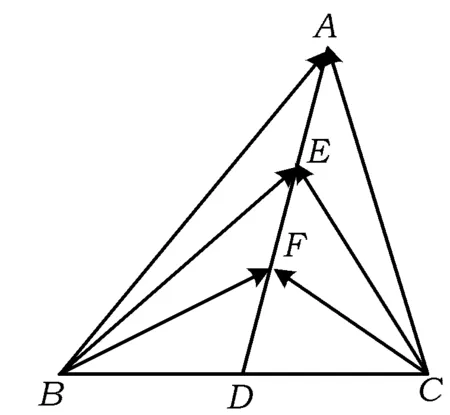
图1

(2016年江苏省数学高考试题第13题)

分析本题作为填空题压轴题之一，体现了“入口浅、寓意深”的命题主旨．从方法角度来看，考查学生对向量的2个主要方法——综合法和坐标法的掌握；从数学思想角度来看，考查学生的方程思想和转化思想；从能力角度来看，考查学生分析问题、解决问题的能力．

例2在锐角△ABC中，若sinA=2sinBsinC，则tanAtanBtanC的最小值是______．

(2016年江苏省数学高考试题第14题)

分析回顾课本，此题给考生似曾相识的亲切感．因为课本中有习题“在斜△ABC中，求证：tanAtanBtanC=tanA+tanB+tanC”，利用这个关系式，学生通过处理多变量求最值的常用方法——减元，最终用基本不等式或函数方法解决．因此，“源于课本，高于课本”也应是每位高三数学教师备考选题的策略之一．笔者提供如下解法：

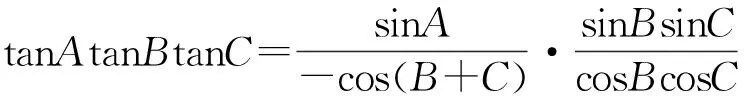
当且仅当sinBsinC-cosBcosC=cosBcosC，即sinBsinC=2cosBcosC时取到等号．

这种“整体看”能反映学生对数学知识掌握的灵活程度，抓住了基本不等式的核心——“积”与“和”的转换．因此，高三复习教学不能盲目地做题，也不能在无多大数学意义的变式上浪费时间，复习的真谛应是进一步理解数学的本质，螺旋上升，发展学生的数学思维能力．

3　控制计算，多维并举

在6个数学核心素养中，除了数学运算，还有数学抽象、逻辑推理、数学建模、直观想象、数据分析等．整卷较好地控制了运算量，多考一点想，少考一点算，在其他几个核心素养上都有所体现．第15题在三角形背景下考查同角基本关系、正弦定理、和角公式等，计算量小、途径多；第16题是立体几何题，考查直观想象、逻辑推理能力；第17题以组合体为背景，考查数学建模，背景简单易懂，导数解决方法得心应手，得分较高；第18题以圆为背景，考查解析几何基本思想——解析法，较好地回避了“一元二次方程+韦达定理”的陈旧套路．

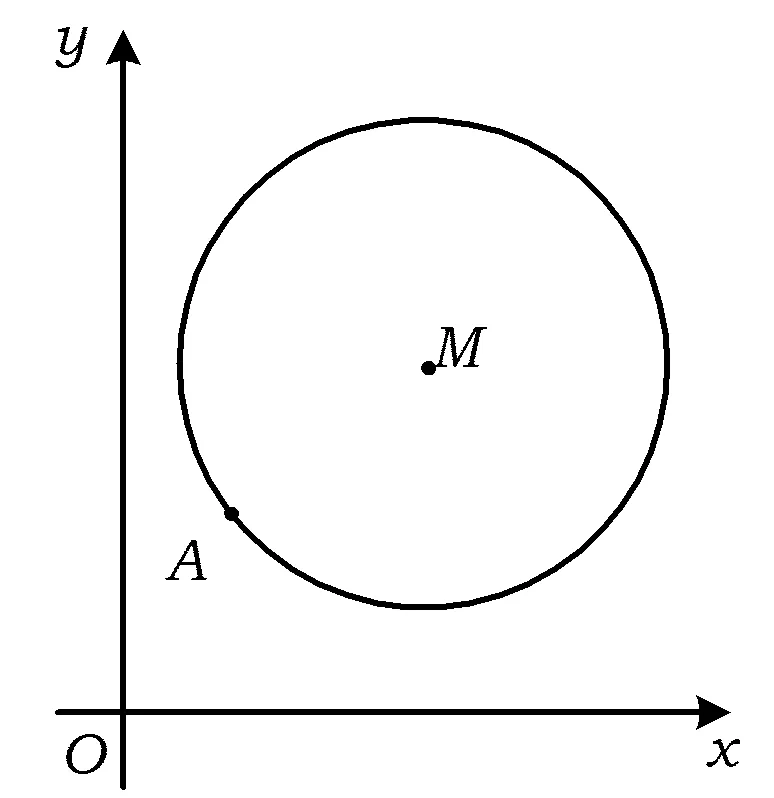
图2

例3如图2，在平面直角坐标系xOy中，已知以M为圆心的⊙M：x2+y2-12x-14y+60=0及其上一点A(2，4)．

1)设⊙N与x轴相切，与⊙M外切，且圆心N在直线x=6上，求⊙N的标准方程；

2)设平行于OA的直线l与⊙M相交于点B，C，且BC=OA，求直线l的方程；

(2016年江苏省数学高考试题第18题)

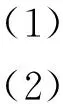
因为点Q在⊙M上，所以

(x2-6)2+(y2-7)2=25，

将式(1)和式(2)代入上式得

(x1-t-4)2+(y1-3)2=25.

此式表明，点P(x1，y1)在圆心为(t+4，3)、半径为5的⊙N上，因此⊙M与⊙N有公共点，从而

解析几何在高中阶段划分为直线与圆(必修)、圆锥曲线(选修)两大版块，它们在高中数学阶段具有同等重要的地位，解析法思想一脉相承，螺旋上升．江苏卷在卷Ⅰ中轮流考查圆或椭圆，2016年在卷Ⅰ中考查圆，而在卷Ⅱ中考查抛物线，前后呼应，相得益彰，并总是以直线与曲线的位置关系为重点，较好地渗透了数形结合思想、函数与方程思想．

4　推理论证，思维严密

试卷第19题(考查函数与导数)、第20题(数列综合)是整卷的难度“制高点”，其中第3)小题更突出，主要考查学生的推理论证能力．逻辑推理是指从一些事实和命题出发，依据逻辑规则推出一个命题的思维过程，主要包括2类:一类是从小范围成立的命题推断更大范围内成立的命题，推理形式主要有归纳、类比；一类是从大范围成立的命题推断小范围内也成立，推理形式主要有演绎推理．

例4已知函数f(x)=ax+bx(其中a>0，a≠1，b>0，b≠1)．

①求方程f(x)=2的根；

②若对于任意x∈R，不等式f(2x)≥mf(x)-6恒成立，求实数m的最大值.

2)若01，函数g(x)=f(x)-2有且只有1个零点，求ab的值．

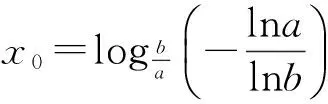
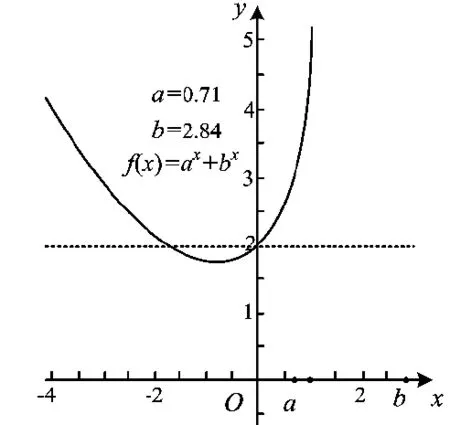
图3

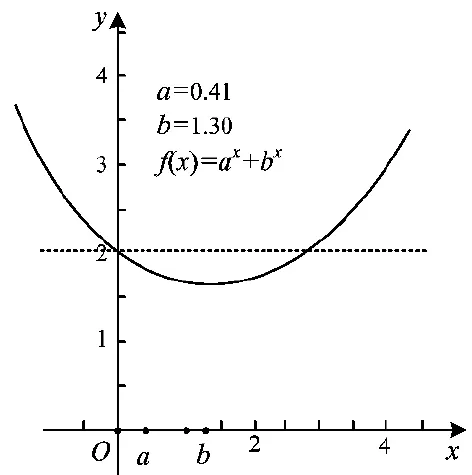
图4

所谓“不唯一”，就是能再找到一个，如何找？零点存在定理．而定理条件之一“图像连续不断”是自然的；另一个条件，也是关键所在：构造2个端点，找到零点存在的区间．从图像上发现和提出命题，基于推理的基本形式和规则，探索和表述论证的过程，这是核心素养——逻辑推理的基本要求．本题“入手容易，深人难”，较好地体现了思维层次与能力要求，有效地确保了试卷的区分度与效度，实现了高考分层选拔的功能[3].

5　外表温和，绵里藏针

试卷坚持对基本知识、基本技能及数学思想方法的考查．填空题第1～12题，解答题第15～17题基本“不设坎”，卷Ⅰ平均分为98，这也是2008年以来新课程卷中最高的．在外表温和的表象下，实则绵里藏针．

(2016年江苏省数学高考试题第12题)

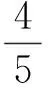
另外，第17题(应用题)选取什么为自变量，决定了目标函数的难易．一般来说，问什么设什么，这与2006年江苏卷第18题“帐篷体积”问题类似，如果设下部的正棱柱底面边长为自变量，目标函数就变得难多了．按照修改后的布鲁姆教育目标分类学[4]的说法，本题与2008年江苏卷第18题“线路总长”问题相比，稍显逊色，仅为“应用”层次，而2008年应用题为“分析”甚至“评价”层次．