多项式拟合在MEMS陀螺仪零点随机漂移抑制中的应用研究*

杜　瑾，李　杰，2*，冯凯强，刘一鸣

（1.中北大学电子测试技术国防科技重点实验室，太原030051；2.中北大学仪器科学与动态测试教育部重点实验室，太原030051）

多项式拟合在MEMS陀螺仪零点随机漂移抑制中的应用研究*

杜瑾1，李杰1，2*，冯凯强1，刘一鸣1

（1.中北大学电子测试技术国防科技重点实验室，太原030051；2.中北大学仪器科学与动态测试教育部重点实验室，太原030051）

MEMS（Micro-Electro-Mechanical Systems）传感器精度相对较低限制了其应用范围，从实际工程应用出发，针对MEMS陀螺仪零点随机漂移误差探讨了有效的补偿方法。推导了不同阶数拟合曲线的回归方程，根据实测MEMS陀螺零点数据对不同阶数拟合曲线的补偿效果进行对比，选取最优方案并通过跑车试验进行验证，证明该方法能够有效抑制陀螺仪零点漂移误差，提高微惯性导航系统的导航精度。

MEMS陀螺仪；误差补偿；最小二乘法；零点漂移

EEACC：7230doi：10.3969/j.issn.1004-1699.2016.05.018

随着MEMS技术的不断发展，基于MEMS的惯性器件由于其体积小，功耗低，可靠性高，易于集成等优点在军用和民用领域得到了广泛应用［1］，然而，由于MEMS技术属于前沿交叉学科，受到制造工艺等技术的影响，致使生产出来的陀螺仪存在零点漂移，灵敏度误差，温度漂移等难以克服的缺点［2］，只能应用于对精度要求不高的场合，这严重制约了MEMS陀螺仪发展前景。如何补偿MEMS陀螺仪零漂误差，有效提高其使用精度成为实际工程中亟待解决的难题。

本文首先对现有的MEMS陀螺误差补偿技术进行简单评述，然后通过对大量实测陀螺仪零点数据分析得出零点漂移的模型，提出基于最小二乘法多项式拟合的零位补偿的方法，进行了补偿前后MEMS陀螺仪累积角度误差输出的对比。最终通过实地跑车实验验证了该补偿方法的有效性。

1　各种补偿方法比较

对MEMS陀螺仪零漂补偿的方法按照实现条件可以分为硬件补偿和软件补偿两种。硬件补偿通常包括优化器件结构，改进工艺方法，加入电桥补偿等［3］，其优点是从根本上提高了器件的精度，但硬件补偿存在研究周期长，成本高，通用性差，调试困难等缺点，且精度提升空间有限。在计算机技术广泛应用的今天，使得对MEMS陀螺仪的零点漂移进行软件补偿变得十分方便有效。

软件补偿的基本思路是对陀螺仪的零点输出分析建模，对零漂曲线进行预测和补偿，进行试验验证补偿效果。曲线拟合的方法相对较多，常见的有BP神经网络法，插值法，最佳直线拟合，多项式拟合等［4］。神经网络具有以任意精度逼近任何非线性函数的能力，但在实用中存在收敛速度慢，目标函数易陷于局部极小点等种种问题［5］。插值法的基本思想是用高次代数多项式或分段低次多项式作为被插值函数的近似解析表达式，然而，当插值点增加或减少一个时，原来的插值多项式便不能使用，需要重新建立［6］。最小二乘法是在随机误差为正态分布时由最大似然法推出的一个最优估计技术，它可使测量误差的平方和最小因此也被视为从一组测量值中求出回归方程的最可信赖的方法。基于最小二乘法的直线与多项式拟合法计算简便，有利于计算机编程操作［7］。本文从工程实用角度出发，详细探讨最小二乘法在MEMS陀螺仪零点随机漂移误差补偿中的应用方法，为提高MEMS陀螺仪的使用精度提供一种思路和技术参考。

2　MEMS陀螺仪零漂随机误差分析与补偿

2.1数据采集与预处理

以一定的采样率对MEMS陀螺仪实际输出的连续信号进行采样，得到陀螺仪零点输出的原始数据，用滑动取平均值的方法对陀螺仪零点漂移的原始信号进行滤波，结果如图1所示。

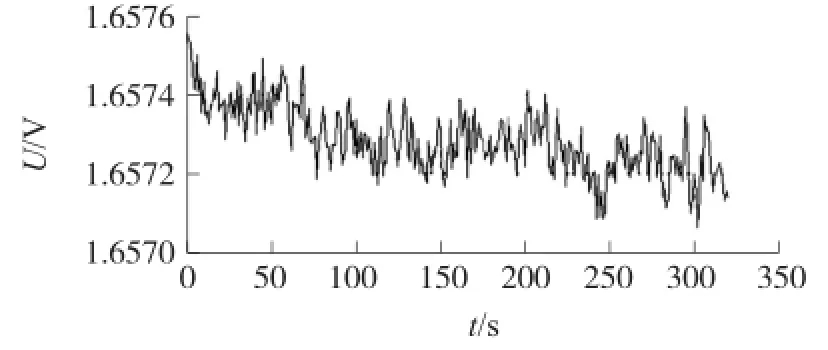
图1　陀螺仪零点漂移信号

2.2补偿方法的选取

从理论上看，MEMS陀螺仪零点漂移是随机的，然而，对大量同一型号的陀螺仪零漂信号采集的过程中发现，零漂的趋势并不是毫无规律可循。受未知的外部环境和内部因素影响，零漂信号中常含有一定趋势项［8］，同一型号陀螺仪的漂移曲线存在相似性，可以通过对零漂曲线的拟合，归纳出其中隐含的函数关系，推导出拟合曲线的回归方程，对陀螺仪的零点漂移误差进行补偿。类似于陀螺仪的标定，我们在使用陀螺仪前对其零点漂移信号进行采集，归纳该陀螺仪零点漂移的特性［9］，在实际应用中，首先对MEMS陀螺仪输出的零漂信号进行滤波，然后用补偿处理后输出数据进行惯性测量运算，以便得到更高的姿态测量精度［10］。

①最佳拟合直线法：

设拟合直线为：Y=A+BX，yi为实际输出零点电压，yi-Yi为第i个点与拟合直线的偏差。令：

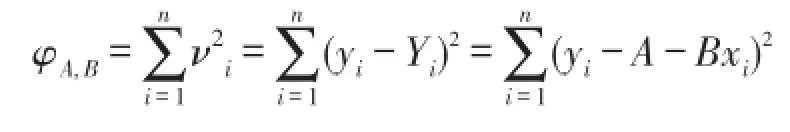
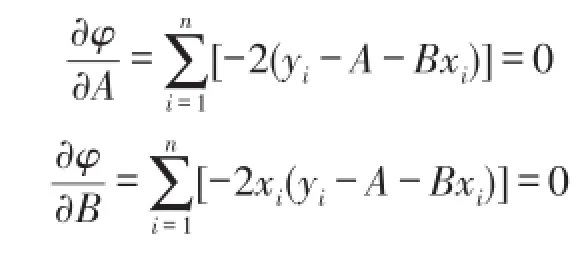
对于两个未知数，方程有唯一解：

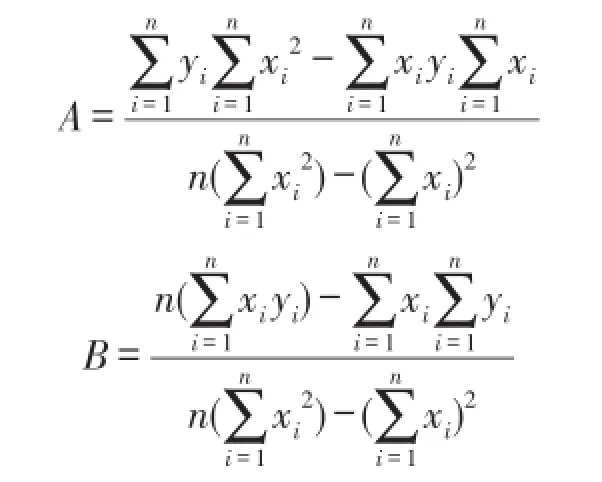
根据上式编写MATLAB程序，计算出截距A和斜率B，即可得到回归方程。

②多项式拟合曲线法：

设拟合直线：Yn（x）=a0+a1x+a2x2+··· 偏差为：

I最小时的Yn（x）即为所求的回归方程；令偏导数等于零：

可得到关于a0，a1···an的线性方程组，从中解出ak（k=0，1，···n），得到对应阶数的回归方程。

2.3补偿效果对比

①最佳拟合直线结果（图2）

U=-7.383×10-6T+1.6509

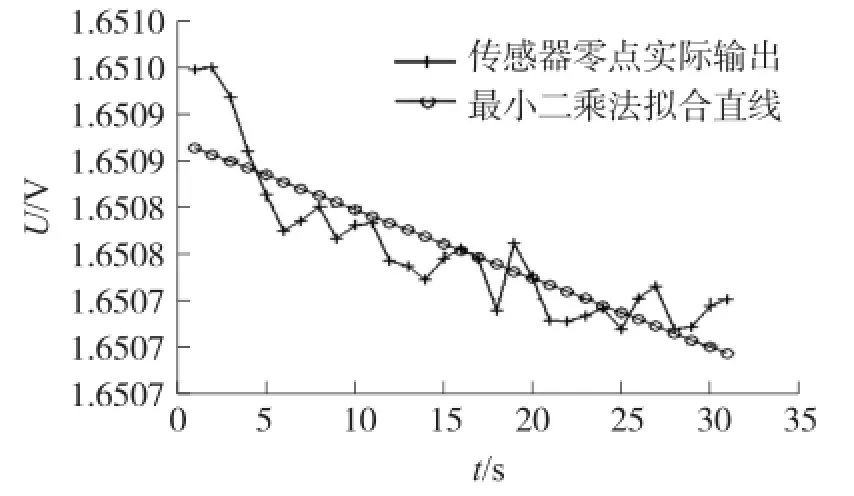
图2　最佳拟合直线

②阶多项式曲线拟合结果（图3）

U=4.0417×10-9T2+（-2.0317×10-6）T+1.6510

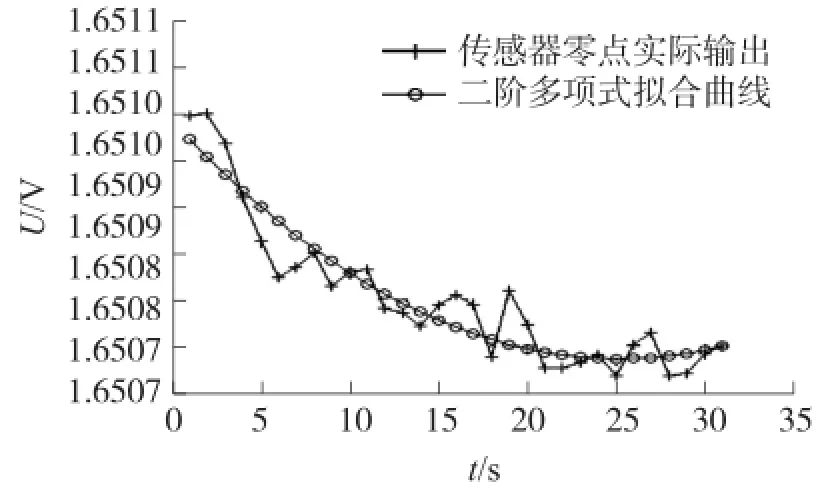
图3　二阶多项式拟合曲线

③阶多项式曲线拟合结果（图4）

U=-1.9117×10-11T3+1.3218×10-8T2+（-3.2249）×10-6T+1.6510

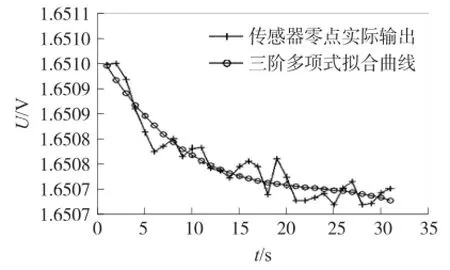
图4　三阶多项式拟合曲线

④阶多项式曲线拟合结果（图5）

U=2.7462×10-13T4+（-1.9487）×10-10T3+ 4.977×10-8T2+（-5.9228）×10-6T+1.6511

图5　四阶多项式拟合曲线

从表1可以看出，当数据点较多时，多项式拟合阶数设置过低，会导致拟合效果不理想［12］。在一定范围内，提高拟合曲线的阶数可以改善拟合效果，但阶数设置过高又带来计算上的复杂性及存储空间的占用［13］。综合考虑以上两方面因素，本文选取4阶多项式曲线拟合。以单轴MEMS陀螺仪为例，由于陀螺仪零点漂移引入误差，未补偿时在300 s内累积角度误差大于6°，采用补偿算法后，累积的角度误差得到有效修正，且误差波动小，不随时间发散。补偿前后角度误差对比如图6所示。

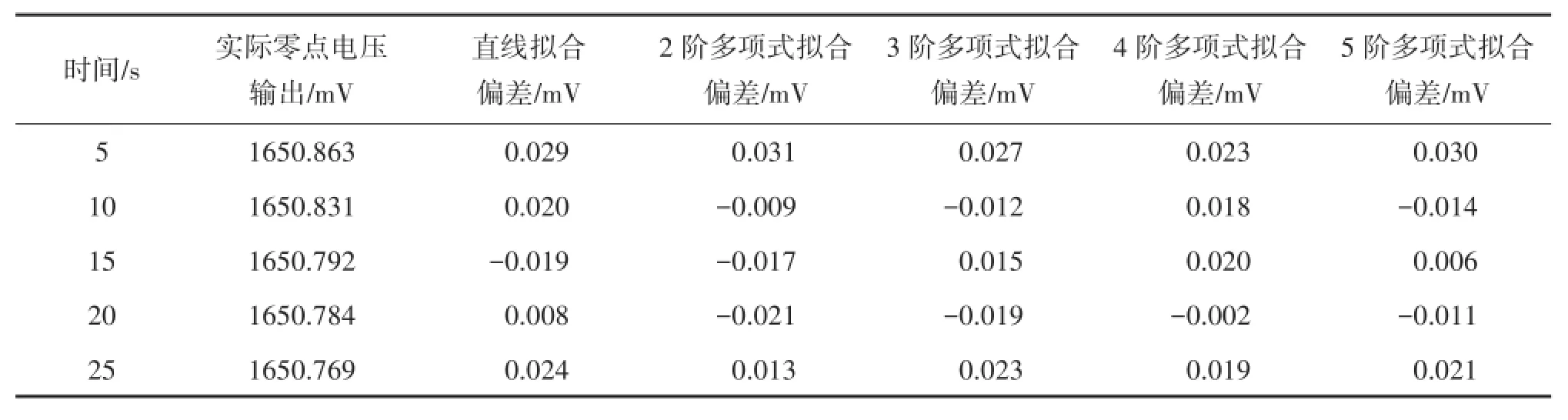
表1　拟合偏差比较

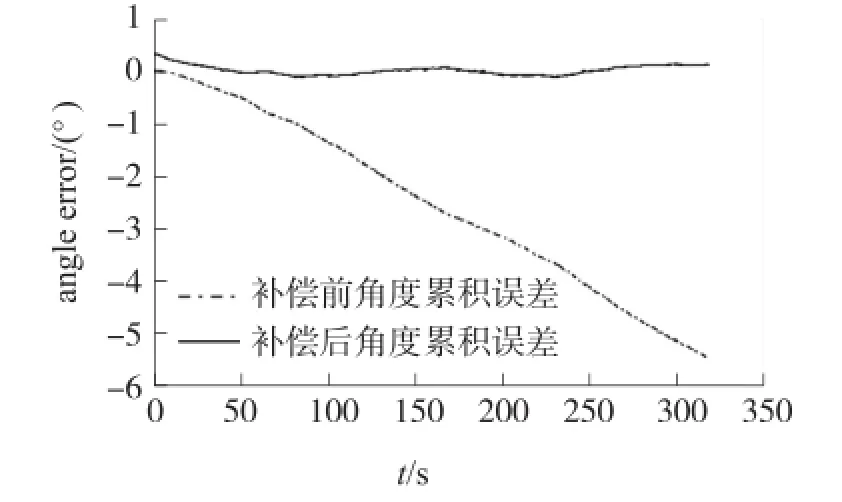
图6　角度累积误差补偿前后对比

3　试验验证

为了验证MEMS陀螺仪零点漂移补偿方法在实际跑车环境下的效果以及加入补偿后导航系统的姿态测量精度，笔者设计了以下跑车试验：选取两套相同的微机电惯导系统，一套灌入添加陀螺仪零点漂移补偿的解算程序，另一套采用不做零点补偿的普通解算程序作为参照，两套系统置于同一测试平台上。每次试验均按照初始对准300 s，跑车100 s的流程进行，跑车路段可近似为直线。试验全程均有高精度GPS信号接收，为后面姿态精度验证提供基准。以高精度GPS数据为参考标准，车载试验三轴姿态角补偿前后对比如图7所示，可以看出，加入补偿后系统的姿态解算结果更接近于GPS的实际输出。

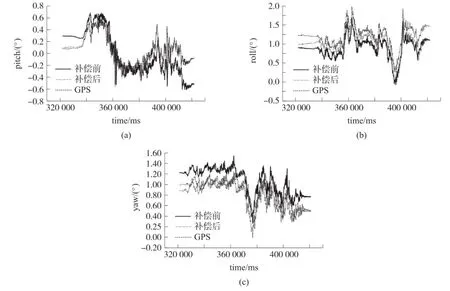
图7　车载试验三轴姿态角补偿前后对比

4　结束语

本文探讨了MEMS陀螺仪零点随机漂移补偿方法，提出了基于最小二乘法的最佳直线及多项式的拟合方案，并对不同阶数的多项式曲线拟合结果进行对比分析，选取效果最佳的补偿方案应用于惯性导航系统的姿态算法中，通过实地跑车试验证明了该补偿方法的有效性，为实际应用中减小MEMS陀螺仪零点漂移随机误差提供了一种思路。

［1］李杰，马幸，刘俊，等.小型惯导系统数据实时采集处理与存储设计［J］.中国惯性技术学报，2008，16（3）：274-277.

［2］李杰，刘俊，张文栋.微惯性测量装置［J］.仪器仪表学报，2006，27（6）：1450-145l，1462.

［3］宋鹏飞，王厚军，曾浩.高速深存储数据采集系统研究与设计.［J］仪器仪表学报，2012；33（01）：42-48

［4］李杰.基于时间序列分析的Kalman滤波方法在M EMS陀螺仪随机漂移误差补偿中的应用研究［J］.传感技术学报，2006， 19（5）：2215-2219.

［5］李杨，胡柏青，覃方君，等.MEMS陀螺的抗野值自适应滤波降噪方法［J］.压电与声光，2015，37（4）：590-594.

［6］徐定杰，苗志勇，沈锋，等.MEMS陀螺随机漂移误差系数的动态提取［J］.宇航学报，2015，36（2）：217-223.

［7］王励扬，翟昆朋，何文涛，等.低成本MEMS陀螺实时滤波方法［J］.电子技术应用，2015，41（1）：50-52，56.

［8］袁赣南，梁海波，何昆鹏，等.MEMS陀螺随机漂移的状态空间模型分析及应用［J］.传感技术学报，2011，24（6）：853-858.

［9］王展飞，鲁文高，李峰，等.MEMS振动陀螺闭环自激驱动的理论分析及数值仿真［J］.传感技术学报，2008，21（8）：1337-1342.

［10］吴峰，王向军，汤其剑，等.基于数字调节方法的MEMS陀螺零位补偿技术研究［J］.传感技术学报，2012，25（12）：1717-1721.

［11］Kevin King，Yoon S W，Perkins N，et al.Wireless MEMS Inertial Sensor System for Golf Swing Dynamics［J］.Sensors and Actua⁃tors，2008，（141）：619-630.

［12］吉训生，王寿荣.小波变换在MEMS陀螺仪去噪声中的应用［J］.传感技术学报，2006，19（1）：150-152.

［13］刘俊，石云波，李杰，微惯性技术［M］.北京，电子工业出版社，2005.

杜瑾（1991-），女，汉族，中北大学硕士研究生，主要研究方向为MEMS器件与组合导航技术等，454552639@qq.com；

李杰（1976-），男，教授，博士生导师，主要研究方向为微系统集成理论与技术，惯性感知与控制技术，组合导航理论，计算几何与智能信息处理等，lijie@nuc.edu.cn。

Zero Drift Random Error Compensating Methods for MEMS Gyros Based on Polynomial Fitting Algorithnm*

DU Jin1，LI Jie1，2*，FENG Kaiqiang1，LIU Yiming1
（1.North University of China Science and Technology on Electronic Test&Measurement Laboratory，Taiyuan 030051，China；2.Key Laboratory of Instrumentation Science&Dynamic Measurement（North University of China），Ministry of Education，Taiyuan 030051，China）

The undesirable accuracy of MEMS sensor limits the range of its application.The compensating method for MEMS gyroscope random drift error is discussed.According to actual test data of gyroscope，the equation of fit⁃ting curve was deduced and compensating effect of different kinds of fitting methods were compared.The car experi⁃ments were carried out to prove that this compensating method can restrain drift random error of gyros and improve navigation accuracy effectively.

MEMS gyroscope；error compensate；least square method；zero drift

TP212.9

A

1004-1699（2016）05-0729-04

项目来源：国家自然科学基金项目（51575500）

2015-12-12修改日期：2016-01-19