基于正则化回归的组学数据变量筛选方法*

哈尔滨医科大学卫生统计学教研室(150081)

谢宏宇　侯　艳　李　康△



基于正则化回归的组学数据变量筛选方法*

哈尔滨医科大学卫生统计学教研室(150081)

谢宏宇侯艳李康△

近年来，随着各种生物检测技术的发展，医学研究中出现了各种高通量数据，如基因组、蛋白质组和代谢组学数据等，变量选择是生物标志物识别和建立分类模型的重要环节，由于高维组学数据中的绝大多数变量对分类并不起作用，并且存在多重共线性、模型过拟合等问题，传统的基于最小二乘方法估计的线性回归并不适用于高维数据[1]。在高维组学数据特征变量筛选过程中，由于变量数目很多，子集筛选方法计算量巨大，并可能由于选择不同的筛选准则导致筛选的结果有很大差异[2]；维数缩减方法虽然能够避免计算量大的问题，但是由于模型中的变量不再是原始变量，模型的可解释性差；而正则化回归方法由于在解回归方程的过程中可以同时实现参数估计和变量筛选，且计算速度快，对变量数目没有限制，因此受到研究者的关注[3]。这类方法不仅能够用于单一组学数据的变量筛选，同时也能拓展到多组学数据融合的情况，因此在实际中具有很好的应用前景。本文将对正则化回归方法及在高维组学数据中的应用做一综述。

正则化的基本原理

正则化是指在原有的损失函数的基础上增加惩罚回归系数的正则项。记β=(β1,β2,…,βm)为回归系数，m为总自变量的个数，则在线性回归中，通过最小化损失函数可以得出对应模型的回归系数估计值

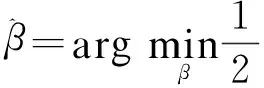
(1)

其中‖·‖2是L2范数，表示向量各元素平方和的平方根，该式表示取右端函数最小值的模型参数，这实际是传统的最小二乘估计。当变量个数较多时，利用该式估计得出的回归模型存在过拟合的风险，正则化则可以在保留所有特征变量的情况下，避免过拟合的发生，其基本原理是通过增加的正则项，减少所有特征变量回归系数估计值的数量级，具体的表现形式如下：

(2)

其中，λP(β)表示正则化项，λ为正则化参数，P(β)为回归系数的惩罚函数，主要目的是用来平衡模型对样本数据的拟合程度以及回归模型的预测能力。在正则化项中，如果正则化参数设定较大会使得每个回归系数估计值偏小；如果回归系数估计值小到一定程度时，相当于因变量只等于常数项，类似于拟合了一条水平直线，导致欠拟合，产生过高的偏差。如果模型中涉及到高阶项，则回归系数的估计值越小，对应的曲线越光滑，从而使函数得到简化，实际中需要选择合适的正则化参数值。目前正则化参数的选择可以通过偏差原理、Engl误差极小原理、Hansen 的L曲线准则、拟最优准则和交叉验证等方法进行确定[4]。回归模型的系数估计值可以通过梯度下降等方法进行求解。

基于正则化回归的单一组学数据变量筛选方法

1.岭回归

岭回归(ridge regression)方法由Hoerl 和Kennard提出[5]，其基本思想是在传统最小化残差平方和基础上加入回归系数的L2范数惩罚项从而收缩回归系数。最小化回归系数的L2范数，会使稀疏矩阵中每个元素的值都很小，但并不一定为0。回归系数估计值的表达式如下：

(3)

其中λ是正则化参数。由于L2范数可以收缩回归系数估计值，因此能够在一定程度上避免模型的过拟合。岭回归的主要特点是通过L2范数对回归系数的连续收缩，能够使每个变量的系数变小，从而通过损失无偏性提高了模型的预测能力。主要缺点是，岭回归将所有的预测变量均保留在模型中，因此在分析高维组学数据时会导致模型的可解释性较差。

2.lasso回归

Tibshirani于1996年提出了基于线性回归的最小化的绝对收缩和选择算子(least absolute shrinkage and selection operator,lasso)来收缩回归系数，这种方法在损失函数中增加了回归系数的L1范数惩罚项，表示为‖·‖1，代表向量中各个元素绝对值之和。在回归系数的绝对值之和小于一个常数的约束条件下，使残差平方和最小化，能够使部分回归系数等于0，同时实现回归系数收缩和变量筛选，从而提高了模型的可解释性[6]。回归系数估计值的表达式如下：

(4)

随着正则化参数λ的增大，lasso方法能够不断地缩小回归系数的估计值，使其趋近于0，实现回归系数的稀疏化。在高维组学数据中，最常用于估计lasso回归系数的方法为最小角算法(least angle regression，LARS)[7]，这种算法相对于最小二乘回归能够很好地解决lasso回归的计算问题。lasso回归存在一定的局限性，即在自变量个数m远大于样本量n时，只能保证lasso回归中最多选择n个变量；同时，如果一组变量高度相关时，这种算法只倾向于选择其中之一，而不关心选择的究竟是哪个变量[5]。

3.自适应lasso回归

Zou(2006)发现lasso回归中L1范数惩罚项对所有回归系数惩罚强度相同，从而导致了回归系数估计值不具有渐进正态性[8]。另外，lasso回归只有在两种特定条件下的变量筛选才具有相合性[5]。为了解决这个问题，Zou(2006)提出了一种新的lasso回归方法，即自适应lasso回归，回归系数估计值的表达式为

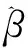
(5)

其中wj代表回归系数的权重。该方法的特点是可以对不同的系数设置不同的惩罚权重，从而改进其估计值的准确性。如果依赖于数据本身对权重做出恰当的选择，则自适应lasso回归具有相合性和渐进正态性，并且能够避免局部最优化的问题[9]。Breheny在2013年将自适应lasso回归方法用于微阵列数据进行变量筛选[10]，并采用预测误差均方作为评价指标与lasso回归进行比较，结果表明自适应lasso回归方法的预测误差均方小于lasso回归，并且筛选出的差异变量更少[11]。

4.朴素弹性网和弹性网算法

高维组学数据往往具有高度相关性和分组特征(例如来自于同一通路的基因)，如前所述lasso回归方法针对以上两种情况进行变量筛选效果不理想。因此Zou于2003年提出了弹性网算法(elastic net)[12]，该方法既能够同时实现变量的自动筛选和回归系数的连续收缩，又能够保证选择出同一分组内与因变量相关性大的变量。朴素弹性网(naive elastic net)算法是最基础的弹性网算法，主要是将lasso回归的惩罚项和岭惩罚项相结合，其表达式为

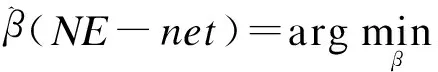
(6)

其中，λ1和λ2均为非负的正则化参数。若记α=λ2/(λ1+λ2)，上式等价于

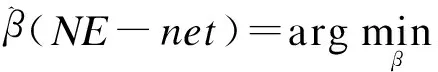
(7)

并且(1-α)‖β‖1+α‖β‖2≤t

其中，t为一个常数界值，(1-α)‖β‖1+α‖β‖2称为弹性网惩罚，α∈[0,1]。当α=0时，该式为lasso回归惩罚项；当α=1时，为岭回归惩罚项。

朴素弹性网算法的参数估计分为两个阶段：首先固定λ2找到岭回归系数，然后通过λ1进行系数压缩。虽然朴素弹性网算法能够克服传统lasso回归的部分不足，但模拟实验表明只有当它接近岭回归或者lasso回归时，才能获得较理想的变量筛选结果。因此，Zou于2005年又提出了对朴素弹性网系数进行重缩放，这种方法即为目前的弹性网算法。当对预测变量进行标准化后，弹性网方法的回归系数与朴素弹性网的回归系数之间具有如下关系：

(8)

其中1+λ2为收缩因子。

研究结果表明，弹性网算法与lasso回归和岭回归相比具有较好的筛选变量的性能，L1范数可以实现自动变量筛选，L2范数可以实现连续收缩，尤其在自变量之间存在较强的相关性时，弹性网算法能够明显的提高预测的准确性[3]。Zou将几种变量筛选方法应用于白血病患者的基因表达数据，目的是筛选用于诊断和预测白血病分型的基因。结果表明，弹性网算法构建的模型分类效果优于支持向量机和惩罚logistic回归等方法，并且能对组内基因进行筛选。由于弹性网算法估计出的系数不具有相合性和渐进正态性[5,8]，因此Zou于2009年提出将自适应加权L1惩罚纳入到弹性网算法正则项中提高估计准确性，即自适应弹性网算法(adaptive elastic-net)，该方法可以将其视为弹性网算法和自适应lasso的结合，具有相合性和渐进正态性[13]。

正则化参数λ决定了模型中回归系数估计值的大小和稀疏化的程度。确定正则化参数的基本方法有交叉验证[14]、贝叶斯信息准则(BIC)[15]、Cp统计量[7]和赤池信息量准则(AIC)[16]。Zou于2007年从变量筛选的角度证明了BIC相对于其他方法更适用于参数值的选择，该方法能够产生一个更加稀疏的模型[12]。Chen等认为使用BIC准则在高维数据中筛选变量的标准具有一定的任意性，因此提出了扩展的BIC方法(EBIC)，这种方法既考虑了未知参数的个数，也考虑了模型空间的复杂性，并且能够更加严格地控制差异变量错误发现率[17]。

5.分组lasso回归

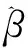
(9)

其中L为变量的组别数，l=1,2,…,L，X(l)代表组l中与因变量有关的X列的子矩阵，β(l)是组的系数向量，pl是第l组中包含的变量个数。这种方法利用了‖β(l)‖2在β(l)=0处不可微的性质，将该组从模型中剔除。其主要思想是筛选出对因变量有影响的特征组，同时通过选择合适的参数λ调整组别个数，λ值越大，对各分组作用的惩罚越大，则模型中保留的组数越少。虽然分组lasso回归能够实现对组别的筛选，但是只能筛选出模型中整个组内的变量回归系数β(l)=0的特征组，这一缺点限制了其应用。当每个特征组内只包含一个自变量时，则该方法即为传统的lasso方法。

6.稀疏组lasso回归

实际研究中不仅仅需要实现组别的稀疏化，同时还需要实现组内变量的稀疏化，例如，研究者识别感兴趣基因通路，同时对该条基因通路中的关键基因进行筛选。因此Simon(2010)提出将lasso回归和分组lasso回归相结合，引进了稀疏组lasso(sparse-group lasso)回归[19]，其表达式为

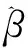
(10)

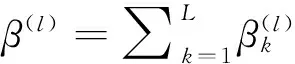
稀疏组lasso回归的方法与弹性网方法相似，不同点在于该种方法是利用在惩罚回归系数为0时不可微的性质，将稀疏为0的组别从模型中去除，实现组间稀疏化，而弹性网方法则保留了所有的分组。Simon(2013)将lasso回归、分组lasso回归和稀疏组lasso回归的方法应用于乳腺癌患者的基因表达数据中，并比较了三种方法的筛选效果。结果表明稀疏组lasso回归的变量筛选性能优于lasso回归和分组lasso回归：稀疏组lasso回归的分类正确率达到70%，而分组lasso回归和lasso回归的分类正确率分别为60%和53%。由于在癌症数据中添加分组的信息对于分类非常有意义，同时分组信息可以帮助更加深入的了解生物学机制，因此对于癌症数据的分析，稀疏组lasso回归的方法有很大的优势[19]。

多组学融合数据变量筛选方法

传统的变量筛选方法一般均可应用于单一组学数据的变量筛选，如基于回归、基于机器学习和基于网络的方法等，目前应用于多组学融合数据变量筛选方法相对较少，而基于正则化的变量筛选方法可以实现多组学数据的融合和变量筛选。

1.稀疏广义典型相关分析

典型相关分析(canonical correlation analysis，CCA)是用于研究两组变量之间关系的常用方法。Tenenhaus于2011年提出了正则化的广义典型相关分析(regularized generalized canoncial analysis，RGCCA)方法，该方法可用于分析三个或者更多的变量集合间的关系[20]。RGCCA是一种基于主成分分析的方法，用于研究多个数据集中变量之间的关系。RGCCA成分的性质和解释性受每组变量之间有用性和相关性的影响。RGCCA主要基于使多个数据样本中生成新的综合变量的相关程度最大化的思想进行求解。

实际中，在每组变量中识别出在组间关系中起显著作用的变量子集非常重要，因此Tenenhaus在2014年提出了稀疏的广义典型相关分析(sparse generalized canonical correlation analysis，SGCCA)，这种方法通过对外部权重向量加上L1惩罚，在同一方法中结合了RGCCA和L1惩罚项[20]。Tenenhaus将SGCCA方法应用到儿科神经胶质瘤数据，结果表明：与RGCCA比较，SGCCA方法能够筛选出在组间相关作用中具有更小差异的变量组合[21]。

2.稀疏偏最小二乘回归

偏最小二乘(PLS)的变量筛选方法已经成功地应用于代谢组学数据。其主要原理是分别在自变量和因变量中提取出成分，使各自提取出的成分尽可能多的解释各数据的变异信息，同时使提取成分的相关程度达到最大。

Cao(2008)在此基础上提出了稀疏偏最小二乘回归(sparse least squares regression,SPLS)的变量筛选方法，该方法能够同时实现数据的整合和变量筛选，其主要思想是在PLS的基础上，通过Q2值作为评价指标对构建模型的成分数量进行选择，同时对每个成分加上lasso惩罚，实现变量筛选。研究表明：该方法应用于高维数据集分析时，与PLS相比具有更高的稳定性，能够更好地进行变量筛选[22]。

3.结构组稀疏算法

多尺度数据分析的关键性问题是，数据结构异质性整合和特征变量筛选的稳定性。基于结构组稀疏算法(structure grouping sparsity，SGS)的多尺度数据变量筛选方法的目的是根据实际数据给出一个可以解释和预测的模型。其主要思想是，根据实际数据建立应变量Y与自变量X=(X1,X2,…,Xm)关系的广义线性模型(可拓展至非线性)，实现对不同来源的异质性数据在不同水平上进行组间和组内特征筛选。其表达式为：

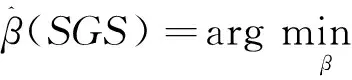
(11)

展　　望

基于正则化回归的变量筛选方法，克服了传统变量筛选方法的不足，且随着研究的深入，需要不断的更新和发展。该方法的发展一直围绕着拟合较好的模型应该具有预测准确度高、模型的可解释性强的特点；本着模型本身具有优良的参数估计性质，即无偏性、有效性、相合性和渐进正态性。基于正则化的变量筛选方法不仅能够应用于单一组学数据的变量筛选，也能够应用于多组学数据的融合和变量筛选。然而，这种方法的惩罚项选择及其统计性质，以及参数求解等问题都有待进一步研究。展望未来，高维组学的数据研究将实现跨组学的超高维变量筛选，从而更全面的研究疾病的发生机制，因此这类方法将会具有较好的前景。

[1]赵奕林，朱真峰，周清雷.适用于大规模高维多类别数据分类的并行非线性最小二乘分类器.小型微型计算机系统，2014,3:579-583.

[2]Daniel PB,Pierluigi C.Introduction to the theory of complexity.Prentice Hall.ISBN 0-13-915380-2,1994.

[3]Zou H,Hastie T.Regularization and variable selection via the elastic net.J.R.Statist.Soc.B,2005,67:301-320.

[4]闵涛，葛宁国，黄娟，等.正则参数求解的微分进化算法.应用数学与计算数学学报,2010,24(2):23-27.

[5]Hoerl A,Kennar R.Ridge regression.In Encyclopedia of Statistical Sciences,1998,8:129-136.

[6]Tibshirani R.Regression shrinkage and selection via the lasso.J.R.Statist.Soc.B,1996,58:267-288.

[7]Efron B,Hastie T,Johnstone I,et al.Least angle regression.Ann.Statist.,2004,32:407-499.

[8]Zou H.The adaptive lasso and its oracle properties.Journal of the American Statistical Association,2006,101:1418-1429.

[9]Li ZT,Mikko J,Sillanpaa.Overview of lasso-related penalized regression methods for quantitative trait mapping and genomic selection.Theor Appl Genet,2012,125:419-435.

[10]Scheetz T,Kim K,et al.Regulation of gene expression in the mammalian eye and its revevance to eye disease.Proc.Natl.Acad.Sci,2006,103:14429-14434.

[11]Patrick B,Jian H.Group descent algorithms for nonconvex penalized linear and logistic regression models with grouped predictors.Stat Comput,2015,25:173-187.

[12]Zou H,Hastie T.Regression shrinkage and selection via the elastic net,with application to microarrays,2003，1-26.

[13]Zou H,Zhang H.On the adaptive elastic-net with a diverging number of parameters.Ann.Statist.,2009,37:1733-1751.

[14]Hastie,Tibshirani R,Friedman JH.The elements of statistical learning.Springer,New York,2009.

[15]Zou H,Hastie T,Tibshirani R.On the “degrees of freedom” of the lasso.Ann Stat,2007,35:2173-2192.

[16]Akaike H.New look at the statistical model identification.IEEE T Autom Contr,1974,19:716-723.

[17]Chen J,Chen Z.Extended Bayesian information criteria for model selection with large model spaces.Biometrika,2008,95:759-771.

[18]Yuan M,Lin Y.Model selection and estimation in regression with grouped variables.Journal of the Royal Statistical Society,Series B,2007,68(1):49-67.

[19]Simon N,Friedman J,et al.A Sparse-Group lasso.Journal of computational and Graphical Statistics,2013,22:231-245.

[20]Tenenhaus A,Tenenhuas M.Regularized generalized canonical analysis.Psychometrika,2011,76:257-284.

[21]Tenenhaus.Variable selection for generalized canonical correlation analysis.Biostatistics,2014:1-15.

[22]Le Cao KA,Rossouw D,et al.A sparse PLS for variable selection when integrating omics data.Stat Appl Genet Mol Biol,2008,7(1)：1-32.

(责任编辑：郭海强)

国家自然科学基金资助(81573256，81473072)；黑龙江省博士后资助经费(LBH-Z14174)

李康,E-mail:likang@ems.hrbmu.edu.cn