Laplace变化在有源滤波器电路仿真中的应用与研究
2016-10-26刘德全
刘德全
(宁夏师范学院,固原756000)
Laplace变化在有源滤波器电路仿真中的应用与研究
刘德全
(宁夏师范学院,固原756000)
拉氏变换(Laplace)是控制工程应用中的一种基本的数学方法,时间函数的导数或者微分运算经过Laplace变换后转换为复变量s域的代数运算。据此,在电路分析中,元器件的伏安特性关系可以在复频域中进行表示,即电阻元器件
Laplace;电路仿真;s域;运算放大器
0 引言
Laplace变换在《电路》、《自动控制原理》、《信号与系统》等课程[1-8]以及实验中应用非常广泛,但其应用思路先给出电路图,按照电路模型将时域中的电路利用相关的复频域电路模型代替,利用一定的定理进行求解分析。王瑜[9]浅谈了积分变换在电路分析中的应用,积分变换中的傅里叶变化和拉普拉斯变换在电路中应用非常广泛,对于直流电路中,在时域分析电路比较简单,但是如果在正弦稳态电路中,利用复阻抗求解电路非常的难,利用向量法求解应用而生,在复频域进行求解。对于非正弦信号可由傅里叶变换转换成直流分量和有限项的正弦信号,这样就可以用相量法进行求解,但相量法求解也很麻烦,这时就将jω=s代替,形成拉普拉斯变换。拉普拉斯变换比相量法求解更简单。蒋鹏、陈元莉[10]研究了拉普拉斯变换在线性动态电路分析的应用,拉普拉斯解线性动态电路优点很多,除了将时间函数的导数或者微分运算经过Laplace变换后转换为复变量s域的复频域响应,另外Laplace变换式中换包含了动态元器件的初始条件值,这样使动态电路的系统的全解一步求解,因此Laplace变化是分析复杂线性动态电路的有效工具。侯新杰、许海波等[11]人对特殊电路的暂稳态响应应用拉普拉斯方法进行了求解。袁艳红[12]对RLC电路应用拉普拉斯进行了分析,对分析的结构进行逆拉普拉斯变换就得到了时域的解。罗飞[13]、牛皖闽[14]、宋玉玲[15]对卷积积分和拉普拉斯变化在一阶电路中的解法进行了对比,得到的结果是在高阶动态电路中用拉普拉斯分析更简单。
上述可以看出,拉普拉斯在电路中的分析应用很广泛,是很重要的内容,但上面的论述都存在一个共性问题,都是对电阻、电容和电感组成的电路进行分析,在应用拉普拉斯方法分析电路。但在实际应用中确是反向的,一般是对实际中的问题进行建模,对含有运算放大器的组成的电路进行Laplace变换分析甚少,本文以有源低通滤波器的设计为例说明此问题的具体的分析方法。
1 有源低通滤波器电路的Laplace变化
有源低通滤波器的电路如图1所示。对图1中的元器件用拉普拉斯模型替代,即电阻R的模型仍为R,电容C的模型为
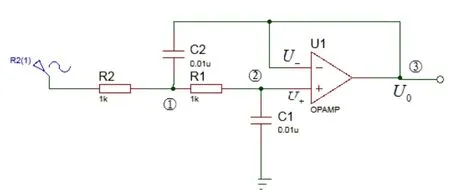
图1 有源低通滤波器电路

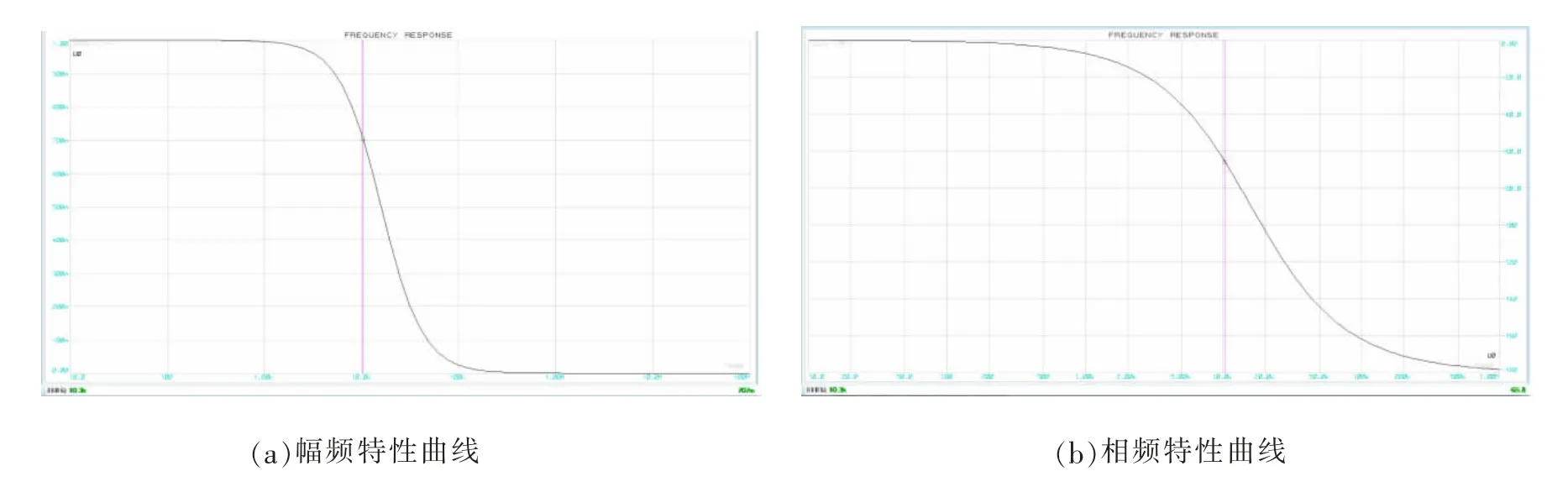
图2 频率特性曲线

2 低通滤波器的特性测试仿真
在Proteus 8.4中绘制图1所示电路图,设输入信息号Ui=1V,频率f=100Hz的正弦信号,在原图中添加Frequency图表,该图表可以描述电路的幅频特性和相频特性。在研究幅频特性曲线时,一般使输入信号的幅度固定,研究输出信号的幅度(或者电压放大倍数)随频率变化而变化的特性曲线,放大电路对不同频率分量的信号放大能力是不相同的,而且不同频率的信号通过放大电路后还会产生不同的相移。因此,衡量放大电路放大能力的放大倍数也就称为频率的函数;在研究相频特性曲线时,是研究输出信号与输入信号之间的相位差随频率变化而变化的曲线[16]。仿真得到幅频特性曲线,如图2(a)所示,从图中的测试数据得到当fH=10.3K时AH=0.707,在误差的允许范围内,理论与仿真是一致的。图2(b)是相频特性曲线,从图2(b)中可以看出,此时相频特性将滞后65.8°。
3 结语
本文对含有运算放大器的电路进行了拉普拉斯变换分析,简化了分析方法,最后在Proteus软件上进行了波特图仿真分析,仿真分析与理论分析相吻合,验证了拉普拉斯变换在运算放大器构成的电路中进行变换的正确性。
[1]邱关源,罗先觉.电路,高等教育出版社[M].北京:高等教育出版社.
[2]Charles K.Alexander,Matthew N.O.Sadiku著;段哲民,周巍,李宏等译.电路基础(第五版)[M].北京:机械工业出版社.
[3]James W.Nilsson(詹姆斯W.尼尔森),Susan Riedel(苏珊A.里德尔)著.电路(第10版).周玉坤,李莉等译.北京:中国工信出版集团.
[4]尼尔森(James W.Nilsson),(美)里德尔(Susan.Riedel)著.电路(第9版)(英文版).Electric Circuits Ninth[M].北京:电子工业出版社.
[5]吴大正.信号与线性系统分析[M].北京:高等教育出版社.
[6]郑君里.信号与系统[M].北京:清华大学出版社.
[7]胡寿松.自动控制原理[M].北京:科学出版社.
[8]Gene F.Franklin(吉尼F.富兰克林),J.David Powell,Abbas Emami-Naeini等著.李中华等译.自动控制原理与设计(第六版)[M].北京:电子工业出版社.
[9]王瑜.浅谈了积分变换在电路分析中的应用[J].山西师范大学学报,2010(24):20-21.
[10]蒋鹏,陈元莉.拉普拉斯变换在线性动态电路分析的应用[J].电子技术,2013(10):23.
[11]侯新杰,许海波.用拉普拉斯变换求特殊电路的暂态响应[J].河南技师院学报,1996,24(3):25-28.
[12]袁艳红.应用拉普拉斯变化换分析RLC电路[J].新疆教育学院学报,2001,17(2):93-94.
[13]罗飞.卷积积分和拉普拉斯变换在一阶电路中的应用[J].株洲工业学报,1998,12(1):39-42.
[14]牛皖闽,佟亮,李诚等.关于应用拉普拉斯变换分析复杂性动态线性电路的探讨[J].绥化学院学报,2006,26(6):173-174.
[15]宋玉玲,鲁道邦等.拉普拉斯变换在互感电路分析中的应用[J].南阳师范学院学报,2008,7(6):29-32.
[16]刘德全.Proteus 8—电子线路设计与仿真[M].北京:清华大学出版社,2014,10.
Application and Research on Active Power Filter Circuit Based on Laplace Transform
LIU De-quan
(Ningxia Normal University,Guyuan 75600)
Laplace transform is one of the basic mathematical methods in control engineering applications.Time function of the derivative or differential operation after Laplace transform into algebraic operation of complex variable s domain.Accordingly,in the circuit analysis,the relationship between the voltage and current characteristics of the components can be expressed in the complex frequency domain, the analysis of the Laplace transform which is composed by the complex operational amplifier,puts forward the analysis method of the operational amplifier based on the Laplace transform.
Laplace;Circuit Simulations;Domain;Operational Amplifiers

1007-1423(2016)23-0032-03DOI:10.3969/j.issn.1007-1423.2016.23.008
7-),男,甘肃白银人,讲师,硕士,研究方向为信号与信息处理
2016-06-21
2016-08-10
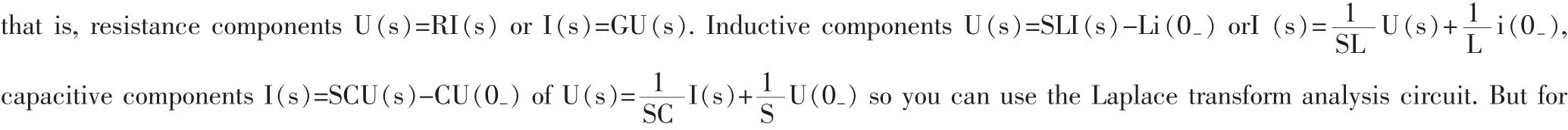
路求解的Laplace变换的分析还比较,提出基于Laplace变换的运算放大器分析方法。
宁夏师范学院科研项目(No.NXSF1661)
