基于Lempel-Ziv复杂度的精神分裂症MEG信号分析
2016-10-26陈振宇黄晓霞
陈振宇,黄晓霞
(上海海事大学信息工程学院,上海200135)
基于Lempel-Ziv复杂度的精神分裂症MEG信号分析
陈振宇,黄晓霞
(上海海事大学信息工程学院,上海200135)
将非线性动力学中的Lempel-Ziv复杂度分析方法应用于精神分裂症的脑磁图(MEG)信号的复杂性研究,探究精神分裂症MEG信号的非线性动力学特性。对10例精神分裂症患者和10个健康正常人(正常对照组)的静息态MEG信号进行Lempel-Ziv复杂度分析,并采用两独立样本t检验方法进行统计学分析。研究发现,精神分裂症患者MEG信号的Lempel-Ziv复杂度明显高于正常对照组。这表明精神分裂症患者比健康正常人有更高的大脑活动复杂性。
非线性动力学;Lempel-Ziv复杂度;脑磁图;精神分裂症
0 引言
脑磁图(Magnetoencephalography,MEG)是一种探测大脑生物磁场信号的脑功能图像技术,能无接触、无侵袭、无损伤地对大脑功能活动的变化情况进行检测。MEG信号的采集可以不受颅骨及头部皮层组织的影响,而且具有高精度的时间分辨率(毫米级)和空间分辨率(毫米级)[1],能准确并实时地反映出脑功能活动变化所引起的脑内神经电流的磁场变化情况。因此在众多脑功能图像技术中,MEG是分析和研究精神分裂症(Schizophrenia)较为理想的工具之一。
研究表明,人体大脑是一个具有高维性的复杂动态系统,大脑神经元的活动特性及其电磁信号的表现具有广泛的非线性、非平稳性等非线性动力学特征[2-3]。相对于传统的信号时域分析方法、频域分析方法及时频分析方法,采用非线性动力学分析方法对大脑电磁信号进行分析能更有效地体现大脑内部功能活动状态的变化情况。许多非线性动力学分析方法陆续被提出用于分析和研究大脑电磁信号的复杂性测度,其中Lyapunov指数、相关维数、熵和复杂度等是比较常用的几种非线性动力学特征量[4]。这些非线性动力学特征量能够量化大脑电磁信号的复杂性强弱程度,从而表征脑功能活动的动态特性。
本研究利用非线性动力学理论中的Lempel-Ziv复杂度这种复杂性测度,研究精神分裂症患者与健康正常人的静息态MEG信号的差异,从非线性动力学的角度分析精神分裂症的症状表现。
1 Lempel-Ziv复杂度算法
Lempel-Ziv复杂度是由Lempel和Ziv提出的一种时间序列复杂性测度分析方法[5]。Lempel-Ziv复杂度是通过对时间序列进行符号化处理后计算其符号序列出现新模式的概率来表征时间序列的复杂度。一个序列的Lempel-Ziv复杂度越高说明出现新模式的概率越高,则这个序列的随机性就越强。Lempel-Ziv复杂度具体算法为:
步骤一:对于某一时间序列X={xi|i=1,2,…,n},计算其平均值:
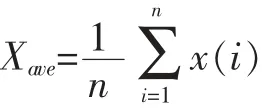
设S=(s1,s2,…,sn)长度为n的空符号串,与时间序列X的长度相同。时间序列中的任一元素x(i),当x(i)>Xave时,取符号si为“1”,否则为“0”。由此建立与原时间序列对应的(0,1)符号序列S。
步骤二:设c(n)为符号序列S=(s1,s2,…,sn)的复杂性计数。令S,Q分别表示两个由(0,1)序列组成的字符串;SQ表示S和Q两个字符串的级联,即SQ=(s1,s2,…,sn,q1,q2,…,qm-1);SQP表示把SQ中最后一个字符删去后所得的字符串,即SQ=(s1,s2,…,sn,q1,q2,…,qm-1)。令V(SQP)表示SQP中的所有不同的子串的集合。
步骤三:将c(n),S和Q分别初始化为c(n)=1,S=(s1),Q=(s2),则SQP=(s1)。
步骤四:若Q∈V(SQP),则表示Q中的字符串是S字符串的一子串,那么把待求的下一个字符级联到Q中,变成S=(s1),Q=(s1,s2)。若Q∉V(SQP),则Q中的字符串不是S字符串的子串,是插入的字符串,这时把Q级联到S,即S=SQ,同时将待求序列的下一个字符添加并替换原来的Q中,此时S=(s1,s2),Q=(s3)。每次Q级联到S时,将c(n)进行c(n)=c(n)+1。
步骤五:重复步骤四,直到待求序列中所有的字符被取完。这样就把符号序列S=(s1,s2,…,sn)分成了c(n)个不同的子串,即可计算得其复杂度。
根据Lempel和Ziv的研究,对于任意足够长的序列,进行二进制符号化后所得的符号序列都会趋向一个定值:
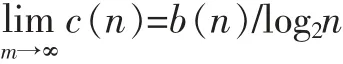
由上式可知,用b(n)来对c(n)进行归一化处理后可得到“归一化复杂度”:
LZC=c(n)/b(n)
LZC值的大小在0至1之间,它反映了时间序列的复杂性程度。LZC值越大说明时间序列的复杂性越高,即越接近随机。反之,若LZC值越小则表示其规律性就越明显。
2 实验数据描述
本研究数据来自美国国立精神卫生研究所MEG科研平台(National Institute of Mental Health MEG Core Facility)。该MEG数据是用加拿大VSM MedTech公司CTF-275超导量子干涉仪(SQUID)的全头型脑磁图设备采集得到的精神分裂症患者及健康正常人在静息态时的MEG信号。每例MEG信号包含有275个通道,采样频率为600Hz,采样时间240秒。实验对象分为患者组和对照组。患者组为10例精神分裂症患者(包括男性和女性,年龄18~30岁);对照组选择10个健康正常人(包括男性和女性,年龄20~35岁),均无神经或精神上的疾病史。
3 数据的统计学分析
应用SPSS统计分析工具对两组样本(患者组和正常对照组)MEG信号的LZC值进行配对t检验,对脑区组间的LZC复杂度进行统计学上的显著性差异分析,并采用多重假设检验中的假阳性错误发现率(False Discovery Rate,FDR)控制方法对结果进行校正,当p<0.05时认为具有显著性差异。
4 实验结果分析
4.1脑区组间差异
实验将全头上的275个通道划分为14个脑区组,即LF、ZF、RF、LC、ZC、RC、LP、ZP、RP、LO、ZO、RO、LT和RT。各脑区组在全头上的划分情况如图1所示:
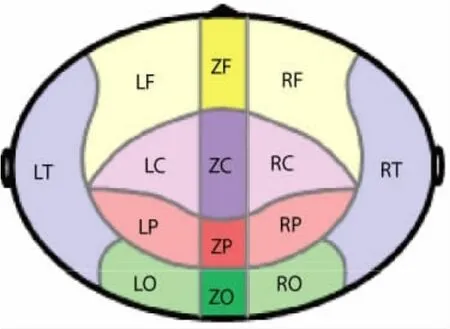
图1 脑区划分图
图2为精神分裂症患者与正常对照组14个脑区的组间MEG信号LZC复杂度均值比较图。从图2中可以看出,患者组中的LZC复杂度均值分布在[0.4045,0.5347],而正常对照组的LZC复杂度均值分布在[0.3766,0.5035]。患者组的LZC复杂度均值全部明显高于正常对照组(p<0.05,FDR校正)。说明精神分裂症患者在静息状态下MEG信号的复杂性高于健康正常人。
图3显示了这14个脑区的组间LZC复杂度的相对差异。其中:

结合图2与图3可以发现,两者最低的相对差异为2.01%,最高相对差异达到10.94%。可见,除了LT脑区上的LZC值非常接近外,其他的脑区上的LZC值均有明显的区分度,能够较好地将它们彼此之间区分开,尤其是LC、LP以及ZP这三个脑区,精神分裂症患者与正常对照组的LZC复杂度相对差异更加明显。
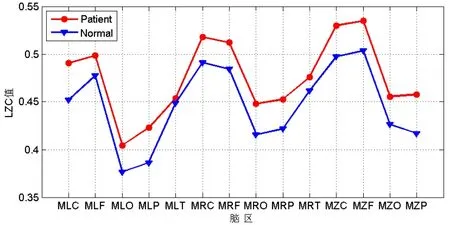
图2 精神分裂症患者与正常对照组LZC值比较图
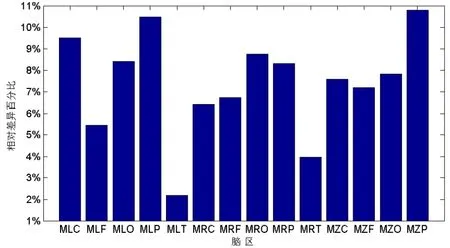
图3 精神分裂症患者与正常对照组LZC值相对差异图
4.2LZC复杂度全头拓扑分布图比较
利用两组样本中所有通道(275个通道)的LZC复杂度均值绘制成全头拓扑分布图(见图4所示)。从图中两者的颜色对比可以看出,精神分裂症患者与正常对照组的LZC复杂度在大部分脑区上的分布表现类似,而额叶所在的脑区(即LF与RF)和中央区(ZC)有较为明显的差异。从整体上看,患者脑区上的深色区域比正常对照组的分布范围更广,可见精神分裂症患者的LZC复杂度比正常对照组的要高,尤其是额叶和中央区的部分更为明显。
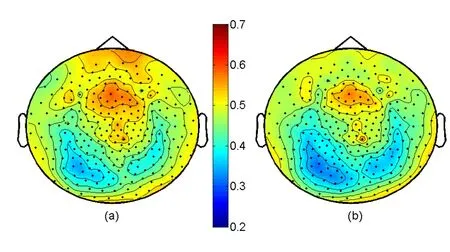
图4 精神分裂症患者(a)与正常对照组(b)的LZC复杂度全头拓扑分布图
5 结语
本文应用非线性动力学中的Lempel-Ziv复杂度分析方法对精神分裂症患者及健康正常人的MEG信号的进行信号的复杂性研究,探究精神分裂症MEG信号的非线性动力学特性。由上述的研究结果可以发现,精神分裂症患者静息态MEG信号的LZC复杂度高于健康正常人,尤其是额叶和中央区的脑区更加明显。这个结论与既往一些精神分裂症EEG研究结果吻合。李颖洁等[6]对62例精神分裂症患者和26名健康正常人的EEG的研究结果也显示了精神分裂症患者的LZC复杂度比正常对照组的高。另外,Takahashi等[7]用多尺度熵(MSE)对22例精神分裂症患者和24名年龄匹配的健康对照者进行分析,也发现精神分裂症患者比健康对照者在额叶-中央区-颞叶这些脑区部位表现出显著高的复杂性。因此,可以得出结论,精神分裂症患者比健康正常人有明显高的大脑活动复杂性。
[1]Vrba J.Magnetoencephalography:the Art of Finding a Needle in a Haystack[J].Physica C Superconductivity,2002,368(1):1-9.
[2]Babloyantz A.Evidence of Chaotic Dynamics of Brain Activity During the Sleep Cycle[J].Physics Letters A,1985,111(3):152-156.
[3]Jeong J,Kim D J,Chae J H,et al.Nonlinear Analysis of the EEG of Schizophrenics with Optimal Embedding Dimension[J].MedicalEngineering & Physics,1998,20(9):669-676.
[4]许敏光,夏鹏,蒋勇,等.应用非线性动力学指标分析大鼠癫痫模型脑电信息变化[J].中国临床康复,2005,9(21):216-218.
[5]Lempel A,Ziv J.On the Complexity of Finite Sequence[J].IEEE Transactions on Information Theory,1976,22(1):75-81.
[6]李颖洁,邱意弘,朱贻盛.脑电信号分析方法及其应用[M].北京:科学出版社,2009.
[7]Takahashi T,Cho R Y,Mizuno T,et al.Antipsychotics Reverse Abnormal EEG Complexity in Drug-Naive Schizophrenia:A Multiscale Entropy Analysis[J].Neuroimage,2010,51(1):173-82.
MEG Signal Analysis of Schizophrenia Based on Lempel-Ziv Complexity
CHEN Zhen-yu,HUANG Xiao-xia
(College of Information Engineering,Shanghai Maritime University,Shanghai 200135)
Applies Lempel-Ziv complexity to analyze the complexity of Schizophrenia Magnetoencephalography(MEG)signals,in order to explore the nonlinear dynamic characteristics of schizophrenia MEG signals,studies 10 patients with schizophrenia and 10 healthy individuals'(normal control group)resting state MEG signal by using Lempel-Ziv complexity analysis method.The result show that Lempel-Ziv complexity of schizophrenia MEG signal is significantly higher than normal control group.It suggests that patients with schizophrenia have higher brain activity complexity than the healthy normal people.
Nonlinear Dynamics;Lempel-Ziv Complexity;Magnetoencephalography;Schizophrenia
1007-1423(2016)23-0003-04DOI:10.3969/j.issn.1007-1423.2016.23.001
陈振宇(1988-),男,广东茂名人,硕士,研究方向为模式识别与信号处理
2016-05-16
2016-08-05
第48批教育部留学回国人员科研启动基金(教外司留(2014)1685号)
黄晓霞(1968-),女,上海人,博士,副教授,研究方向为脑波信息处理与脑机接口
