非线性光束传输方程的tanh-coth解法

徐伟津，卓辉

（湖南农业大学信息科学技术学院，长沙410128）

非线性光束传输方程的tanh-coth解法

徐伟津，卓辉

（湖南农业大学信息科学技术学院，长沙410128）

非线性薛定谔方程的解析解的分析对研究信息的传输有着非常重要的作用，利用tanh-coth法求非线性薛定谔方程得到一系列较好的解析解，对研究光束的非线性传输具有一定的指导意义。

光孤子；非线性薛定谔方程；tanh-coth法

0　引言

自然界的非线性现象是一个普遍问题，而且都可以用非线性薛定谔方程来描述。在非线性光学研究中，也同样可以用非线性薛定谔方程来描述。从上个世纪开始，非线性光学的非线性薛定谔方程已经成为研究的热点，其中对介质中的光束演化的研究也是一个非常重要的问题，其研究成果指导了许多光控制器件的开发。孤子的现象与孤子概念的提出可以追溯到20世纪30年代，起初人们是在水中发现了孤子现象，1973年，光孤子的概念首次提出：光孤子与其他同类光孤子相遇后，其形状，速度，幅度将不会发生变化，随后对其进行了深入研究并推广开来。当前，研究者已经陆续建立了KDV方程［1］，S-G方程，K-G方程［2］及非线性薛定谔方程来描述孤子的相关变化，当前有很多研究者利用逆反射法［3］，Painleve展开法［4］，Hirota双线性法［5］，变分法，数值法等，来解决光学的非线性传输特性问题，得到了非常重要的结论。其中D.Anderson利用变分法求解了光脉冲在光纤中的非线性传输的非线性薛定谔方程得到了啁啾和波包宽度的演化情况［6］，没有给出一个定量的具体的解析解，但非常简洁。本文则着眼于tanh-coth法［7］在非线性薛定谔方程在光孤子通信中的求解，得到了一系列相对较好的解析解。对于光束在非线性介质的传输研究有着重要的研究作用。

1　传输方程与tanh-coth法

1.1传输方程简介

在横向X方向上折射率具有线性周期调制的自聚焦克尔型非线性介质中，光束沿纵向Z方向的传输方程在弱调制近似下满足下面的非线性薛定谔方程：

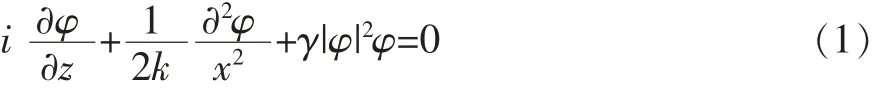
式中，k=n0ω/c=2πn0/ρ，n0是线性折射率，ρ是ρ射光束的波长，γ是介质的。

1.2对于非线性偏微分方程

引入w=x-ct，则将方程（2）化成常微分方程如下：

再引入一个新的独立变量，令：

则有：

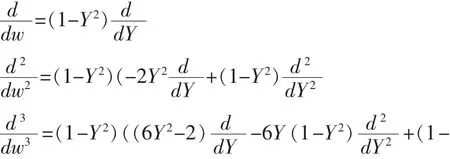
2　简化的传输方程求解

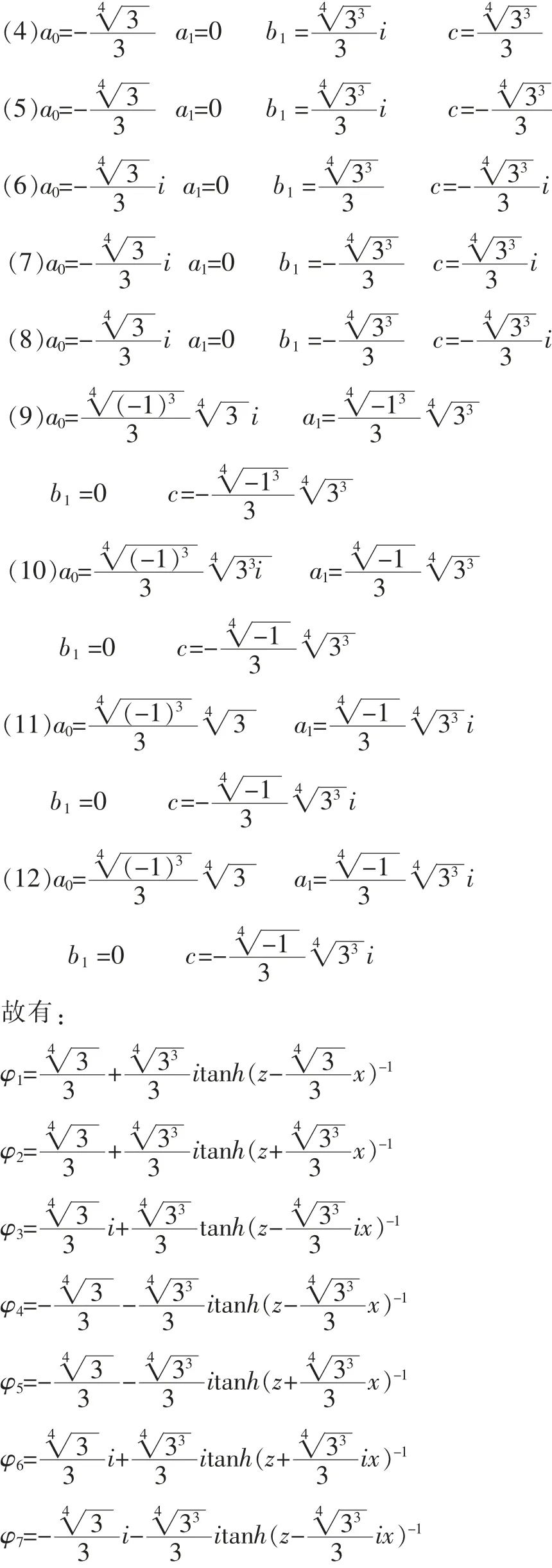
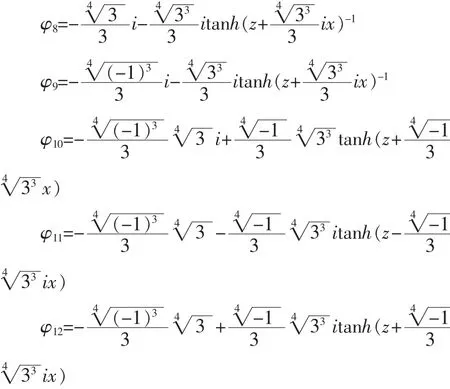
与D.Anderson用变分法求解的结果比较发现，D. Anderson研究了光脉冲在光纤中的非线性传播的传输方程，假设输入脉冲为，经过传输介质后光脉冲假定形式为（x））+ib（x）τ2）通过变分分析，D.Anderson得到了Ax、a（x）、b（x）的演化关系，能很好地分析光脉冲的演化情况，而本文通过tanh-coth方法得到了一系列的具体的解，这对问题的分析有更好的指导作用。

3　结语

本文运用tanh-coth方法求出了简化的光束在弱调制情况下的传输方程的解析解，通过求解过程可以看出tanh-coth方法解非线性方程十分的简洁，易懂，直观，而且能够得到十分丰富的解的数据，能够帮助我们更好地分析和研究相关的非线性方程。

［1］廖欧，舒级，曾群香.一类混合KDV方程的精确孤立波解［J］.四川师范大学学报：自然科学版，2015（4）：493-496.

［2］董孝义.光孤子通信原理与进展［J］.光通信技术，1992，16（2）：28-39.

［3］Ablowitz M J，Segur H.Solitons and Inverse Scattering Transform［M］.Philadelphia：SIAM，1981.

［4］楼森岳.推广的Painlevé展开及KdV方程的非标准截断解［J］.物理学报，1998，47（12）：1937-1945.

［5］张解放，郭冠平.（2+1）维破裂孤子方程的新多孤子解［J］.物理学报，2003，52（10）：2359-2362.

［6］Anderson D.Variational Approach to Nonlinear Pulse Propagation in Optical Fibers［J］.Physical review A，1983，27（6）：3135.

［7］Gzükizil F，Salhi A.New Travelling Wave Solutions of Two Nonlinear Physical Models by Using a Modified Tanh-Coth Method［J］. Journal of Algorithms&Computational Technology，2015，9（1）：1-12.

The tanh-coth Solution to the Beam Nonlinear Transmission Equation

XU Wei-jin，ZHUO Hui
（Institude of Information and Science Technology，Hunan Agriculture University，Changsha 410128）

Analyzing the analytic solutions of Nonlinear Schrodinger equation plays a significant role in studying the transmission of information.Uses the tanh-coth method to solve Nonlinear Schrodinger equation and gets a series of decent analytic solutions，which makes a positive difference in studying the nonlinear transmission.

Optical Soliton；Nonlinear Schrodinger Equation；tanh-coth Method

1007-1423（2016）23-0013-03DOI：10.3969/j.issn.1007-1423.2016.23.003

徐伟津（1994-），男，湖南永州人，学生，专业方向为主攻非线性传输

卓辉，博士，副教授，研究方向为从事光的非线性、光孤子等理论，E-mail：zhuohuitxh@163.com

2016－05－10

2016－08－05