基于改进CRITIC权的灰色关联评价模型及其应用
2016-10-26王磊高茂庭
王磊,高茂庭
(上海海事大学信息工程学院,上海201306)
基于改进CRITIC权的灰色关联评价模型及其应用
王磊,高茂庭
(上海海事大学信息工程学院,上海201306)
为了改进灰色关联分析模型评价精度低的缺点,将CRITIC算法与灰色关联分析方法相结合,并根据实际,建立起基于改进CRITIC权的灰色关联分析评价模型。采用CRITIC法确定指标权重,不仅克服传统灰色关联分析中多采用主观赋权法的不确定性,而且与常用客观赋权法相比,CRITIC在考虑指标变异性大小的同时兼顾指标之间的相关性,因而更具客观性。模型在城市雨水资源开发利用潜力综合评价中的分析结果表明:将CRITIC理论引入到灰色关联分析模型中是科学的,所建立的模型是合理的,能够提高灰色关联分析模型的评价精度。
CRITIC;灰色关联分析;综合评价
0 引言
对城市区域雨水资源开发利用情况进行综合评价,不仅可以对雨水资源的利用情况进行深刻的认识,而且可以对本市不同区域的雨水资源利用情况进行对比,找出存在的问题,另外,对城市的区域的规划有一定的指导意义。
目前,对城市区域雨水资源开发利用情况的综合评价方法,主要有主观评价法和客观评价法。常用的主观评价法如模糊综合评价法[1]和层次分析法[2],它们主观性太强,当待评价对象的指标数目过多时,会对决策者带来极大的工作压力;常用的客观评价法如因子分析法[3]、物元分析法[4]和灰色关联分析法(Grey Relational Analysis,GRA)[5]等。因子分析法比较适合多样本的情况,对小样本会产生很大误差;物元分析法算法比较复杂,不易理解;而灰色关联分析法计算简单,而且,对小样本不敏感的特性使其很适合对城市区域雨水资源开发利用进行综合评价。故本文采用灰色关联分析法对城市区域雨水资源开发利用进行综合评价。
常见的指标的权重确定方法有两类:主观确定法和客观评价法。常见的主观法有层次分析法[6]和德菲尔法[7],这些方法会造成评价结果可能由于人的主观断定而形成偏差;常见的客观评价法有标准离差法[8]、变异系数法[9]和熵权法[10]。这些方法的共同特点是,根据已有观测数据来计算某一指标的差异程度,差异程度越大,该指标的权重越大。它们在一定程度上反映了各个指标之间的权重关系,然而这些客观评价方法仅仅考虑了指标内部之间差异性对权重的影响,而没有考虑到指标间的影响。特别是当所选取的指标间关联性过高时,用以上方法所确定的权重精度会很低。
本文引入CRITIC法[11]来确定指标权重。CRITIC法不仅考虑到指标内部变异程度对指标权重的影响,而且考虑了指标之间的冲突性。特别是当指标选取的时候关联度过大时,可以在正相关程度较高的指标中去点一些指标,使得权值的确定更加合理。
1 理论概述
1.1GRA法
GRA法是灰色理论最重要的方法之一。通过计算样本序列与参考序列的灰色关联度,可以确定样本与参照者之间的关联程度,并根据这种程度的大小,来确定各种待评价样本的先后次序。GRA法建模具体步骤如下[5]:
(1)确定参考序列和比较序列
设实测样本序列数即参考序列有m个,包含n个评价指标,则第i实测样本序列:
Xi={xi(1),xi(2),…,xi(n)},i=1,2,…,n(1)
设分级标准作为比较序列,共分s级,因此有第j级标准的参考序列:
Yj={yj(1),yj(2),…,yj(n)},j=1,2,…,s(2)
(2)变量的标准化
在进行灰色关联度分析时,一般都要进行标准化处理:
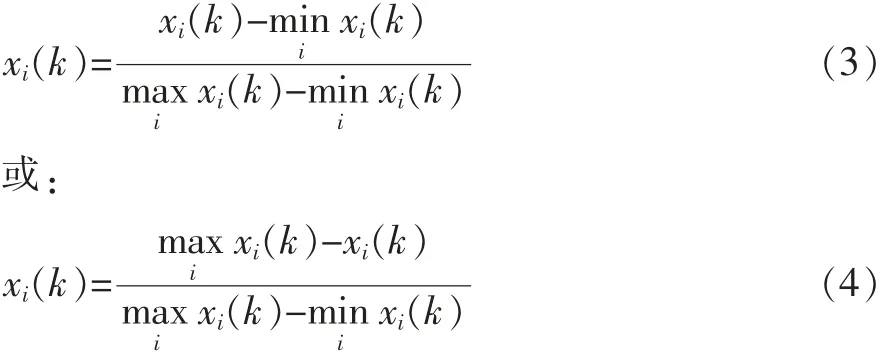
式(3)、(4)中,xi(k)表示标准化后第i个样本的第k个指标值,i=1,2,…,m;k=1,2,…,n。式(3)适用于效益型指标,即值越大效用越好;公式(4)适用于成本型指标,即值越小效用越好。
(3)求关联系数
设aij(k)为关联系数,则:

式(5)中:k=1,2,…,n;Δij(k)=|xi(k)-yj(k)|为{xi(k)}与{yj(k)}在第i点与第k项的绝对差;Y为分辨系数,其取值在0~1之间,一般取Y=0.5;Δmax为二级最大差,Δmin为二级最小差,其值分别为:

(4)确定各指标的权重
主要有主观赋权法和客观赋权法,可以根据不同的应用场景,选择合适的方法。最后得出n个评价指标的权重为:ω(k),k=1,2,…,n。
(5)求加权关联度

式(8)中:ω(k)为第k指标权重,k=1,2,…,n。
对于某一个实测评价样本,通过对该参考序列加权关联度大小的比较,得到Vmax,即可确定该实测评价样本所属的等级。然后根据不同实测评价样本序列与比较序列即标准序列比较所得Vmax,可以对评价样本进行排序,从而实现排序和等级分类。
1.2CRITIC法
CRITIC法运用评价指标内部的对比强度与指标之间的冲突性的乘积来综合衡量指标的客观权重。
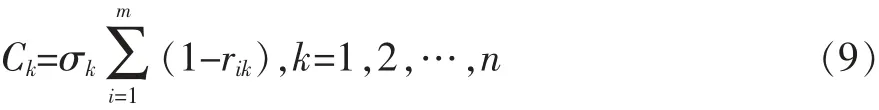
设Ck表示第k个评价指标所包含的信息量,则Ck可表示为:式(9)中,σk是第k个指标的标准差,rik是评价指标i和k之间的相关系数。
Ck越大,表示第k个指标所包含的信息量越大,所以第k个指标的客观权重ω(k)应为:
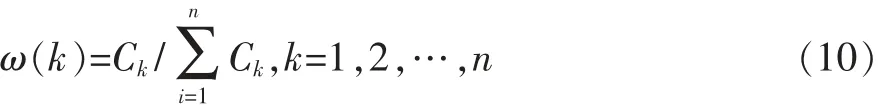
2 基于改进CRITIC权的灰色关联模型的建立
本文根据灰色关联分析理论和CRITIC法,建立起基于CRITIC权的灰色关联模型,模型建立步骤如下:
(1)根据应用场景来确定比较序列和参考序列;
(2)根据式(3)、(4)将样本进行标准化处理;
(3)求关联系数aij(k)。
①Δij(k)的确定
一般情况下,若参考序列是具体数据时,可以由式(5)知Δij(k)=|xi(k)-yj(k)|。但是如果参考序列的指标并非唯一的具体数据,而是一个区间时,需要用新的计算方法来确定Δij(k)。
此时设参考序列区间yj(k)=[aj(k),bj(k)],则有:
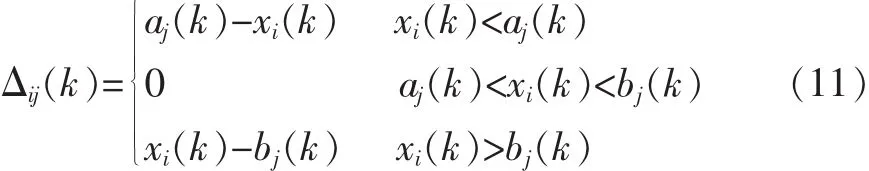
式(11)中:aj(k),bj(k)分别表示指标k在第j个级别上的上限与下限。
②分辨系数的确定
根据文献[12]可知,分辨系数Y是二级最大差(maix makxΔij(k)的重要程度的度量。它的取值规则如下:
记为所有差值绝对值的均值,即:

并记XΔ=Δv,则Y的取值为:XΔ<Y<2XΔ,并且满足:
当Δmax>3Δv时,XΔ<Y<1.5XΔ(13)
当Δmax≤3≤Δv时,1.5XΔ<Y<2XΔ(14)
(4)用改进的CRITIC法确定权重
①确定判断矩阵R
R=(xij)mn(i=1,2,…,m;j=1,2,…,n)(15)
②对R进行归一化,得归一化阵B=(bij)mn(i=1,2,…,m;j=1,2,…,n):

式(16)中:xmax,xmin分别为同一参考指标中的最优者和最差者。
③计算指标内的对比强度
按照CRITIC方法,对比强度由标准差来确定,但如果各个指标下的数据的平均数不同时,对比强度使用标准差法就变得不太合理。本文在确定指标内对比强度的时候对CRITIC方法进行改进,采用变异系数来作为对比强度的度量。消除各指标间均值不相等所造成的误差。则对比强度Cv(k):
Cv(k)=σ(k)/μ(k)(17)
式(17)中,σ是第k个指标的标准差,μ(k)是第k个指标的均值。
④计算指标间的冲突性
指标k与其他指标的冲突性为Cf(k):

其中rik是评价指标i和k之间的相关系数。
⑤确定信息量
根据步骤③和步骤④可知,改进CRITIC法后所确定信息量Ck':
Ck'=Cv(k)Cf(k),k=1,2,…,n(19)
⑥确定权重
最终,在改进后的算法所确定的权值为:
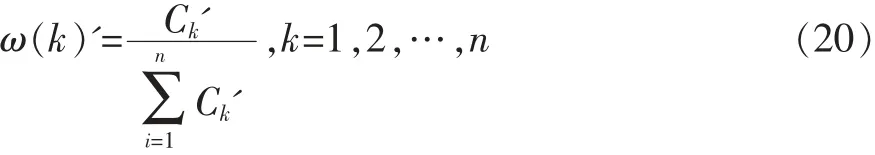
(5)求加权关联度
根据步骤(3)得到的关联系数aij(k),与步骤(4)得到的权重ω(k)来确定加权关联度:

3 应用实例
本文将基于改进CRITIC权的灰色关联评价模型应用到城市雨水资源开发利用潜力的综合评价当中,为了便于对比,本文采用文献[1,2,5]中的样本数据。
3.1评价指标的确定
影响区域雨水开发利用的因素主要有雨水资源控制率I1、农业灌溉用水中雨水所占比例I1、生活用水中雨水所占比例I3、工业用水中雨水所占比例I4和工业用水中雨水所占比例I5。各评价指标的数值见表1。
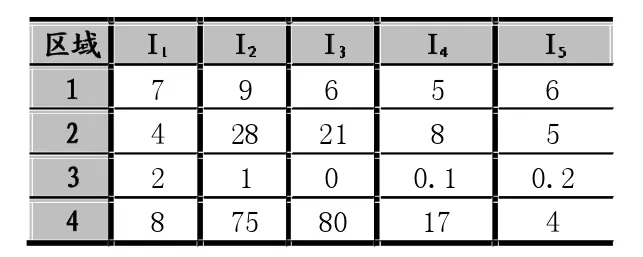
表1 各区
3.2雨水资源开发利用潜力分级
雨水资源开发利用潜力可分为三个阶段:即初始阶段V1、发展阶段V2和饱和阶段V3。具体标准见表2。

表2 综合评价指标分级值%
3.3雨水资源开发利用潜力综合评价
(1)确定参考序列和比较序列
在该应用中,样本序列数有4个(区域1,2,3,4),包含5个评价指标(I1,I2,I3,I4,I5),则实测样本序列矩阵X:

本应用中,分级标准作为比较序列,共分3级(V1,V2,V3),因此比较序列矩阵Y:
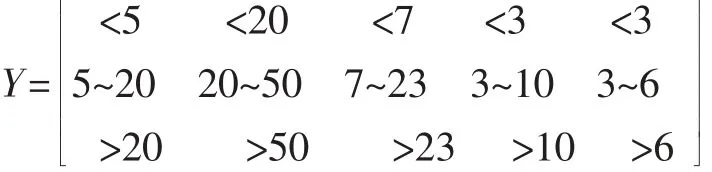
(2)变量的标准化
由于指标值和分级值都是相对数,具有相同的量纲,数量级相差不悬殊,从而不需进行标准化处理。
(3)求关联系数
根据公式(3)-(8)可以分别求得各个区域针对不同阶段的关联系数矩阵。
样本区域与阶段V1对应的关联系数矩阵A(V1):

样本区域与阶段V2对应的关联系数矩阵A(V2):


样本区域与阶段V3对应的关联系数矩阵A(V3):
(4)用改进的CRITIC法确定权重
根据公式(12)得4个事务(区域1,2,3,4),5个评价指标(I1,I2,I3,I4,I5)的判断矩阵R:

根据公式(13)得到归一化判断矩阵B:

根据公式(14)得,各指标间对比强度矩阵Cv(5)-R:
Cv(5)-R=[0.8473 1.2169 1.3676 0.9571 0.7042)]
根据公式(15)可得,各个指标之间的关联系数矩阵Cf(k)-R:
Cf(k)-R=[1.1868 1.0964 1.1688 0.8465 2.4130]

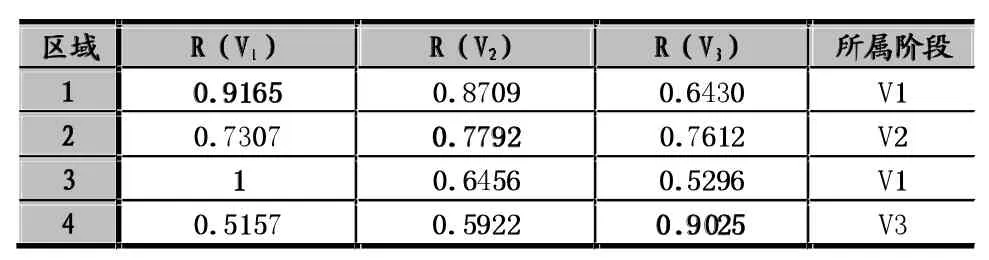
表3关联度计算评价结果
3.4雨水资源开发利用潜力综合评价
(1)与其他参考文献对比
根据表4和表5,对比各种方法的评价结果,可以看出:改进后的基于CRITIC权灰色关联分析的评价结果与参考文献[1]采用的模糊评价计算结果,文献[2]采用的基于AHP(层次分析法)权的灰色关联评价,以及笔者参考文献[13]而建立起的基于变异系数权的灰色关联评价模型的结果即区域水资源分级相同。
而本文中的方法与参考文献[5]所采用的基于熵权的灰色关联分析模型的结果有一定的出入。具体体现在针对区域四的评级,本文和其他文献一样,将区域四划分到V3阶段,而文献[5]却将区域四划分到V2阶段。
从理论层面上讲,基于信息熵的权重确定方法和其他客观评价方法一样,只考虑到了指标内部变异大小对权重的影响,而没有考虑到指标之间的冲突性。当两个指标的正相关程度较高而不采取一定的措施来消除相关性,会直接影响到权值的准确性。另外,在确定分辨系数的时候,文献[5]只是根据他人经验,定性的将分辨系数Y定为0.5。一般,该方法能解决一部分问题,但考虑到计算精度时,应当对Y定量分析,然后确定其值。参考表6可以看出:利用式(13)、(14),当与不同的评价指标进行灰色关联计算时,会产生不同的分辨系数,这种方法所获取的分辨系数更加合理。
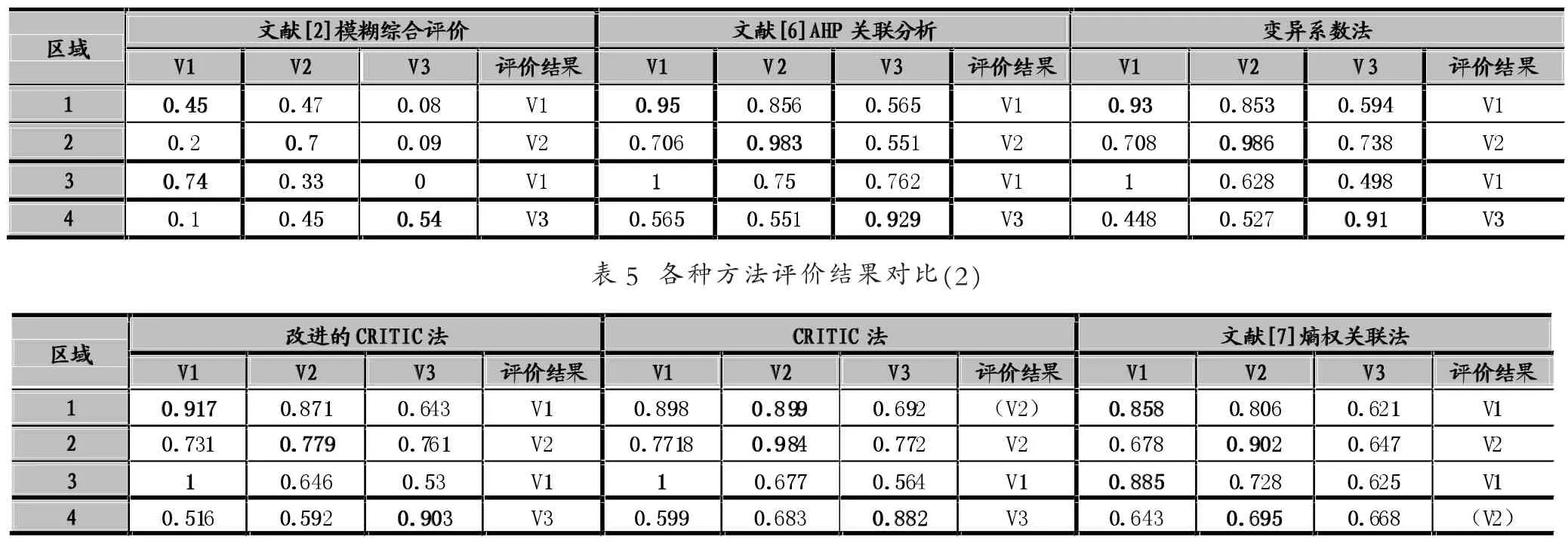
表4 各种方法评价结果对比(1)
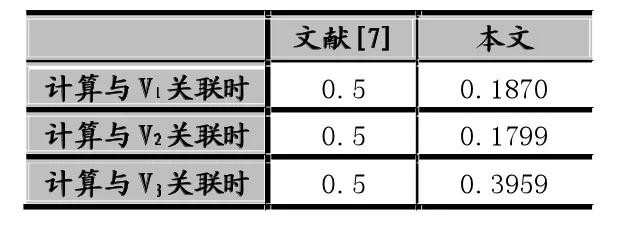
表6 分辨系数的取值
从实际情况来看,考察区域四与阶段的关联性,有三项指标I2,I3,I4,已经超过了比较序列V3的标准,指标I5也已经很接近了比较序列V3的标准。所以把区域四划归V3阶段更为合理。
(2)与改进前的CRITIC方法对比
参考表5,可以看出:改进的CRITIC权比原始的CRITIC权在最终的评价分级上有一定的出入。改进的CRITIC法把区域一划分到V1阶段,这与其他文献相同。然而,原始的CRITIC法却把区域一划分到V2阶段。
从理论上来讲,单纯的CRITIC权在计算指标内部的对比强度时,利用标准极差法,而本文运用的是变异系数法。虽然两种方法确定对比强度的原理相同,即通过变异程度来确定信息量,变异程度越大,说明该包含的信息量越多,从而该指标的重要性(权重)相应会高一点。然而由变异系数法的定义可知:
若两个指标的样本平均数和量纲一致时,可以直接通过他们指标上数据的标准差作为衡量这两个指标变异程度的度量,但是,当他们的量纲或者平均数不一致时,仅仅依靠标准差来度量差异程度会产生很大误差,此时应当需采用标准差与平均数的比值即变异系数来确定差异程度。而本文中,虽然对各个指标进行了无量纲化处理,但各个区域在各个指标上的平均数并不相同,因此在确定指标的对比强度时,利用变异系数法比利用标准差法更为合理。根据表7,可以看出,单纯的CRITIC权法和其他赋权法相比,它给指标I5异常高的权重,而本文所提出的基于变异系数的CRITIC权可以降低指标I5的重要程度。
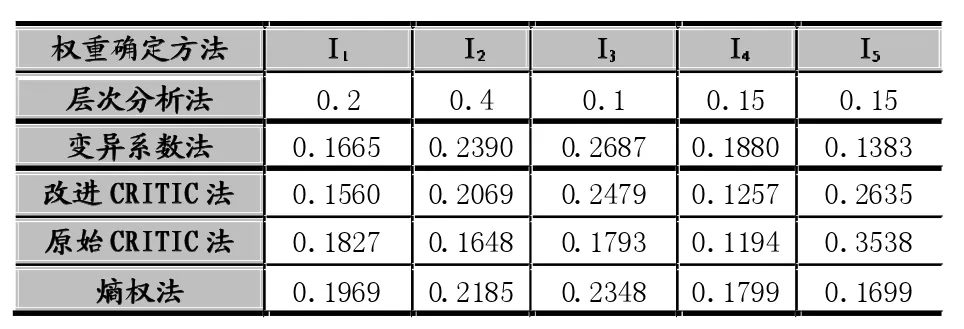
表7 不同权重确定方法的确定结果
结合实际,根据表1和表2可以看出,区域一两项指标I2,I3在达到V1的标准。虽然区域一在指标I1上达到V2标准,但只是在区间上一小部分的达到,直观上看,该指标划归V2的概率小于划归V1的概率。同理,区域一在指标I4上标划归V2的概率小于划归的V1概率。因此把区域一划归V1更为合理。
4 结语
在灰色关联分析中引入CRITIC理论,克服了传统客观评价法如标准离差法、变异系数法、熵值法等无法解决指标之间的冲突性对权值的影响,使评价结果更符合实际。本文实验表明:基于改进CRITIC权的灰色关联分析方法不仅可行,而且结果更加合理。评价结果与文献[1]、[2]和[5]基本一致,不一致主要体现在对权值的确定时,熵权法没有考虑到指标之间的冲突性,值得我们进一步研究和探讨。
[1]陈卫宾,徐建新,张亮.区域雨水资源开发利用潜力综合评价[J].灌溉排水学报,2004,23(05):66-68.
[2]徐建新,郭文献,卢双宝.区域雨水资源开发利用潜力的灰色关联分析与评价[J].灌溉排水学报,2005,24(03):50-52.
[3]孙洪哲,王晓楠,杜涓.基于因子分析法的河北省公共服务绩效评价体系研究[J].河北工程大学学报:社会科学版,2015(4):6-8.
[4]宋士强,王明刚,李春莲,等.基于物元分析法的雨水资源开发评价[J].中国水运月刊,2009,9(1):179-181.
[5]李国良,付强,孙勇,冯艳.基于熵权的灰色关联分析模型及其应用[J].水资源与水工程学报,2006(06).
[6]姜灵敏,肖金森,钟瑞琼.基于Borda序值法和模糊层次分析法对跨国公司R&D外包的风险度量[J].价值工程,2016(1):79-81.
[7]李沛丽,张华,李涛,等.德菲尔法构建重大动物疫病预警指标体系[J].中国动物检疫,2016,33(3):77-80.
[8]罗京亚,罗爱静,谢文照,等.基于标准离差法与TOPSIS法的中药知识产权评价体系的构建[J].中华医学图书情报杂志,2015(05):2-6.
[9]向泉,罗金耀,李小平,等.基于博弈论法确定小农水项目绩效评价指标的权重[J].中国农村水利水电,2016(6).
[10]何卫平,赵继宗.基于熵权法的甘肃省科技发展水平实证研究[J].开发研究,2016(2).
[11]刘俊娥,毕明杰,郭章林.CRITIC—优度评价法在建筑工程施工评标上的应用[J].建筑安全,2016,31(4):33-37.
[12]吕锋.灰色系统关联度之分辨系数的研究[J].系统工程理论与实践,1997,17(06):49-54.
[13]赵宏,马立彦,贾青.基于变异系数法的灰色关联分析模型及其应用[J].黑龙江水利科技,2007(02),
Grey Relational Evaluation Model Based on Improved CRITIC Weight and Its Application
WANG Lei,GAO Mao-ting
(College of Information Engineering,Shanghai Maritime University,Shanghai 201306)
In order to improve the accuracy of grey relational analysis model,combines the CRITIC algorithm with grey relational analysis,and establishes the grey relational analysis model based on the improved CRITIC weight.Uses CRITIC method to determine the index weight,not only overcomes the traditional gray correlation analysis in the use of subjective weighting method,and compares with the commonly used objective weight method,CRITIC in the consideration of the index variation of the correlation between the indicators,and therefore more objective.The analysis results of the model in the evaluation of regional rainwater resources development and utilization potential of the comprehensive evaluation show that the CRITIC theory is scientific,and the model is reasonable,and can improve the accuracy of gray correlation analysis model.
CRITIC;Grey Relational Analysis;Comprehensive Evaluation
1007-1423(2016)23-0007-06DOI:10.3969/j.issn.1007-1423.2016.23.002
王磊(1990-),男,河南邓州人,在读研究生,研究方向为数据挖掘、云计算
2016-05-13
2016-08-13
高茂庭(1963-),男,博士,教授,系统分析员,CCF高级会员,研究方向为智能信息处理、数据库与信息系统
