求解含小阻抗支路配电网潮流的牛顿法

初　壮，于群英，李笑薇

（1.东北电力大学电气工程学院，吉林 132012；2.国网吉林省电力有限公司电力科学研究院，长春130000；3.吉林省送变电工程公司，长春 130000）

求解含小阻抗支路配电网潮流的牛顿法

初壮1，于群英2，李笑薇3

（1.东北电力大学电气工程学院，吉林 132012；2.国网吉林省电力有限公司电力科学研究院，长春130000；3.吉林省送变电工程公司，长春 130000）

基于节点导纳矩阵的雅可比矩阵为病态，是采用牛顿法求解含合环支路等小阻抗支路的配电网潮流不易收敛的主要原因。文中以等效负荷支路、合环支路分别为连支建立两类基本回路，潮流方程基于回路电流-负荷节点电压方程建立，合环支路参数不会作为回路矩阵的独立元素存在；采用牛顿法求解时，基于回路导纳矩阵建立良态的雅可比矩阵，使计算收敛性得到保证。多个算例验证了该方法在计算含合环支路和PV节点配电网潮流时的正确性和有效性。

配电网潮流计算；收敛性；回路分析；牛顿法；小阻抗支路

典型的传统配电网是单一电源供电的辐射状网络。而现代配电网构成日趋复杂：风力、光伏发电等分布式电源的大力发展改变了配电网单一电源供电模式［1-6］；而实际运行时会出现闭合分段开关和联络开关的情况，使配电网呈现为弱环网［6］。潮流计算是电力系统运行分析的基础，配电网潮流计算需要面对这些新问题。前推回代法在求解传统配电网潮流时具有简捷、高效的特点，但不能直接用于弱环网或电网具有PV节点的情况。因此，文献［7-8］采用叠加原理来处理环网问题，文献［5-6］在迭代中采用不同方法对PV节点进行电压修正。这些修正使前推回代算法的效率有所降低。

牛顿法易于处理多电源节点和复杂网络结构，广泛用于输电网潮流计算；但配电网潮流采用牛顿法时，网络中合环开关等小阻抗支路［9］的存在使算法收敛性有很大程度下降。对牛顿法计算含小阻抗支路的输电网潮流收敛性较差的原因与解决方法已有较多研究：文献［10-11］指出，小阻抗支路的存在使潮流方程雅可比矩阵呈现病态，使迭代过程不收敛；文献［10］指出提高程序计算精度可以提高算法收敛性；文献［11］通过改变迭代过程电压初值提高收敛性；文献［12］则采用线性变换对雅可比矩阵进行预处理等。配电网多呈辐射网或弱环网运行，R/X较大，小阻抗支路数量要多于输电网，这些特点使牛顿法在计算基于节点形式潮流方程时更加不易收敛［9］。

本文采用牛顿法计算基于回路形式配电网潮流方程。采用回路形式潮流方程，不但可有效处理弱环网，更重要的是可避免出现病态的雅可比矩阵；牛顿法的应用则使算法可直接用于含PV节点的配电网，对含分布式电源配电网有良好的适应性。

1　基于回路分析的配电网潮流方程

1.1回路的形成和分类

对于带有环路的配电网，按如下规则建立回路电流方程：断开形成环路的支路，则配电网呈辐射状，此时，将各节点负荷或分布式电源视为接地支路，则自根节点至负荷节点或分布式电源所在节点的对地支路可形成回路，取回路电流为负荷节点或电源节点对地的注入电流，称其为第1类回路；取回路电流为负荷节点对地的注入电流，对应的回路方程称为第1类回路方程；将形成环路的支路接入配电网，则自根节点至该支路一个关联节点、经由该支路至另一关联节点并由另一节点回溯至根节点也会形成回路，称其为第2类回路；取回路电流为环路支路电流，方向规定为由节点编号大的节点指向编号小的节点。

配电网辐射状运行时，各线路皆为树支，而节点负荷投入或合环支路闭合则会使配电网中出现回路；负荷等效支路、合环支路都是连支，但它们性质不同，因此，把由它们的出现而产生的回路分别定义为第1类和第2类回路。

例如，图1是一个8节点（未计入接地点）、9条支路的配电网络，其中支路b11、b12是合环支路。另外，有1、3、6共3个节点接负荷，可看作3条支路b8、b9、b10；根节点与接地节点之间可看作为一条电压源支路，记为b0。通常的配电网络的支路概念中不含b0、b8、b9、b10这些支路。

对应支路b8、b9、b10，有3个第1类回路：

loop 1-1：b0-b1-b3-b6-b8；

loop 1-2：b0-b1-b4-b7-b9；

loop 1-3：b0-b2-b5-b10。

对应两个合环支路b11、b12，有两个第2类回路：

loop 2-1：b3-b11-b4；

loop 2-2：b1-b12-b2。

然后，消去第2类回路（下文详细说明），可以得到关于1、3、6共3节点的方程，求取得到带有负荷节点的参数，然后根据支路方程求取不带负荷节点的参数，进而得到所有节点参数。同样，对于8节点系统，如果每个节点都带有负荷，则经消去第2类回路可建立含有8个方程的方程组，可直接求出每个节点的参数。

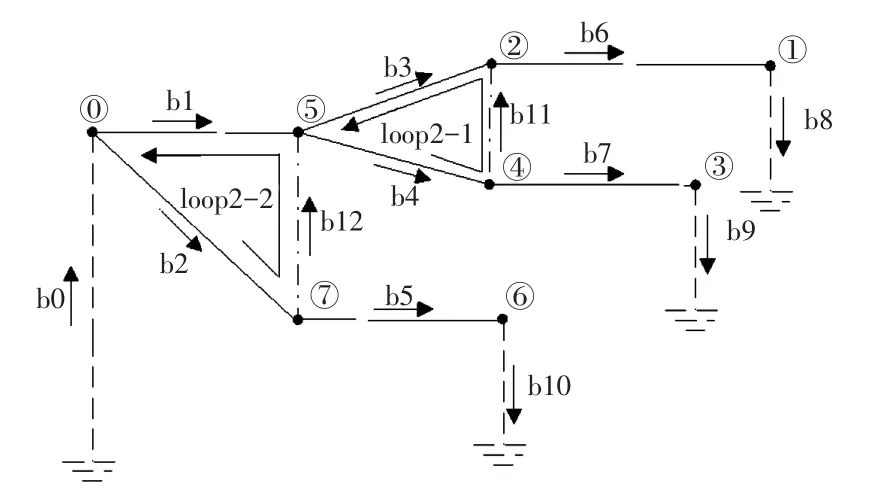
图1　两类回路的划分Fig.1 Two types of loops

1.2分布式电源的处理

目前，比较成熟的分布式电源主要有光伏、风力发电机、燃料电池、微型燃气轮机。对于光伏可根据其无功功率与有功功率、电流、节点电压的关系，将其转化成PQ节点处理［4］；双馈风力发电机可直接等效成功率方向相反的负荷；而对于燃料电池，微型燃气轮机，在潮流计算时会被处理成PV节点［4］。对于PV节点来说，无需计算关于其无功功率的方程式，其有功功率的不平衡量以及对应的雅可比矩阵元素与PQ节点相同。

1.3回路方程的建立

本文中将第1类回路方程连续排列在先，第2类回路方程连续排列在后，则回路电流方程写为

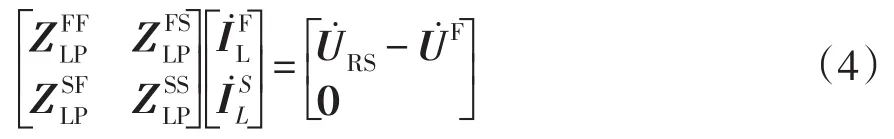
消去第2类回路对应各行，回路方程变为

方程（10）消去了第2类回路对应的方程，方程个数为第1类回路个数，即负荷节点及分布式电源节点的总数。这样处理的优点在于，虽然第2类回路的出现会使回路方程数量增多，但在进一步建立潮流方程之前将其等值，使回路方程规模与第2类回路出现前相同，不会增加潮流计算的计算量。

另一方面，由两类回路的定义可见，即使合环支路为小阻抗或零阻抗支路，因其不在第1类回路中，也不会是第1、2类回路之间的互阻抗，不会对第1类回路产生影响；而第2类回路自阻抗则至少含有两个正常阻抗支路，也不会出现过小的情况。

2　基于回路方程的配电网潮流计算

2.1基于回路分析的潮流方程

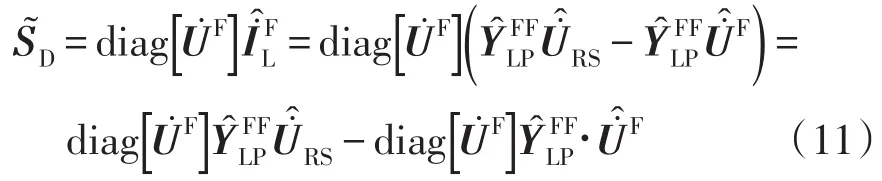
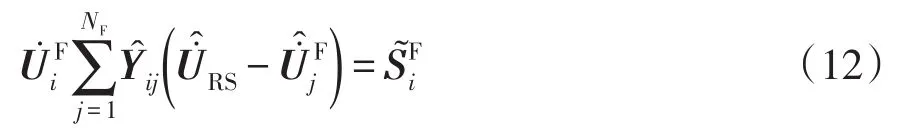
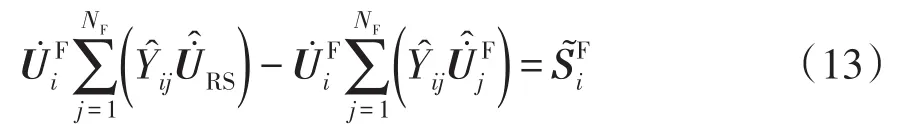
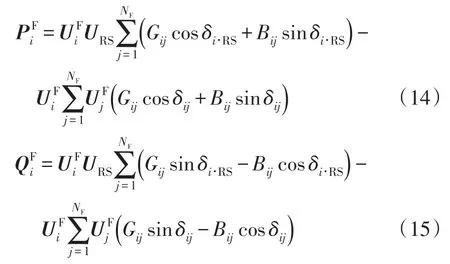
式中：δi·RS为节点i电压相量与根节点电压相量的相角差；δij节点i、j电压相量的相角差。节点注入功率不平衡量为

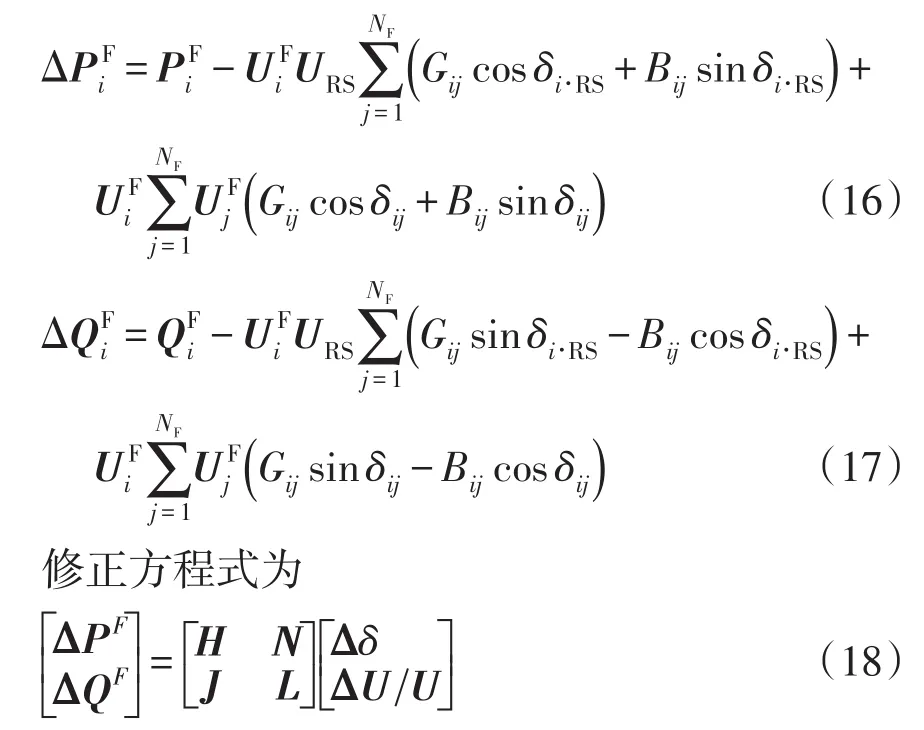
4个子矩阵H、N、J、L构成了修正方程式的雅可比矩阵。当i≠j时，雅可比矩阵的各个元素分别为

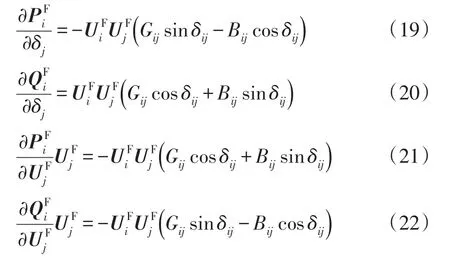
δj为节点 j电压相量与参考节点电压相量的相角差。当i=j时，雅可比矩阵的各个元素分别为

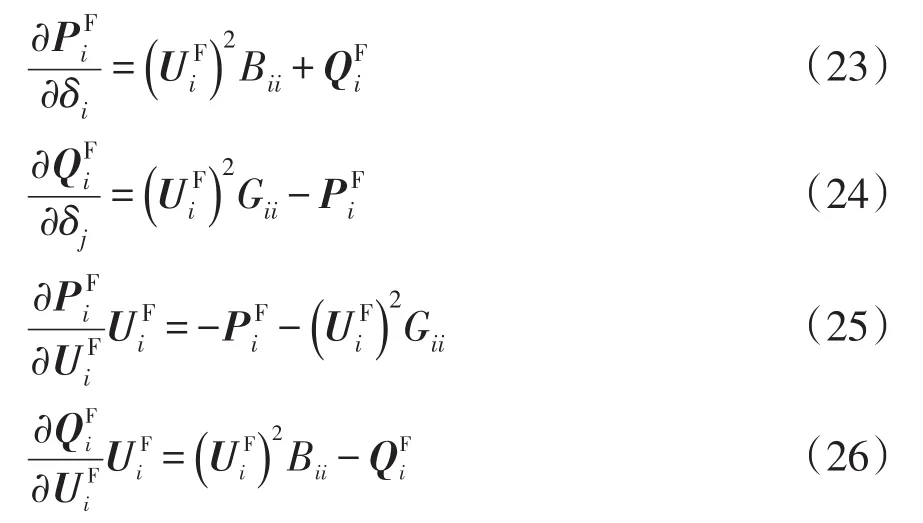
2.2牛顿法潮流计算步骤

在建立式（14）、（15）形式的潮流方程后，采用牛顿法求解，求解过程与采用牛顿法求解节点形式潮流方程基本相同，其步骤简述如下。

（1）读取系统原始数据，形成支路阻抗矩阵，根据回路与支路阻抗矩阵的关系，求取回路阻抗的矩阵；

（2）根据式（6）～（8）消去第2类回路，求出等效回路导纳矩阵；

（4）将各节点电压的初值代入式（16）、（17）求出功率不平衡量

（5）将各节点电压的初值代入式（19）～（26），求出雅可比矩阵的各个元素

由1.1小节建立回路方程的分析可知，潮流计算收敛后可直接得到负荷节点电压列向量和第1类回路的回路电流列向量；由1.3节式（4）可得第2类回路的回路电流列向量为

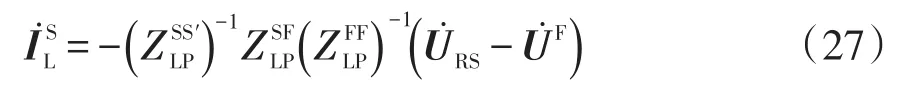
3　线性方程组系数矩阵的条件数

无论采用节点方程形式，还是采用回路方程形式，牛顿法中求解的修正方程都是一个以潮流方程雅可比矩阵为系数矩阵的线性方程组。

对于线性方程组的系数矩阵A，其条件数为

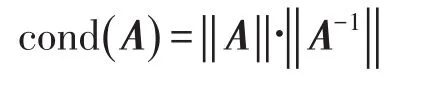
‖·‖为某种矩阵范数，如2-范数。由矩阵分析理论可知，系数矩阵的条件数可反映矩阵的非奇异程度。条件数越小，矩阵A的非奇异程度越高；条件数越大，A的非奇异程度越差，呈现“病态”。

对含小阻抗支路的电网络建立节点导纳矩阵并据此建立潮流方程，采用牛顿法求解，其迭代过程中的雅可比矩阵条件数非常大，矩阵为病态。数值计算时处理病态线性方程组的方法或是对系数矩阵进行预处理［12-14］，如文献［12］；或是采用更高的计算精度，如文献［10］所指出的那样。

对于同一电网络，根据2.2小节回路导纳矩阵建立的潮流方程，采用牛顿法求解，迭代过程中的雅可比矩阵条件数要小得多，非奇异程度高，对应的线性方程组收敛性好。因此，不必采用提高计算精度或对雅可比矩阵进行预处理等特殊方法处理小阻抗支路带来的收敛性问题。

在下文第4.1小节中，分别计算了节点形式和回路形式两种潮流方程迭代过程中雅可比矩阵的条件数，用来反映潮流方程的病态程度。

4　算例分析

基于Matlab R2010a实现下文所用各方法，各算法都采用双精度数据类型，允许误差设为1×10-6。采用本文回路形式潮流牛顿法对IEEE33节点系统［8］、PG&E69节点系统［15］及文献［7］的90节点系统进行计算，计算均能可靠准确收敛，表明了本文算法的正确性。下面分别从迭代次数、雅可比矩阵的条件数、处理环网能力及处理PV节点几个方面进行分析。

4.1迭代次数

表1中对比了本文算法（算法1）与直接法（算法2）、电流前推回代法（算法3）、传统节点形式潮流方程牛顿法（算法4）迭代次数。

表1　4种算法潮流迭代次数比较Tab.1　Comparison of the number of iterations among four kinds of algorithms

由表1可见，对于文献［7］的90节点系统，传统牛顿法由于受到小阻抗支路的影响不收敛；本文算法通过建立回路方程，避免了求取节点导纳矩阵，取而代之的是回路导纳矩阵，算法收敛。从表中还可看出，对于含有PV节点的网络以及弱环网，本文算法收敛所需迭代次数与算法4收敛时相同，明显少于算法2与算法3。

4.2雅可比矩阵条件数

采用牛顿法求解文献［7］的90节点系统的节点形式潮流方程不收敛，而牛顿求解本文回路形式潮流方程则是收敛的。表2给出了两种算法下前五次迭代过程雅可比矩阵的条件数。由表2可见，前者迭代过程中的雅可比矩阵条件数很大，非奇异程度很差，相应线性方程组呈现病态，因此迭代不收敛；而后者雅可比矩阵条件数相对很小，非奇异程度较好，迭代5次后收敛。

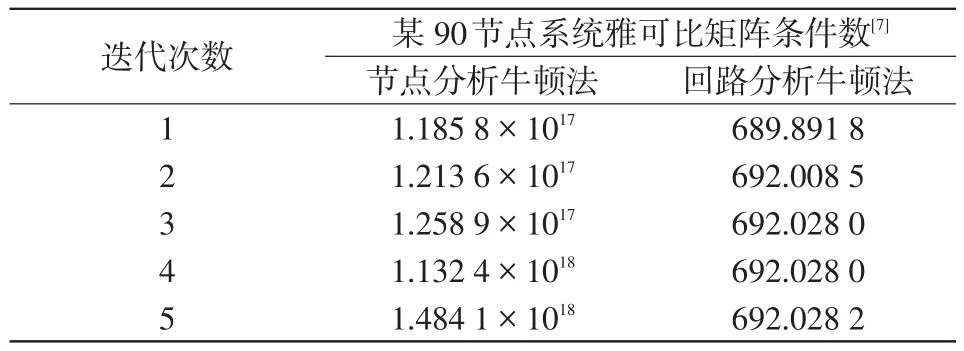
表2　两种算法关于雅可比矩阵条件数的比较Tab.2　Comparison of Jacobian condition number between two algorithms

4.3环网数对收敛性的影响

表3是在IEEE33节点系统加入了合环支路，考察本文算法处理环网的能力。可见，随着环网个数的增多，迭代次数并无明显变化；算例表明本文算法具有较强的环网处理能力，计算弱环网潮流时稳定性更高，收敛效果更好。

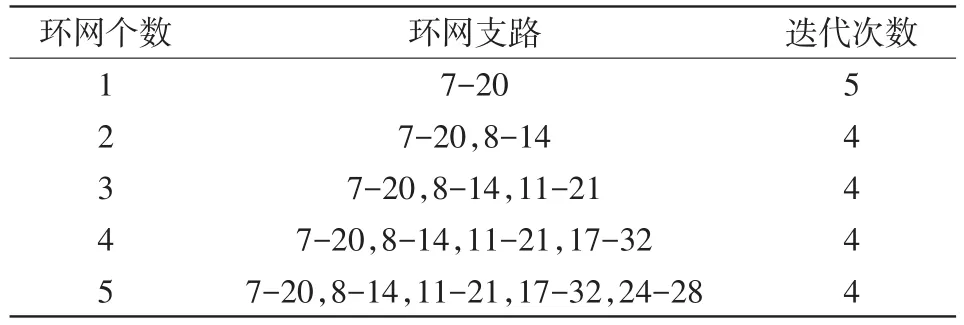
表3　环网个数对IEEE33节点系统收敛影响Tab.3　Impact of the number of meshes on convergence of IEEE 33-node system

4.4PV节点数对收敛性的影响

表4反映了采用本文模型与方法计算IEEE33节点系统含有分布式电源节点为PV节点的情况。可见，迭代次数并未随着PV节点接入个数的增多而增多。算法把根节点作为平衡节点，其他分布式电源作为PV节点。牛顿法处理PV节点的高效特性是直接阻抗法和前推回代法等支路法无法达到的。

表4　PV节点个数对IEEE33节点系统收敛影响Tab.4　Impact of the number of PV nodes on convergence of IEEE 33-node system

5　结论

本文建立了基于回路形式配电网潮流方程，并采用牛顿法进行求解。与传统方法相比，除了可以用于含分布式电源这一特点外，本文方法还具有以下特点：

（1）采用回路分析，能高效处理弱环配电网的潮流计算问题，不需在迭代计算中采用补偿方法计算环路电流，方程数即为负荷及电源节点数，环路支路不影响方程组规模，也不会增加求解过程的计算量；

（2）采用牛顿法求解潮流方程，对PV节点的处理过程和能力与牛顿法求解输电网潮流的情况相同，因此，本文方法可直接用于求解含有分布式电源的配电网潮流计算；

（3）本文方法基于回路分析及回路矩阵，在网络中含有小阻抗支路时，迭代过程中的雅可比矩阵条件数较小，非奇异程度高，避免了采用节点分析与节点矩阵时“病态”雅可比矩阵的出现，收敛性较好。在基于节点导纳矩阵的潮流计算因小阻抗支路存在不易收敛的情形下，本文模型与算法是获得配电网潮流分布一个有效的替代解决方案。

回路导纳矩阵是一个满阵，而节点导纳矩阵则是一个稀疏矩阵。因此，基于相同规模的回路导纳矩阵和节点导纳矩阵的潮流计算迭代过程，前者的计算量要高于后者，这是回路方法的一个不足。但是，由于配电网的回路数要小于节点数，其回路导纳矩阵的规模也要小于节点导纳矩阵，这在一定程度上抵消了因回路导纳矩阵为满阵而带来的计算量的增大。

［1］王成山，李琰，彭克（Wang Chengshan，Li Yan，Peng Ke）.分布式电源并网逆变器典型控制方法综述（Overview of typical control methods for grid-connected inverters of distributed generation）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（2）：12-20.

［2］王进，刘娇，陈加飞，等（Wang Jin，Liu Jiao，Chen Jiafei，et al）.计及风电不确定性的配电网无功模糊优化（Research on reactive power fuzzy optimization of distribution network with wind turbines）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（6）：8-13.

［3］王建勋，吕群芳，刘会金，等（Wang Jianxun，Lyu Qunfang，Liu Huijin，et al）.含分布式电源的配电网潮流快速直接算法（Fast and direct power flow algorithm for distribution network with distributed generation）［J］.电力自动化设备（Electric Power Automation Equipment），2011，31（2）：17-21.

［4］付英杰，汪沨，陈春，等（Fu Yingjie，Wang Feng，Chen Chun，et al）.考虑分布式电源的配电网电压控制新方法（New method of voltage control considering distribution network containing distributed generation）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（6）：26-31.

［5］朱星阳，张建华，刘文霞，等（Zhu Xingyang，Zhang Jianhua，Liu Wenxia，et al）.考虑负荷电压静特性的含分布式电源的配电网潮流计算（Power flow calculation of distribution system with distributed generation considering static load characteristics）［J］.电网技术（Power System Technology），2012，36（2）：217-223.

［6］丁明，郭学凤（Ding Ming，Guo Xuefeng）.含多种分布式电源的弱环配电网三相潮流计算（Three-phase power flow for the weakly meshed distribution network with the distributed generation）［J］.中国电机工程学报（Proceedings of the CSEE），2009，29（13）：35-40.

［7］Chang Gary，Chu Shou-Yung，Hsu Ming-Fong，et al.An efficient power flow algorithm for weakly meshed distribution systems［J］.Electric Power Systems Research，2012，84（1）：90-99.

［8］车仁飞，李仁俊（Che Renfei，Li Renjun）.一种少环配电网三相潮流计算新方法（A new three-phase power flow method for weakly meshed distribution systems）［J］.中国电机工程学报（Proceedings of the CSEE），2003，23（1）：74-79.

［9］Goswami S K，Basu S K.Direct solution of distribution systems［J］.IEEE Proceedings C，1991，138（1）：78-88.

［10］Tylavsky D J，Crouch P E，Jarriel L F，et al.The effects of precision and small impedance branches on power flow robustness［J］.IEEE Trans on Power Systems，1994，9（1）：6-14.

［11］姚玉斌，鲁宝春，陈学允（Yao Yubin，Lu Baochun，Chen Xueyun）.小阻抗支路对牛顿法潮流的影响及其处理方法（A method to deal with the effect of small impedance branches to prevent divergence inNewton-Raphson load flow）［J］.电网技术（Power System Technology），1999，23（9）：27-31.

［12］胡博（Hu Bo）.大规模复杂电力系统并行潮流计算和并行可靠性跟踪研究（Parallel Algorithms of Power Flow and Unreliability Tracing for Large-Scale Complex Power Systems）［D］.重庆：重庆大学电气工程学院（Chongqing：School of Electrical Engineering of Chongqing University），2010.

［13］薛毅.数值分析与科学计算［M］.北京：科学出版社，2011.

［14］周硕，郭丽杰，吴柏生（Zhou Shuo，Guo Lijie，Wu Baisheng）.Jacobi迭代预处理中的条件数与迭代次数的关系（Relation between condition number and iteration degrees in Jacobi iteration pretreatment）［J］.东北电力学院学报（Journal of Northeast China Institute of Electric Power Engineering），2003，23（6）：57-60.

［15］王守相，王成山.现代配电系统分析［M］.北京：高等教育出版社，2007.

Newton Method for Solving Power Flow of Distribution Networks with Small Impedance Branches

CHU Zhuang1，YU Qunying2，LI Xiaowei3
（1.College of Electrical Engineering，Northeast Dianli University，Jilin 132012，China；2.Electric Power Research Institute，State Grid Jilin Electric Power Ltd，Changchun 130000，China；3.Jilin Province Transmission and Substation Engineering Company，Changchun 130000，China）

The non-convergence of Newton method for the power flow computation of distribution networks is mainly due to the ill condition of Jacobi matrix built on node admittance matrix.In this paper，two kinds of loops are defined by two kinds of links respectively，i.e.，equivalent branches of loads and branches for closing.The model of power flow is based on loop-current load-node-voltage equations，and the parameters of small impedance branches are not independent elements in the network matrix.Newton method is applied to solving the equations，and the Jacobi matrix based on loop-admittance matrix is well-conditioned，which ensures the convergence of computation.Different cases with branches for closing and PV nodes indicate the correctness and efficiency of the proposed method.

power flow computation of distribution networks；convergence；loop analysis；Newton method；small impedance branches

TM712

A

1003-8930（2016）09-0036-06

10.3969/j.issn.1003-8930.2016.09.006

初壮（1973—），男，博士，副教授，研究方向为电力系统运行分析。Email：chuzhuang@hotmail.com

于群英（1988—），男，硕士，助理工程师，研究方向为电力系统运行分析。Email：happy7998523@126.com

李笑薇（1988—），女，本科，助理工程师，研究方向为电力系统运行分析。Email：happy6181056@126.com

2014-09-25；

2015-11-30

国家高技术研究发展计划（863计划）资助项目（2014AA052502）