考虑实际运行数据的风电场稳态建模

王海明，韩肖清，田建艳，秦文萍，刘志娟，米晓东

（1.太原理工大学，太原 030024；2.忻州供电分公司，忻州 034000）

考虑实际运行数据的风电场稳态建模

王海明1，韩肖清1，田建艳1，秦文萍1，刘志娟1，米晓东2

（1.太原理工大学，太原 030024；2.忻州供电分公司，忻州 034000）

为建立准确的风电场稳态模型，该文分区域分析了风电机组的稳态运行特性，提出一种基于实测数据的三机等效风电场稳态建模方法。首先，分析了风电机组在4个不同运行区域的稳态输出特性；然后，根据风电场内各风电机组的实测风速，采用改进型最大树法将其分类，并建立各类机群的实际风速-功率特性曲线；最后，由风电机组各区域稳态输出特性建立各类机群的风速-功率分段函数关系。在此基础上，计算各类机群的等值风速，从而建立三机等效风电场稳态模型。仿真结果表明三机等效模型可有效提高风电场稳态建模的精度。

实测数据；三机；稳态模型；改进型最大树法；风速-功率特性曲线

随着风力发电技术的日益成熟，风力发电在电力系统中的比重也逐渐升高，其随机性、波动性以及不可控性给电力系统的可靠运行带来了一系列影响［1-3］，如电能质量、功率平衡和经济调度等。因此，需建立能够准确反映各风电机组实际运行特性的仿真模型［4-6］，分析风电场输出功率的波动性，为电力系统经济调度和改善电能质量提供参考依据。

建立反映风电场内各风电机组风速-功率函数关系的数学模型是风电场稳态建模的一个重要环节［7-8］。风电机组生产厂家不同，其输出特性也不相同，即便是来自同一厂家相同类型的风电机组由于各风电机组在风电场内安装位置的差异，其输出特性也各不相同。传统风电场稳态建模方法假设所有风电机组输入风速和输出功率近似相等，整个风电场的输出功率与风电机组台数成正比［9］，因此传统的风电场稳态建模方法不能准确地反映风电场的实际运行特性。目前，已有相关文献对风电场稳态建模进行了深入研究。文献［10］采用数理统计的方法分析了风电场中风电机组的运行数据，得出了风电机组的实测风速-功率特性曲线，并根据实测风速-功率特性曲线搭建了定速风电机组的仿真模型，但是并未研究变速恒频风电机组的仿真模型。文献［11］基于风电场内各风电机组实测数据采用K-means聚类算法对所有风电机组进行聚类划分，然后建立整个风电场的等效风速模型，从而得到风电场稳态模型，但未考虑各类机群运行特性的差异，建立各类机群的稳态模型。文献［12］根据风电场的实际运行数据采用数理统计方法得到了反映风电机组实际运行特性的风速-功率特性曲线，但其只选取了风电场58台风电机组中的6台进行仿真验证，不足以反映整个风电场的实际运行情况。

本文通过分析风电机组稳态运行特性，将风电机组稳态输出特性分为4个区域，根据某实际风电场各风电机组的实测风速数据，提出了一种改进型最大树法，对风电场一期34台风电机组进行了分类。采用数理统计的方法对各类机群分区域进行风速-功率特性分析，建立其风速和输出功率的分段函数关系，得到了该风电场的稳态等值模型。

1　风电机组运行特性

双馈风力发电机组的输出功率与风力机的运行特性密切相关，风力机是风力发电系统中进行能量转换的一个重要环节，它截获流动空气中的部分动能将其转换为机械能，然后经双馈发电机组转换为电能，从而实现风力发电。

由空气动力学理论可知，风力机的输入功率为

式中：ρ为空气密度；Sw为风力机叶片迎风扫掠面积；v为进入风力机扫掠面之前的风速（即未扰动风速）。

风力机不能完全捕获流经其扫掠面的风能，并且发电机不能将其捕获的机械能完全转换为电能，因此风电机组的输出功率P表示为

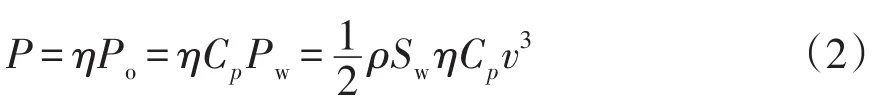
式中：Po为风力机输出的机械功率；η为风力发电系统的效率；Cp为风力机的风能利用系数。

式中：η1为机械传动装置效率；η2为双馈异步发电机组效率。

式（2）中，Cp反映了风力机捕获风能的能力，它与风速、风轮转速、风轮半径和桨距角有关，如式（4）和式（5）所示［13］。

式中：系数c1=0.517 6，c2=116，c3=0.4，c4=5，c5=21，c6=0.006 8；λ为叶尖速比；β为桨距角。

式中：ω为叶片旋转角速度；Dw为风轮直径。

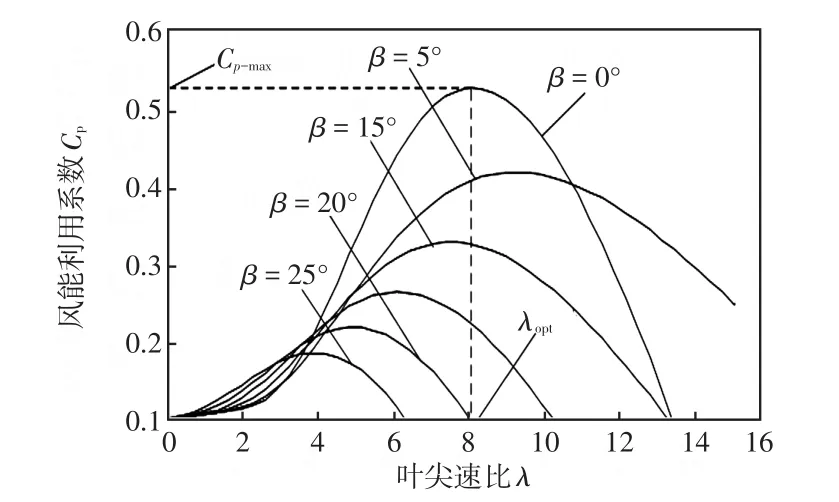
图1　风力机特性曲线Fig.1　Characteristic curves of the wind turbine

λ恒定时，Cp随着 β的增大而减小；β恒定时，存在一个最佳叶尖速比λ使得Cp最大。 β=0°时，对应的最佳叶尖速比λopt和最大风能利用系数Cp-max分别为8.1和0.48。

山西某实际风电场含有66台SL1500/82变速恒频双馈风电机组，具体参数如表1所示。该风电机组的风机类型为变速变桨距型，并配有自动偏航控制系统。

表1　风机参数Tab.1　Parameters of the wind turbine

变桨距风力机的输出功率不仅取决于叶片的气动特性，还取决于桨距角β的调节。在额定风速以下时，桨距角β为零（即β=0°），可看作定桨距风力机。在额定风速以上时，变桨距装置通过调节桨距角β保证发电机输出功率在允许的范围之内。根据不同风况，SL1500/82变速恒频风力发电机组运行于4个不同区域，4个运行区域的控制手段和控制目标各不相同。

（1）启动区（β=0°,3≤v＜4.5）

风速大于或等于切入风速时，通过调节风电机组的转速来尽可能多地捕获风能（如图1），调节发电机定子端电压实现并网操作。由式（4）计算风能利用系数Cp为

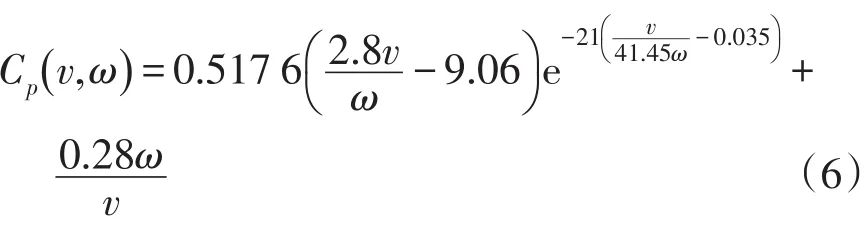
（2）最大风能追踪区（β=0°,4.5≤v＜9.5）

为了最大限度地捕获风能，风电机组的转速随着风速的变化而作相应变化，使风能利用系数Cp始终保持最大值Cp-max，该区域又被称为Cp恒定区。风能利用系数Cp计算如下：

（3）恒转速区（β=0°,9.5≤v＜10.5）

当风轮转速达到最大值17 r/min时，风电机组进入恒转速区，通过调节风电机组的输出功率来保持风电机组转速恒定。由式（4）计算风能利用系数Cp如下：

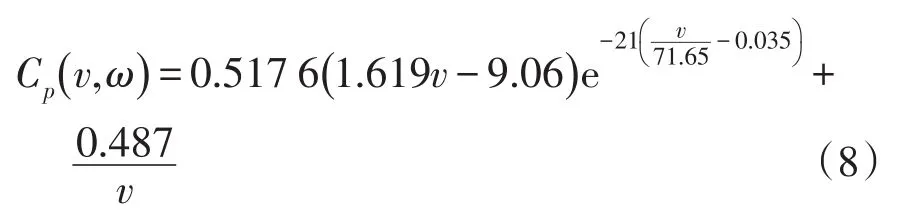
（4）恒功率区（β≠0°,10.5≤v≤25）

随着风速的不断增大，风电机组的输出功率达到最大值1 500 kW。通过风力机控制子系统来增大桨距角β使Cp迅速减小（如图1），从而保持风电机组输出功率恒定。风能利用系数Cp计算如下：

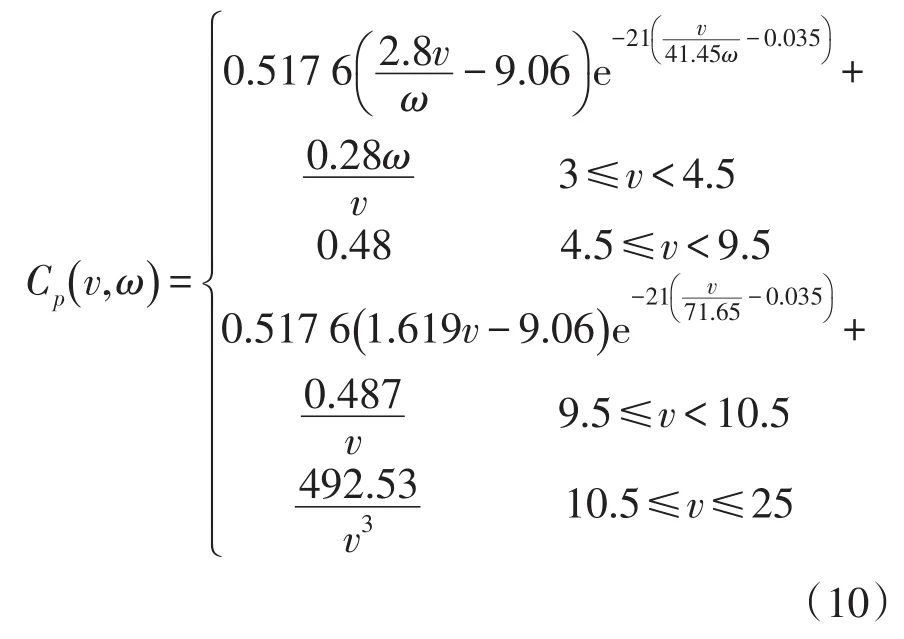
由式（10）可知，风能利用系数Cp的大小主要由风速决定，Cp与v的关系曲线如图2所示。

由式（2）和式（10）可得风电机组输出功率为

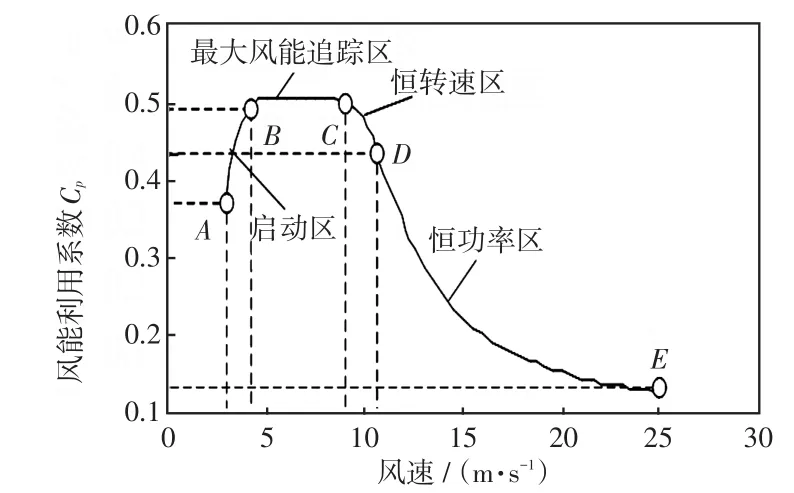
图2　风能利用系数曲线Fig.2　Curve ofCp

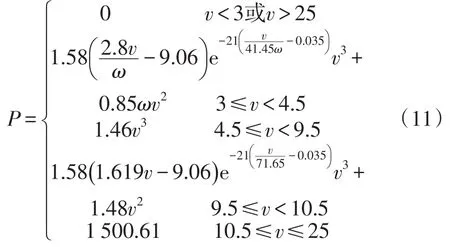
从而可得在标准空气密度 ρ=1.225 kg/m3下，该风电机组的标准风速-功率曲线如图3所示。

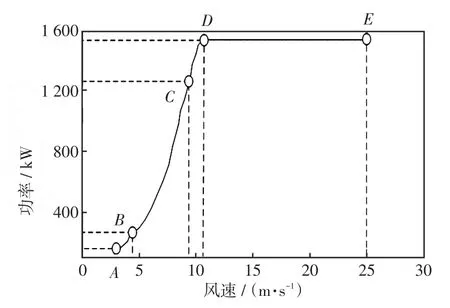
图3　SL1500/82型双馈感应风电机组标准风速-功率特性曲线Fig.3　Standard wind speed-power characteristic curve of SL1500/82 DFIG

从图3可看出，当风速低于切入风速3 m/s时，风中所蕴含的机械能不足以吹动风机叶片转动，风电机组输出功率为0；当风速达到风机切入风速3 m/s（即图3中A点）时，风电机组进入启动区，风机启动；当风速达到4.5 m/s（即图3中B点）时，风电机组并入电网，风电机组进入最大风能追踪区。风电机组转速在最高转速以下，风机桨距角处于不调节的定桨距运行状态，风电机组按最大功率追踪方式运行，其转速随风速做相应变化，以确保风机的风能利用系数始终保持最大值，因此随着风速的增加风电机组的输出功率逐渐增加；当风速达到9.5 m/s（即图3中C点）时，风轮转速达到最大值17 r/min，风电机组进入恒转速区。随着风速的增加，Cp逐渐减小（如图2），但是风电机组输出功率继续增加；当风速达到风机的额定风速10.5 m/s（即图3中D点）时，风电机组进入恒功率区。风电机组的输出功率达到额定值1 500 kW，随着风速的继续增加，通过控制风机的桨距角，使风电机组的输出功率维持在额定值；当风速达到风机切出风速25 m/s（即图3中的E点）时，风电机组离网，风机采取制动措施，风机停运，风电机组输出功率为0。

风电场由大量的风电机组组成，当输入风速大小相近时，各风电机组的输出功率特性一致，因此为简化起见，在建立风电场稳态模型时有必要对各风电机组进行分类处理。

2　风电机组分类方法

2.1最大树法

（2）标定。采用欧氏距离法建立各风电机组间的模糊相似矩阵R，计算式为

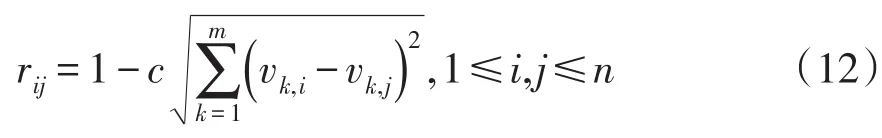
式中：n为风电机组台数；m为各风电机组运行时刻；vk,i、vk,j分别为第i和 j台风电机组在第k时刻的风速；rij为第i和 j台风电机组之间的相似系数；c为常数，使得rij∈（0,1）。

（3）画最大树。为便于实现计算机编程，采取如下步骤求取最大树：①对各台风电机组进行编号，以各台风电机组编号为顶点根据步骤（2）中所得模糊相似矩阵，在不产生圈的前提下选择相似度最大的顶点相互连接并标上相似系数，若形成最大树则结束程序；若形成若干子树，则继续以下步骤。②选择任一子树与其他子树各顶点之间的相似系数最大值连通两棵子树，直到构成最大树。

（4）选择阈值 μ∈［ ］0,1，裁剪掉最大树中相似系数rij＜μ的树枝，得到若干子树，它们的各个树枝均满足μ分类水平。μ选择较大时，所得分类多，分类结果准确性高，但是模型得不到有效简化；μ选择较小时，所得分类少，分类结果准确性差，但是模型得到有效简化。

2.2改进型最大树法

最大树法需要分别计算任意两台风电机组之间的相似系数，当风电场内含有多台风电机组时，此方法计算复杂、占用系统内存大、程序运行时间长，针对以上缺陷本文提出了一种改进型最大树法。改进型最大树法的实现步骤如下：

（1）分别建立以w1为起点的各条树枝，设定初始阈值μ，如图4所示。

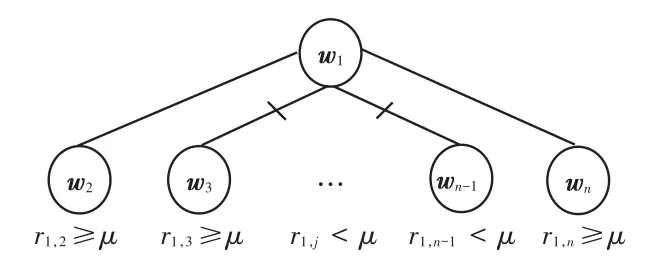
图4　一次迭代Fig.4　First iteration

裁剪掉相似系数低于阈值μ的树枝，得到一组与1号风电机组相似度较高的机群，从而完成一次迭代（设只有w2和wn与w1的相似系数满足不低于μ），得到一组分类结果，一次迭代结果如图5所示。

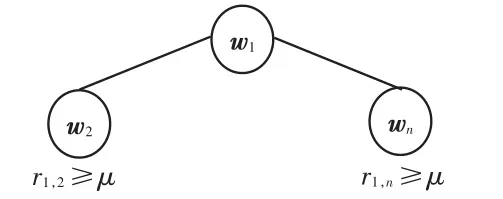
图5　一次迭代结果Fig.5　Result of the first iteration

（2）建立以w3为起点的各条树枝，裁剪掉相似系数低于μ的树枝，完成第二次迭代，如图6所示。

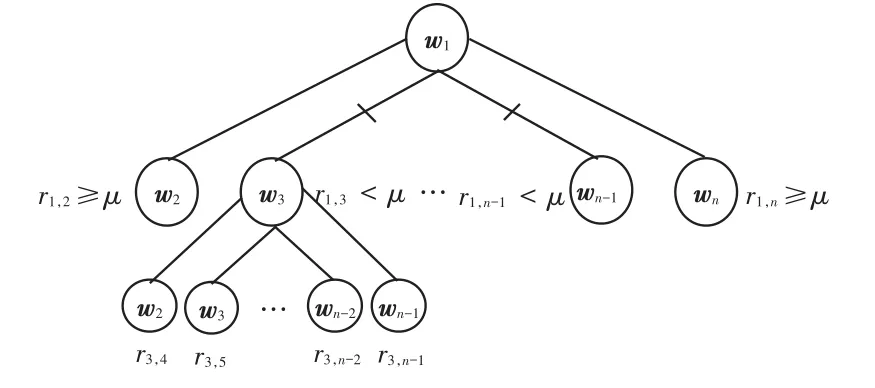
图6　二次迭代Fig.6　Second iteration

（3）以此类推，直到完成所有风电机组的分类。若分类结果m＞k（m为机群分类数目，k为所需机群分类数），修正 μ（μ=μ±Δμ），重复步骤（1）～（3），直到将风电场内所有风电机组分为k类。

改进型最大树法不需要全部计算任意两台风电机组之间的相似系数，并且能够准确地输出所需风电场机群分类结果，因此相比最大树法，其计算量、内存占用量以及程序运行时间都大大降低，并且能够按照所需分类数自动输出机群分类结果，大大简化了用户选择合适阈值μ的过程。

3　风电机组风速-功率特性曲线

对山西某实际风电场1号风电机组2013年1月16日—1月31日的实测数据进行处理，剔除异常及故障运行点，得到该风电机组的实际风速-功率散点图如图7所示。

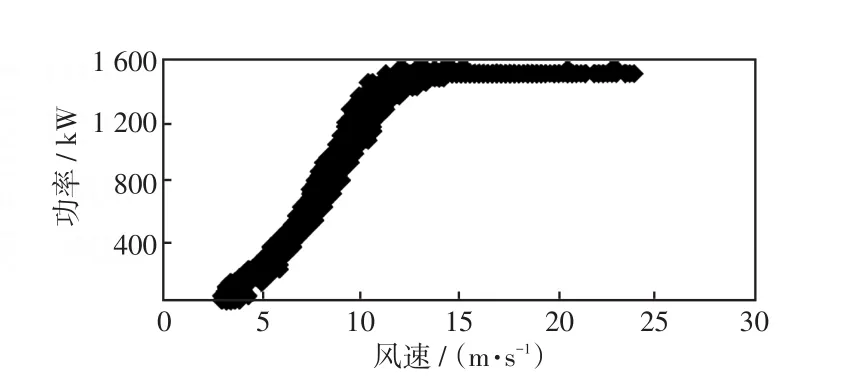
图7　1号风电机组实际运行特性Fig.7　ActualoperationcharacteristicofNo.1windturbine

从图7中看出，该风电场内风电机组并未完全按照图3所示曲线运行，而是运行在一个较宽的带状区域，因此不能采用标准风速-功率特性曲线来反映所有风电机组的实际运行特性。

风电机组的输出功率主要由其所受风速决定［15］，忽略风电机组内部特性，将其看作一个随风速变化的有功源。风电机组风速-功率函数关系为

按风速大小对风速-功率散点图进行分区处理，将风速由小到大划分为45个区段，各区段分别为vci+Δv,v2±Δv,…,v44±Δv,vco-Δv，其中vci和vco分别为风机切入和切出风速，首、末区段的宽度为Δv，其余各区段宽度为2Δv，计算各区段有功功率平均值为

式中：Ni为第i个区段内实测功率个数，i=1，2，…，45；Pi,j为第i个区段内第j个实测功率值。

第i个区段内风速-有功功率均值点为（vi,Pi,mean）。因此，对于整个风速区间计算得到45个风 速 -有 功 均 值 点（vci,P1,mean）,（v2,P2,mean）,…,（vco,P45,mean），从而得到能够反映该风电机组实际运行特性的风速-功率特性曲线。

4　仿真验证

4.1基于实测数据的风电场机群分类

算例所用风速数据为山西某风电场2013年1月16日—1月31日一期34台风电机组每10 min的运行数据。该风电场一期风电机组布置图如图8所示。

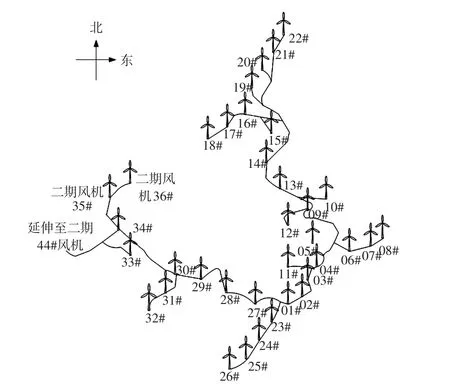
图8　风电场一期风电机组Fig.8　Arrangement of the first phase for an actual wind farm

从图8中可以看出，风电场内各台风电机组随机分布，它们所受风速由于所处地理位置的不同而有所差异，因此其运行特性也不完全一致。但是风电场内存在所受风速以及运行特性相似的风电机组，将这些机组划分到同一机群，该类机群的运行特性能近似反映这些风机的运行特性。

4.1.1基于最大树法的风电机组分类结果

（2）标定。采用欧氏距离法建立各风电机组之间的模糊相似矩阵R，其中c取1/200，计算结果如式（16）所示。

式中：R为对称矩阵，R1、R2和R3组成了R的下三角矩阵。

（3）画最大树。最大树如图9所示。

（4）选择不同的阈值μ时，机群分类结果如表2所示。

表2　机群分类结果Tab.2　Classification results of wind turbines

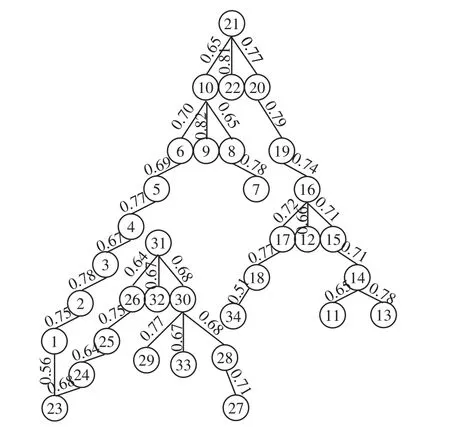
图9　最大树Fig.9　Maximum tree

从表2中可以看出，随着μ的增大风机机群分类数逐渐增加，分类结果更加准确。由文献［10］可知，机群分类数为3时已有较高的准确性，故为简化起见，本文选择阈值μ=0.64。对最大树进行裁剪，得到机群分类结果如图10所示。

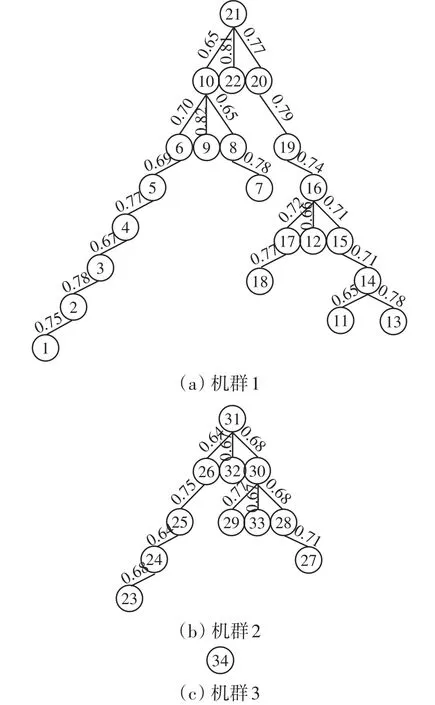
图10　最大树法机群分类结果Fig.10　Classification results of wind turbines by the method of maximum tree

4.1.2基于改进型最大树法的风电机组分类结果

μ的初始值选为0.8，Δμ为0.01。为了对比分析改进最大树法和最大树法的机群分类结果，机群分类数k取为3。经过17次迭代计算程序运行结束，输出3类机群，如图11所示。通过对比图10和图11可知，2种聚类方法分类结果相同，但是当机群分类结果均为3时，对于最大树法，需要计算1 156次权重系数；而对于改进型最大树法，只需要计算440次权重系数，因此改进型最大树法不仅能够减小程序的内存占用率，还可以提高程序运行速度。

4.2各类机群实测风速-功率特性曲线

分别计算4.1节中3类机群各风速下的平均功率，各风速取值为vci=3 m/s,v2=3.5 m/s,…,vco=25 m/s，Δv取值为0.05 m/s，分别计算3类机群的风速-有功功率均值点（vci,P1,mean）,（v2,P2,mean）,…,（vco,P45,mean），绘制风电机组标准风速-功率特性曲线和以上3类机群的实测风速-功率特性曲线，如图12所示。

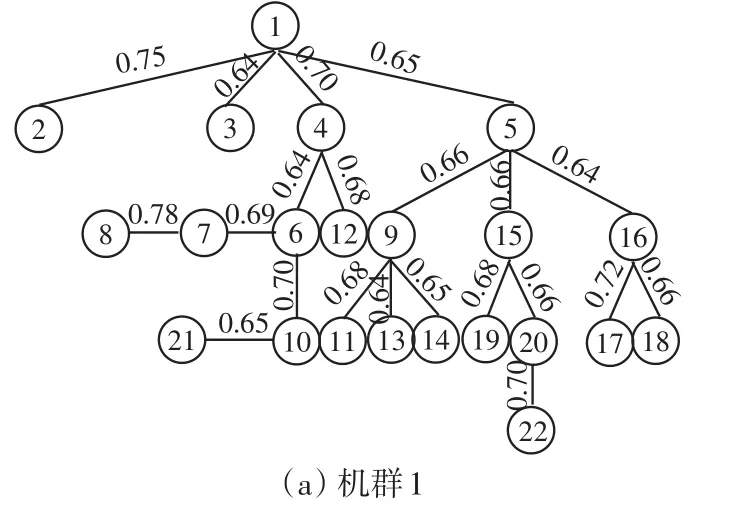
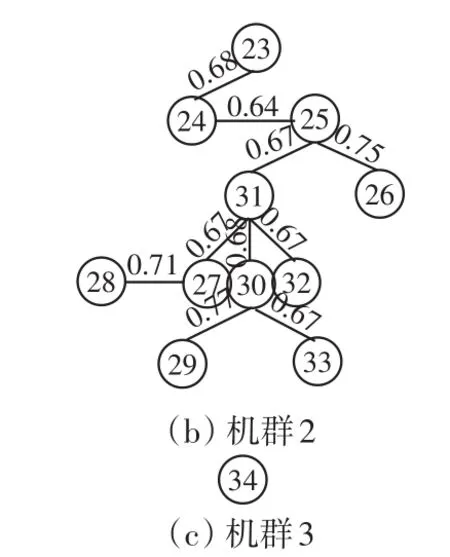
图11　改进型最大树法风电机组分类结果Fig.11　Classification results of wind turbines by the method of improved maximum tree

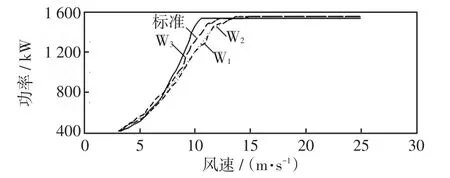
图12　3类机群的标准和实测风速-功率特性曲线对比Fig.12　Contrast between standard and actual wind speed-active power characteristic curves for the 3 classified wind turbines

3类机群实测风速-功率特性曲线与标准风速-功率特性曲线的标准差计算如式（17），结果如表3所示。

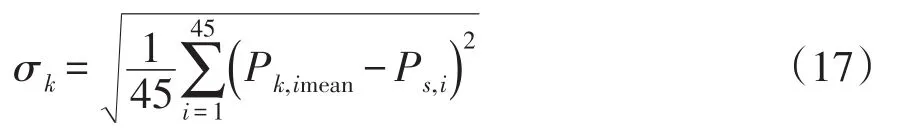
式中：k=1～3为机群分类数；Pk,imean为k类机群在第i个区段的输出功率平均值；Ps,i为各区段风速中心vi对应的标准输出功率。

表3　机群功率特性标准差Tab.3　Standard deviation of wind turbine power curves

由图8、图12和表3知：机群3仅含34#风电机组，该风机受其他风机尾流影响较小，故其运行特性更接近标准功率特性曲线；机群1和2含风电机组数目多，各风机间尾流影响较大，故其运行特性更偏离标准功特曲线，因此有必要在建模时考虑机群间运行特性的差异。由图2和式（11）知，风电机组运行于4个不同区域，分别建立图12中标准、机群W1、W2和W3风速-功率特性曲线分段函数关系为

由式（18）～（21）可知，3类机群的实测风速-功率分段函数关系不同于在标准条件下风电机组的风速-功率分段函数关系，更能反映出各台风电机组的实际运行特性。

4.3风电场稳态模型

计算风电场和各机群的等值风速，由式（18）～（21）分别建立传统（式（22））和三机等效（式（23））风电场稳态模型。

式中：Ptr为传统风电场稳态模型输出功率；nw为风电场内机组数目；vˉ为风电场内所有风电机组平均风速。

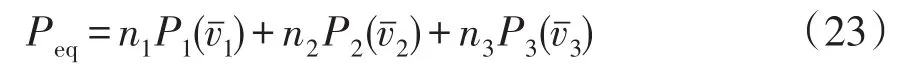
式中：Peq为三机等效风电场稳态模型输出功率；n1、n2和n3分别为机群W1、W2和W3中所含风电机组台数；分别为机群W1、W2和W3中所含风电机组的平均风速。

以风电场一期34台风电机组2013年1月21日实际运行数据为例，分别绘制风电场实际输出功率曲线、传统和三机等效风电场稳态模型输出功率曲线，如图13所示。

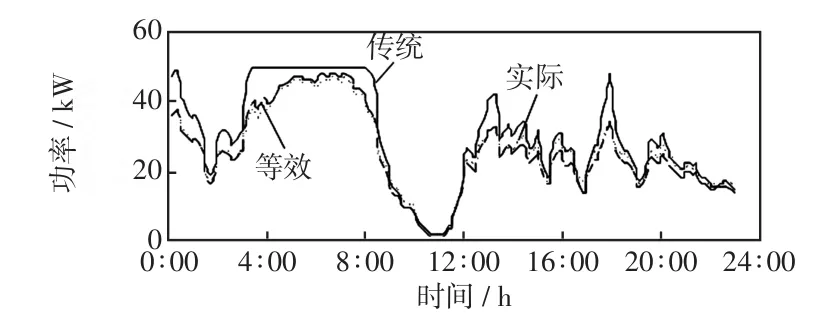
图13　传统、三机等效风电场稳态模型和风电场实际输出功率曲线Fig.13　Wind power curves of the traditional，three-machine equivalent model and actual wind power output

分别计算传统风电场稳态模型与三机等效风电场稳态模型输出功率与实际风电场输出功率的绝对百分比误差APE（absolute percentage error）和平均绝对百分比误差MAPE（mean absolute percentage error），计算公式分别如式（24）和（25），计算结果如图14所示。

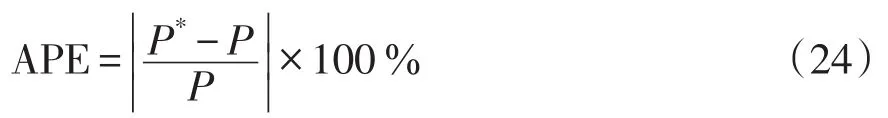
式中：P*为风电场稳态模型输出功率；P为风电场实际输出功率。

式中，T为所取风电场运行时刻数。

图14　传统、三机等效风电场稳态模型绝对百分比误差曲线Fig.14　APE curves of the traditional and three-machine equivalent model of wind farm

从图13和14中可以看出，本文所提三机等效风电场稳态模型相比传统风电场稳态模型具有较高的精度，并且能够较好地反映风电场实际输出功率的变化。计算得到传统风电场稳态模型和三机等效风电场稳态模型的MAPE分别为14.31%和5.83%，APE的最大值分别为40.01%和22.41%。

通过以上分析可知，本文所提基于实测数据的三机等效风电场稳态模型能够更准确地反映风电场的实际运行情况，具有广泛的实用价值。

5　结论

本文分析了双馈风电机组的4个不同运行区域，并推导出它在各运行区域下的运行特性得到如下结论：

（1）风电场内各台风电机组运行于一个较宽的风速-功率带状区域，风机生产厂家提供的标准风速-功率特性曲线难以准确地反映其实际运行的特性。

（2）改进型最大树法能够准确地对风电场内风电机组进行机群分类，同最大树法相比，降低了程序内存占用率，提高了程序运行速度。

（3）三机等效风电场稳态模型有效地提高了传统风电场稳态模型的精度，能够更准确地反映风电场的实际运行特性。

［1］蒋程，刘文霞，于雷，等（Jiang Cheng，Liu Wenxia，Yu Lei，et al）.计及风电的发电系统可靠性评估（Reliability assessment of power generation system considering wind power penetration）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（4）：7-13.

［2］白鸿斌，王瑞红（Bai Hongbin，Wang Ruihong）.风电场并网对电网电能质量的影响分析（Influence of the gridconnected wind farm on power quality）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（1）：120-124.

［3］唐民，童小娇，文强（Tang Min，Tong Xiaojiao，Wen Qiang）.计及网络参数不确定的含风电场安全经济调度（Security economic dispatch of power system integrated with wind farms considering uncertainty of network parameters）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（2）：27-34.

［4］李光允，陈小虎，唐国庆（Li Guangyun，Chen Xiaohu，Tang Guoqing）.大型风力发电场等值建模研究综述（Review on equivalent modeling for large-scale wind power field）［J］.华北电力大学学报（Journal of North China Electric Power University），2006，33（1）：42-46.

［5］孙建锋，焦连伟，吴俊玲，等（Sun Jianfeng，Jiao Lianwei，Wu Junling，et al）.风电场发电机动态等值问题的研究（Research on multi-machine dynamic aggregation in wind farm）［J］.电网技术（Power System Technology），2004，28（7）：58-61.

［6］曹娜，赵海翔，陈默子，等（Cao Na，Zhao Haixiang，Chen Mozi，et al）.潮流计算中风电场的等值（Equivalence method of wind farm in steady-state load flow calculation）［J］.电网技术（Power System Technology），2006，30（9）：53-56.

［7］严干贵，李鸿博，穆钢，等（Yan Gangui，Li Hongbo，Mu Gang，et al）.基于等效风速的风电场等值建模（Equivalent model of wind farm by using the equivalent wind speed）［J］.东北电力大学学报（Journal of Northeast Dianli University），2011，31（3）：13-19.

［8］卢锦玲，石少通，卢洋（Lu Jinling，Shi Shaotong，Lu Yang）.含大规模风电场的电网静态电压稳定性评估（Static voltage stability assessment on the grid with largescale wind farm connection）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（6）：73-80.

［9］余洋，刘永光，董胜元（Yu Yang，Liu Yongguang，Dong Shengyuan）.基于运行数据的风电场等效建模方法比较（Comparative study on wind farm equivalent modeling based on operation data）［J］.电网与清洁能源（Power Systems and Clean Energy），2009，25（12）：79-83.

［10］苏勋文，米增强，陈盈今，等（Su Xunwen，Mi Zengqiang，Chen Yingjin，et al）.基于运行数据的风电机组建模方法（Method for modeling wind turbines based on operating data）［J］.电力系统保护与控制（Power System Protection and Control），2010，38（9）：50-54，71.

［11］王钤，潘险险，陈迎，等（Wang Qian，Pan Xianxian，Chen Ying，et al）.基于实测数据的风电场风速-功率模型的研究（Study of wind speed-active power model for wind farm based on measured data）［J］.电力系统保护与控制（Power System Protection and Control），2014，42（2）：23-27.

［12］郎斌斌，穆钢，严干贵，等（Lang Binbin，Mu Gang，Yan Gangui，et al）.联网风电机组风速-功率特性曲线的研究（Research on wind speed vs output power characteristic curve of wind power generator interconnected with power grid）［J］.电网技术（Power System Technology），2008，32（12）：70-74.

［13］Heier Siegiried.Grid Integration of Wind Energy Conversion Systems［M］.New York：John Wiley&Sons Ltd，1998.

［14］李培强，李欣然，陈凤，等（Li Peiqiang，Li Xinran，Chen Feng，et al）.模糊聚类在统计综合法负荷建模中的应用（Application of fuzzy clustering in component-based modeling approach）［J］.电力自动化设备（Electric Power Automation Equipment），2003，23（5）：43-45，74.

［15］田春筝，李琼林，宋晓凯（Tian Chunzheng，Li Qionglin，Song Xiaokai）.风电场建模及其对接入电网稳定性的影响分析（Modeling and analysis of the stability for the power system considering the integration of the wind farms）［J］.电力系统保护与控制（Power System Protection and Control），2009，37（19）：46-51.

Steady-state Model of Wind Farm Considering Operation Data

WANG Haiming1，HAN Xiaoqing1，TIAN Jianyan1，QIN Wenping1，LIU Zhijuan1，MI Xiaodong2
（1.Taiyuan University of Technology，Taiyuan 030024，China；2.Xinzhou Power Supply Company，Xinzhou 034000，China）

To establish the steady-state model of a wind farm accurately，a three-machine equivalent steady model is proposed based on the measured data after analyzing the steady-state characteristics of wind turbines in different operation regions.First，this paper analyzes the steady active power characteristics of wind turbines in 4 operation regions.By means of improved maximum tree method，the wind turbines are divided into 3 groups according to the measured wind speed data.Then，the wind speed-active power curve and piecewise function are obtained for each group of turbines based on the 4 operation regions.Finally，a three-machine equivalent steady-state model of a wind farm is established by calculating the equivalent wind speed of the three groups.Simulation results show that the proposed method can effectively improve the accuracy of the steady-state model of a wind farm.

measured data；three-machine；steady-state model；improved maximum tree method；wind speed-active power curve

TM461

A

1003-8930（2016）09-0027-09

10.3969/j.issn.1003-8930.2016.09.005

王海明（1988—），男，硕士研究生，研究方向为风电场建模、风电场并网电能质量分析。Email：wanghaiming61@163.com

韩肖清（1964—），女，博士，教授，博士生导师，研究方向为电力系统运行与控制、新能源发电。Email：hanxiaoqing@tyut.edu.cn

田建艳（1966—），女，博士，教授，研究方向为复杂工业过程的建模与控制及灰色系统理论。Email：tut_tianjy@163.com

2014-09-25；

2015-11-30

国家自然科学基金资助项目（51277127）；山西省科技攻关项目（20130321027-1）；山西省高等学校中青年拔尖创新人才支持计划资助项目