基于LMD和TEO的电能质量扰动检测分析

周　超，黄　纯

（湖南大学电气与信息工程学院，长沙 410082）

基于LMD和TEO的电能质量扰动检测分析

周超，黄纯

（湖南大学电气与信息工程学院，长沙 410082）

分析了局部均值分解LMD（local mean decomposition）在扰动检测中时间定位不足的原因，提出了基于LMD和Teager能量算子TEO（Tteager energy operator）的电能质量扰动信号检测分析方法。该方法由LMD和Teager能量算子2部分组成。首先利用LMD将电压信号分解成若干个乘积函数PF（product function），再用Teager能量算子解调PF分量得到信号的瞬时幅值包络和瞬时频率。根据时频图频率突变点，可以有效地检测扰动发生的起止时刻。与LMD相比，所提出的方法具有频率、幅值检测准确，定位能力强，端部失真小等优点，能有效检测分析非平稳电能质量扰动信号。

局部均值分解；乘积函数；Teager能量算子；电能质量；信号处理

近年来，电力电子元件的大量使用及非线性负载的增多，给电网造成严重污染，电网中存在的谐波、间谐波，电压暂升、暂降、短时中断以及电压闪变等电能质量问题备受关注［1-5］。因此，必需对电能质量扰动进行准确和快速的检测分析。

在电能质量扰动检测分析方法中，小波变换分析非平稳、非线性信号时，缺乏自适应性，对噪声敏感，受小波基函数选择的限制等［6-7］；短时网格分形数检测分析电能质量扰动，可以确定扰动发生的起止时刻，但该原理无法确定暂态振荡的终止时刻［8］；数学形态学方法在信号过零点突变等情况下仍然具有良好的检测效果，但最大的缺点在于结构元素的选取依据不足［9］；希尔伯特-黄HHT（Hilbert-Huang transform）算法自适应性好，在电能质量扰动检测方面取得了较好的效果，但HHT采用三次样条函数插值会出现过、欠包络现象，还有端点效应等问题［10］；Prony算法在处理非平稳信号时，不能提供信号的频率瞬变特性和局部特征的时变特性［11］。

LMD［12］（local mean decomposition）是一种自适应时频分析方法，可以将信号分解成若干个乘积函数之和，每个PF（product function）分量由纯调频FM（frequency modulated）函数和调幅AM（amplitude modulated）函数之积构成。PF分量的幅值即为包络信号，PF分量的频率可由纯调频函数的反函数求导获得，该方法称为“直接法”。文献［13］将LMD“直接法”用于电能质量谐波及其间谐波的分析，但定位效果不理想。文献［14］提出了基于LMD的Hilbert变换在电能质量扰动中的应用，并取得了较好的效果。

电能质量扰动信号可看做多分量调制信号，其解调方法有Hilbert变换解调、Teager能量算子［15］TEO（Teager energy operator）解调等，TEO是一种非线性算子，能够跟踪信号的瞬时能量，准确检测到突变值。在机械故障诊断中，被用来提取振动信号中的故障信息，处理结果优于Hilbert解调。但TEO解调方法求取信号瞬时幅值包络只适用于单分量信号，对于多分量信号则可由LMD或经验模态分解EMD（empirical mode decomposition）算法提取有用的单分量进行分析，文献［16］采用EMD及其能量算子解调方法在机械故障诊断应用中取得了较好的效果。本文提出了采用LMD及TEO检测分析电能质量扰动的方法。

1　LMD和TEO原理

1.1LMD

LMD本质上是根据信号的包络特征自适应地将一个非平稳、非线性信号按频率递减的规律逐级分解，得到若干个具有一定物理意义的PF分量，每一个PF分量由纯调频函数和纯包络函数之积构成。若信号为x（t），其分解步骤［12-13］如下。

1）找出信号x（t）的局部极值点ni，计算相邻两个极值点ni、ni+1平均值记为mi，则有：

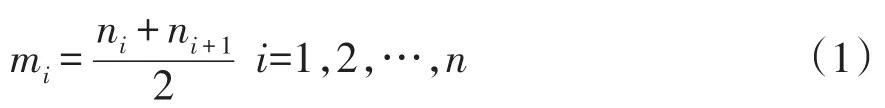
将式（1）中所有相邻的局部均值点mi和mi+1用折线连接起来，然后用滑动平均法对其进行平滑处理，得到局部均值函数m11（t）。

2）计算包络估计值ai

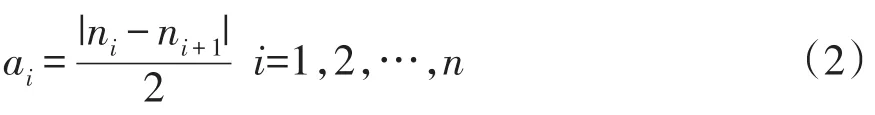
将式（2）中所有相邻的局部均值点a1和ai+1用折线连接起来，然后用滑动平均法对其进行平滑处理，得到包络估计函数a11（t）。

3）将局部均值函数m11（t）从原始信号x（t）中分离出来，得到h11（t）：

4）用h11（t）除以包络估计函数a11（t），得到调频信号为

对s11（t）重复上述步骤，得到s11（t）的包络估计函数a12（t）。如果a12（t）不等于1，则信号s11（t）不是一个纯调频信号，需要重复上述迭代过程n次，直至s1n（t）为一个纯调频信号，即s1n（t）的包络估计函数a1（n+1）（t）=1有：

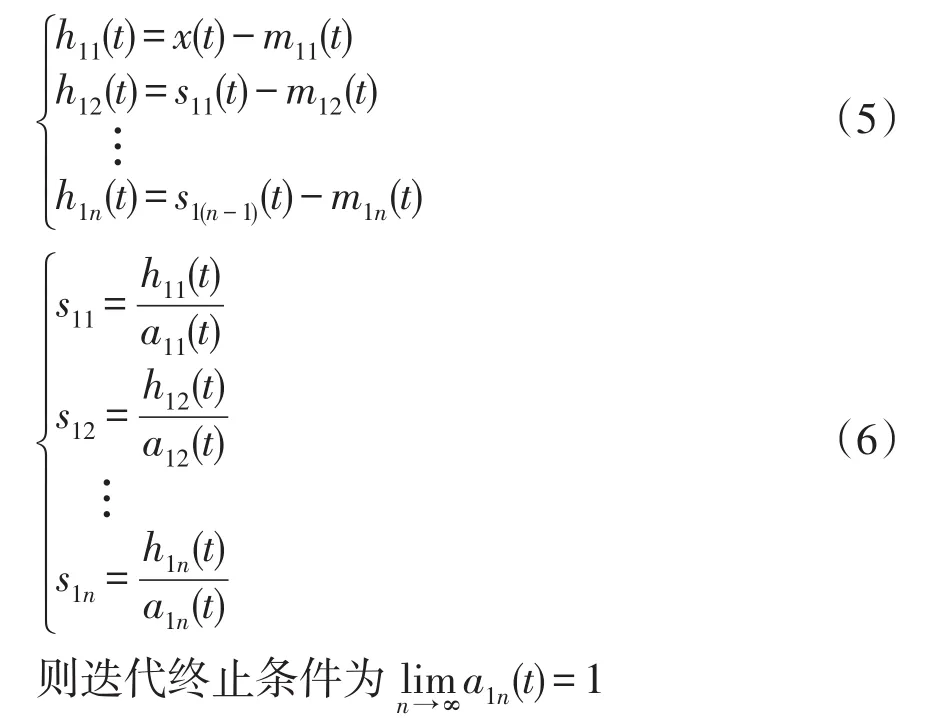
实际应用中，为避免过多分解次数，设一个变动量Δe，当1-Δe≤a1n（t）≤1+Δe时，迭代终止。

5）将迭代过程中产生的所有包络估计函数做乘积，得到包络信号a1（t）为

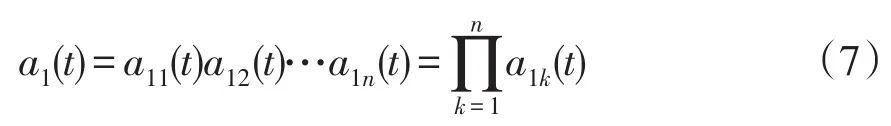
6）将式（7）得到的包络信号a1（t）与纯调频信号s1n（t）做乘积，得到原始信号x（t）的第一个PF分量，则有：

PF1包含了原始信号中的最高频率成分，是一个单分量的调幅-调频信号，其瞬时频率为

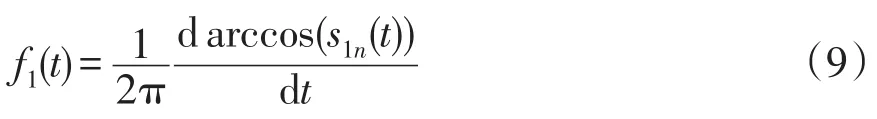
7）将PF1（t）分量从原始信号x（t）中分离出来，得信号u1（t），将u1（t）作为新的数据重复以上步骤，循环k次，直到uk（t）为单调函数为止。

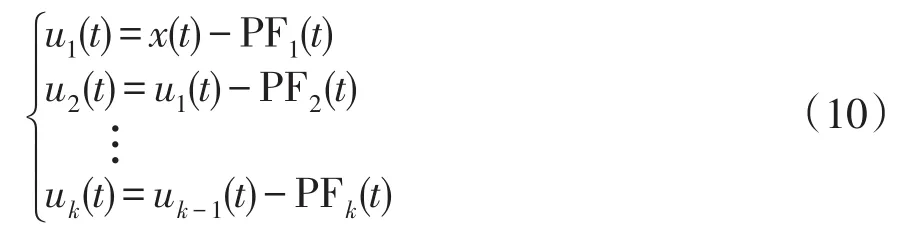
从以上步骤可以看出，原始信号可由uk（t）和所有PF分量重构，即：

可以看出每个PF分量由一个纯包络函数和纯调频函数相乘构成，但纯调频函数为余弦函数，求瞬时频率时要求值在±1之间。若某时刻信号发生扰动时，纯调频函数值会突变而不在有效值之内，如果将该处极值点置为±1，扰动起止点处的频率就没有明显突变，无法准确进行时间定位。Teager能量算子只使用了信号的3个采样值点，能够迅速准确跟踪信号的幅值和频率，具有快速响应的能力，突变信息可完全被保留，因此定位准确。LMD分解得到的PF分量通过TEO解调，可得到原信号的幅频信息，避免了“直接法”求取频率时条件的限制。

1.2TEO

若信号的离散形式为

选取相邻的3个采样点构成方程组如下：

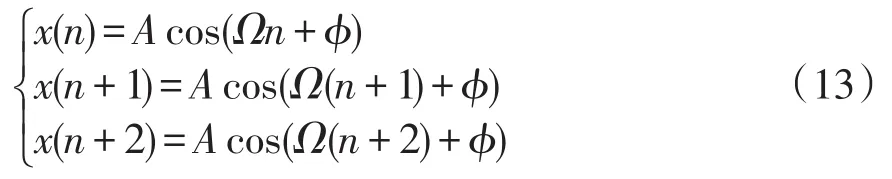
解此方程组可得：

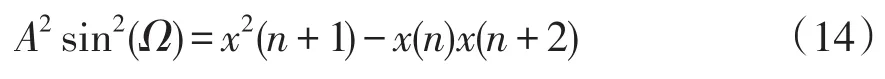
当Ω足够小时，sin（Ω）=Ω，当把Ω限制在Ω＜0.784 5（即）时，sin（Ω）与Ω两者的相对误差小于11%），此时式（14）可表示为

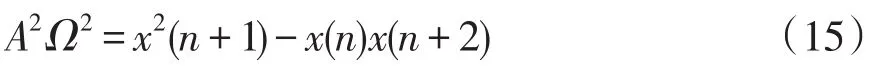
即为Teager能量算子。

定义信号x（t）的TEO为

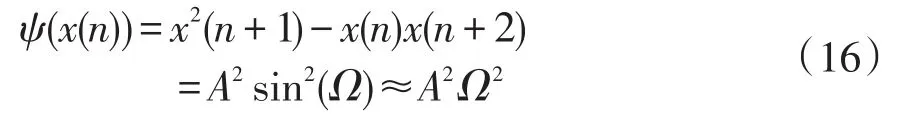
1）对于幅值和频率不变的信号，可表示为

选择信号x（n）连续的两个采样点构成对称差分信号为

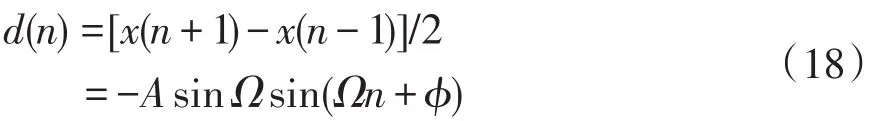
则得到d（n）的TEO为

根据式（17）和式（18）可知

因此，信号x（n）的频率、幅值可表示为

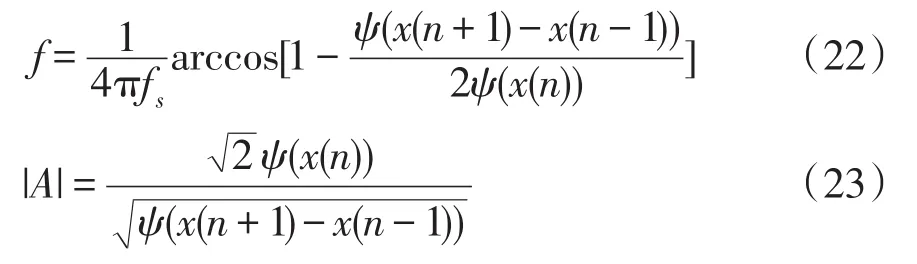
2）对于频率和幅度均时变的信号，可表示为

则可以构成对称差分信号为

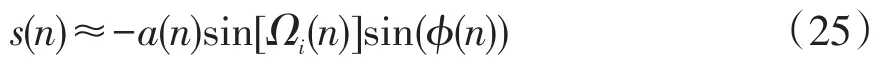
则得到s（n）的TEO为

因此，时变信号x（n）的频率、幅值可表示为

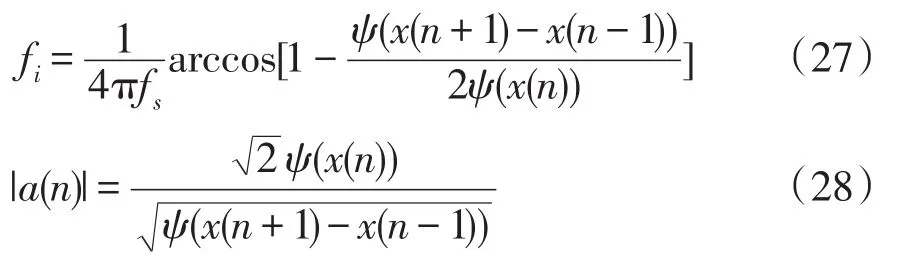
该文利用LMD和Teager能量算子（LMD-TEO）对几种常见电能质量扰动信号（谐波失真信号，电压暂降、暂升加噪声、短时中断信号，电压闪变信号）进行分解、解调和时域分析，从而定位扰动起止时刻，与LMD方法进行仿真比较，进一步验证了LMD-TEO方法的可行性和实用性，其检测分析流程如图1所示。

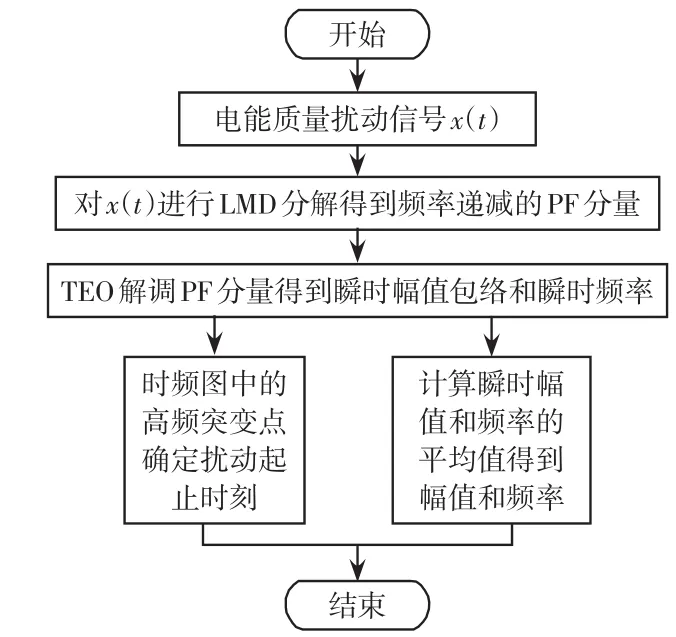
图1　电能质量扰动信号检测分析流程示意Fig.1　Flow chart of power quality disturbance detection and analysis

2　基于LMD-TEO的电能质量扰动信号检测分析

2.1谐波失真信号分析

2.1.1时变谐波信号

设时变谐波信号数学模型为

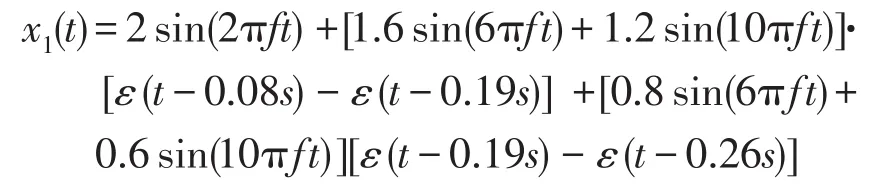
其中0s≤t≤0.26 s，ε（t）为阶跃信号，f=50 Hz，采样频率为6 400 Hz，仿真结果如图2所示。

运用LMD分解时变谐波信号得到按频率依次递减的PF1、PF2、PF3分量，如图2（b）-（d）所示。用TEO解调PF1、PF2分量，得到瞬时幅值包络和频率曲线，如图2（e）、（g）所示，由时频图（f）、（h）可知在扰动起止时刻出现了高频突变。根据突变点确定扰动发生和结束时刻为0.080 2 s和0.189 8 s。相对LMD，LMD-TEO定位能力有很大的提高，可和文献［17］采用的HHT方法相媲美。

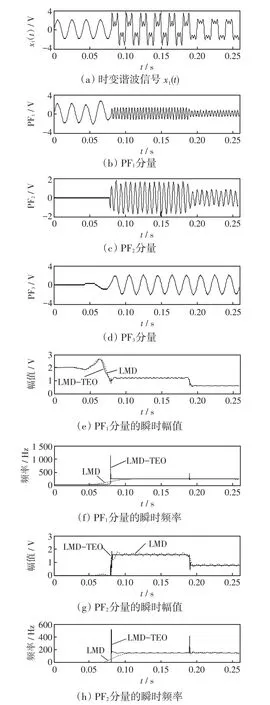
图2　时变谐波信号分析Fig.2　Time-frequency analysis of time-varying harmonic signals

在整个扰动时段内，可认为PF1分量为5次谐波信号，PF2分量为3次谐波信号，只是幅值发生了改变，频率保持不变。对各PF分量按式（22）、（23）分别求取瞬时频率和幅值，再计算谐波频率和幅值平均值得到5次谐波频率为249.8 Hz、3次谐波频率为150.3 Hz，在时间段0.080 2 s～0.189 8 s内，5次谐波、3次谐波信号幅值分别为1.198 V、1.590 V；在时间段0.189 8 s～0.26 s内，5次谐波、3次谐波信号幅值分别为0.602 V、0.800 V，相对误差很小。

2.1.2短时谐波失真信号

短时谐波信号如图3，设其数学模型为

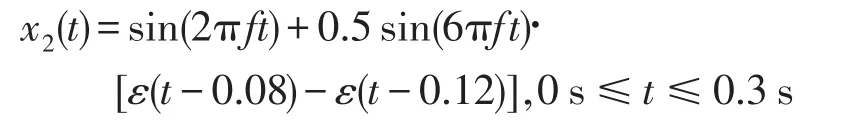
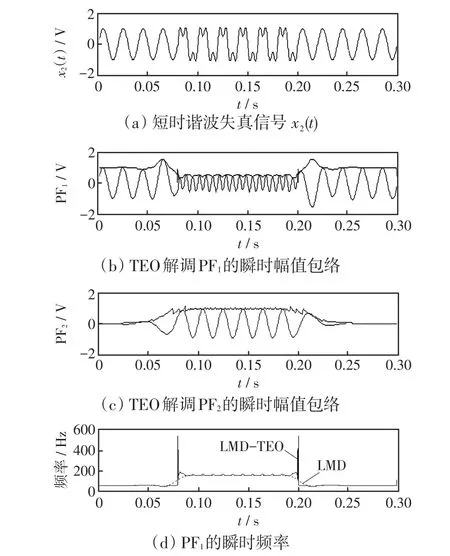
图3　短时谐波失真信号分析结果Fig.3　Analysis results of short-time harmonic signals

2.2电压暂降、暂升加噪声、短时中断信号分析

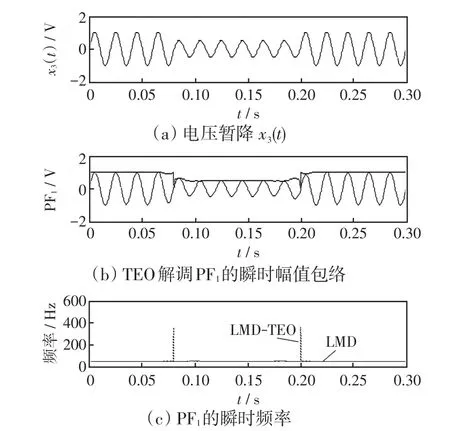
图4　电压暂降分析结果Fig.4　Analysis results of voltage sag

电压暂降信号x3（t）如图4，基波信号的幅值为1 V，扰动幅度0.5 V（0.08 s≤t≤0.2 s）。

用LMD分解x3（t）得到PF1分量，TEO解调PF1得幅值包络和瞬时频率如图4（b）、（c）所示，从时频图可以得到扰动起止时刻，从时幅图可知扰动信号的幅值。

用此方法也可以检测分析电压暂升加噪声、电压短时中断信号的时频特征及瞬时幅值信息，如图5和图6所示。

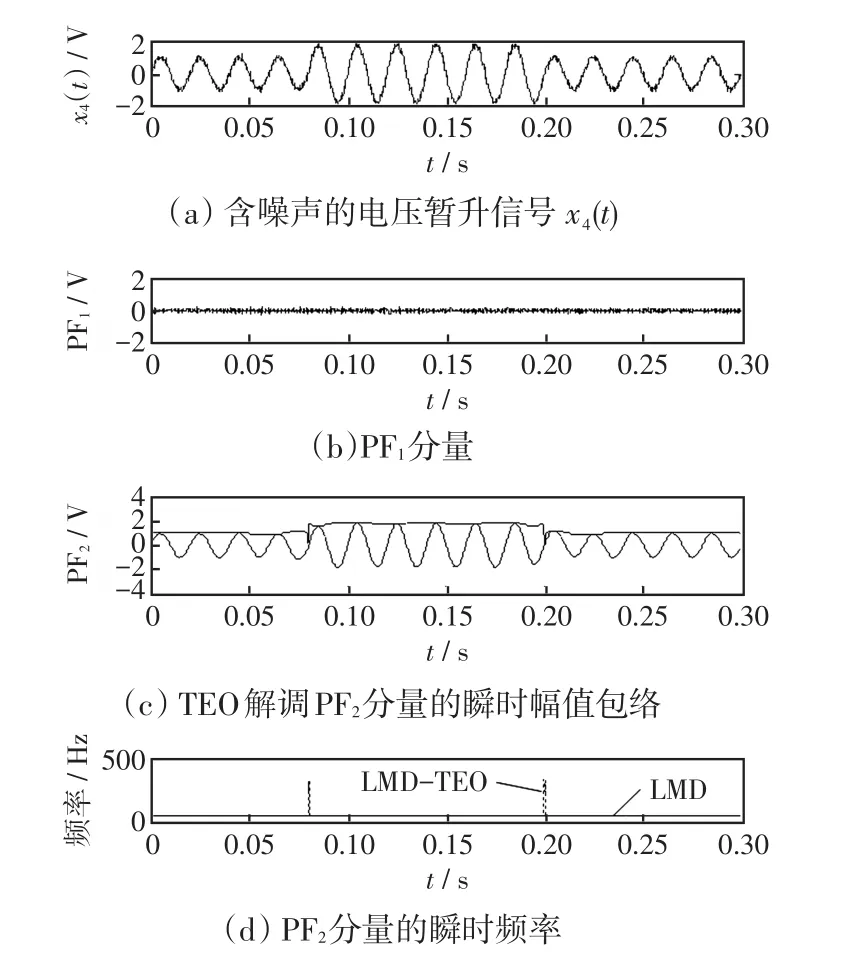
图5　电压暂升加噪声分析结果Fig.5　Analysis results of voltage rise mixed with noise

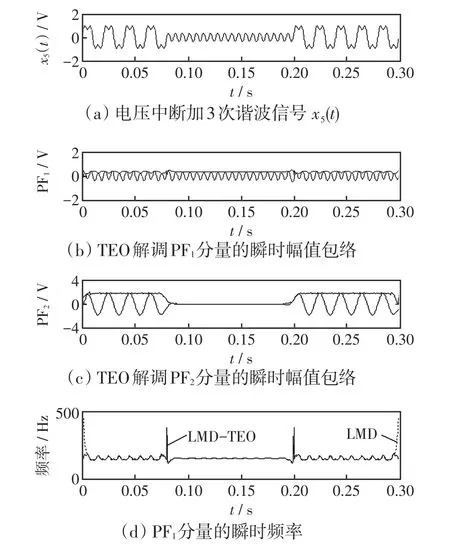
图6　电压短时中断时加入3次谐波分析结果Fig.6　Analysis result of voltage short interruptions joined by 3rd harmonic

发生电压短时中断后，由于扰动段内曲线没有极值点，不能检测出扰动发生的时刻。此时可在电压信号中加入幅值很小的谐波，例如3次谐波，进行LMD分解，此时可以看做是电压暂降混有谐波的情况。如图6（b）、（c）可知PF1为3次谐波分量，PF2为电压短时中断信号。如图6（d）时频图可定位电压短时中断扰动时间为0.079 8 s～0.201 0 s，突变频率为379.76 Hz和379.76 Hz，因此，加入幅值很小的高频谐波可以进行电压短时中断起止时间的检测。

图4～6结果表明：这3类扰动信号幅值发生了暂降或暂升，频率不变，除扰动发生和结束时刻有高频突变外，其他各段频率都是恒定的，且都为基波频率50 Hz。

2.3电压闪变信号分析

设电压闪变信号为

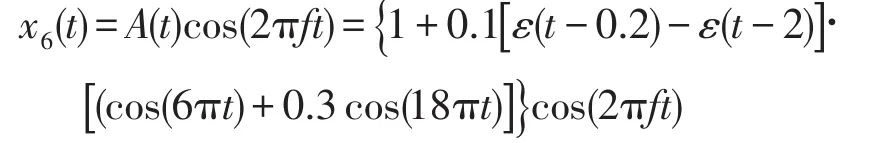
其中，0 s≤t≤3 s。

电压闪变包络信号A（t）包含着电压闪变的频率和幅值信息，LMD-TEO算法分解电压闪变信号获取基波幅值包络和基波频率如图7（b）、（c）。分析图7（c）中时频曲线的突变点可以定位闪变起止时刻。再对包络信号A（t）进行LMD-TEO分析得到包络信号PF分量的幅值和频率如图7（d）-（g）。可知检测多频信号时LMD-TEO比LMD精度高、端点效应小。

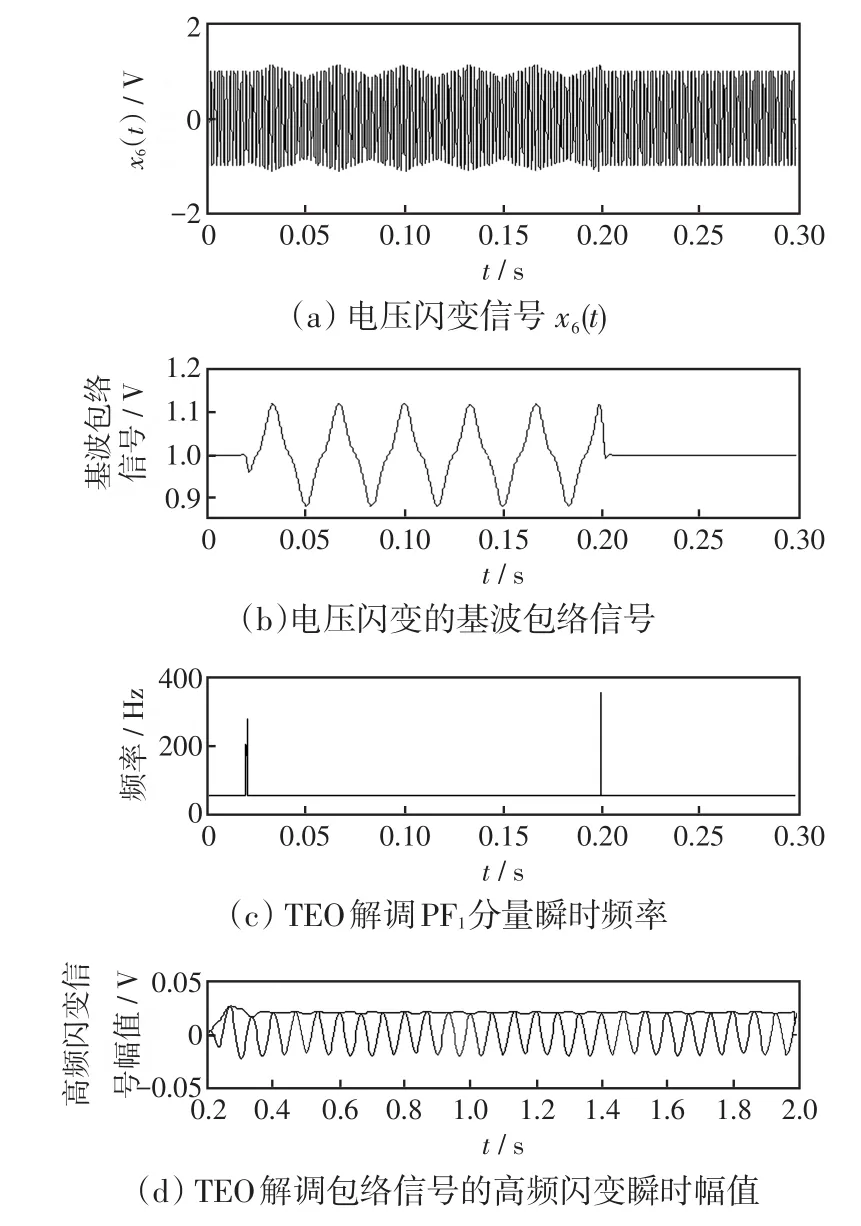
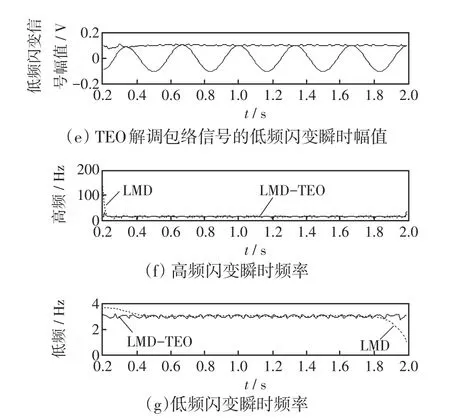
图7　电压闪变分析结果Fig.7　Analysis result of voltage flicker

仿真结果发现直接用TEO解调电压闪变信号包络，如含有高频谐波，振荡暂态等，容易发生失真，通过LMD分解出信号的高频部分，起到了滤波的作用。实际电力系统中，电压闪变波动值不会超过载波电压幅值的10%，调幅频率一般在0.05～35 Hz，对于低频范围TEO解调相对误差百分数不超过3%，因此，LMD-TEO方法分析电能质量扰动信号是可行的、有效的。

3　结论

（1）将LMD与TEO相结合对电能质量扰动信号进行分析，LMD分解得到的PF分量包含了信号的局部特征信息，运用TEO对PF分量解调得到瞬时频率和幅值包络曲线，可定位扰动发生的起止时间，提高了扰动起止时间的检测精度。

（2）LMD-TEO方法检测电能质量扰动信号瞬时幅值包络和瞬时频率，具有精度高、波动小等优点。

（3）在信号中加入高频谐波增加极值点，可以检测电压短时中断的起止时刻。

［1］Angrisani L，Daponte P，D'Apuzzo M.A measurement method based on wavelet transform for power quality analysis［J］.IEEE Trans on Power Delivery，1998，13（4）：990-998.

［2］肖湘宁.电能质量分析与控制［M］.北京：中国电力出版社，2004.

［3］仇新艳，李付亮（Qiu Xinyan，Li Fuliang）.基于ITD和K均值聚类的电能质量扰动分析与识别（Analysis and identification for power quality disturbance signals based on ITD and K-mean clustering algorithm）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（8）：54-59.

［4］张秀娟，徐永海，肖湘宁（Zhang Xiujuan，Xu Yonghai，Xiao Xiangning）.电能质量扰动小波变换检测与识别方法的发展（Development of wavelet-transform-based power quality disturbance detection and identification）［J］.电力自动化设备（Electric Power Automation Equipment），2003，23（9）：67-71.

［5］林海雪（Lin Haixue）.现代电能质量的基本问题（Main problem of modern power quality）［J］.电网技术（Power System Technology），2001，25（10）：5-12.

［6］胡铭，陈珩（Hu Ming，Chen Heng）.基于小波变换模极大值的电能质量扰动检测与定位（Detection and location of power quality disturbances using wavelet transform modulus maxima）［J］.电网技术（Power System Technology），2001，25（3）：12-16.

［7］杨桦，任震，唐卓尧（Yang Hua，Ren Zhen，Tang Zhuoyao）.基于小波变换检测谐波的新方法（A new method for harmonics detection based on wavelets transform）［J］.电力系统自动化（Automation of Electric Power Systems），1997，21（10）：39-42.

［8］赵瑞娜，齐泽锋，陈允平，等（Zhao Ruina，Qi Zefeng，Chen Yunping，et al）.基于短时网格分形维数的电能质量扰动检测（Detection of power quality disturbances based on short-duration grille fractal dimension）［J］.继电器（Relay），2001，29（11）：21-23.

［9］凌玲，徐政（Ling Ling，Xu Zheng）.基于数学形态学的动态电能质量扰动的检测与分类方法（Mathematical morphology based detection and classification of dynamic power quality disturbances）［J］.电网技术（Power System Technology），2006，30（5）：62-66.

［10］刘志刚，李文帆，孙婉璐（Liu Zhigang，Li Wenfan，Sun Wanlu）.Hilbert-Huang变换及其在电力系统中的应用（Hilbert-Huang transform and its applications in power system）［J］.电力自动化设备（Electric Power Automation Equipment），2012，32（4）：109-116.

［11］王铁强，贺仁睦，徐东杰，等（Wang Tieqiang，He Renmu，Xu Dongjie，et al）.Prony算法分析低频振荡的有效性研究（The validate study of Prony analysis for low frequency oscillation in power system）［J］.中国电力（Electric Power），2001，34（11）：38-41.

［12］Smith J S.The local mean decomposition and its application to EEG perception data［J］.Journal of the Royal Society Interface，2005，2（5）：443-454.

［13］黄传金，曹文思，陈铁军，等（Huang Chuanjin，Cao Wensi，Chen Tiejun，et al）.局部均值分解在电力系统间谐波和谐波失真信号检测中的应用（Application of local mean decomposition in power quality disturbance detection）［J］.电力系统自动化设备（Electric Power Auto-mation Equipment），2013，33（9）：68-73，81.

［14］宋海军，黄传金，刘宏超，等（Song Haijun，Huang Chuanjin，Liu Hongchao，et al）.基于改进LMD的电能质量扰动检测新方法（A new power quality disturbance detection based on improved LMD）［J］.中国电机工程学报（Proceedings of the CSEE），2014，34（10）：1700-1708.

［15］Maragos P，Kaiser J F，Quatieri T F.Energy separation in signal modulations with applications to speech analysis［J］.IEEE Trans on Signal Processing，1993，41（10）：3024-3051.

［16］程军圣，于德介，杨宇（Cheng Junsheng，Yu Dejie，Yang Yu）.基于EMD的能量算子解调方法及其在机械故障诊断中的应用（Energy operator demodulating approach based on EMD and its application in mechanical fault diagnosis）［J］.机械工程学报（Chinese Journal of Mechanical Engineering），2004，40（8）：115-118.

［17］李天云，赵研，韩永强，等（Li Tianyun，Zhao Yan，Han Yongqiang，et al）.Hilbert-Huang变换方法在谐波和电压闪变检测中的应用（Application of Hilbert-Huang transform method in detection of harmonic and voltage flicker）［J］.电网技术（Power System Technology），2005，29（2）：73-77.

Detection and Analysis of Power Quality Disturbances Based on LMD and TEO

ZHOU Chao，HUANG Chun
（College of Electrical and Information Engineering，Hunan University，Changsha 410082，China）

The causes of the deficiencies of local mean decomposition（LMD）in the disturbance detection at the positioning time is analyzed.An energy operator demodulating approach based on LMD is applied to the detection and analysis of power quality disturbance signal.The method consists of LMD and Teager energy operator（TEO）.Firstly，voltage signal is decomposed into a number of product functions（PFs）by LMD，then TEO demodulates the PF components to get the instantaneous amplitude envelope and instantaneous frequency of the signal.According to the frequency mutation point of time-frequency diagram，the starting and ending time points of the disturbance can be effectively located.Compared with the LMD method，the proposed method has accurate detection results for magnitude and frequency of disturbance signal，strong positioning capability and less end distortion，showing that it can effectively detect the nonstationary power quality disturbance signals.

local mean decomposition（LMD）；product function；Teager energy operator（TEO）；power quality；signal processing

TM712

A

1003-8930（2016）09-0014-06

10.3969/j.issn.1003-8930.2016.09.003

周超（1990—），男，硕士研究生，研究方向为电气信号检测。Email：935850757@qq.com

2014-09-25；

2015-11-30

国家“863计划”资助项目（2012AA050215）；国家电网公司科技项目（5216A313500N）

黄纯（1966—），男，博士，教授，博士生导师，研究方向为电能质量分析与控制。Email：yellowpure@hotmail.com