基于Steinmetz理论的三相四线制不平衡电流补偿

王江彬，田铭兴，陈　敏，赵远鑫

（兰州交通大学自动化与电气工程学院，兰州 730070）

基于Steinmetz理论的三相四线制不平衡电流补偿

王江彬，田铭兴，陈敏，赵远鑫

（兰州交通大学自动化与电气工程学院，兰州 730070）

由于零序分量的存在，三相四线制电路的不平衡补偿问题较三相三线制电路更复杂。该文基于Steinmetz理论的对称分量分析法考虑三相三线制系统负荷的平衡化补偿思路给出了三相四线制系统负荷不平衡电流的补偿方法，并给出3种约束方程下的补偿电纳模型。在三相四线制系统中，在已找到的3种约束方程条件下，对Y型联接的负荷进行零、负序电流补偿，并使系统功率因数提高到1。最后通过Matlab仿真表明，所提补偿理论不仅能实现不平衡电流的平衡化，还能使系统总功率因数接近于1，证明了所提补偿理论的正确性。

对称分量分析法；三相四线制；约束方程；零、负序电流补偿

在中、低压配电系统中，很多因素会造成配电系统三相不平衡［1-5］，从而导致供电系统的三相电压、电流不平衡。不平衡的三相电流不仅会产生大量无功，而且会产生负序电流分量，继而影响电力系统的安全运行。在三相四线制系统中，不平衡电流还会产生零序电流分量，也会对电力系统产生众多不利影响。

当前，绝大多数的不对称补偿问题研究都是针对三相三线制系统进行的，通常只考虑系统存在负序电流分量的情况，很少对三相四线制系统中零序电流分量的不对称补偿进行研究［6］。

Steinmetz理论只适用于三相三线制系统的不平衡电流负序补偿，但是其核心思想却可以推广应用到三相四线制系统的不平衡电流负序和零序补偿研究中。

本文应用Steinmetz理论的核心思想考虑了三相四线制系统中的不平衡电流补偿问题，对三相四线制系统中Y型接线负荷的零、负序补偿方法相关的公式作了推导。在3种约束方程条件下，使系统零、负序补偿后功率因数提高到接近1。最后通过Matlab软件验证了补偿理论的正确性。

1　补偿理论公式推导

对于一个三相四线制系统，由于中性线不接地的Y型负荷可以通过Y-Δ转换变成Δ型负荷，所以无论其负载有多复杂，都可以将其等效成如图1所示的连接在一起的Δ型负荷与带有中性线的Y型负荷。在图1中，分别为a、b、c三相以及中性线相对于中性点的电压相量。为流入Y型负荷各相的电流相量，为流入Δ型负荷各相的电流相量。为Δ型连接负荷的负荷导纳，为中性线接地的Y型连接负荷的负荷导纳。下文相同参数代表相同的意义。

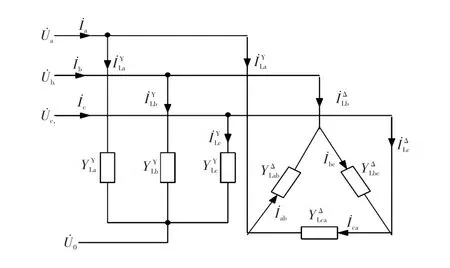
图1　任意负载的等效Fig.1　Equivalence of an arbitrary load

对于这种负荷进行补偿时，既要设置负序补偿器，又要设置零序补偿器。对于Δ型负荷，由于它不会产生零序电流分量，其产生的负序分量可以用Steinmetz负序补偿理论消除。中性线接地的Y型负荷则不同，它在电力系统中不仅会产生负序电流分量，还会产生零序电流分量。鉴于在Steinmetz负序补偿理论中用Δ型补偿器补偿Δ型负荷的思想，这里用Y型补偿器来补偿中性线接地的Y型负荷。补偿原理图如图2所示。

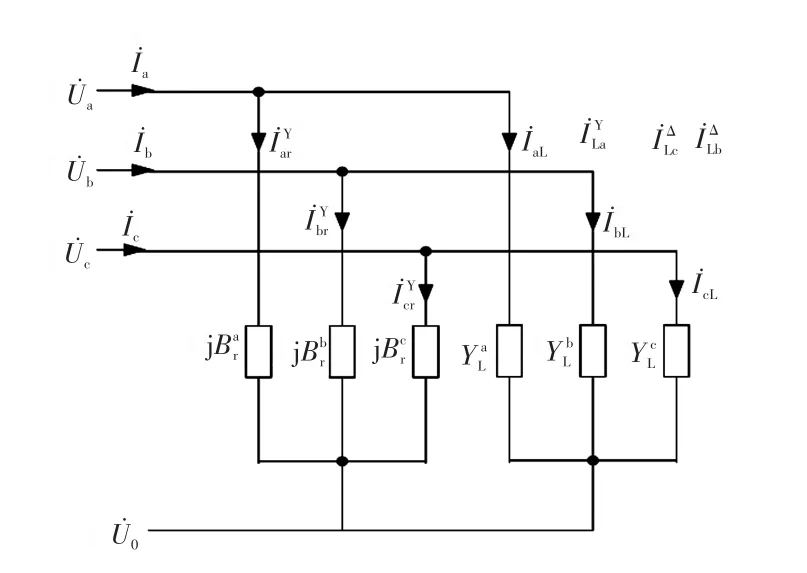
图2　三相四线制下仅用Y型负荷补偿原理Fig.2　Compensation principle of only using star-connected load under three-phase fourwire conditions

要使系统零、负序完全补偿且使得系统功率因数达到1，则要满足：

式中：下标（0）表示电流量的零序分量；下标（1）表示电流量的正序分量；下标（2）表示电流量的负序分量。

该方程可以进一步化成为

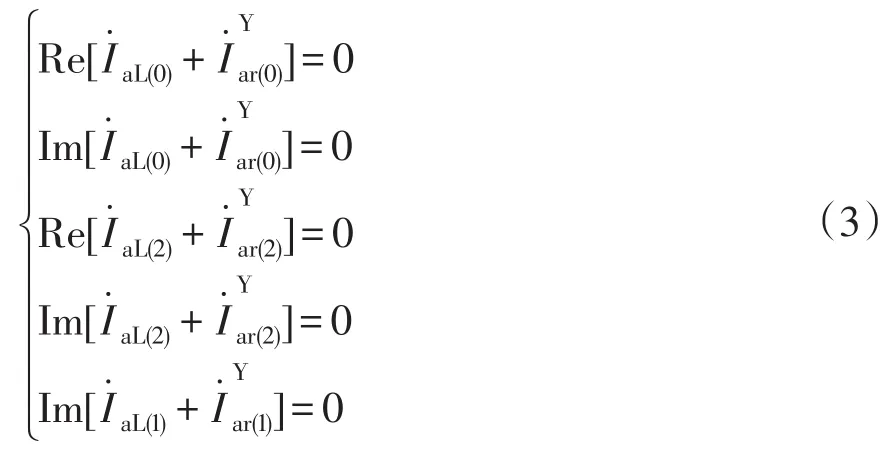
容易观察该方程有5个方程却只有3个未知数，所以方程组为超定方程组。一般情况下，超定方程没有古典意义下的精确解。目前有很多求解超定方程的算法，但这些算法都异常复杂且很难求出方程的精确解。为了使方程组成为恰定方程组，在补偿时再加设Δ型补偿器。补偿原理图如图3所示。

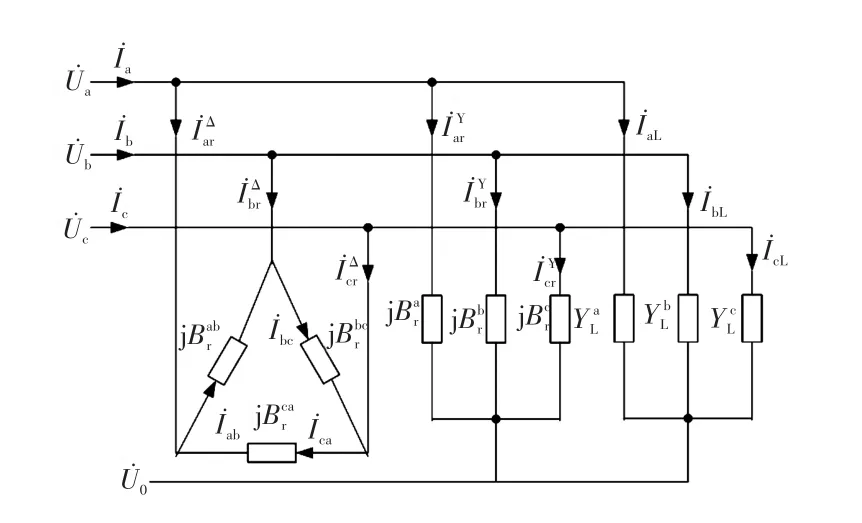
图3　三相四线制下用Δ型和Y型负荷补偿原理Fig.3　Compensation principle of using delta-connected compensator and star-connected load under threephase four-wire conditions

要使系统零、负序完全补偿且使得系统功率因数达到1，则要满足［7］为

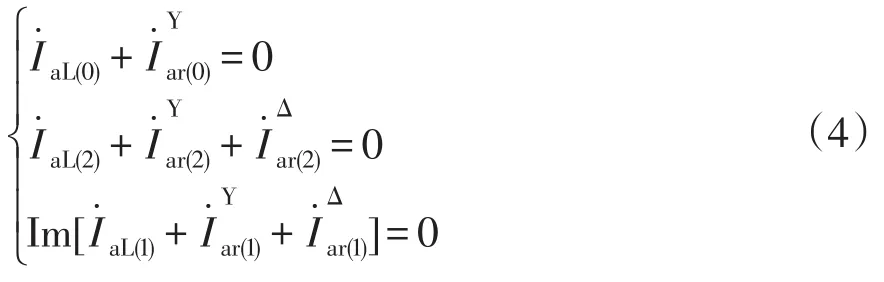
该方程可以进一步化成：

该方程有5个方程却有6个未知数，这时方程为欠定方程，为了使方程成为具有唯一解的恰定方程，必须另外找到一个方程。

1.1零序和负序补偿的理想补偿网络模型

对于图2所示的补偿系统，由文献［6］得：

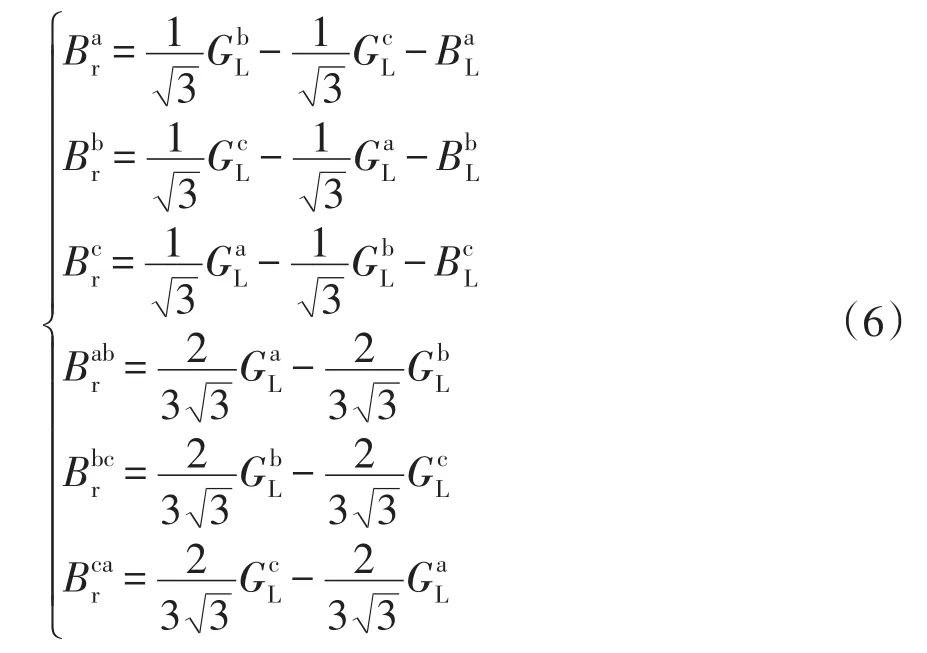
式（6）为三相四线制系统中只有带中性线Y型负荷的零、负序理想补偿网络模型。这种补偿模型只能用来说明补偿原理，由于这种补偿模型的补偿电纳用负荷导纳表示，不容易测量，所以该模型不实用。下面用对称分量法分析这种负序、零序补偿原理。

1.2对称分量法表示的零序和负序补偿模型

忽略不平衡负荷对负荷电压的影响，假定补偿前后系统负荷的三相电压完全对称，即负荷电压为三相对称正弦电压。

这样就可以求出负荷的三相电流为

当选择a相作为基准相时，三相负荷线电流与其对称分量之间的关系表示为

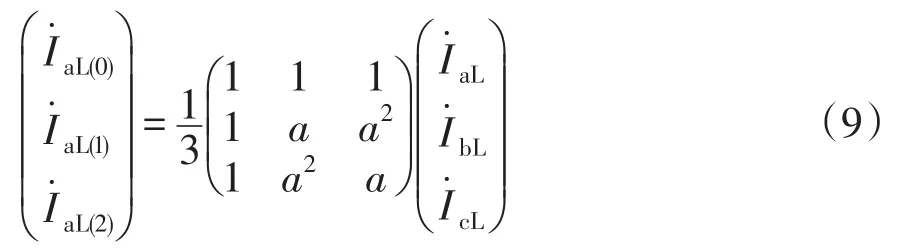
（1）Y型负荷的对称分量有：

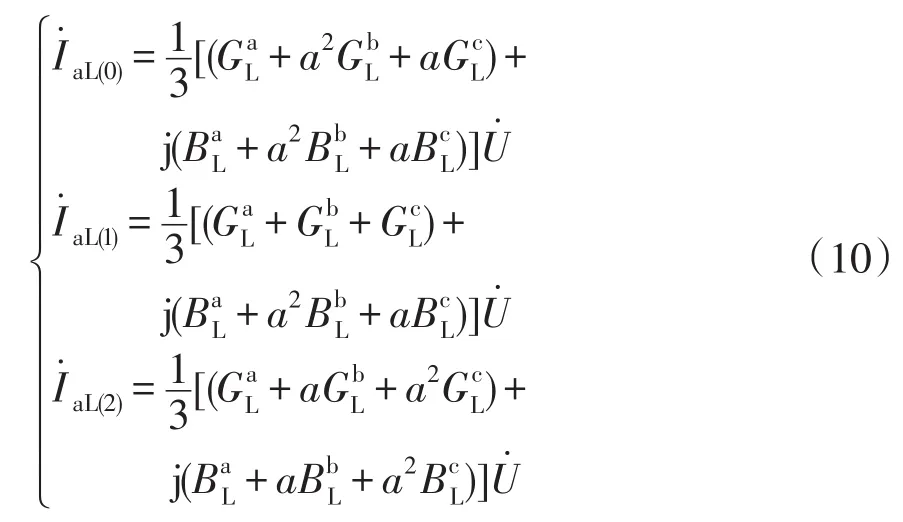
（2）Y型补偿器的对称分量有：

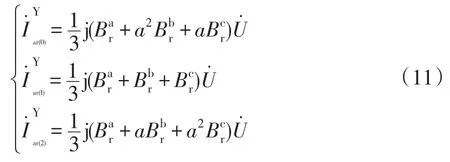
（3）Δ型补偿器的对称分量有：

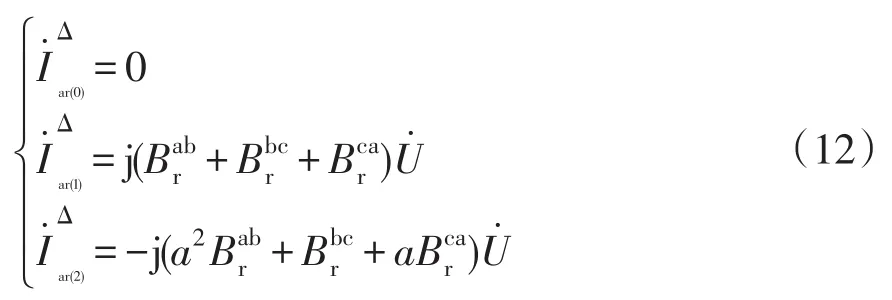
要使系统的负序和零序消除且使功率因数为1，就要满足式（4）给出的条件。

则可得：

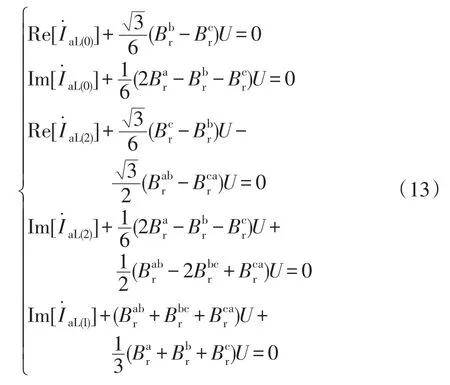
下面在已经找到的3种约束方程条件下求零、负序补偿模型。

1.2.1第1种约束方程下的补偿电纳模型

即满足：

要满足式（4）中的第3式，则要满足：

即满足：

式（16）即为找到的一个约束方程。这时式（4）的条件就可以改为

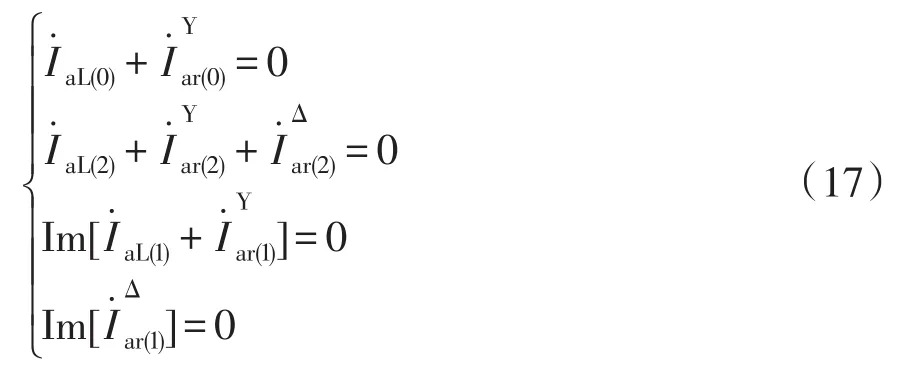
则可得：

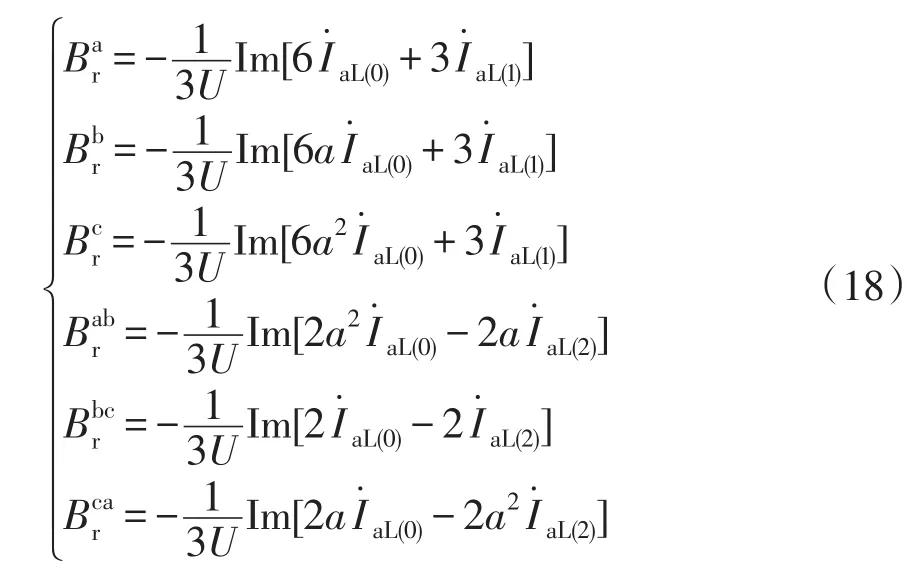
化成矩阵形式为

其中

将该矩阵应用线电流对称分量表达式（9）化成相电压和线电流来表示补偿电纳的矩阵表达式为

其中

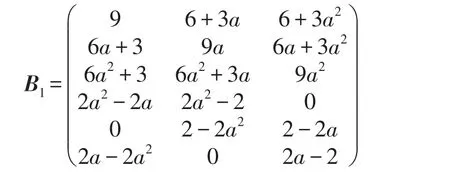
1.2.2第2种约束方程下的补偿电纳模型

要满足式（4）中的第3式，则要满足：

即满足：

式（23）即为找到的另一个约束方程。这时式（4）的条件就可以改为

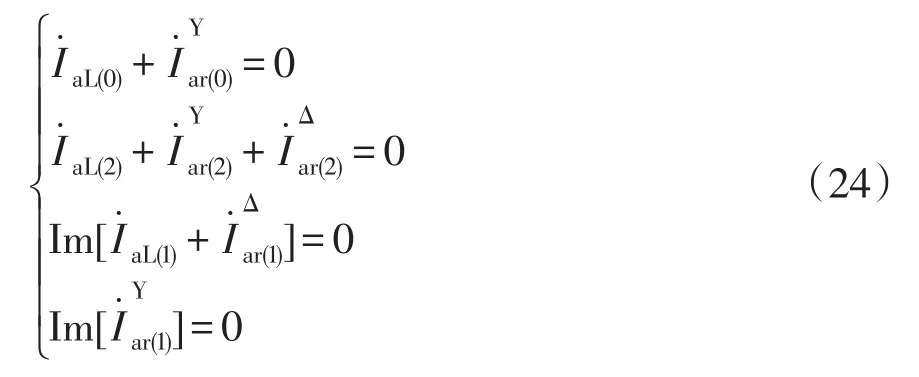
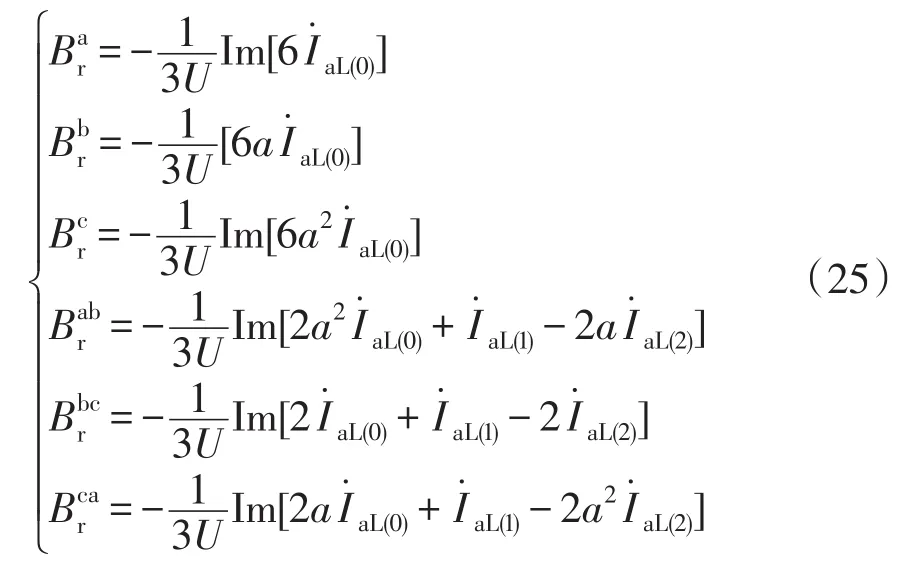
化成矩阵形式为

其中

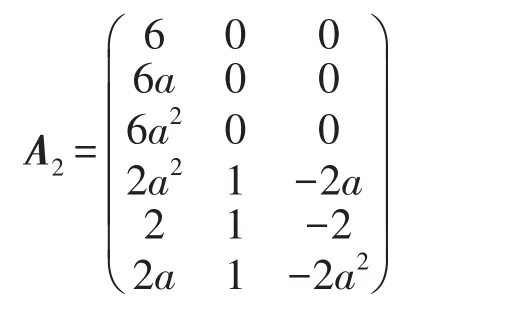
将该矩阵应用线电流对称分量表达式（9）化成相电压和线电流来表示补偿电纳的矩阵表达式为

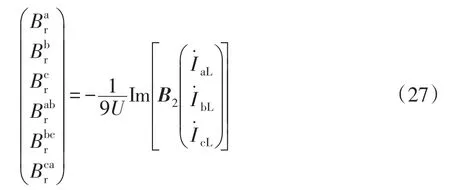
其中

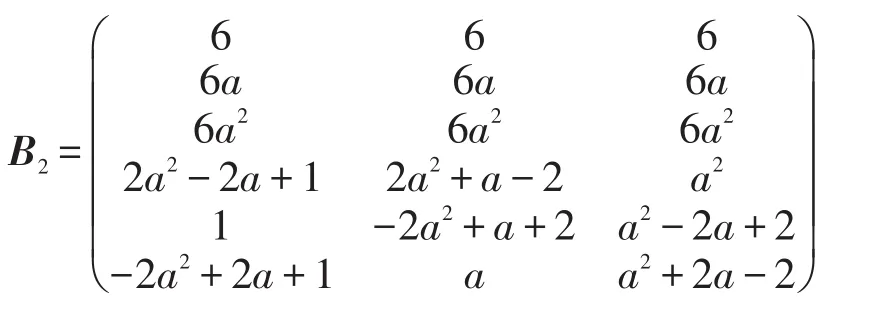
1.2.3第3种约束方程下的补偿电纳模型

从线路损耗的角度考虑补偿电流的大小，应使补偿电流平方和最小。现在采用三相补偿电流平方和最小这一约束条件，使补偿装置设置更简单［9］。

补偿器各相补偿电流的平方和为

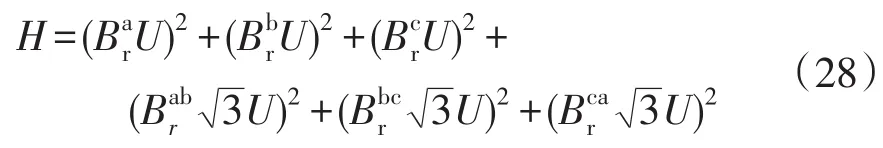
将式（10）、（11）与（12）代入式（4）中得：

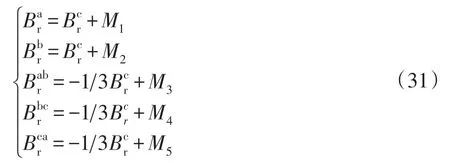
式中：M1、M2、M3、M4、M5均为常数。

由式（30）得：

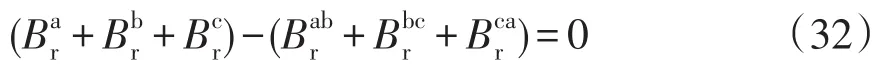
式（32）即为考虑补偿电流情况下的另一约束方程。这时式（4）的条件就可以改为

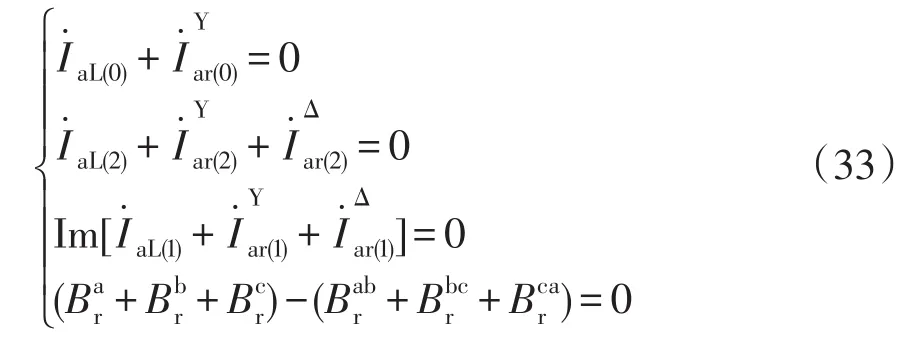
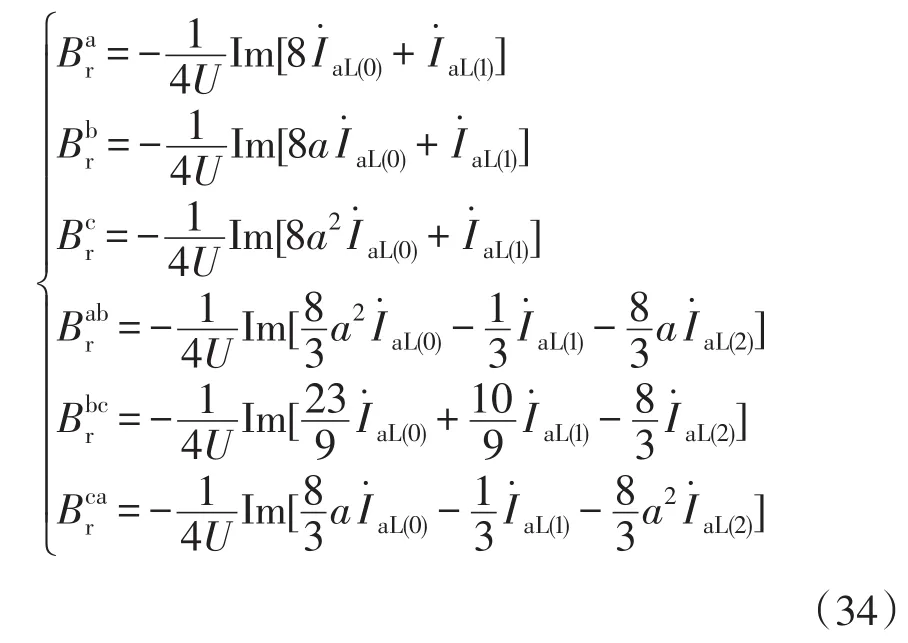
化成矩阵形式为

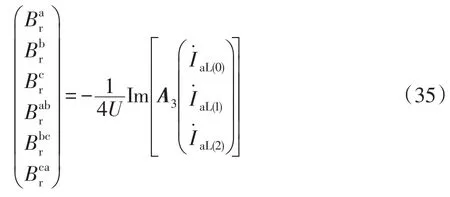
其中

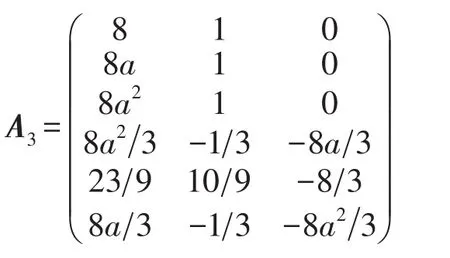
将该矩阵用式（9）化成相电压和线电流来表示补偿电纳的矩阵表达式为

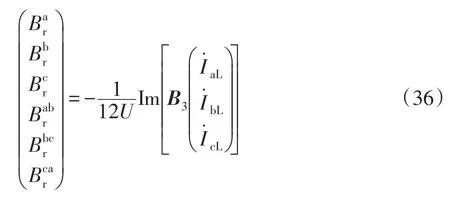
其中

以上考虑的是在三相四线制系统中只有中性线接地Y型负荷的情况。对于既有Δ型负荷又有中性线接地Y型负荷的情况，可以将Δ型负荷的负序补偿电纳和Y型负荷的零、负序补偿电纳叠加，这样就可以得到三相四线制条件下既有Δ型负荷又有中性线接地Y型负荷的零、负序补偿网络模型。

2　仿真分析

现在用Matlab对式（20）、（27）、（36）的正确性进行仿真分析。设电源电压三相对称，三相电压有效值为220 V。在进行仿真时，a、b、c三相的负载设置为感性负载，分别为这样设置后，测得三相线电流相量分别为未加补偿器时的三相线电流波形如图4所示。

应用式（20）计算出补偿器的补偿电纳，这样求得的补偿参数设置为。加补偿器后的三相线电流波形如图5所示。

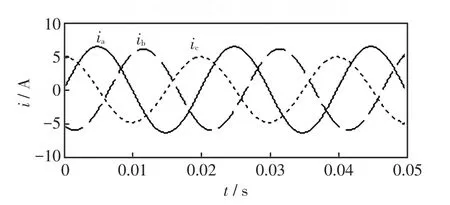
图5　第1种约束方程下补偿后三相线电流波形Fig.5　Three-phase current waveform after compensation under the first constraint equation

图5的仿真图表明补偿后，系统的电流基本达到平衡状态。通过Matlab测量三相电路功率因数的仿真图如图6所示。

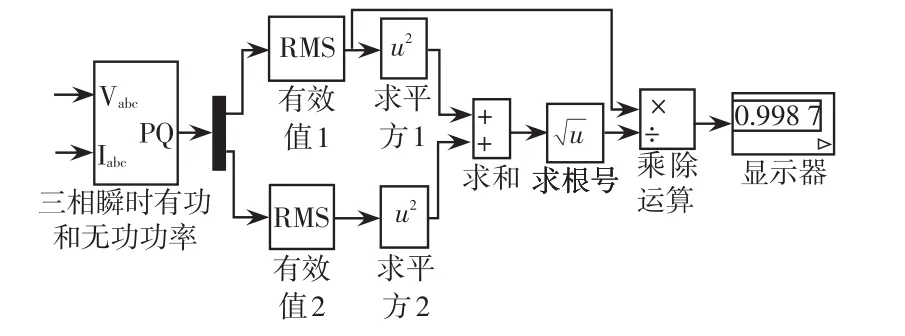
图6　第1种约束方程下的功率因数仿真Fig.6　Simulation of power factor under the first constraint equation

从图6的仿真图中可以看到补偿后系统的功率因数等于0.998 7。由于计算误差等各种原因，就是在理论条件下，补偿后的结果也很难达到1。但仿真得到的这样的功率因数对于工程实际已经非常高了。

同理可以分析在第2种和第3种约束方程下，补偿后系统的电流基本达到平衡状态，系统的功率因数也接近于1。

3　结语

在三相四线制系统中，在已找到的三种约束方程条件下，对只有中性线接地Y型负荷的情况推导了用相电压和三相线电流表示的补偿电纳公式。最后的仿真结果表明，在3种约束方程条件下，所推补偿电纳公式都能达到很好的补偿效果，证明了推导公式的正确性。

［1］胡应宏，王建赜，任佳佳，等（Hu Yinghong，Wang Jianze，Ren Jiajia，et al）.不平衡负载的平衡分量法分解及补偿方法（Balance component decomposition and compensation method for unbalanced load）［J］.中国电机工程学报（Proceedings of the CSEE），2012，32（34）：98-104.

［2］孙聪，王异凡，陈国柱，等（Sun Cong，Wang Yifan，Chen Guozhu，et al）.基于Steinmetz原理与瞬时无功理论的SVC装置防过补偿控制策略（Anti-overcompensation control strategy in SVC based on Steinmetz principle and instantaneous reactive power theory）［J］.机电工程（Journal of Mechanical&Electrical Engineering），2013，30（10）：1246-1249，1272.

［3］曾亚波（Zeng Yabo）.三相线间负载的无功和不平衡补偿实用算法（Research on practical comprehensive compensation algorithm for three-phase reactive power and unbalanced phase-to-phase load）［J］.电力电容器与无功补偿（Power Capacitor&Reactive Power Compensation），2010，31（5）：19-22，28.

［4］程振龙，唐晓骏，任慧，等（Cheng Zhenlong，Tang Xiaojun，Ren Hui，et al）.考虑电压稳定约束的无功补偿优化配置（Optimal configuration of reactive power compensation considering voltage stability constraints）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（4）：86-91.

［5］佘双翔，张志文，刘舜，等（She Shuangxiang，Zhang Zhiwen，Liu Shun，et al）.新型曲折接线负荷平衡变压器及其特性分析（Novel zig-zag load balance transformer and its characteristics analysis）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（10）：34-40，47.

［6］单铁铭，杨仁刚（Shan Tieming，Yang Rengang）.不平衡电流无功补偿方法研究（Reactive power compensation for unbalanced current）［J］.电力自动化设备（Electric Power Automation Equipment），2004，24（12）：26-29.

［7］Lee San-Yi，Wu Chi-Jui.On-line reactive power compensation schemes for unbalanced three phase four wire distribution feeders［J］.IEEE Trans on Power Delivery，1993，8（4）：1958-1965.

［8］Lee S-Y.Reactive power compensation and load balancing for unbalanced three-phase four-wire system by a combined system of an SVC and a series active filter［J］.IEEE Proceedings-Electric Power Applications，2000，147（6）：563-578.

［9］廖培，刘会金（Liao Pei，Liu Huijin）.三相四线制条件下的不平衡电流无功补偿（Unbalanced currents and reactive power compensation for three-phase four-wire）［J］.电力电容器（Power Capacitor），2007，28（4）：10-12，21.

Three-phase Four-wire Unbalanced Current Compensation Based on Steinmetz Theory

WANG Jiangbin，TIAN Mingxing，CHEN Min，ZHAO Yuanxin
（School of Automation and Electrical Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China）

Because of the existence of zero sequence components，the unbalanced compensation of three-phase fourwire system is more complicated than that of three-phase three-wire system.The compensation method of symmetrical component analysis method based on Steinmetz theory in three-phase three-wire system load balancing compensation is considered in the three-phase four-wire system unbalanced load current compensation.Moreover，the compensation model of three kinds of constraint equations is given.In the three-phase four-wire system with the three above constraint equations，attempts are made to compensate the zero sequence and negative sequence current for star-connected load，and increase the system power factor to 1.Finally，the Matlab simulation results show that the proposed compensation theory can not only keep the unbalanced current balanced，but also make the power factor of total system be equal to 1 approximately，which proves the correctness of the proposed compensation theory.

symmetrical component analysis method；three-phase four-wire system；constraint equation；zero sequence and negative sequence current compensation

TM714.3

A

1003-8930（2016）09-0020-07

10.3969/j.issn.1003-8930.2016.09.004

王江彬（1990—），男，硕士研究生，研究方向为功率理论以及不平衡电流补偿。Email：1550151867@qq.com

田铭兴（1968—），男，博士，教授，研究方向为电力系统电能质量分析及其综合治理、电力电子技术及其应用、电机电器及其控制。Email：tianmingxing@mail.lzjtu.cn

陈 敏（1990—），女，硕士研究生，研究方向为功率理论及不平衡电流无功补偿。Email：409245873@qq.com

2014-09-12；

2016-03-18

国家自然科学基金资助项目（51167009）；国家自然科学基金资助项目（51367010）；甘肃省科技计划资助项目（1304WCGA181）；兰州市科技计划资助项目（2013-4-111）