数学建模在数据处理与仿真的应用
2016-10-25李佳彤于晓航宋阳
◎李佳彤 于晓航 宋阳
数学建模在数据处理与仿真的应用
◎李佳彤 于晓航 宋阳
本文主要针对嫦娥三号着落过程中粗、精避障问题,基于已有算法完成了着陆位置的选取任务。进而优化了算法,突破性的预先排除深坑、大坑等不利地形,避免为月球车进一步开展工作造成障碍;同时开创性的更新了算法流程,上百倍的缩小了程序运算时间。我们采用基于高程图数据的危险区扫描识别方法,通过计算扫描区域的粗糙度和坡度来判别地貌、识别危险区,然后扫描计算每一选定区域的粗糙度值、坡度值和相对目标着陆点的距离等因素来加权生成该点着陆成本图,最后根据成本图优选着陆点,仿真计算结果表明,该方法能够快速识别最优着陆点。
模型建立
记嫦娥三号着陆器矩形边长为s,为了提高着陆安全性,考虑控制误差,应使着陆点附近控制误差范围内的地形也符合安全着陆要求,因此,确定最小计算单位为3s个网格。按栅格化扫描模式开始扫描,对每一个扫描区:计算3s个网格内的所有规则样点的方差δ,作为该网格的粗糙度。然后将3s个网格平均划分成九个小的单位s*s,取出每一个小单位的角位置的四个点,任取三个点可以组成一个平面,计算这个平面与月球的水平面的夹角α。可以得到四个坡度值 1α , 2α,3α,4α,在每一个小单位中都可以得到相应的1iα,2iα ,3iα ,4iα ,求对应的的α均值,作为该扫描区域的坡度值。以逐行扫描的方式,每次移动三个网格,进行相同的计算过程,当计算完一列后,向右侧移动一列,完成整个区域的扫描计算。然后,计算每一个网格到预定着陆点的水平距离,生成一个距离矩阵R。
在选择最优着陆点之前,将得到的粗糙度图、四个坡度图和距离图归一化。根据给定的着陆器安全着陆的最大粗糙度maxδ、坡度maxα和着陆器最大水平机动距离maxR,若δ(i,j) >δm ax 或α(i,j)>αm ax 或R (i,j) >Rmax ,则将该网格内的值设置成1,并且,以该点为中心的s个网格内的值均设置成1,以保证着陆器在着陆过程中,不会与危险区中的障碍物相撞。从而,生成归一化的粗糙度图、坡度图和距离图。
根据对预定的着陆区域附近地形的初步分析(任务开始前已由地面地形分析给出),可以设定粗糙度、坡度和距离在最优着陆点选择中的权值a,b,c。由公式
得到着陆区域的着陆成本图数据,最低点即为选出的着陆点。
模型分析
基于上文的理论分析,我们进行了仿真模拟。首先考虑到粗避障的精度需求,我们选取了100*100的扫描单位。在附件中给出的“距2400m处的数字高程图”中读取数据进行扫描,我们最优的得到了一块基于完全平整的区域,高度值基本为0m,在这块区域中粗糙度和坡度基本为零,可以认为是完美的落地区域。但是我们没有盲目的确认落地点而是进行了其他方式的测验,结果把高程图重新在MATLAB中绘出三维立体旋转图后我们发现,原来我们在月球表面的降落区域掉到了一个“大坑”里面,坐标为x=1014,y=234(见Fig 1蓝色最深区域)。这样的位置即使我们可以确认其相当“平坦”,但是有两个无法避免的弊端:其一月球车一旦降落在其中,很难爬坡出来进行勘测;其二月球车在下降的过程中,很容易撞击到周围的“山峰”——红色环形。因此我们需要首先在高程地图上面把这些“大坑”排除。这就是本算法首先值得优化也是必须要优化的地方。
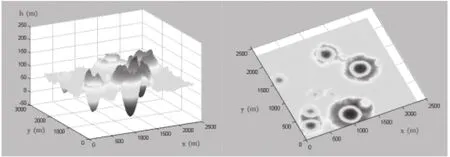
Fig1 距月2400m处的数字高程图在MATLAB下绘制的三维图像
另外,在运算过程中我们进一步的优化了粗糙度的定义方式以及更新算法流程,将算法运行时间大大减小。
模型优化
避开“大坑”。当遇到大的陨石坑时,粗糙度会变得巨大,可以直接将其剔除,使其不在后来的系数计算中被考虑。具体方法是在计算出各个位置的粗糙度后,将明显过大的区域的D(粗糙度)值设为无穷大,这样在后续的运算中就不会参与计算,因此剩下参与运算的位置就是所有所有不包含大陨石坑的点。这样的方法将会良好的避免了之前我们出现的将嫦娥三号降落在大坑中的情况。
优化运行时间。改进一:取高程图中ap,q是从ai,j到中间枚举的所有元素,每次仅代表一个元素,范围在ai,j到ai+3s-1,j+3s-1中变化。在粗避障中,s取基本扫描单位100格,基础的方差公式为

在公式中由于要每次计算除以2s,一方面增加运算使运行速度下降;另一方面,除法产生了小数,使最终精度会受到影响。因此我们改进了D的定义

这样成功的降低运算速度并且提高精度。
改进二:在计算一个扫描区域的粗糙度即方差时需要用到该区域的平均值或和值Aall,因此需先计算每个扫描区的和值。从Fig 1中我们看到,空心小圆圈表示高程图中的数据点,在“距2400m处的数字高程图”中有2300*2300个数据点。红色小方框代表上一次用来计算的区域,黑色小方块代表下一时刻计算和值的区域,在不断的平移中我们记录所有的和值并且按照上式进行计算。在这里发现其中有重复的运算。为了简化,每次我们不重新计算黑色方框中的数据点,而是采用减去前一列再加上后一列的方式,这样看似简单的运算实际上大大简化了运算复杂程度。

硬算的话需要时间复杂度
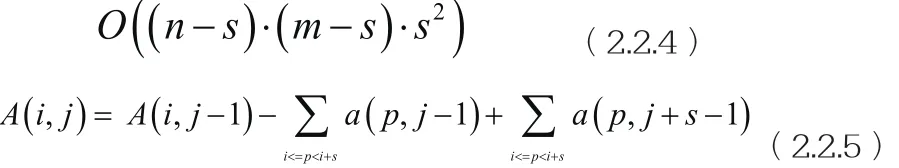
可以发现当j2=j+s时,相同,所以存在重复计算,因i<=p 这样计算A的总体时间复杂度就在预处理阶段,发现pA(i,j)与pA(i+1,j)只有开头和末尾的元素不同,存在重复计算,因此只需计算所有pA(1, j),然后 对于粗避障阶段: 对于精避障阶段: 可见均有max(m·s,(n-s)·(m-s))=(n-s)·(m-s)。因此计算A的总的时间复杂度从O((n-s)·(m-s)·s2)降为了O((n-s)·(m-s)) 改进三:受到A的改进的启发,在接下来计算粗糙度即方差D时,希望也能由D(i,j-1)得到D(i,j),优化重复计算的部分。 为此,将重定义的D展开: pD(i,j,0)和pD(i,j,1)是预处理数组,预处理复杂度为O((n-s)·(m -s)·s ),同改进二中对pE的处理方法,pD可以优化到O((n-s)·(m-s )),然后可以利用上式在O((n-s)·(m-s))内计算完所有D,所以整个复杂度从O((n-s)·(m-s)·s2)降为了O((n-s)·(m-s)·s )。 通过以上三个角度的改进,算法整体复杂度从O((n-s)·(m-s)·s 2)降为了O((n-s)·(m-s)·s ),进而我们进行的仿真模拟。原始算法在扫描单位为100*100的条件下需要运算1497.431(s),经过以上的算法优化的方式得到的优化后运算时间为60.431(s),时间减小两个量级,为原来的0.0404。优化效果显著。 权重因子显然是算法中相当重要的一环。设置比例合适的粗糙度、坡度、距离三个因素的权重因子,计算每个不包含陨石坑的扫描范围的加权成本值,从中选择成本最小的位置作为着陆点即可完成粗避障阶段的策略选择。优秀的权重因子的搭配将会提供降落位置的优秀策略,而不合适的权重因子则会导致诸如:耗费燃料、粗糙度小但陡峭、不陡峭但粗糙等等情况,给降落带来困难。 关于权重因子的确定:为了方便观察和计算,三个加权值应该处于同一个数量级上,所以首先约定三个影响因素的值与对应权值的乘积都在0.110量级上。据此,初步根据三个因素的平均值定义权值,分别为qD=1e-15,qDis=1e-6,qSlope=1,初次计算出对应的着陆位置后,三者加权值为: qD*D=0.002243 qDis*Dis=1.250293 qSlope*Slope=0.739042 Fig3 粗避障选择的粗略着陆 比较发现依然相差过大,很容易导致着陆位置不合适,而此时找到的位置为:(2179,1398),由图也观察到此处并不适合着陆。如图所示在一个大坑旁边,不适合降落。 此阶段坡度影响应大于粗糙度,大于距离,所以再次调整三个权重,使得qD=1e-13,qDis=1e-7,qSlope=1,再次运行程序,此时结果为: qD*D=0.220227 qDis*Dis=0.143785 qSlope*Slope=0.687549 min_cost=qD*D+qDis*Dis+qSlope*Slo pe=0.6875491.051560 着陆点:(1875,185) 由图可以看到,此位置十分合适。证明了本算法的正确性。 完成以上改进,我们做了完整的粗避障模拟。最终由计算机判断着陆成本Q取最小值初步得到粗略着陆位置x=1875,y=185。成本Q值为0.6875491.051560,权重系数 qD=1e-13,qDis=1e-7,qSlope=1,选择 位 置 的 相 对 粗糙 度 为qD*D=0.220227, 相 对 坡度为 qSlope*Slope=0.6875491.051560,相对距离qDis*Dis=0.143785,实际横向移动距离为1199.1038m,运行时间run time:60.856 s。直观地从图中也可看出,在红旗着陆区起伏高度(颜色)是最均匀的,不仅避开了所有的“大坑”而且显然易于降落,也利于降落后进一步开展勘测工作。 Fig4 粗避障选择的粗略着陆位置 精避障阶段的避障策略采用的算法与粗避障阶段基本保持一致,但是需要修改的变量有:扫描单位30s=,扫描分为是3s,降落区域大小为100m*100m,权重因子也相应改变即粗糙度、坡度和距离的权重分别为0.45、0.45、0.1。最终由计算机判断着陆成本Q取最小值初步得到粗略着陆位置x=191,y=0。降落安全范围为191≤x≤281,0≤y≤90大小是9平方米的区域。成本Q值为2.152388,权重系数qD=1e-13,qDis=1e-7,qSlope=1,选择位置的相对粗糙度为qD*D= 0.832249,相对坡度为qSlope*Slope= 1.292611,相对距离qDis*Dis= 0.027528,实际横向移动距离为52.60 m,运行时间run time: 9.750 s。直观地从图中也可看出,在红旗着陆区起伏高度(颜色)是最均匀的,由于中心区域有一个大坑,不适宜降落,加之我们适度调低了距离的权重(消耗燃料极少)。因此模拟结果最终选择了一个看似较为偏远,但是粗糙度和坡度搭配最为合理,整体降落成本Q值最小的区域降落。在图中由小红旗标出降落地点。 (作者单位:北京师范大学) Fig5 精避障区域示意图和选择的精确着陆位置
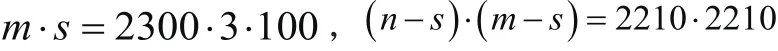

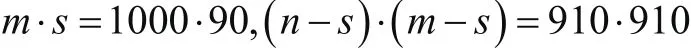
权重因子确定
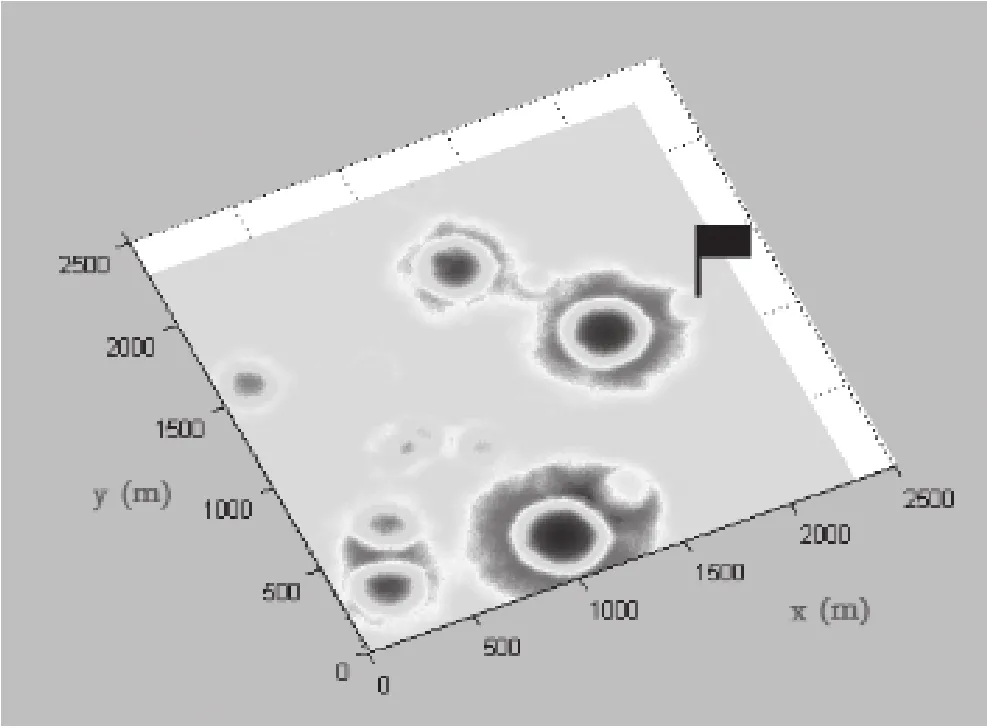
粗避障阶段仿真结果

精避障阶段仿真结果