高等数学中的极限

陈　星，徐加波，樊小琳

（新疆工程学院 基础教研部，新疆 乌鲁木齐 830091）

高等数学中的极限

陈星，徐加波，樊小琳

（新疆工程学院 基础教研部，新疆 乌鲁木齐 830091）

极限概念是高等数学的一个最基础的概念。文章主要探讨了极限的发展、科学内涵，并且比较了Cauchy和Weierstrass关于极限的定义。最后讨论极限中有关术语的含义及其易犯的错误。

极限；变量；无限变化；“［ε-N］”语言

极限是高等数学学习的基础，也是研究微分学和积分学的必备工具。微积分中的连续、导数、积分、级数等概念都是建立在极限的基础上。极限也是初学高等数学者遇到的第一个非常重要却高度抽象难理解的概念。因为它用有限的形式来叙述变量无限变化的过程。但能否对数列极限概念有深刻的理解，直接关系到今后学习高等数学的成败。

1　极限概念的发展

1.1朴素极限思想的萌芽

朴素极限思想的产生到严格极限概念的建立大约经历了两千年。从公元前五世纪开始，一些古代的哲学家和数学家在研究关于无限性的哲学问题和数学问题时，已经产生了一些朴素极限思想。如：古希腊雅典时期的形而上学学者Zeno在对无限性、连续性问题进行探索时，提出了“神行太保”，即Achilles永远追不上乌龟的悖论，尽管这是一个明显错误的结论，但在没有极限概念的古代，这个问题是难以解释清楚的；古希腊雅典时期的诡辩学派的代表人物Antiphon为解决“化圆为方”问题，首先提出了用圆的内接正多边形面积来逼近圆面积的思想，该思想后来被古希腊数学家Archimedes用于求抛物线图形的面积；公元前3世纪，根据我国古代《庄子·天下篇》中记载，梁国宰相惠施说过：“一尺之棰，日取其半，万世不竭”，其描述的也是一个趋于零而不等于零的无限过程；我国魏晋时期的数学家刘徽在对《九章算术》作注中提出“割圆术”作为计算圆周长、圆面积及圆周率的基础，其思想也是用圆的内接正多边形逐步逼近圆。

1.2极限概念的发展

17世纪下半叶，Newton和Leibniz在前人工作的基础上，分别以运动学和几何学为背景各自独立创立了微积分。微积分的诞生和发展，不但迎来了数学上的一个空前繁荣的时期，而且大大拓展了数学的研究范围。但是Newton和Leibniz建立的微积分是不严格的，其在发展和应用过程中出现了很多错误和悖论。其中英国的唯心主义哲学家——G.Berkeley指出，Newton和Leibniz的微积分中包含了“偷换假设”的逻辑错误，他攻击Newton流数论中关于无穷小量的混乱假设。他的批评是击中要害的，问题的核心就是什么是无穷小量。而当时Newton没有能严格说清楚极限的含义。直到1821年和1823年Cauchy在《分析教程》和《无限小计算教程概论》中对极限给出了较为明确的定义。即，一个变量逐次所取的值无限趋近一个定值，最终使变量的值与该定值之差要多小就多小，那么最后这个定值就称为所有其他值的极限。但极限的严格化概念最终应归功于德国数学家Weierstrass，他创造了一套ε-N（ε-δ）语言来建立极限的概念和理论。

2　极限概念的科学内涵

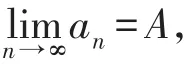
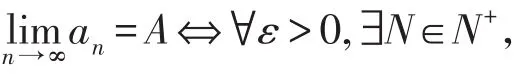
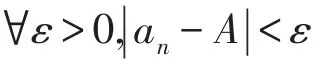
3　数列极限的几何意义

3.1在数轴上，|an- A|表示数列｛an｝的通项与A之间的距离，记作ρ（an，A），则数列极限也可简单的写成

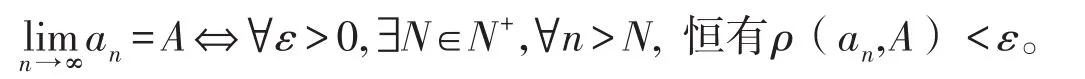
从而定义从几何上用距离ρ（an，A）的大小来刻画an与A的接近程度。只要n充分大，由ε的任意性与距离不等式ρ（an，A）＜ε就刻画了an与A能无限接近。

3.2在数轴上，|an-A|＜ε表示以A为中心，ε为半径的开区间（A-ε，A+ε）。记为U（A，ε），则数列极限也可简单的写作

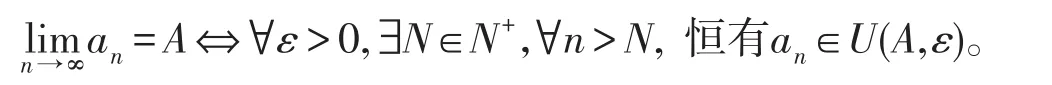
该定义表示，对于任给的ε＞0，总存在正整数N，使｛an｝中从N+1项开始的所有各项全部落入A的ε邻域中，在此邻域外最多只有｛an｝的前N项。只要n充分大，用邻域U（A，ε）的大小来刻画an与A的接近程度，用ε的任意性和an∈U（A，ε）来刻画an与A能“无限接近”。

4　极限中各变量及术语的科学内涵

为了加深对极限概念的理解，应注意以下几点：

4.1关于“ε”：ε（＞0）是任意给定的，可以任意小。给定之前是任意的，给定后就是一个常数，|an-A|＜ε刻画an与A的接近程度。

4.2关于“N”：N（an的脚标）是正整数，由ε确定，随ε而变，保证了使|an-A|＜ε成立所需要的n变大的程度。但N不唯一，因此N不是ε的函数。

4.3关于“恒有”：表示从第N项后所有的an都满足不等式|an-A|＜ε，不能只是有限项，也不能只是无限项，必须是全部。

4.4该定义只能用于验证A是否为｛an｝的极限，不能用于求极限。

对于上述的问题，初学者常会产生一些模糊不清的问题，出现一些错误。例如：

4.4.2对无穷多个ε＞0，存在n∈N+，当n＞N时，恒有|an-A|＜ε。

4.4.3对任给的ε＞0，存在n∈N+，当n≥N时，有无限多项an，使得|an-A|＜ε成立。

4.4.5将定义中的恒有“|an-A|＜ε”改为“|an-A|≤ε”。

对于第4个注意点验证的关键是对任意ε＞0，从满足不等式|an-| A＜ε出发，通过解不等式的方法求得使该不等式成立的N。

Weierstrass在定义极限时，由于ε的任意性，极限的ε-N（ε-δ）定义才能刻画极限的无限过程。但是，一旦ε给定以后，它就是一个确定的有限常数，因此求N∈N+，使得当n＞N时，恒有|an-A|＜ε成立就是一个确定的有限过程。给ε，就可以求得相应的N。由于ε是任意的，所以，这种有限过程就有无限多个，这样就将极限的无限过程分为无限多个有限过程。而对于每个有限过程，由于ε是一个确定的有限常数，因此，就能用代数方法求得使不等式|an-A|＜ε成立的有限正整数N∈N+，从而完成有限过程。又由ε的任意性，在ε不断变小的过程中就完成了对无限过程的刻画。

［1］严芹.关于高等数学中数列极限教学的思考［J］.廊坊师范学院学报（自然科学版），2013，2（13）：124-126.

［2］邢妍，赵若男.文化视角下的极限概念［J］.中国科技信息，2010，（15）：169-171.

［3］同济大学数学系.高等数学［M］.北京：高等教育出版社.

［4］马知恩，王绵森.高等数学疑难问题选讲［M］.北京：高等教育出版社.

Analyze the Concept of Limit in Advanced Mathematics

CHEN Xing，XU Jia-bo，FAN Xiao-lin
（Institute of Xinjiang Engineering，Fundamental Department，Urumqi，Xinjiang，830091，China）

The limiting concept is one of the most basic concepts in the advanced mathematics.In this paper，we mainly discussed the development and scientific connotation of the limit，and compared the definition of Cauchy with Weierstrass.Finally，we discussed the meaning of related terms and the easily-made mistakes in limit.

Limit；Variable；Infinite variation；“［ε-N］”language

O423.1

A

1008-9659（2016）03-0041-03

2016-08-20

自治区青年科技创新人才培养工程（项目编号：qn2015bs013）；高等学校大学数学教学研究与发展中心2015教学改革项目（项目名称：线性代数课程中培养学生创新思维、创新能力的研究与实践）。

陈星（1982-），女，陕西西安人，博士研究生，主要从事图论及其应用研究。