基于微小卫星的空间目标光学探测定位方法

高玉东，崔凯凯

（国防科学技术大学航天科学与工程学院，长沙410073）

基于微小卫星的空间目标光学探测定位方法

高玉东，崔凯凯

（国防科学技术大学航天科学与工程学院，长沙410073）

为实现空间目标的天基光学观测，利用双星定位原理，采用仅测角的观测方式，结合最小二乘法建立了双星几何定位模型。考虑到星点提取作为光学定位算法中的重要一环将直接影响最终的定位精度，因而针对就星图处理部分，分析了星图的灰度特点，采用阈值分割法进行了去噪处理，选取了几种质心法对星点进行提取，利用真实星图对提取结果进行比较，选出了形心法和阈值质心法2种较为可行的星点提取算法。通过仿真计算和蒙特卡洛误差分析结果可知，不考虑误差时，定位误差小于10-5m；考虑主要误差源时，定位误差小于100 m；且姿态误差对定位方法的精度影响最大，数值上可以达到总误差的0.9倍以上，速度误差的影响最小，只有总误差的1/30，可以忽略；定位误差近似呈高斯分布且误差的大小与误差源近似呈线性关系。由此可见，文章所建立的定位算法可以对空间目标实现较为精确的定位。

星点提取；双星定位；蒙特卡洛打靶；定位误差

空间目标的光学定位是天基光学监视的基础。由于其能耗低、精度高且易于小型化的特点，发展前景被广泛看好［1］。天基光学监视是通过星载相机对空间目标进行光学成像，从而完成对目标的识别、锁定和追踪，属于仅测角定位的范畴。

在星图处理及提取方面，贾辉等详细介绍了亚像素定位技术的发展［2-3］。Auer和Stone等人也在文献［4］中对质心法、中值法、导数搜索法、高斯拟合法等星点提取方法的原理和精度做了详细介绍。文献［5］采用了一种基于高斯函数的相关算法，得到的星点提取精度可达到0.7%像素，文献［6］介绍了一种Fourier相移法，精度达到1%像素。

就具体的观测定位模型而言，李骏等人详细介绍过立体定位的方法［7］。堪钊介绍过一种基于CCD星图星点间的像素距离与其对应的恒星角距离严格对应成比例的空间目标精确定位方法［8］。误差分析也有理论推导、数据仿真和实验验证［9-11］等几种不同的思路。

本文围绕着光学卫星几何定位算法，主要开展了四方面的工作：星图的处理，定位算法的建立以及算法的仿真验证和误差仿真分析。

1　星图处理

1.1星图灰度特性的提取及分析

图1是某光学观测卫星S1在2014年11月22日夜间拍摄到的真实星图，原始像素为960×576，经裁剪后变为860×520，后续的计算分析均基于图1进行。

图1　某监视卫星S1拍摄得到的原始星图Fig.1 Original image taken by surveillance satellite S1

利用Matlab程序中自带的图像读取和分析模块将星图数字化，得到各像素点的灰度信息。随机选取100×100像素点做灰度柱状图，结果如图2所示。

从图2中可以看出：背景噪声占据了整幅图像的绝大多数像素点，而被监测目标即有用的星点信息的只占很小一部分，加之目标的灰度级别要远远大于噪声和背景干扰，故可选用阈值法来对图像进行去噪处理。

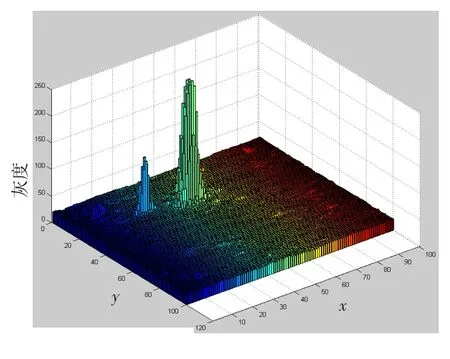
图2　原始星图的灰度统计结果Fig.2 Gray level statistic of the original image

1.2阈值去噪方法

由于星图处理的最终任务是提取星点的精确坐标，后续计算过程需要用到像点精确的灰度信息，这就要求尽最大的可能性保留目标星点的灰度分布信息［12］故在此采用如下去噪算法：

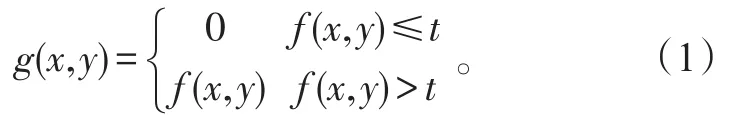
式（1）中：f（x，y）表示进行去噪处理前（x，y）处像素点的灰度值；t为灰度阈值；g（x，y）为去噪后（x，y）处像素点的灰度值，即去噪算法的最终求解结果。

利用迭代阈值法［12］计算最佳阈值。对已有星图进行计算得到最佳阈值为34。选择阈值34，按式（1）对星图进行去噪处理，去噪结果如图3所示。与图1比较，可以发现背景中的噪声基本上得到了抑制。

图3　经过去噪处理的星图Fig.3 Image after denoising

1.3几种改进的质心算法

星图上目标星点的能量是按一定规律分布在某一区域之内的，对星图做去噪处理后，背景区域的灰度值已经变为0。这样，为了方便计算，可将计算范围取为矩形区域，而不会对最后的提取结果产生影响。这里假设计算的矩形区域x坐标范围为［］m，n，y坐标范围为［］

p，q。几种改进的质心算法为：

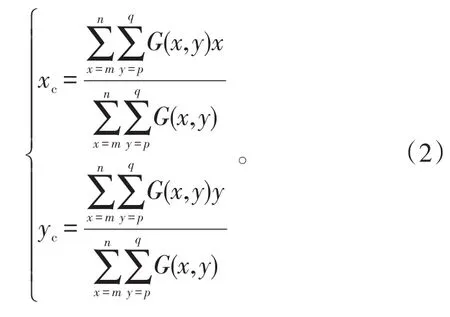
式（2）中：（xc，yc）表示星点的提取结果；形心法中，为去噪后，像素点上是否还有灰度值；灰度加权质心法中G（x，y）为g（x，y）；平方质心法中G（x，y）为g2（x，y）；阈值质心法中G（x，y）为g（x，y）-t。

在经过滤波处理后的星图中选取三颗最亮的恒星进行编号，视场中上方恒星标号为1，左下方恒星编号为2，右下方恒星编号为3，见图3。

利用天体之间的角距离与CCD星图中星点的像素距离严格对应成比例［3］的特点对本节中提到的星点提取算法进行验证和比较。结果如下：比值标准差越小，表示星点提取精度越高。当选择最佳分割阈值34时，形心法的星点提取精度比考虑灰度的质心法的精度要高。将阈值变为51、68，再次计算发现此时考虑灰度的质心算法精度均优于形心提取算法，这是由于考虑灰度的质心提取算法的计算结果会向亮度极值点靠拢，而亮度的极值点不会受到阈值改变的影响，因而对阈值的选择不如形心法敏感，其中又以阈值质心法的敏感性最低。这给我们的指导意义在于，如果可以有效地确定最佳阈值的数值，那么可以选用形心法进行星点提取；若无法确定阈值的选择是否准确，可以直接采用阈值质心算法进行计算。表1为精度比较时得到的部分计算数据。

表1　阈值取为34时星点提取精度比较Tab.1 Accuracy contrast of star point extraction when threshold is 34

2　定位模型的建立及仿真验证

2.1双星几何定位模型的建立

设目标成像的像素坐标为（xm，ym），则可知目标在测量坐标系中的单位方向矢量为dm=（xm，ym，f）/ρ，其中f为焦距，。利用V=IMdm将矢量dm转换到惯性坐标系下，其中，IM表示从测量坐标系到惯性坐标系的转换矩阵，V为惯性系中的观测矢量。则目标在惯性系中的位置坐标可以表示为r=Rj+ρjVj，j=1，2，其中，r=（x，y，z）表示目标位置；Rj=（Xj，Yj，Zj）表示监视星j在惯性坐标系中的位置；Vj=（lj，uj，vj）表示惯性坐标系中监视星的单位观测向量；ρj为实数，表示监测星到目标的距离。

将等式两端叉乘Vj，得到r×Vj=Rj×Vj，将向量等式整理成标量形式如式（3），得到了定位算法的求解方程：

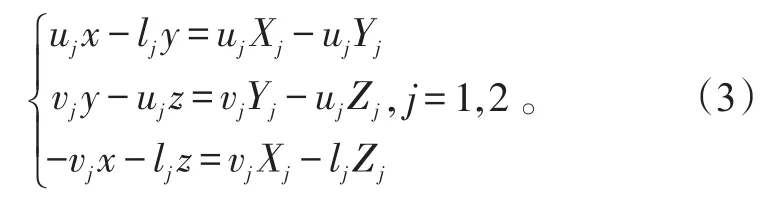
利用最小二乘法解决方程组中独立等式个数大于未知量个数的问题的方法［13］可求出目标在J2000坐标系中目标位置矢量r=（x，y，z）。

2.2仿真条件设置

首先明确定位仿真实验的输入条件，已知在某时刻4 Sep 2014 04：00：00.000（UTCG），监视卫星S1在J2000坐标系中的位置、速度矢量分别为：

另一颗与之串行编队飞行的监视星S2在J2000坐标系中的位置、速度矢量分别为：

假设星载相机的性能参数如表2所示。设定2颗监视卫星此时的姿态角和目标在CCD平面上的成像点的像素坐标如表3所示。

2.3仿真结果及结论

已知卫星的位置速度，可以求解卫星的轨道六根数［14］，对该时刻2颗监视卫星的轨道六根数进行解算。结果如表4所示。

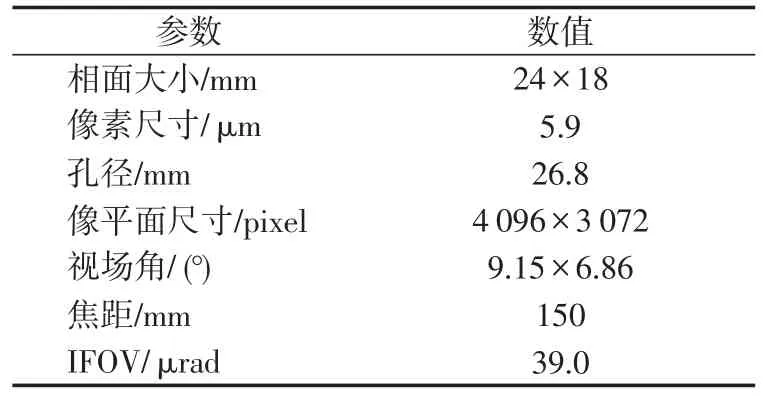
表2　星载相机性能参数Tab.2 Performance parameters of the camera on the satellite

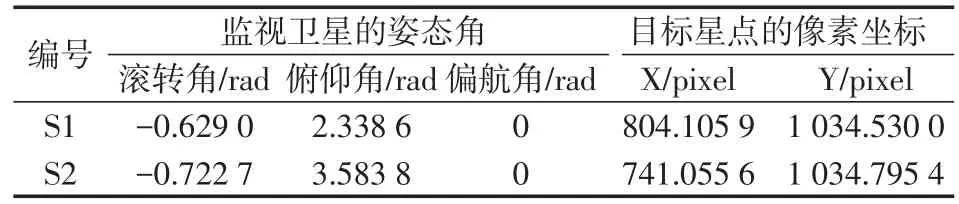
表3　监视星的姿态及目标在星图上的像素位置Tab.3 Attitude of surveillance satellites and the coordinates of the target

表4　监视卫星轨道根数的计算结果Tab.4 Results of the classical orbital elements of the surveillance satellites

从表4中可以看出，2颗监视卫星在同一轨道上飞行，真近点角前后相差4°，这与已知的2颗监视卫星串行编队飞行的信息相吻合，验证了轨道六根数求解的正确性。

已知目标星点在星图上的像素坐标和相机的焦距就可以求得目标在测量坐标系中的位置矢量，代入表3中的数据，可求得：

之后，可由转换矩阵IM求得惯性坐标系下目标相对于测量坐标系的方向矢量V=IMdm，计算结果为：

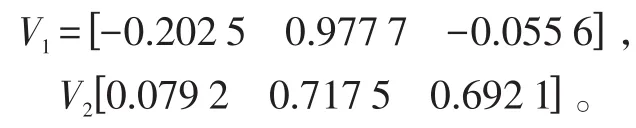
最后，代入式（4）求出目标在惯性系中的位置坐标为：

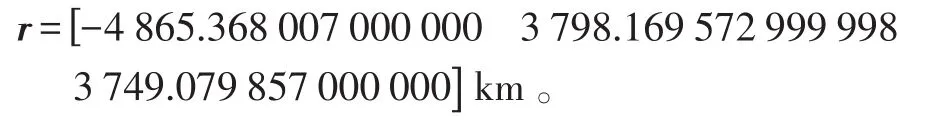
已知目标的实际位置为

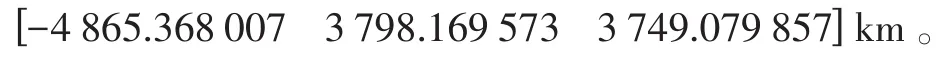
由此可知，2.1节建立起来的双星几何定位模型是可以对目标进行有效定位的，且模型误差很小，至少保证在10-5m的量级上是准确的。

3　误差分析

3.1误差仿真条件设置

以2.2节中的仿真数据为基础，按现阶段空间光学定位系统的误差选取经验值生成随机误差，将随机误差加到2.2节中的真实值上，生成带误差的输入条件，之后进行仿真计算。这里主要考虑4种误差源，即监视星的位置、速度、姿态误差以及星点的提取误差，位置误差仿真取均值为0 m，标准差为10 m的正态随机误差分别加到惯性系中位置的3个坐标分量上；速度测量误差仿真取均值为0 m/s，标准差为0.033 m/s的高斯随机误差分别加到惯性系中速度的3个坐标分量上；监视卫星的姿态误差仿真取均值为0°，标准差为24″的高斯随机误差分别加到滚转角和俯仰角上，偏航角无误差。CCD星点的提取误差在x、y方向分别取均值为0 pixel，标准差为0.33 pixel的高斯随机误差加到模拟的星点信息上。

3.2具体仿真步骤

以只加监视卫星S1的位置误差为例，对误差的计算仿真过程做出详细的说明：

按监视卫星位置的测量误差经验统计情况（每个轴方向的均值为0 m，三倍均方差为30 m）随机生成n组位置误差ΔR（i）=［Δx（i） ，Δy（i） ， Δz（i）］，i=1，2，…，n，将位置误差ΔR（i）加到真实位置R上，得到带误差的位置坐标R′（i），将R′（i）作为计算的输入量，带入模型进行计算，得到目标的位置矢量r′（i）。

记定位误差为：

Δr（i）=r′（i）-r=［Δx（i），Δy（i），Δz（i）］，i=1，2，…，n，其中，r为目标的真实位置，得到n组定位误差结果之后做统计分析。

与目标实际位置的距离误差的平均值：

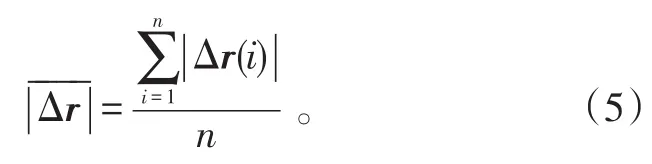
最后，对n组误差计算结果的标准差进行统计，用到的样本标准差统计：

式（6）中：xi表示。在这里，考虑计算机的计算能力且在不影响结论的前提下将n取为500。

3.3误差仿真结果及分析

表5给出了在监视星分别带有4种误差时的定位误差结果统计情况。

从表5中可以看出：监视卫星在位置误差取标准差为10 m的零均值高斯分布误差且不考虑其他误差时，定位算法的精度优于20 m（1σ）；在速度误差取标准差为0.033 m/s的零均值高斯分布误差且不考虑其他误差时，定位算法的精度优于3.5 m（1σ）；在姿态误差取标准差为24″的零均值高斯分布误差且不考虑其他误差的影响时，定位算法的精度优于95 m（1σ）；在星点提取误差取标准差为0.33 pixel的零均值高斯分布误差且不考虑其他误差时，定位算法的精度优于15 m（1σ）。

当考虑监视卫星的上述4种误差源的影响时，定位算法的精度优于100 m（1σ），当其中只有1颗监视星存在误差时，定位算法的精度优于75 m（1σ）。

表5　距离误差均值的仿真计算结果Tab.5 Simulation results of the distance-error average

表5列出了定位结果的距离误差，但在3个惯性轴方向上，求均值时正负误差存在相互抵消的情况，因而误差的大小主要体现在均方差上。为此，对4种误差源引起的3个惯性轴上的误差均方差以及距离误差的均值做柱状图进行比较，如图4所示。

图4　2颗视卫星均含有误差时定位误差统计Fig.4 Statistic of the positioning-error considering the errors of two satellites

从图4中可以看出，在上述假设的误差条件下：①监视星的姿态误差对最后定位精度的影响最大，统计结果表明，监视星姿态误差单独作用的误差影响几乎相当于总误差的0.9～0.95倍，这就表明提高监视卫星的姿态确定精度对提高模型最后的定位精度意义重大；②距离误差对定位精度的影响仅次于姿态确定误差，但大小只有姿态误差的1/4；③星点提取误差对定位精度的影响较距离误差略小，其本质与姿态误差是相同的，都属于测角误差，有时也可以将其与姿态误差放在一起进行考虑；④速度误差的影响最小，且数值上与总误差相差2个量级，做简化处理时，可不考虑其对定位精度的影响；⑤定位误差对于各个方向上来说是非均匀的，如此次仿真条件下，5种条件下Y轴方向上的定位精度都是最差的，其次是Z轴方向，而X方向定位精度最好。

3.4定位误差分布情况

首先，考虑整体定位误差的分布情况，即考虑4种误差源的影响，经过仿真计算发现误差都是围绕着某一中间值上下波动；其次，偏离中间值越大的误差出现的次数就越少。这一误差结果分布与高斯分布的特点较为吻合，文献［15］中也曾提到假设卫星姿态角、相机视线转角以及焦平面像点坐标星点提取误差服从零均值高斯分布，则空间目标的测角误差大致服从零均值高斯分布，并给出了理论推导。故选用高斯分布对误差结果进行拟合。拟合时，选取500组计算结果进行统计。

从图5、6中可以看出，在X轴方向上，误差分布与高斯分布拟合得很好；针对距离误差而言，由于不存在小于0的值，所以拟合结果稍差，但是其仍然可以用高斯分布做很好地近似。

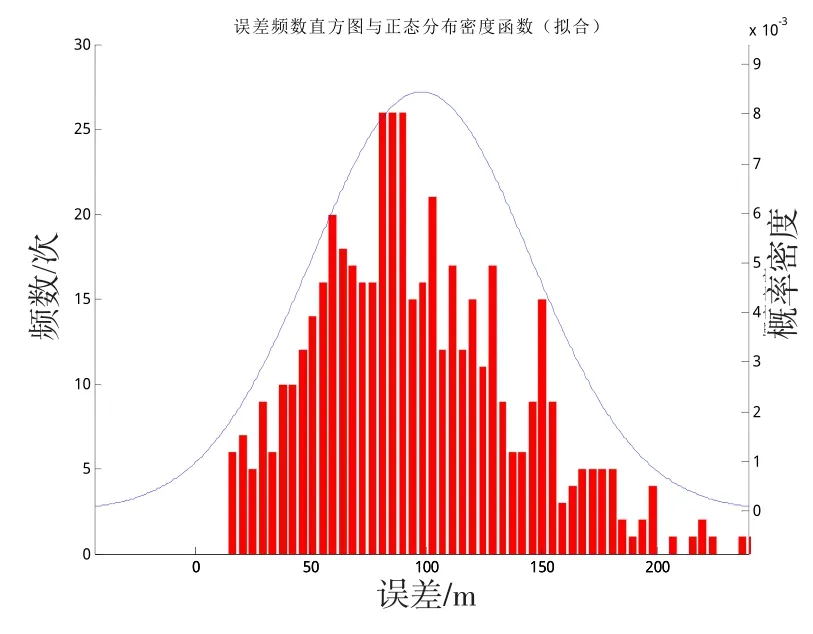
图5　考虑4种误差源时距离误差的分布Fig.5 Distribution of the distance-error when four kinds of errors in consideration

图6　考虑4种误差源时X轴方向上误差的分布Fig.6 Distribution of theX-axis-error when four kinds of errors in consideration

3.5误差源大小对定位结果的影响

上述分析计算均是基于给定均值和标准差的误差源进行的。下面考虑误差源的均值和标准差发生变化时，引起的定位误差的变化。上述计算中位置误差取均值为0 m，三倍均方差为30 m；速度测量误差取均值为0 m/s，三倍均方差为0.1 m/s；监视卫星的姿态误差取均值为0°，三倍均方差为0.02°；CCD星点的提取误差取均值为0个像素，三倍均方差为1 pixel，下面将各误差源的均方差变为原来的0.1、0.2、0.5、1、2、5、10倍，然后分别计算出定位误差，分析其随着误差源量级变化的变化情况。计算结果见图7。从图7中可以看出，双星定位模型中位置，速度，姿态、星点提取4种误差源的大小均与最终定位结果的误差近似呈线性关系。

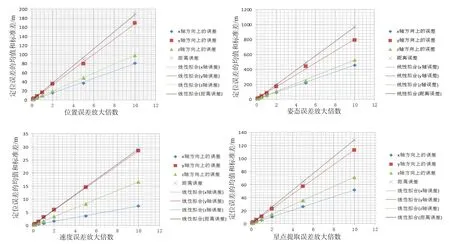
图7　定位误差随4种误差源的变化情况Fig.7 Transformation of the positioning-error when four kinds of errors change

4　结论

本文利用真实星图对星图的去噪、星点提取进行了分析，并对几种不同的星点提取算法进行了验算和比较。建立了双星几何定位模型并进行了定位算法的数学仿真验证，并结合蒙特卡洛打靶方法对定位算法进行了误差仿真实验。结果表明：使用合理的阈值对图像分割处理后，形心法对星点的提取可达到较高精度，优于考虑灰度的质心提取算法，但其提取精度严重依赖于阈值的选择；当阈值选择不合理时，各种质心提取算法的提取精度都会下降，其中阈值质心法对阈值选择的敏感性最低。因此，如可有效地确定最佳阈值，则选用形心法进行星点提取；若无法确定阈值的选择是否准确，可直接采用阈值质心算法计算。

通过分析可知：文中建立的定位算法可对目标实现较为精确的定位，当位置、速度、姿态和星点提取误差分别取标准差为10 m、0.033 m/s、24″和0.33 pixel的零均值高斯分布误差时，定位算法的精度优于100 m（1σ）；姿态误差对定位方法的精度影响最大，数值上可以达到总误差的0.9倍以上，速度误差的影响最小，只有总误差的1/30，可以忽略；定位误差近似呈高斯分布，且定位误差的大小与误差源近似呈线性关系。

［1］李冬，易东云，程洪玮.天基空间目标监视的短弧段定轨技术［J］.宇航学报，2011，32（11）：2339-2345. LI DONG，YI DONGYUN，CHENG HONGWEI.Orbit determination with short arcs for space-based space object surveillance［J］.Journal of Astronautics，2011，32（11）：2339-2345.（in Chinese）

［2］贾辉.高精度星敏感器星点提取与星图识别研究［D］.长沙：国防科技大学，2010. JIA HUI.Star centroid estimation and star identification of high accuracy star tracker［D］.Changsha：University of Defense Technology，2010.（in Chinese）

［3］陈赜.星图快速识别与定位技术研究［D］.成都：电子科技大学，2007. CHEN ZE.Research on the high-precision location and rapid recognition of star image［D］.Chengdu：University of Electronic Science and Technology，2007.（in Chinese）

［4］STONE R C.A comparison of digital centering algorithms［J］.The Astronamical Journal，1989，97（4）：1227-1237.

［5］SEITZ P.Optical super resolution using solid-state cameras and digital signal processing［J］.Optical Engineering，1988，27（7）：535-540.

［6］FILLARD J P.Sub-pixel accuracy location estimation from digital signals［J］.Optical Engineering，1992，31（11）：2465-2471.

［7］李骏.空间目标天基光学监视跟踪关键技术研究［D］.长沙：国防科技大学，2009. LI JUN.Research on key technologies of space objects surveillance and tracking in space-based optical surveillance［D］.Changsha：National University of Defense Technology，2009.（in Chinese）

［8］堪钊，华卫红.基于CCD星图的空间目标精确光学定位方法研究［D］.长沙：国防科技大学，2009. SHEN ZHAO，HUA WEIHONG.A method based on cad star image for space-object accurate optical localization［D］.Changsha：National University of Defense Technology，2009.（in Chinese）

［9］张辉，田宏，林玲，等.空间目标天基天文定位误差分析［J］.宇航学报，2010，31（5）：1345-1351. ZHANG HUI，TIAN HONG，LIN LING，et al.Error analysis of spaced-based celestial positioning for space object［J］.Journal of Astronautics，2010，31（5）：1345-1351.（in Chinese）

［10］王秀红，李俊峰，王彦荣.天基照相机监测空间目标定轨方法及精度分析［J］.光学精密工程，2013，21（6）：1394-1403. WANG XIUHONG，LI JUNFENG，WANG YANRONG. Orbit determination and precision analysis of space object with space-based camera［J］.Optics and Precision Engineering，2013，21（6）：1394-1403.（in Chinese）

［11］刘美莹，王虎，汶德胜，等.空间目标天文定位方法及观测分析［J］.光子学报，2014，43（11）：159-166. LIU MEIYING，WANG HU，WEN DESHENG，et al.Celestial positioning method and observation analysis for space object［J］.Acta Photonica Sinica，2014，43（11）：159-166.（in Chinese）

［12］王兆魁，张育林.一种CCD星图星点快速定位算法［J］.空间科学学报，2006，26（3）：209-214. WANG ZHAOKUI，ZHANG YULIN.Algorithm for CCD Star Image Rapid Locating［J］.Chinese Journal of Space Science，2006，26（3）：209-214.（in Chinese）

［13］邹乐强.最小二乘法原理及其简单应用［J］.科技信息，2010（23）：282-283. ZOU LEQIANG.The theory and simple application of least squares method［J］.Science and Technology Information，2010（23）：282-283.（in Chinese）

［14］杨嘉樨，吕振铎.航天器轨道动力学与控制［M］.北京：中国宇航出版社，2002：56-57. YANG JIAXI，LV ZHENDUO.Spacecraft orbit dynamics and control［M］.Beijing：China Aerospace Press，2002：56-57.（in Chinese）

［15］张萍，易东云，吴诩，等.空间预警系统的视线测量误差特性研究［J］.中国空间科学技术，2004，12（6）：48-53. ZHANG PING，YI DONGYUN，WU YI，et al.The LOS measurement error character research of space early warning system［J］.China Space Science and Technology，2004，12（6）：48-53.（in Chinese）

Method of Space Target Optical Detection and Positioning Based on Micro Satellite

GAO Yudong，CUI Kaikai
（School of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China）

To achieve space-based optical surveillance，bi-satellite geometric positioning model was established.According the binary geometric positioning theory，with angular-measure-only principle，the position of the target was obtained by using least square method.Because the result of star chart processing would directly affect the final positioning accuracy，the grey scale characteristic was analyzed.Comparing several different star point extraction algorithms by using real chart，some extraction algorithms were validated and compared and two feasible point extraction algorithms were found out. The bi-satellite geometric positioning model was simulated.The algorithm positioning error was combined by using Monte Carlo method.The conclusions showed that the positioning error was less than 10-5m without error source.And the positioning error was less than 100m when taking four main error sources into consideration and the attitude measurement error gave the greatest impact on the precision of positioning method.And the positioning error was approximately normal distribution and almost liner with error sources.So this positioning algorithm could locate the target with high accuracy.The result of this paper has the value of engineering application.

star point extraction；bi-satellite positioning；Monte Carlo method；positioning error

V448.2

A

1673-1522（2016）03-0365-07DOI:10.7682/j.issn.1673-1522.2016.03.012

2015-08-20；

2016-04-23

国家863计划支持基金资助项目（2015AAXXXX23G）

高玉东（1979-），男，副研究员，博士。