多层倾斜介质转换波地震正演方法研究

白　超

(西北大学地质学系/国家大陆动力学重点实验室，陕西 西安 710069)



多层倾斜介质转换波地震正演方法研究

白超

(西北大学地质学系/国家大陆动力学重点实验室，陕西 西安 710069)

转换波射线追踪正演对于转换波的理论研究、转换波资料处理、转换波资料解释和转换波野外施工设计都是一个重要的工具。阐述多层倾斜界面情况下，转换波射线追踪的基本原理、实现方法和利用此方法算出的三个模型的正演实例。以多层介质转换波观测系统为基础，设计的正演模型主要有：(1)一层倾斜介质模型；(2)两层倾斜介质模型；(3)三层倾斜介质模型。采用试射法为主要正演方法，对上述三种模型进行正演。最终得出模型图、射线路径图和地震响应图等图件，得出每一层的上行波和下行波，验证算法的有效性。

转换波；地质模型；射线追踪；试射法；多层介质

多波多分量地震勘探是地震学界近年来取得的最为重要的研究成果，而转换波技术是进一步提高地震勘探精度的重要工具，与相对单一的纵波勘探相比，转换波数据提供更为丰富的岩性物性信息，这些信息在地下岩性、物性判断等方面发挥重要作用。因此，转换波技术倍受关注[1][2]。

目前转换波计算公式是在单层介质下推倒出来的，相对比较单一，而在多层倾斜介质模型中推到出来的共转换点技术，跟实际的地质情况比较接近，对实际更有指导意义，应用效果明显优前者[3]。

1　转换波产生原理

P波(纵波):波的传播方向与质点的震动方向一致。

S波(横波):波的传播方向与质点的震动方向垂直。

转换波:震源产生的下行纵波以某一角度入射，遇到界面后转换为横波,上行横波传播至地面,这时的上行的横波不是由震源产生,而是由入射纵波转换得到,称为转换波[4][5]。下行纵波与上行横波不对称。反射原理见图1。

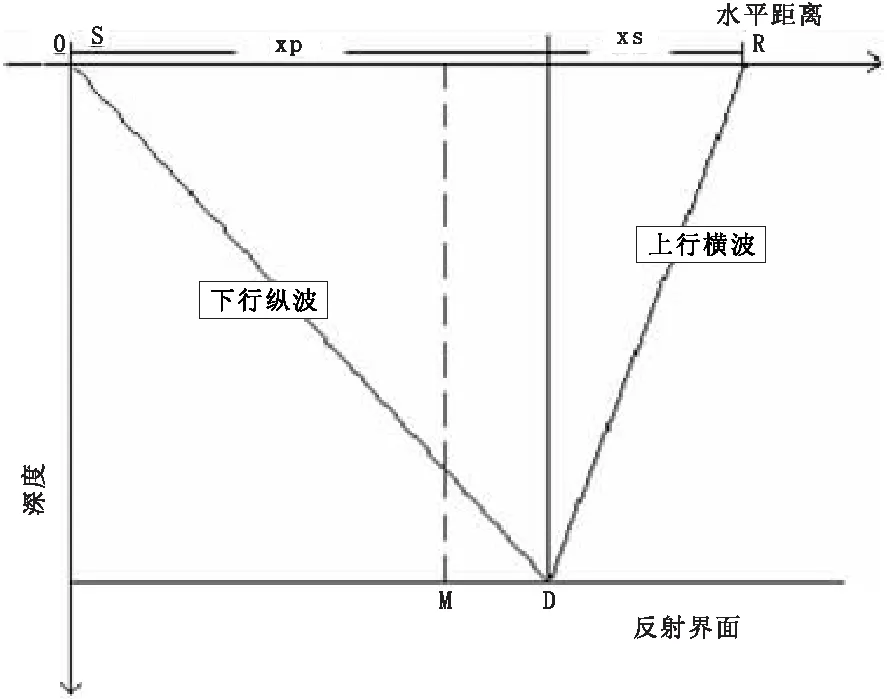
图1　转换波的产生

1.1转换点位置计算

转换波在传播过程中下行波是纵波，上行波是横波，它的入射和反射的射线路径是不对称的，转换点即反射点，它不在炮点和检波点的中心上，而是靠近检波点的一面。转换波资料的处理，不能应用纵波的共中心点(CMP)叠加剖面，转换波的叠加剖面应为共反射点(即共转换点)叠加，而不是共中心点叠加。PS转换波处理中共转换点(CCP)道集抽取及叠加是很关键的处理步骤[6]。

1.2转换波主要特点及处理关键

(1)换波穿透能力强；(2)纯横波相比，转换波具有高信噪比，宽频带、短记录等特点；(3)转换波的菲涅尔带通常比纵波小，因此有较高的空间分辨率(尤其是横向分辨率)；(4)转换波不对称，且时距曲线不是双曲线；(5)采用试射法，研究出适用于转换波的射线追踪基本流程，并编制了转换波的射线追踪计算机程序；(6)采用试射法对倾斜(单层、多层)地层理论模型的进行了转换波射线追踪模拟计算，利用射线追踪算法模拟转换波的合成地震记录[7]。

2　射线追踪原理及方法

2.1试射法原理

即以一个初始入射角度入射，求其射线路径。一般情况下，此射线不能到达预定的接收点，需根据实际到达点和预定接收点之间的偏差，通过修改初始入射角度，再次追踪射线路径,直至射线实际到达位置和预定接收位置在一定误差范围之内[8]。

应用试射法原理进行正演模拟，主要是根据已知设计的地质模型和观测系统，追踪出射线路径并计算其地震响应，其主要特点如下：

(1)追踪到的波既包括反射波和透射波。

(2)地质模型界面可以倾斜。

(3)本方法也适用于大偏移距的情况。

利用试射法进行射线追踪，采用如下的思想进行判断[9]。

入射角α以0°为起始角，Δa=1°为增量进行试射，并求出每一试射角射线与观测点所在直线的交点坐标(x,z)。ε为误差范围。

若︱z-zr∣≤ε，则α即为所求入射角，否则：

若︱z-zr∣>ε，且z>zr，则令α=α-Δa/2

若︱z-zr∣﹥,且z﹤zr，则令α=α+Δa/2

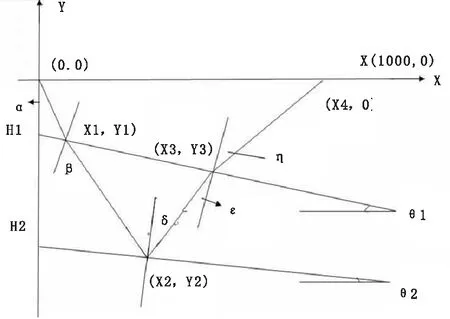
多层倾斜介质如图2所示，炮点S，检波点R，炮检距X，射线从S传播到R的旅行时t，设共有n层，则：

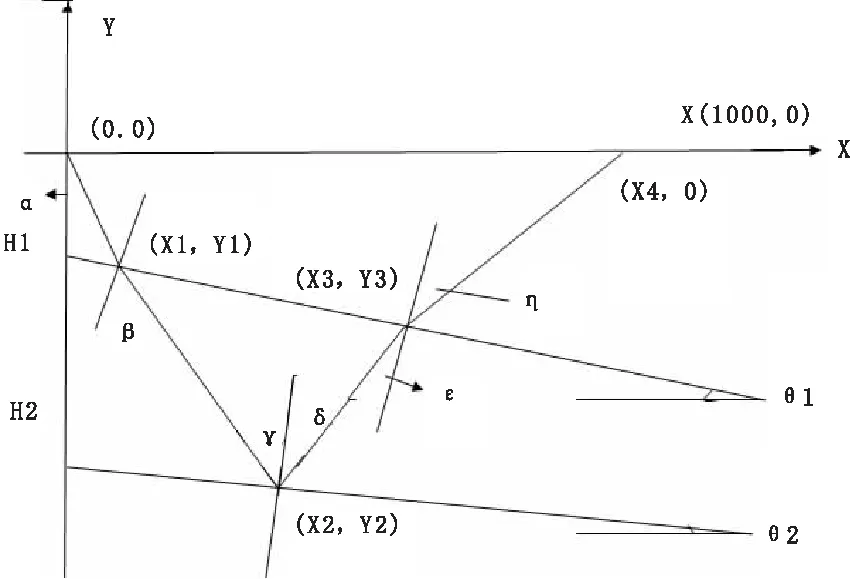
图2　层状介质示意图

(1)

根据Snell定律有：

(2)

其中αi为射线在各界面的入射角，Vi为各层的速度(i=1，2，…，n)

将式(2)代入式(1)有：

X=X1+X2+X3+X4=H1/(cotα-tanθ1)+ {cot(β-θ1)×[X1-tan(β-θ1)× Y1]+H2}/[cot(β-θ1)-tanθ2]+ [tan(Pi/2-γ-δ+β-θ1)-H2-Y1]/[tan(Pi/2-γ-δ+β-θ2)+tanθ2]+ tan(Pi/2-θ1-θ2)×X3-Y3/tan(Pi/2-θ1-θ2)；

t=sqrt(X12+Y12)/Vp1+sqrt[(X2-X1)2+(Y2-Y1)2]/Vp2+sqrt[(X3-X2)2+(Y3-Y2)2]/Vs2+ sqrt[(X4-X3)2+Y32]/Vs1；

(3)

其中为各层的厚度，采用试射法求得反射波旅行时t：

(1)入射角α1以0°为起始角，1°为增量进行试射，并求出每一试射角射线经过的距离。

(2)α增加到n度时，射线经过的倾斜距离为x2，α=m-1度时，射线经过的倾斜距离为x1，有(为炮检距)，停止增加角度试射。

(3)引进二分法进行判断：

b.如果|X-X4|<ε，则α即为所求入射角，否则

如果|X-X4|>ε且x>x0，则令α1=α1，α2=α

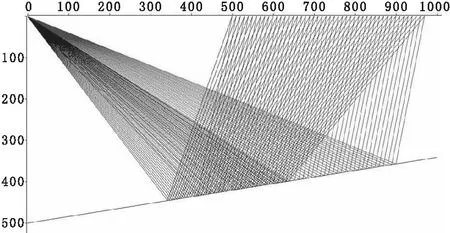
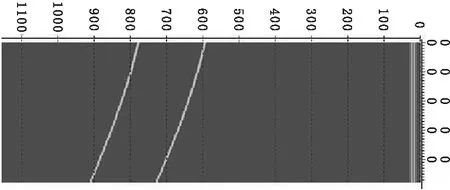
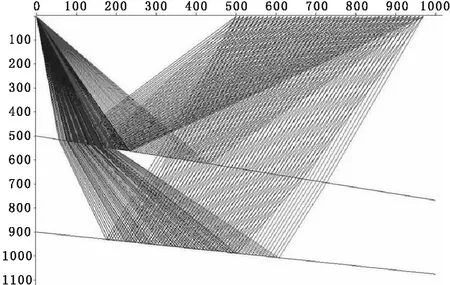
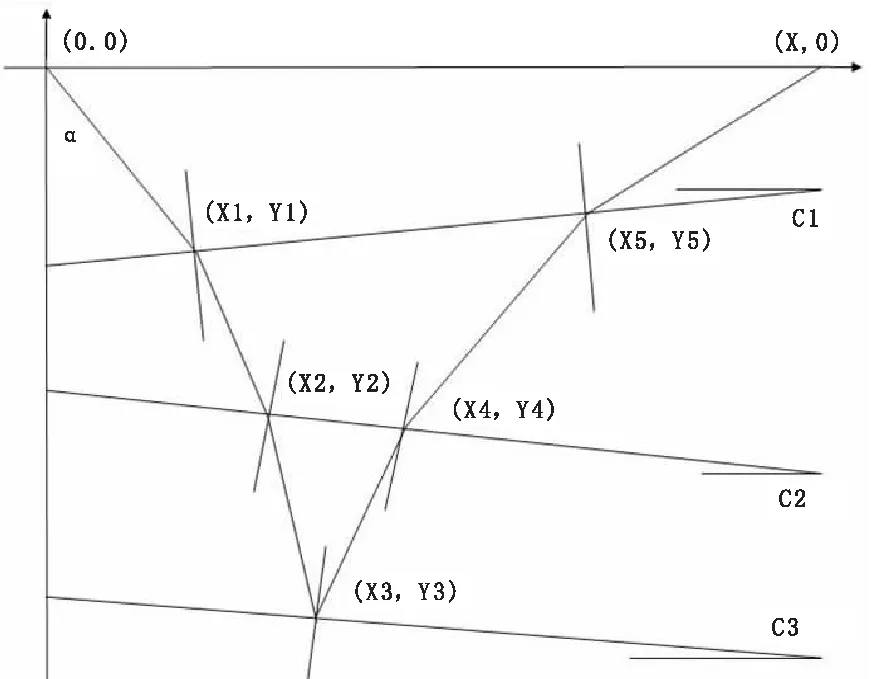
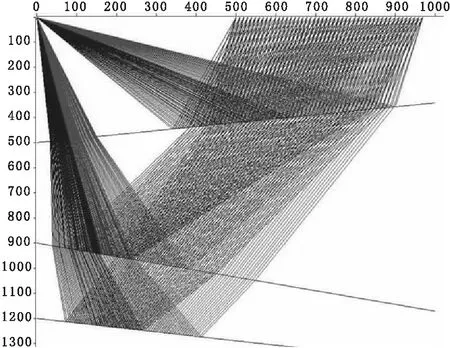
如果|X-X4|>ε且x

(4)转到(3)不断迭代，快速找到满足条件的入射角，求得射线参数，根据(3)式就可求得射线从炮点经目的层反射到检波点的旅行时t。

利用上述原理，可以快速追踪图2所示的倾斜反射界面目的层反射波。

设共有n个反射界面，各界面与地面的交点已知，第n个界面为目的反射层，已知炮点坐标(XS，ZS)和检波点坐标(XR，ZR)。

Vi为各层的层速度；αi为射线在各界面的入射角；Zi为各界面的深度；hi为各层的厚度(i=1，…，n)[10]。

2.2转换波正演模拟

首先通过模型图，建立几何坐标系，根据试射法理论，利用平面解析几何知识求出入射射线、反射射线、透射射线的方程以及它们与界面的交点，就可求得波的传播路径。计算出反射界面参数，合成地震记录。

3　转换波地震响应

文中建立的地质模型充分考虑了实际的地质情况，尽量使建立的模型符合实际情况。对多层介质结构模型进行转换波正演模拟，研究多层介质转换波的射线路经和时距曲线特征，对认识多层倾斜介质波的传播规律具有重要意义。在综合考虑了各种情况后，选取具有代表性的地质形态，建立了如下文所述的几种模型,并对这几种模型进行了分析对比。

3.1单层倾斜介质模型及其响应

图3(a)　一层倾斜界面地层模型图

图3(b)　一层倾斜界面射线路径图

图3(c)　一层介质复合地震响应图

左边为转换波地震响应，右边处为纵波地震响应，从图3(a)～图3(c)中可以看出转换波的斜率大，纵波的斜率小，这是因为转换波的波速小所致。

3.2两层倾斜介质模型及其响应

图4(a)　一层倾斜界面地层模型图

图4(b)　两层倾斜界面射线路径图

图4(c)　两层介质复合地震响应图

图4(c)为图4(b)模型的地震响应图，震源子波为Rick子波,主频50 Hz。偏移距500 m，样点数为1 200个，地震道数为48道。图中转换波地震响应和纵波反射地震响应交叉出现。

图4(c)中用(1)(2)标出的是纵波反射的地震响应，用1和2标出的是转换波的地震响应。由图4(c)可以看出，从第一层到第二层纵波反射和转换波同相轴的弯曲度逐渐变小，即纵波反射和转换波同相轴的斜率逐渐变小，即地层速度逐渐加大。纵波反射和转换波的同相轴连续性较好，这与模型中介质均匀各向同性且速度变化不大的假设相一致。纵波反射的时距曲线是双曲线，而转换波的时距曲线是近似双曲线的。

由图4(c)分析可知，转换波响应总是滞后于纵波反射地震响应，炮检距越大，转换波和纵波反射时差越大，从第一层到第二层，随地层深度增加，相同层位的转换波和纵波反射时差越来越大。

3.3三层倾斜介质模型及其地震响应

图中用(1)(2)(3)标出的是纵波反射的地震响应，用 (4)(5)(6)标出的是转换波的地震响应。由图5(c)可以看出，从第一层到第三层纵波反射和转换波同相轴的弯曲度逐渐变小，即纵波反射和转换波同相轴的斜率逐渐变小，即地层速度逐渐加大。纵波反射和转换波的同相轴连续性较好，这与模型中介质均匀各向同性且速度变化不大的假设相一致。纵波反射的时距曲线是双曲线，而转换波的时距曲线是近似双曲线的。

图5(a)　三层倾斜界面地层模型图

图5(b)　三层倾斜介质复合路径图

图5(c)　三层介质复合地震响应图

由图5(c)分析可知，转换波响应不总是滞后于纵波反射地震响应，例如第二和第三层的反射波到达时间就小于第一层的转换波的旅行时。炮检距越大，转换波和纵波反射时差越大，从第一层到第三层，随地层深度增加，相同层位的转换波和纵波反射时差越来越大。

4　结语

依据射线追踪原理，运用试射法进行多层倾斜介质转换波正演模拟。针对转换波观测系统和地震波的特征设计模型、编写程序，分别算出各个界面的路程和旅行时。通过对图件的分析，得出的结论都与理论知识相一致，从而证明了程序的算法正确、适用性良好。

(1)正演计算中，核心是使每个检波器接收到误差范围内的反射射线和透射射线；如何利用试射法使震源发出的射线(代表地震波)逼近检波点，是控制程序循环的关键。

(2)本文做了下面3个假设：①各层中地震射线为直线，误差范围为±0.5 m；②假定地层密度不变ρ1=ρ2=2，即反射系数为速度的函数；③建立模型时假定各地层都是均匀各向同性的。这三个假设是论文的基础，但是这些假设与实际的野外地质情况相差较大，如果假设能够更接近实际地质情况，正演的结果将会更具参考价值。

(3)文中的射线追踪方法只考虑了地震波的运动学特征和几何特征，即只考虑了波的传播路径，进而计算了波沿射线路径传播的路程和旅行时。主要优点是：概念清晰、运算简单并且适应性强，不足之处是应用有一定的限制。

(4)对于倾斜介质，转换波的时距曲线不是双曲线形的，炮检距越大,转换波和纵波反射的时差越大,多层倾斜介质第二反射层的时距曲线比第一个反射层的时距曲线弯曲程度小。

(5)在地震勘探中，转换波可用于确定地层速度，用于确定地层形态；通过文中的射线路径的正演可以得出探测范围，通过对转换波的分析可得出反射界面及地层的一些基本信息。

[1]李振春，张军华.地震数据处理方法[M].东营：中国石油大学出版社.2004:23-61.

[2]Richard S Lu,Dennis E Willen,lan A Watson.Identifying,removing,andimaging P-S conversions at salt-sediment interfaces[J].Geophysics,2003,68(3):1052-1059.

[3]张钋,刘洪,李幼铭.射线追踪方法的发展现状[J].地球物理学进展.2000,15(1):36-45.

[4]Gaiser James,Moldoveanu Nick.Multicomponent technology:the Players,problems,applications,and trends[J].The Leading Edge,2001,20(9):974-977.

[5]Stuart Crampin.Anisotropy in exploration seismics[J].FirstBreak,1984,2(3):19-21.

[6]李国发,彭苏萍,何兵寿,等.转换波地震资料处理的关键问题与解决方法[J].中国矿业大学学报.2005.34(1):41-45.

[7]刘清林.地震初至波射线路径的追踪[J].石油物探.1993.32(2)：5-10．

[8]张钋,刘洪,李幼铭.射线追踪方法的发展现状[J].地球物理学进展.2000,15(1):36-45.

[9]许士勇,马在田.快速有效的转换波共转换点叠加技术[J].地球物理学报.2002,45(4):557-568.

[10]朱海波.射线正演研究和采集参数的设计[D].成都：成都理工大学.2004：12-43.

2016-03-14

白超(1988-)，男，陕西渭南人，在读硕士研究生，主攻方向：石油与天然气工程。

P542+.3

A

1004-1184(2016)05-0192-04