高速铁路列车运行图结构优化研究

（1.西南交通大学交通运输与物流学院，四川成都610031；2.全国铁路列车运行图编制研发培训中心，四川成都610031）

（1.西南交通大学交通运输与物流学院，四川成都610031；2.全国铁路列车运行图编制研发培训中心，四川成都610031）

为提高高速铁路列车运行图的通过能力，通过紧凑铺画列车运行图，合理安排列车运行线顺序，优化了列车运行图结构；将列车运行图结构优化问题转化为旅行商问题，以巡回路径总费用最小化为目标建立0-1整数规划模型，并利用遗传算法求解.用2015年京沪高速铁路数据进行实例验证，求得列车运行图结构的优化方案.计算结果表明：原方案开行39列列车最少需628 min，优化方案的开行时间比原方案的开行时间减少了133 min，约21.2%，能更好地满足客流高峰时段或突发性客流激增时需尽快密集发车的要求.

铁路运输；列车运行图；遗传算法；高速铁路；通过能力；旅行商问题

我国高速铁路网正在大规模和高速度建设中，截至2014年底，总营业里程已经超过1.6万km.高速铁路运营组织是高速铁路安全平稳运行、满足旅客需求、确保铁路经济效益和社会效益的重要保障，高速铁路列车运行图是运营组织工作的基础.

国内外学者对列车运行图编制做了大量的研究，建立了丰富的数学理论和计算方法，这些成果对编制高速铁路列车运行图具有重大的借鉴意义.文献［1-8］对既有铁路单线、双线和网状线路的列车运行图进行了深入的研究；文献［9］系统地研究了基于网状线路的京沪高速铁路列车运行图编制理论，设计了高中速列车分层始发区域滚动铺画算法对运行图数学模型进行求解；文献［10］提出基于不同种类列车运行图铺划的分层叠加数学模型，设计了改进型遗传算法对其进行求解；文献［11-12］对周期性列车运行图进行优化，通过铺画某线路的周期性列车运行图验证了模型的可行性；文献［13-14］在考虑旅客列车始发时间域和维修天窗的基础上，建立了客运专线列车运行图优化模型，设计了基于定序优化的客运专线列车运行图铺画方法，并基于旅客列车开行方案和列车运行图的换乘网络进行客流分配，将旅客列车开行方案和列车运行图相结合进行了优化.

在既定高速铁路停站方案的前提下，列车运行图结构在很大程度上影响铁路的通过能力.紧凑铺画列车运行图，合理布线进而优化其结构，可以提高铁路通过能力，有利于满足客流高峰时段或突发性客流激增情况下尽快密集发车的需求.本文将高速铁路列车运行图的结构优化问题转化为旅行商问题（traveling salesman problem，TSP），建立数学模型并用遗传算法［15］求解.以京沪高速铁路为实例，编制出优化的列车运行图方案.

1 高速铁路列车运行图数学描述

｛xi1，xi2，…，xin｝表示列车Ti的停站序列.tj表示高速列车在站Sj的停站时分，tZC表示不停站直达列车的旅行时分，tQF表示起车附加时分，tTF表示停车附加时分.

定义1 对任意两列车Ti1和Ti2，当Ti2为Ti1的紧后行列车时，找不到比Δti1i2更小的始发站发车间隔时间，使得这两列车在任意车站均满足相应的车站间隔时间，称Δti1i2为列车Ti1和Ti2的最小始发间隔时间.

根据高速铁路已定的停站方案，由列车运行标尺、起车和停车附加时分、停站时分等已知参数，可以计算出任意两列车Ti1和Ti2的最小始发间隔时间Δti1i2，具体方法参照文献［10］.

定义2 列车运行图中的任意两条相邻列车运行线在始发站的间隔时间等于这两列车的最小始发间隔时间，这种铺画方式称为紧凑铺画.

2 高速铁路列车运行图建模

根据既定的高速铁路停站方案，通过对列车进行合理排序，优化列车运行图结构，可以提高铁路通过能力.优化目标为使紧凑铺画的列车运行图中第一列列车从始发站出发至最后一列列车到达终到站之间的总间隔时间最短.

将每条列车运行线视为一个节点，构造节点网络完全图.用k表示节点编号（与其对应的运行线编号）.令从节点k1指向节点k2的路径的费用等于列车Ti1和Ti2的最小始发间隔时间，那么根据定义1和定义2，整个网络完全图中所有路径的费用可以根据既定的高速铁路停站方案来确定.

由于优化目标还涉及到运行线的运行时分，而这部分内容并没有在节点网络完全图中得以体现，这将导致在后续的建立模型和求解过程中陷入困境.

为便于研究，增设一个虚拟节点，编号为m+ 1.令之前的m个节点到节点m+1的路径费用等于各列车运行线的运行时分，设节点m+1到其他各节点的路径费用为0，由此形成扩展的节点网络完全图.

在新的节点网络完全图中，从任一节点出发，遍历所有节点1次并回到该节点，该巡回路径的拓扑结构是一个环.若将该环在节点m+1处断开并去掉节点m+1，将形成一条链，这时可以确定各节点的顺序.按照此顺序紧凑铺画各节点对应的列车运行线，所有相邻列车运行线的间隔时间与最末一条运行线的运行时分之和正好等于该巡回路线的总费用.也就是说，为了优化列车运行线顺序，使得相邻列车运行线的各间隔时间与最末一条运行线的运行时分之和最小，即在节点网络完全图中寻找总费用最小的巡回路径.

由构造的节点网络完全图寻找最优巡回路径 的过程如图1所示，优化结果的节点顺序为3241.

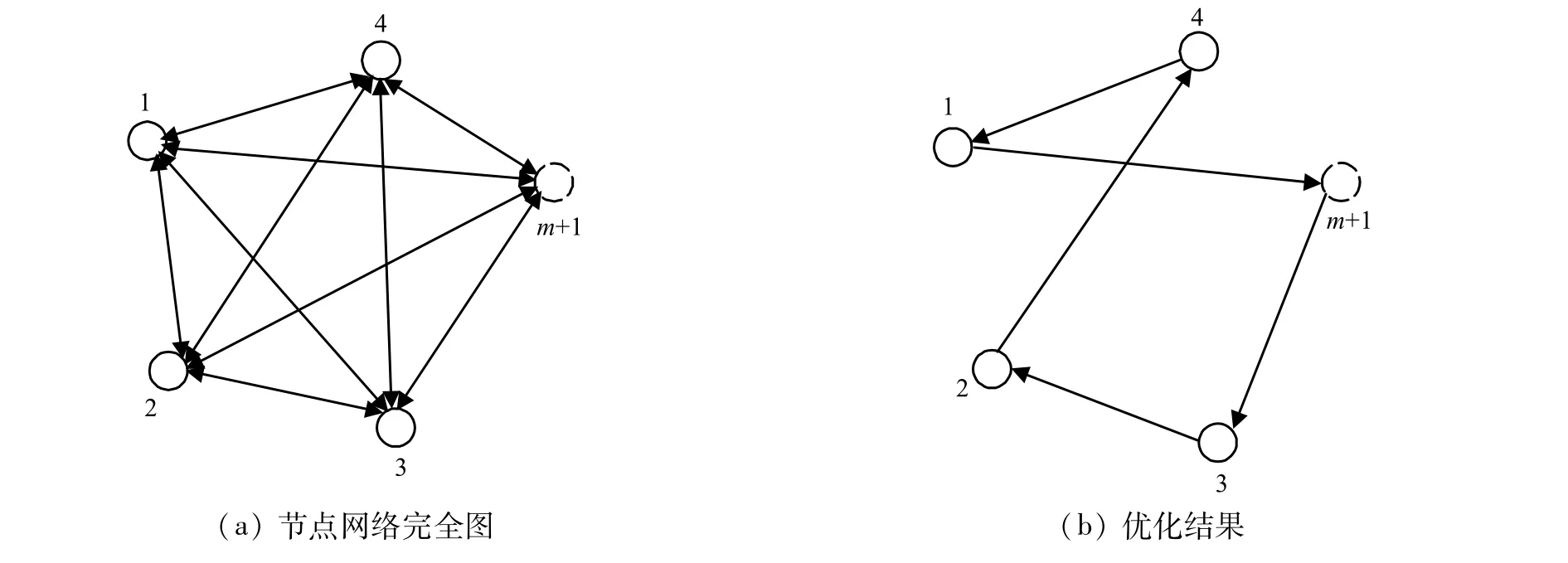
图1 优化过程Fig.1 Optimization process

紧凑铺画时列车运行图结构的优化问题可转化为经典的旅行商问题（TSP）.设G=（V，E）是带正权的完全图，V=（1，2，…，m+1），E表示完全图中所有边的集合，边（k1，k2）的费用记为Ck1k2.

节点网络完全图的费用矩阵

用变量λk1k2表示边（k1，k2）是否存在于总费用最小的巡回路径中，若是λk1k2=1，否则λk1k2=0.这里有一种特殊情况，若k1=k2时，取λk1k2=0，因为这样的边在节点网络完全图中并不存在.所以待求解的矩阵

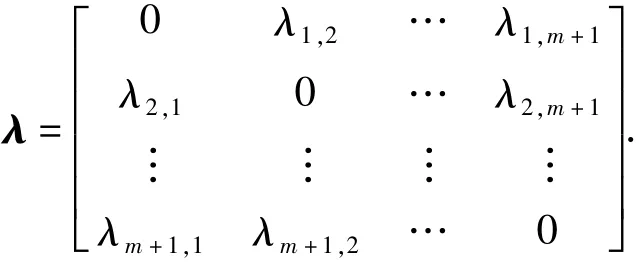
为了优化紧凑铺画列车运行图的结构，确定最优的列车运行线顺序，实现第一列车从始发站出发至最末列车到达终到站的间隔时间最小化的目标，巡回路径总费用最小化的TSP问题表达为

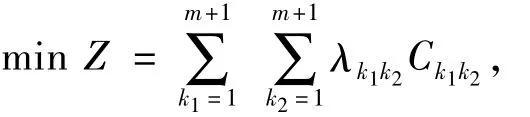
式（1）和式（2）表示任一节点在巡回路径中只能出现一次，式（3）表示巡回路径必须遍历所有节点.

3 遗传算法参数设计

3.1 染色体编码

采用以遍历节点的次序进行编码的方法，如码串123456表示从节点1开始，依次经节点2、3、4、5和6，最后返回节点1的遍历路径，这是针对TSP问题的最自然的编码方式.

3.2 适应度函数

适应度函数常取路径长度Td的倒数，即f= 1/Td.结合TSP的约束条件（每个节点经过且只经过一次），适应度函数修正为

f=1/（Td+αNt），

式中：Nt为对TSP路径不合法的度量，这里取Nt为未遍历的节点的个数；

α为惩罚系数，取值通常为节点之间最长距离dmax的两倍多，这里取2.1dmax；

3.3 遗传算子

（1）选择算子

用适应度函数对群体中所有个体进行评估，将选择算子作用于群体，选择的目的是把优化的个体直接遗传到下一代，或通过配对交叉产生新的个体再遗传到下一代.采用轮盘赌与精英个体保存的混合策略，选择当前种群中的最优个体直接进入下一代，剩余个体通过轮盘赌随机选择，这种方式能够在一定程度上避免算法过早收敛.

（2）交叉算子

采用部分匹配交叉策略：随机选择两个交叉点，将两交叉点之间的基因段互换，将互换后的基因段以外的部分中与互换后基因段中冲突的节点用另一父代相应位置的码值代替，直至没有冲突.

（3）变异算子

对群体中的个体，随机选择染色体中的两点，交换其码值.

3.4 遗传算法求解流程

具体步骤如下：

（1）设定参数，种群大小为Mpop，交叉概率为Pc，变异概率为Pm，最大遗传代数为nmax.

（2）按照染色体编码方式生成初始种群，当前代数n=1.

（3）计算当前种群中各染色体的适应度，选择最优个体直接进入下一代，剩余个体通过轮盘赌随机选择.

（4）根据给定的交叉概率Pc，对种群进行一致性交叉操作.

（5）根据给定的变异概率Pm，对种群进行变异操作，更新代数n=n+1.

（6）算法终止条件.若n≤nmax，转步骤（3）；否则，输出当前种群中最优染色体，并解码为列车运行图编制方案.

4 实例验证与结果分析

为检验算法效果，用2015年京沪高铁为例进行验证.以全路运行图中由北京南始发上海虹桥终到的全部39列速度为300 km/h的下行列车为研究对象.

tZC=276 min，

tQF=2 min，

tTF=3 min.

全路运行图中京沪高铁在各站的停站时间如表1所示，具体停站方案如表2所示.

表1 京沪高铁各站停站时间Tab.1 Train stop time of Beijing-Shanghai high-speed railway min

全路运行图中各列车的铺画顺序为：G101、G103、G105、G11、G107、G109、G111、G1、G113、G115、G117、G13、G119、G121、G15、G123、G125、G411、G127、G129、G131、G133、G135、G137、G3、G139、G141、G17、G143、G145、G19、G147、G149、G151、G21、G153、G155、G157、G159.若这些运行线紧凑铺画，总用时628 min.

将表2中各列车依次编码为1至39，增加一个虚拟节点，其编号为40.设定遗传算法参数，种群大小

Mpop=60，

交叉概率

Pc=0.4，

变异概率

Pm=0.05，

最大遗传代数nmax=300.

经300次迭代后，取当代种群中最优染色体，其编码为1-2-5-6-4-3-7-15-13-38-9-8-18-26-24-14-31-35-37-10-22-36-25-16-12-20-32-33-30-17-39-19-34-27-21-11-28-23-29-40，去除最末的虚拟节点，解码成列车运行线的铺画顺序：G1、G3、G15、G17、G13、G11、G19、G113、G109、G159、G101、G21、G119、G135、G131、G111、G145、G153、G157、G103、G127、G155、G133、G115、G107、G123、G147、G149、G143、G117、G411、G121、G151、G137、G125、G105、G139、G129、G141，总用时495 min，比现行方案缩短133 min，约21.2%，大幅度地提高了列车运行图的通过能力.

表2 京沪高铁停站方案Tab.2 Stop schedule plan of Beijing-Shanghai high-speed railway

5 结 论

本文从紧凑铺画列车运行图力求通过能力最大为出发点，建立了高速铁路列车运行图结构优化数学模型，并设计了遗传算法参数进行求解.以2015年京沪高铁为例，编制出结构更合理的列车运行图方案，得到以下主要结论：

（1）通过实例计算，确定了更合理的运行线顺序.优化方案总用时比现行方案缩短了133 min，优化方案有重要的现实意义，可以较好地满足客流高峰时段或突发性客流激增时需尽快密集发车的需求.

（2）以2015年京沪高铁高速列车为研究对象，是基于不存在越行情况，若不同速度的高速列车没有越行现象，本文方法同样适用.

对于我国逐渐成型的高速铁路网络，条件更加复杂，列车运行图的结构还需进一步深入研究.

［1］ 彭其渊，王慈光.铁路行车组织［M］.北京：中国铁道出版社，2007：266-275.

［2］ 孙焰.单线列车运行图优化理论及计算机编制方法［D］.长沙：长沙铁道学院，1997.

［3］ 周磊山，胡思继.计算机编制网状线路列车运行图方法研究［J］.铁道学报，1998，20（5）：15-21.

ZHOU Leishan，HU Siji.Network hierarchy parallel algorithm of automatic train scheduling［J］.Journal of the China Railway Society，1998，20（5）：15-21.

［4］ 倪少权，吕红霞，杨明伦.全路列车运行图编制系统设计的研究［J］.西南交通大学学报，2003，38（3）：332-335.

NI Shaoquan，LV Hongxia，YANG Minglun.Research on design of train diagram-making system of railways in China［J］.Journal of Southwest Jiaotong University，2003，38（3）：332-335.

［5］ 彭其渊，杨明伦，倪少权.单线实用货物列车运行图计算机编制系统［J］.西南交通大学学报，1995，30（5）：537-542.

PENG Qiyuan，YANG Minglun，NI Shaoquan.A system of making train working graph on single-track lines with computer［J］.Journal of Southwest Jiaotong University，1995，30（5）：537-542.

［6］ 彭其渊，朱松年.网络列车运行图的数学模型及算法研究［J］.铁道学报，2001，23（1）：1-8.

PENG Qiyuan，ZHU Songnian.Study on a general optimization model and its solution for railway network train-diagram［J］. Journal of the China Railway Society，2001，23（1）：1-8.

［7］ 史峰，黎新华，秦进，等.单线列车运行图铺划的时间循环迭代优化方法［J］.铁道学报，2005，27（1）：1-5.

SHI Feng，LI Xinhua，QIN Jin，et al.A timing-cycle iterative optimizing method for drawing single-track railway train diagrams［J］.Journal of the China Railway Society，2005，27（1）：1-5.

［8］ 史峰，黎新华，秦进，等.单线列车运行调整的最早冲突优化方法［J］.中国铁道科学，2005，26（1）：106-113.

SHI Feng，LI Xinhua，QIN Jin，et al.The earliest conflict optimal method for train operation adjustment on single track［J］. China Railway Science， 2005，26（1）：106-113.

［9］ 马建军.基于网状线路的京沪高速铁路列车运行图编制理论的研究［D］.北京：北方交通大学，2002.

［10］ 许红，马建军，龙建成.客运专线列车运行图编制模型及计算方法研究［J］.铁道学报.2007，29（2）：1-7.

XU Hong，MA Jianjun，LONG Jiancheng.Research on the model and algorithm of the train working diagram of dedicated Passenger line［J］.Journal of the China Railway Society，2007，29（2）：1-7.

［11］ 谢美全，聂磊.周期性列车运行图优化模型研究［J］.铁道学报，2009，31（4）：7-13.

XIE Meiquan，NIE Lei. Modelofcyclic train timetable［J］.Journal of the China Railway Society，2009，31（4）：7-13.

［12］ 汪波，杨浩，牛丰，等.周期运行图编制模型与算法研究［J］.铁道学报，2007，29（5）：1-6.

WANG Bo，YANG Hao，NIU Feng，et al.Study on modeland algorithm of periodic train diagram generation［J］.Journal of the China Railway Society，2007，29（5）：1-6.

［13］ 周文梁，史峰，陈彦.基于定序优化的客运专线列车运行图铺划方法［J］.铁道学报，2010，32（1）：1-7.

ZHOU Wenliang，SHI Feng，CHEN Yan.A method for drawing train diagram of deticated passenger line based on fixed order optimization［J］.Journal of the China Railway Society，2010，32（1）：1-7.

［14］ 周文梁，史峰，陈彦，等.客运专线网络列车开行方案与运行图综合优化方法［J］.铁道学报，2011，33（2）：1-7.

ZHOU Wenliang，SHI Feng，CHEN Yan，et al. Method of integrated optimization of train operation plan and diagram for network of dedicated passenger lines［J］.Journal of the China Railway Society，2011，33（2）：1-7.

［15］ 周明，孙权栋.遗传算法原理及应用［M］.北京：国防工业出版社，1999：143-155.

高速铁路列车运行图结构优化研究

张小炳1，2， 倪少权1，2， 潘金山1，2

Optimization of Train Diagram Structure for High-Speed Railway

ZHANG Xiaobing1，2， NI Shaoquan1，2， PAN Jinshan1，2
（1.School of Transportation and Logistics，Chengdu 610031，China；2.National Railway Train Diagram Research and Training Center，Southwest Jiaotong University，Chengdu 610031，China）

To improve the carrying capacity of high-speed railway，the structure of the train diagram was optimized by drawing compact train diagram and designing reasonable operation scheduling for trains.The optimization problem of the train diagram structure was transformed into a traveling salesman problem（TSP）.Taking the total cost of the all routes as a goal，a 0-1 integer programming model was proposed，and then solved using the genetic algorithm.Finally，the model was verified through a real case study using the data of Beijing-Shanghai high-speed railway in 2015，and the optimized train diagram was compared with the original scheme.Computation results show that the total operation time of 39 trains was reduced from the 628 min in the original scheme to the 495 min in the optimized schedule，a reduction by about 21.2%.Therefore，the optimal alternative can meet better the demand for intensive dispatching during the peak period or in sudden burst condition of passenger flow.

railway transportation；train diagram；genetic algorithm；high-speed railway；carrying capacity；TSP

张小炳，倪少权，潘金山.高速铁路列车运行图结构优化研究［J］.西南交通大学学报，2016，51（5）：938-943.

0258-2724（2016）05-0938-06

10.3969/j.issn.0258-2724.2016.05.017

U292.41

A

2015-10-07

国家自然科学基金资助项目（61273242，61403317）；四川省科技厅软科学计划资助项目（2015ZR0141）；中国铁路总公司科技研究计划资助项目（2013X010-A，2014X004-D）

张小炳（1984—），男，博士研究生，研究方向为运输组织理论与系统优化，E-mail：zxbisme3@163.com

倪少权（1967—），男，教授，博士，博士生导师，研究方向为运输组织理论与系统优化，E-mail：shaoquanni@163.com

（中文编辑：秦萍玲 英文编辑：兰俊思）