基于博弈论的公平安全两方计算协议

（山西师范大学数学与计算机科学学院，山西临汾041004）

（山西师范大学数学与计算机科学学院，山西临汾041004）

针对传统安全两方计算无法实现完全公平性的问题，结合博弈论方法，将参与者看作是理性的，提出了理性安全两方计算协议.首先，在扩展式博弈框架下，给出安全两方计算的博弈模型；其次，根据博弈模型描述，给出理性安全两方计算理想函数FRPCP以及理性安全两方计算协议πRPCP；最后对协议的安全性、公平性及纳什均衡进行了分析.分析结果表明，在混合模型下，协议πRPCP能安全地实现理想函数FRPCP，并且在BDH困难假设下，协议πRPCP中各理性参与者的最佳策略是选择合作，当博弈达到纳什均衡时，参与者双方能公平地获得计算结果.

安全两方计算；扩展博弈；纳什均衡；公平性

安全两方计算是指两个相互独立的参与者，在不泄露自己输入的情况下通过一个密码协议计算给定的函数，最终每个参与者都可以得到函数的计算结果.安全两方计算是分布式密码学的关键技术，也是安全多方计算的基础，此概念由姚期智教授为了解决百万富翁问题而提出［1］，即两个百万富翁想知道他们谁更富有，但又不希望对方知道自己财富的多少，并针对该问题设计了第一个安全两方计算协议，后来Goldreich、Micali和Wigderson将安全两方计算的理论系统化，推广为多方参与的安全多方计算［2］问题，尤其是他们提出的理想/现实范式对后来的密码学研究具有重要的指导意义，正是这些开创性的研究工作吸引了许多专家学者积极投身于安全多方计算研究，并取得了一系列研究成果［3-10］.

理想/现实模拟范式是衡量安全多方计算协议安全性的标准.假设在理想世界中存在一个可信第三方，参与者将各自的输入发送给可信第三方，由可信第三方完成计算任务并将最终结果发送给各参与者，理想情况下的参与者是通过安全信道来传递自己的私有输入，并由安全第三方代替参与者完成计算过程，因此可以保证安全性.但是在现实情况下，找到可信第三方是非常困难的，参与者只能通过运行协议来完成计算.如果一个攻击者在攻击真实协议执行时所得到的信息并不能比其在理想模型下攻击所得到的信息多，就称此协议是安全的.显然，如果一个安全多方计算协议是安全的，那么攻击者就不可能得到任何有用信息.

目前已有的两方计算研究主要关注协议的安全性，忽略其公平性，而公平性在无可信第三方的情况下显得更为重要，公平性就是指参与双方要么都获得计算结果，要么都不能获得计算结果.Cleve曾指出两方计算中的完全公平性只有在诚实参与者占大多数的情况下才能实现［11］，该结论使安全多方计算公平性的研究一度陷入了困境.Goldreich等［4］提出了一个在任意模型下多方通用的、可以计算任意函数的安全多方计算协议，但该方法只有存在特殊单向函数的情况下才能实现，非常不实用.Gordon等［12］对某些特殊函数的安全多方计算协议的公平性进行了研究并得出结论，认为即使不存在诚实参与者占大多数的情形也可以实现完全公平性，为公平性的研究扩宽了领域.

安全多方计算可以看作是研究相互不信任的多个参与者之间的交互问题的，这个特点与博弈论的局中人非常相似，2004年由Halpern和Teague［13］首次提出了理性安全多方计算的概念，认为参与者都是理性的，所采取的策略和行动都是为了最大化自身利益.事实上，在现实生活中参与者之间的交互都会受到某些利益的驱动，他们通常会为了提高自己的收益而作出理性的选择，因此相比传统密码学中把参与者进行诚实和恶意的划分，将参与者看作是理性的假设更加接近现实生活，该研究引起了国内外研究者的关注.在文献［13］的协议中采用了重复剔除弱劣策略下的纳什均衡，但对于参与者大于两个的情况不适用，协议执行过程中要求分发者一直在线，并且不能防止成员合谋；Kol和Naor［14］发现重复剔除方法并不能排除所有不好的策略，提出了严格纳什均衡及计算性C-resilient均衡，但该方案不能防止参与者在安全多方计算阶段欺骗；Abraham等［15］为理性参与者定义了一个抗合谋均衡且给出了一个可以抵抗最多k人合谋的协议；Lysyanskaya等［16］定义了该模型下的纳什均衡，利用理想/现实范式分析了具有理性和恶意参与者的混合模型下的安全多方计算问题，满足恶意敌手控制［n/2］-2局中人时，协议仍然能达到纳什均衡；Asharov等［17］讨论了理性条件下的多方安全计算的一些基本性质，认为公平性在特定函数和收益设置下不可能达到；Groce等［18］在此基础上进行了深入研究，认为只要参与者有严格动机计算理想环境中的函数，就可以实现理性公平计算；张恩和蔡永泉［19］针对传统两方安全计算协议中存在的不公平性，构建了两方计算协议的博弈模型，最终能公平地得到计算结果；王伊蕾等［20］讨论了理性两方安全计算的序贯结构，构造了更加复杂但是更实际的理性计算协议，利用序贯均衡的概念保证协议的公平性.

从所引文献可见，理性安全两方计算协议的公平性是当前密码学研究的一个热点.但已有的理性安全多方计算协议存在以下问题：（1）只讨论了协议的安全性和隐私性，不能保证完全公平性；（2）在协议中使用了信封和投票箱等较强的物理通道，这种假设在现实中不适用；（3）由于理性参与者的自利行为，导致协议中出现参与者不合作的行为，类似于博弈论中囚徒困境现象，无法实现协议的公平性.本文从扩展博弈的角度出发研究两方计算的公平性问题，首先给出安全两方计算的博弈模型，为每个参与者设计不同策略，当理性参与者偏离所设计策略时，其获得收益不会比其遵守策略时大，当博弈达到均衡状态时，参与者要么都能获得正确的计算结果，要么都不能获得，因此模型满足两方计算的公平性定义；其次利用双线性对技术设计了理性两方计算协议，通过对参与者收益函数的设置，使得遵守协议是参与者的最优策略；最后利用理想/现实范式对协议的安全性进行了证明.

1 基础知识

1.1 双线性对

定义1（双线性对） 设（G1，+）和（G2，·）为两个阶数均为素数p的循环群，其中前者为加法群，后者为乘法群.令P为G1的生成元，如果满足下面的性质，称变换e∶G1×G1→G2为双线性对.

（1）双线性：对任意P1、P2和Q∈G1有

e（P1+P2，Q）=e（P1，Q）e（P2，Q）及e（Q2，P1+P）=e（Q，P1）e（Q，P2）成立；

（2）非退化性：存在P∈G1即e（P，P）≠1，也就是说e（P，P）是G2的生成元；

（3）可计算性：对任意P1，P2∈G1，存在有效的算法计算e（P1，P2）.

定义2（可忽略函数） 函数μ（·）＜1/p（k）是可忽略函数，如果对任意正多项式p（·）和足够大的正数k都有μ（k）＜1/p（k）成立.

定义3（双线性Diffie-Hellman问题） BDH问题描述如下：在（G1，G2，e）中，给定（P，aP，bP， cP），对任意的a，b，c∈，计算e（P，P）abc∈G2.

根据定义3中可忽略函数的定义，BDH假设可描述为：在求解BDH问题上，没有概率多项式时间算法有不可忽略的优势.

定义4 两个总体 Xdef=｛Xn｝n∈N和 Ydef=｛Yn｝n∈N，如果对于每一个概率多项式时间算法D、每一个正多项式p（·）及所有充分大的n，都有

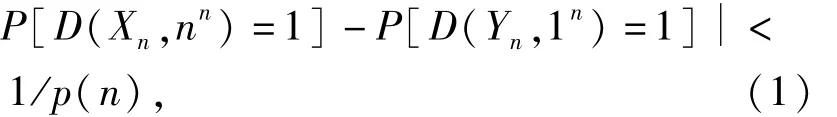
则称这两个总体是在多项式时间内不可区分的.

定义5（安全两方计算） 两个参与者P1和P2分别拥有秘密输入xi（i=1，2），共同执行协议Π来计算函数f（x1，x2）=（y1，y2）（y1可以和y2相等），计算结束后，P1得到y1，P2得到y2.在这个过程中，每个成员仅仅知道自己的输入数据和最后的结果.

定义6（安全两方计算安全性） 设f为一个实现安全计算的理想函数，Π为现实模型的协议. Π能够模拟理想函数f，当且仅当对于任意现实模型中的攻击者A，存在一个理想模型下的攻击者S，使得在任意的环境下，与真实环境下的攻击者A和协议Π交互还是与理想环境下的攻击者S和理想函数f交互是不可区分的，也就是说使得概率总体RΠ，A（¯x，y）与If，S（x，y）是计算不可分辨的，则称协议Π安全实现了理想函数f.

定义7（安全两方计算公平性） 如果安全两方计算协议中的参与者要么得到了计算结果，要么都没有得到计算结果，则称该协议满足公平性.

1.2 博弈论相关概念

博弈论主要研究利益存在冲突的决策主体在相互对抗中，对抗双方（或多方）相互依存的一系列策略和行动的过程集合.在分析其他参与方可能出现的行为策略基础上，理性参与者会选择对自己最有利的策略，均衡就是在参与方选择各自最优策略时所达到的一种稳定状态，这时任何参与方都不会单独改变策略，因为改变策略意味着自身利益的损失，因此没有人会愿意打破这一状态.

设P=｛P1，P2，…，Pn｝表示由n个参与者组成的集合，用ai表示参与者Pi的策略，A=（a1，a2，…，an）表示所有参与者的策略组合，a-i表示除Pi以外其他人的策略.o表示博弈的结果，ui（o）表示关于结果o的效益函数，令Oout（o）=（s1，s2，…，sn），如果参与者Pi最终得到了输出结果，则令si= 1，否则令si=0，令Oi=si.假设理性两方计算中的参与者总是希望得到输出结果，并且希望得到输出结果的参与者越少越好，则效用假设的形式化描述如下：

（1）U1：如果Oi（o）=Oi（o′），那么ui（o）= ui（o′）；

（2）U2：如果Oi（o）=1，Oi（o′）=0，那么ui（o）＞ui（o′）；

（3）U3：如果Oi（o）=Oi（o′），对于所有j≠i，有Oj（o）≤Oj（o′），并存在某个j满足Oj（o）＜Oj（o′），那么ui（o）＞ui（o′）.

动态博弈中参与者行为不是同时进行，而是先后选择.扩展博弈能够描述参与者决策的动态结构，每一个参与者轮流采取行动，而且其行动依赖于他们之前博弈的历史，参与者需要随着协议的进行选择新的行为，而如何选择则是由策略决定.

定义8（扩展式博弈） 一个扩展式博弈Γ是一个五元组（P，Q，p，（Ii）i∈P，（≤i）i∈P），其中P代表参与者集合，Q是行动序列集合，且满足如下性质：

（1）空序列φ属于Q；

（2）如果ak∈Q，k=1，2，…，w和0＜v＜w，那么ak∈Q，k=1，2，…，v；

（3）如果无限行动序列ak∈Q，k=1，2，…，∞满足ak∈Q，k=1，2，…，v对任意正整数v，则ak∈Q，k=1，2，…，∞.

①p是参与者函数，它赋给每个非终端序列（Q＼Z的元素）一个P的元素；

②Ii是参与者i∈P的信息集，它表示参与者进行选择时所知道的信息；

③≤i是参与者的偏好关系：对每个i∈P有一个Z上的偏序关系.

扩展博弈的解释如下：每个Q中的行动序列代表博弈的可能历史.空序列φ代表博弈的开始节点，每个参与者轮流采取行动，而且其行动依赖于他们之前博弈的历史，每个参与者拥有一个节点，参与者从该节点出发所采取的行动会引出指向另外节点的一条边，终端集合Z代表博弈所有可能的结果（outcomes）.如果将一个扩展式博弈看成是一棵博弈树，树的边和节点分别对应博弈的行动和行动序列.

定义9（纳什均衡） 在博弈Γ=（Ai，ui），i= 1，2，…，n中，称行为策略a∈A达到纳什均衡.如果对于任意参与方Pi∈P有

两方扩展式博弈可记为（｛P1，P2｝，｛A1，A2｝，｛u1，u2｝），其纳什均衡表述为

ui（ai，a-i）≥ui，a-i），

纳什均衡是指参与者在选择各自最优行为时的状态，是一个稳定的状态，在其他参与者不改变策略的情况下没有人愿意偏离这个状态.相关博弈论的详细知识请参阅文献［21-22］.

2 理性两方计算博弈模型

理性安全两方计算是指参与者为理性的安全两方计算协议，与传统安全两方计算最大的区别在于参与者根据他们的效用来决定是否遵守协议.

两方计算博弈中的参与人就是安全两方计算的参与者，策略是协议中允许的行为，博弈的过程按照协议执行流程来进行，由于在每一轮协议执行之前，各参与者均不知道对方可能采取的策略，只有当收到对方发送的结果并进行验证后才能确定其行动，可见该博弈是不完全信息动态博弈，效用函数按照博弈结束时，每个参与人是否得到正确的计算结果来考虑.本节基于扩展式博弈建立两方公平计算博弈模型，称为安全两方计算博弈Γ.

2.1 参与人

用P=｛P1，P2｝表示安全两方计算博弈Γ的两个理性参与者，用T表示可信第三方.

2.2 信息集

最后终结于博弈的叶子节点.

2.3 策略集

参与者Pi在行动序列q后会依据其信息集和其效用函数选择下一步可行策略，其可行策略集合分为以下3类：

（1）按照协议的方式发送正确的信息，记为C；

（2）按照协议的方式发送错误的信息，记为D；

（3）不做选择或退出协议，记为Q.

在理性安全计算博弈中，每位参与者Pi可以在任何时候选择退出博弈，即选择策略Q；若没有选择策略Q，则参与者Pi可以在当前状态下给任何其他参与者发送信息，包括发送正确或者错误的信息，也即选择策略C或者D.

2.4 效用函数

对于理性参与者Pi（i=1，2），在以上效用假设下定义4种情况的效用值：

（1）ui（o）=a，只有Pi得到计算结果，另外的参与者没有得到；

（2）ui（o）=b，两个参与者都得到计算结果；

（3）ui（o）=c，两个参与者都没有得到计算结果；

（4）ui（o）=d，Pi没有得到计算结果，另外的参与者得到了.

如果参与者Pi在协议执行过程中选择退出策略Q，那么对于另外一个参与者来说，其最优选择也是选择策略Q，此时两个参与者的效用都为c；否则，如果其不选择Q，他的效用可能是d，而d＜c.

根据安全多方计算协议公平性的要求，在协议结束后，参与者要么都得到协议的正确计算结果，要么都得不到协议的正确计算结果.该公平性在该博弈模型下可表现为参与者双方均得到相同的收益.

3 公平的理性两方计算理想模型

本节阐述在理想情况下，公平的安全两方计算协议博弈模型，记该协议为FRPCP，称其为理想函数.具体分为以下5步：

给定需计算的二元函数f（x1，x2）∈，其中x1，x2∈；参与者集合 P=（P1，P2）.FRPCP处理如下：

（1）当 FRPCP从参与者 Pi∈P收到其输入（Pinput，Psid，w），如果存在 P′sid，使得 Psid=（P，），则

①将w赋值给xi，即xi=w；

③发送（Pinput，receipt，Psid）给Pi.

（2）当 FRPCP从参与者 Pi∈P收到（Pcompute， Psid，Pi），如果存在，使得Psid=（P，P′sid），则

当收到（P1，P2）的输入值，同时给每位参与者都发送回复消息（Pinput，receipt，Psid）后，FRPCP计算随机函数

f（x1，x2）=（f1（x1，x2），f2（x1，x2）），…，（f1，f2）.

（3）当FRPCP从参与者Pi∈P收到公平输出消息（Pfair.output，Psid，Pi），如果存在 P′sid，使得 Psid=（P，P′sid），则

①若当前存在被标识为“贿赂”的参与者，则给其发送中断符⊥，给其余参与者发送相应的fi；

②否则，给每位参与者Pi发送fi.

（4）当从敌手S收到（Pcorrupt.input，Psid，Pi），如果存在P′sid，使得Psid=（P，P′sid），则

①登记Pi是“被贿赂的”；

（5）当从敌手S收到（Pcorrupt.input，Psid，Pi），如果存在，使得Psid=（P，），则

①登记Pi是“被贿赂的”；

②转发fi给敌手S；

③如果当前敌手S提供另一个值w′，并且计算函数的输出阶段其输出值fi还没有写在Pi的输出带上，则置xi=w′.

在该理想函数中，参与者输入的保密性由其理想函数FRPCP的第（1）步保证；计算输出的正确性由第（2）步保证；根据上节在博弈模型下公平性的说明，即参与者有相同的收益，该性质由第（3）步保证；其安全性由第（4）和（5）步保证.

4 公平的理性两方计算协议

本节利用双线性对技术，设计理性公平计算协议，记该协议为πRPCP.

根据定义5中安全两方计算协议的定义，两个参与者分别拥有秘密输入xi（i=1，2），共同计算函数f（x1，x2）=（y1，y2）（y1可以和 y2相等）.设（G1，+）和（G2，·）分别为p阶加法循环群和乘法循环群，p为素数.令P、Q和R为G1的生成元，并且其间的离散对数问题无人知道.e∶G1×G1→G2为双线性对.该协议包括3个阶段：数据准备阶段、数据交互计算阶段和结果输出阶段.

4.1 数据准备阶段

令x1和x2作为P1和P2的私有输入（如果任意一方的输入是无效的，则该协议给双方发送中断符⊥）.

P1执行如下：

步骤1 根据几何分布随机从｛1，2，…，p｝选取t1（其中p是群G1的阶）；

说明 选取多项式次数服从几何分布是为了让参与者双方的多项式尽量分布在群阶数p的中间位置，避免出现多项式的次数过高和过低的情况；

步骤2 生成两个次数为t1-1的多项式f（x）和g（x）：

式中：x1=a0+b0；

步骤3 计算承诺对

C10=e（a0P+b0Q，R），C11=e（a1P+b1Q，R），…，C1t-1=e（at-1P+bt-1Q，R），并公布C1i，其中0≤i≤t1；

步骤4 计算ri=f（i）和si=g（i），令x10=（0，r0），x11=（s0，r1），x12=（s1，r2），…，x1i=（si，ri+1），…，x1n=（si-1，ri），x1n+1=（sn，0），并保密x1i，其中i=1，2，…，n＞t1.

P2执行如下：

步骤1 根据几何分布随机从｛1，2，…，p｝选取t2（其中p是群G1的阶）；

步骤2 生成两个次数为t2-1的多项式f（x）和g（x）：

式中：x2=a0+b0.

步骤3 计算承诺对

C20=e（a0P+b0Q，R），C21=e（a1P+b1Q，R），…，C2t-1=e（at-1P+bt-1Q，R），并公布C2i，其中0≤i≤t2；

步骤4 计算ri=f（i）和si=g（i），令x20=（0，r0），x21=（s0，r1），x22=（s1，r2），…，x2i=（si，ri+1），…，x2n+1=（sn，0），并保密 x2i，其中 i=1，2，…，n＞t2.

4.2 数据交互计算阶段

步骤1 参与者P1给参与者P2发送x10，P2给参与者P1发送x20.

步骤2 参与者P1给参与者P2发送x11，P2给参与者P1发送x21.同时，P1通过式（4）验证在上一轮收到数据的正确性，若式（4）成立，则继续；否则，则终止协议.

P2通过式（5）验证在上一轮收到数据的正确性，若式（5）成立，则继续；否则，则终止协议.

在第i轮，i∈｛1，2，…，n｝，参与者P1给参与者P2发送x1i，P2给参与者P1发送x2i.同时，P1通过式（6）验证在上一轮收到数据的正确性，若式（6）成立，则继续；否则，则终止协议.

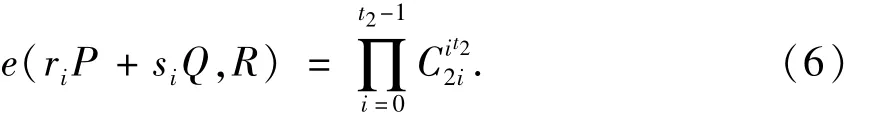
P2通过式（7）验证在上一轮收到数据的正确性，若式（7）成立，则继续；否则，则终止协议.

此阶段结果输出说明：协议总共n+1轮，在每一轮参与者按照以下规则决定自己的输出：

（1）在协议第i轮，如果P1在P2收到x1i之前终止协议，则P2将随机决定他的输出；如果P2在P1收到x2i之前终止协议，则P1也将随机决定他的输出，并根据输出结果是否正确获得一定收益值；

（2）如果P1遵守协议规则正常运行结束，且每一轮均通过验证，则P2将输出正确的x2i；如果P2遵守协议规则正常运行结束，且每一轮均通过验证，则P1将输出，并根据输出结果是否正确获得一定收益值x1i.

4.3 结果输出阶段

此阶段分如下两步：

步骤1 如果第一阶段（数据准备阶段）和第二阶段（数据交互计算阶段）均顺利完成，则参与者根据第二阶段收到的信息，利用拉格朗日插值多项式重构收到的信息，最后计算出f（x1，x2）的值；

步骤2 如果第一阶段（数据准备阶段）和第二阶段（数据交互计算阶段）均未完成，则参与者随机输出f（x1，x2）的值.

5 方案分析

本节对所构造的协议进行安全性、公平性及纳什均衡分析.

定理1 在BDH困难假设下，所构造的理性安全公平计算协议πRPCP是安全的和公平的，即协议πRPCP能安全实现其理想函数FRPCP.

证明 设A是现实中的敌手与实际协议πRPCP中的参与者交互，并运行理性安全公平协议πRPCP，同时构造理想博弈模型下的敌手S，使得任何区分器Z均不能以不可忽略的概率区分：在混合模型下（记为REAL）A与敌手和理性安全公平计算协议πRPCP交互，还是在理想博弈模型（记为IDEAL）下与理想敌手S与理想博弈模型FRPCP交互.

构造理想敌手S：敌手S运行A的一个仿真副本，来自区分器Z的任何输入都转给敌手A，同时A的任何输出都将拷贝给S作为其输出.

5.1 仿真可信第三方（TTP）

当一个可信的TTP被激活，S从FRPCP得到相关激活信息，并为敌手S仿真协议πRPCP.

5.2 仿真发送者

当未被攻陷的参与者通过输入激活消息被激活，仿真敌手通过FRPCP得到该消息，同时为A仿真协议πRPCP.

（1）当S从FRPCP得到参与者P′1激活消息，S发送该消息给A，然后转发A的回复给FRPCP.

（2）当S从FRPCP得到参与者P′2激活消息，S发送该消息给A，然后转发A的回复给FRPCP.

5.3 仿真接收者

当未被攻陷的参与者通过输入激活信息被激活，S从FRPCP得到该信息，同时为A仿真协议πRPCP.

5.4 仿真攻陷

当现实敌手A攻陷某一参与者，则S也攻陷该位参与者，同时将该参与者的内部状态提供给FRPCP.在此要求任何参与者均不存在任何形式的秘密内部状态.

IDEAL和REAl的不可区分性：基于所构造的理想敌手S，定义3类事件，同时证明下述3类事件中，无论哪一类事件发生，在BDHP假设下，其IDEAL和REAL均是不可区分的.

事件1 当某参与者Pi被攻陷，很容易观察到，在 REAL环境下，根据理想博弈模型、协议πRPCP的程序规则，可知S能完美仿真协议操作.因此，在此情况下，REAL和IDEAL是不可区分的.

事件2 当某参与者Pi被攻陷，在协议πRPCP执行过程中，Pi试图从公开信息中推断出对方的秘密输入信息，根据多项式的构造以及BDH假设可知，此时S能完美完成仿真协议操作.故此情况下，REAL和IDEAL是不可区分的.

事件3 当某参与者Pi被攻陷，在协议πRPCP执行过程中，试图以提前终止协议获得收益，根据理想模型FRPCP和协议πRPCP程序规则可知，在此情况下S能完美仿真协议操作.所以在此情况下REAL和IDEAL是不可区分的.

定理2 在BDH困难假设下，协议实例πRPCP执行中各理性参与者的最佳策略是C，即选择互相合作，此时各参与者的效用均为b.

证明 根据第3节（3）理想函数FRPCP的输出结果，即当FRPCP从参与者Pi∈P收到公平输出消息（Pfair.output，Psid，Pi），如果存在 P′sid，使得 Psid=（P，P′sid），则：

（1）若当前存在被标识为“贿赂”的参与者，则给其发送⊥，而给其余参与者发送相应的fi；

（2）否则，给每位参与者Pi发送fi.

又因为a＞b＞c＞d，每位参与者的最佳选择是选择策略C，否则他们将得到更差的收益.因此，在理想函数FRPCP中，其最优策略是C，当博弈达到纳什均衡时，各理性参与者得到的效用均为b.

另一方面，在协议的数据准备阶段和数据输出阶段，均是理性参与者独立完成计算任务，不存在破坏协议公平性的问题.在数据交互阶段，当协议执行到第i轮时，算法仅能验证上一轮i-1所收到数据的正确性.如果参与者在第i-1轮选择策略Q或者D，此时其收益最多为c，因协议双方必须多执行一轮，才能彼此验证对方收到信息的正确性.故在数据交互的整个过程中，参与者无论在哪一轮出现背叛，均不可能增加受益，因此协议双方的最佳策略是相互合作.

根据定理1的结果可知，协议πRPCP在BDH假设下能安全实现理性函数FRPCP，又因为在理想函数FRPCP下其理性参与者选择合作，其效用为b.因此，根据定理1中仿真证明过程可知，协议πRPCP满足公平性要求.根据定理证明过程中事件的证明，以及第4节协议πRPCP的博弈论模型可知，协议执行最终的纳什均衡为各参与者互相合作，在协议行动序列的每一步均将选择策略C，此时各方的收益均为，即所有参与者都能得到计算结果.

在协议性能方面，由于该理性公平计算协议是基于扩展式博弈建立的，因此可达到较强的纳什均衡，满足序贯均衡性质.在协议通信复杂度方面，其通信复杂度为n，是随机选取的大于门限t的数，故其通信轮数为常数，与文献［10］的通信轮数相当，但优于文献［13，19］的通信轮数O（k）（k为安全参数）.

6 结束语

安全两方计算协议中的公平性问题是密码学中的一个难题，本文结合博弈论方法对其进行了研究.首先基于扩展博弈提出了理性安全公平两方计算协议的博弈模型；其次根据博弈模型，对理性安全两方协议的安全性和公平性进行了分析，给出了其博弈模型下理想函数FRPCP，在此基础上基于双线性对技术，构造了公平的理性安全两方计算协议πRPCP；最后在混合模型下证明了理性安全两方计算协议πRPCP能安全实现其理想函数FRPCP，并且分析了当两方博弈达到纳什均衡状态时，参与者双方能公平地获得计算结果.

［1］ YAO A C.Protocols for secure computation［C］∥Proc. of the23rd IEEE Symposium on Foundationsof Computer Science（FOCS）.LosAlamitos：IEEE Computer Society Press，1982：160-164.

［2］ GOLDREICH O，MICALI S，WIGDERSON A.How to play any mental game［C］∥Proc.of the 19th Annual ACM Symposium on Theory of Computing（STOC）. New York：ACM Press，1987：218-229.

［3］ GOLDWASSER S.Multi-party computation：past and present［C］∥ Proc. of the 16th Annual ACM Symposium on Principles of Distributed Computing.New York：ACM Press，1997：21-24

［4］ GOLDREICH O.Foundations of cryptography：volume 2，basic applications［M］. Cambridge：Cambridge University Press，2004：79-92.

［5］ BLAKE IF，KOLESNIKOV V.Strongcondition oblivious transfer and computing on intervals［G］∥Proc.of Advances in Cryptology.Berlin：Springer，2004：515-529.

［6］ 李顺东，戴一奇，游启友.姚氏百万富翁问题的高效解决方案［J］.电子学报，2005，33（5）：769-773.

LI Shundong，DAI Yiqi，YOU Qiyou.An efficient solution to Yao' millionaires' problem［J］. Acta Electronica Sinica，2005，33（5）：769-773.

［7］ LIN H Y，TZENG W G.An efficient solution to the millionaires problem based on homomorphic encryption［C］∥In ASIA crypto logy 2005.Berlin：Springer，2005：456-466.

［8］ LINDELL Y，PINKAS B.A proof of Yao's protocol for secure two-party computation［J］. Journal of Cryptology，2009，22（5）：161-188.

［9］ 唐春明，石桂花，姚正安.排序问题的安全多方计算协议［J］.中国科学：信息科学，2011，41（7）：789-797.

TANG Chunming，SHI Guihua，YAO Zheng'an.Secure multi-party computation protocol for sequencing problem［J］. Scientia Sinica Informationis，2011，41（7）：789-797.

［10］ 田有亮，彭长根，马建峰，等.通用可组合公平安全多方计算协议［J］.通信学报，2014，35（2）：54-62.

TIAN Youliang，PENG Changgen，MA Jianfeng，et al. Universally composable secure multiparty computation protocol with fairness［J］.Journal on Communications，2014，35（2）：54-62.

［11］ CLEVE R.Limits on the security of coin flips when half the processors are faulty［C］∥ In 18th Annual ACM Symposium on Theory of Computing.Berkeley：［s.n.］，1986：364-369.

［12］ GORDON D，HAZAY C，KATZ J，et al.Complete fairness in secure two-party computation［C］∥Proc of the 40th Annual ACM Symposium on Theory of Computing（STOC）.New York：ACM Press，2008：413-422.

［13］ HALPERN J，TEAGUE V.Rational secret sharing and multiparty computation［C］∥Proc of the 36th Annual ACM Symposium on Theory of Computing（STOC）. New York：ACM Press，2004：623-632.

［14］ KOL G， NAOR M. Games for exchanging information［C］∥Proc.of the 40th Annual ACM Symposium on Theory of Computing（STOC）.New York：ACM，2008：423-432.

［15］ ABRAHAM I，DOLEVD，GONENR，etal. Distributed computing meets game theory：Robust mechanisms for rational secret sharing and multiparty computation［C］∥Proc.of the 25th ACM symposium on Principles of distributed computing（PODC'06）. New York：ACM，2006：53-62.

［16］ LYSYANSKAYA A， TRIANDOPOULOS N. Rationality and adversarialbehaviorin multiparty computation［G］∥Proc.the 26th Annual Cryptology. Berlin：Springer，2006：180-197.

［17］ ASHAROV G，CANETTI R，HAZAY C.Towards a game theoretic view of secure computation［G］∥Proc. of the 30th Annual International Conference on the Theory and Applications of Cryptographic Techniques. Berlin：Springer，2011：426-445.

［18］ GROCE A，KATZ J.Fair computation with rational player［G］∥Proc.of the 30th Annual International Conference on the Theory and Applications of Cryptographic Techniques.Berlin：Springer，2012：81-98.

［19］ 张恩，蔡永泉.理性的安全两方计算协议［J］.计算机研究与发展，2013，50（7）：1409-1417.

ZHANG En，CAI Yongquan.Rational secure two-party computation protocol［J］. Journal of Computer Research and Development，2013，50（7）：1409-1417.

［20］ 王伊蕾，郑志华，王皓，等.满足可计算序贯均衡的理性公平计算［J］.计算机研究与发展，2014，51（7）：1527-1537.

WANG Yilei，ZHENG Zhihua，WANG Hao，et al. Rational fair computation with computational sequential equilibrium［J］.Journal of Computer Research and Development，2014，51（7）：1527-1537.

［21］ OSBORNE M，RUBINSTEIN A.A course in game theory［M］.Cambridge：MIT Press，2004：10-15.

［22］ KATZ J.Bridging game theory and cryptography：recent results and future directions［G］∥Proc.of the 5th Theory of Cryptography Conf（TCC 2008）.Berlin：Springer，2008：251-25.

基于博弈论的公平安全两方计算协议

王 洁

Fair Secure Two-Party Computation Protocol Based on Game Theory

WANG Jie
（College of Mathematics and Computer Science，Shanxi Normal University，Linfen 041004，China）

Since complete fairness cannot be achieved in traditional two-party computation，a rational two-party computation protocol，based on game theory，was proposed，which regards player as rational.At first，the game model of secure two-party computation was put forward in the extensive game framework.Secondly，according to the description of game model，the ideal function FRPCPof rational secure two-party computation and rational two-party computation protocol πRPCPwere presented. Finally，the security，fairness and Nash Equilibrium of protocol was analyzed.The analysis results show that the protocol πRPCPcan realize ideal function FRPCPsafely in the hybrid model；meanwhile，under the Bilinear Diffie-Hellman（BDH）assumption，the best strategy of the rational players is to choose cooperation；and when the game achieves Nash Equilibrium，all players can obtain the right results fairly.

secure two-party computation；extensive game；Nash Equilibrium；fairness

0258-2724（2016）05-0902-08

10.3969/j.issn.0258-2724.2016.05.012

TP309

A

2015-08-21

王洁（1977—），女，副教授，研究方向为信息安全，E-mail：lktwj0801@163.com

王洁.基于博弈论的公平安全两方计算协议［J］.2016，51（5）：902-909.

（中文编辑：唐 晴 英文编辑：周 尧）