桥梁非线性自激气动力参数解析识别

（1.西南交通大学风工程试验研究中心，四川成都610031；2.风工程四川省重点实验室，四川成都610031）

（1.西南交通大学风工程试验研究中心，四川成都610031；2.风工程四川省重点实验室，四川成都610031）

随着自激气动力的非线性部分在桥梁风致振动中地位的显现，非线性自激气动力参数的合理确定显得至关重要.结合非线性自激气动力的解析表达式，基于分状态强迫振动风洞试验，提出了一种特征系统实现算法和非线性最小二乘法相结合的非线性自激气动力参数的解析识别方法.理想平板数值仿真结果表明：在无噪声情况下，识别结果与理论值完全一致；在20%白噪声情况下，识别最大误差仅3.7%，表现出较强的抗噪声能力.非线性气动力仿真结果表明：解析法能够精确确定非线性自激气动力谐波阶数，在20%白噪声情况下，各谐波幅值及相位的识别最大误差仅3.2%.将解析法运用于实际风洞试验，进一步论证了该方法的可行性和有效性.

强迫振动；非线性自激气动力；参数识别

1971年，Scanlan等［1］引入航空领域颤振导数的概念，将桥梁主梁断面自激气动力表达为运动参数的线性函数.事实上，桥梁断面的自激气动力存在明显的非线性效应.Halfman［2］利用强迫振动法识别机翼颤振导数时，发现自激气动力频谱存在高阶谐波成分.Falco等［3］在利用强迫振动装置对墨西拿海峡大桥进行颤振导数识别时观察到自激气动力高阶谐波分量.陈政清等［4］在利用强迫振动装置进行颤振导数识别时，发现在钝体断面的自激气动力中，高阶谐波分量所占比例接近20%.廖海黎等［5］通过对流线型箱梁节段模型的风洞试验研究，发现在大振幅、大攻角条件下，非线性高阶谐波分量十分明显.Diana等［6-7］采用强迫振动装置对墨西拿大桥主梁断面的气动力进行研究，观测到桥面断面显著的高阶谐波分量，及自激气动力存在的明显迟滞现象.

非线性自激气动力的存在将直接影响桥梁的气动稳定性，因此需要对其进行数学描述，而关于非线性自激气动力的数学模型，已有不少研究成果，如：徐旭等［8］基于Maclaurin级数展开的非线性自激气动力表达式；Diana等［9］提出了以瞬态攻角和瞬态角速度为变量表示的非线性气动力表达式；Wu等［10］提出了基于Volterra泛函级数的非线性气动力模型；王骑等［11］基于Taylor级数，将Scanlan模型进一步拓展，建立了不同谐波分量叠加的非线性自激气动力数学模型.由于文献［11］的数学模型物理意义明确，能够清晰地表达各阶谐波分量，因此，本文非线性自激气动力模型采用Taylor展开的非线性自激气动力表示式.基于强迫振动装置，提出一种特征系统实现算法和非线性最小二乘法相结合的非线性自激气动力参数的解析识别方法.该方法可以准确地确定自激气动力的非线性阶数，并能精确识别出各阶自激气动力所对应的气动参数，具有抗噪声能力强、识别精度高、计算速度快等优点.该方法可用于分状态强迫振动识别非线性自激气动力气动参数，试验结果表明了该方法的有效性.

1 非线性自激气动力模型

根据文献［11］，将非线性自激气动力表示为速压与非定常气动力系数乘积的形式：

式中：

ρ为空气密度；

U为来流速度；

B为桥梁断面宽度；

CL、CM为非定常气动力系数；

（.h，h，.α，α）为断面的运动状态.

假设断面发生振动频率ω的单自由度简谐振动h=h0eiωt和α=α0eiωt，将非定常气动力系数在平衡位置展开为n阶Taylor级数，以CL为例.

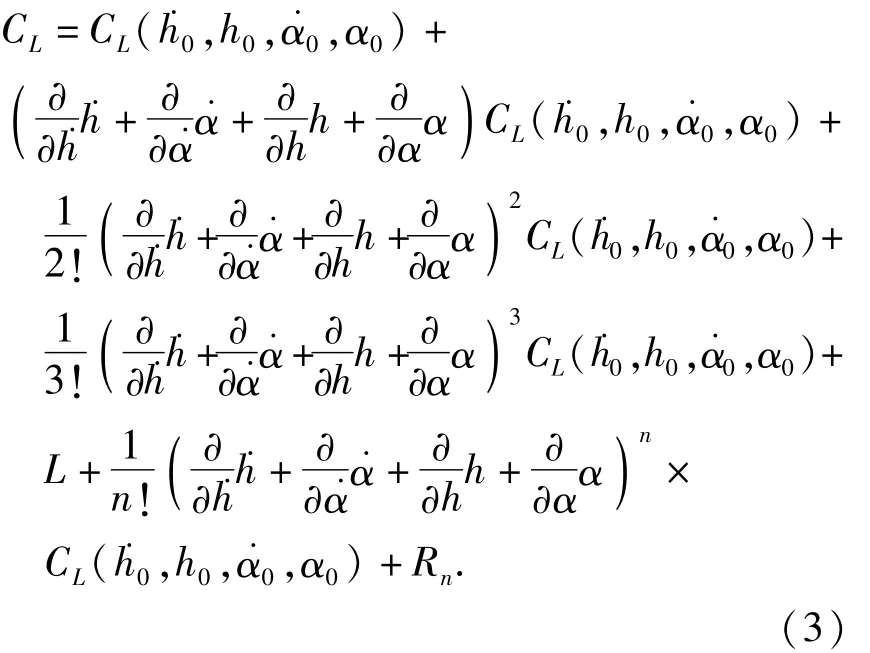
若断面仅发生单自由度竖向运动h=h0eiωt，省略定常项，自激升力系数为

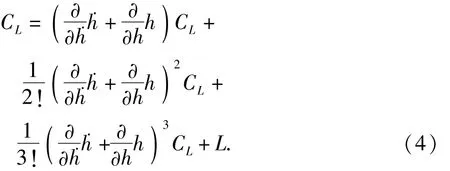
其中一次项与Scanlan线性自激气动力对应

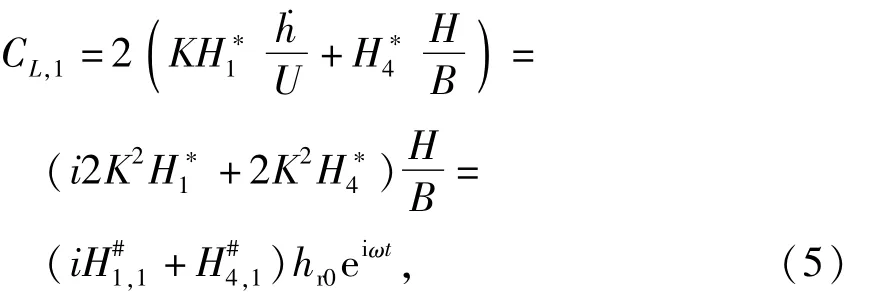
式中：

hr0=h0/B；

K=ωB/U；

由式（5）可看出，与非定常气动力系数一次项相关的气动参数包含了Scanlan自激气动力模型中的颤振导数.

非定常气动力系数二次项为

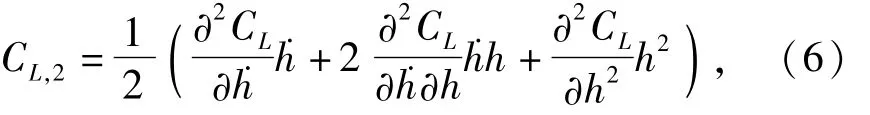
将与二次项有关的运动项代入

依此可得其它项的表达式，进而可得非定常气动力系数的标准表达式：

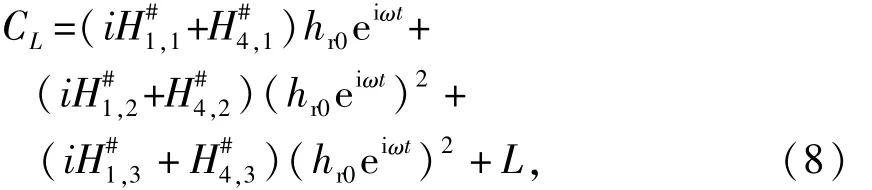
借助欧拉公式，将非线性自激气动力表达式由复数形式转化为实数形式，并根据实际测试和分析的需要取实部或虚部的运动形式.本文研究取虚部，即运动为正弦函数.由此，单自由度竖向运动引起的自激升力非定常气动力系数为同理可得其它3项非定常气动力系数.

由式（9）可知，若桥梁断面在强迫振动装置驱动下只发生稳态单自由度简谐运动，且存在非线性自激气动力分量的话，那么自激气动力将包含整数倍的谐波分量.若能识别出非线性自激气动力信号中各谐波分量所对应的幅值和初始相位参数，就可以从上述表达式中获得各阶自激气动力对应的气动参数.

2 参数识别方法

2.1 谐波阶次的确定

强迫振动产生的自激气动力信号为周期谐波信号，在确定信号谐波次数方面，经典的方法为功率谱估计（PSD），此外还有小波变化法、旋转矢量不变技术、奇异值分解（SVD）等.其中SVD具有抗噪能力高、计算精度高且速度快等优点［12-13］，SVD方法基本思路如下.

对采集数据信号Y构造的Hankel矩阵：

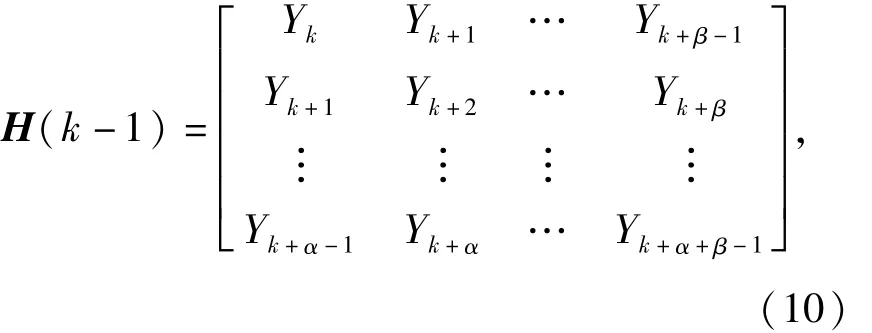
奇异值（SVD）分解：

式中：

U、V为奇异向量矩阵；

S为奇异值矩阵.

奇异值分解后可通过奇异值来确定谐波的阶次.如果奇异值按大小顺序排列有明显的突变，则突变处即是系统的阶次.但是在数据采集过程中会有随机噪声的存在，奇异值没有明显的突变分界线，因此可能无法从奇异值大小出发直观对系统进行定阶.

由于奇异值存在明显的特征：真实模态的值较大，虚假模态的值很小，随着阶次的增大，奇异值越来越小.基于这种现象，可以采用奇异值差值法来进行定阶［14］，简单的说就是将奇异值按大小顺序排列，并将相邻两值相减，通过差值趋于0这一条件来确定谐波阶次.

2.2 自激气动力的拟合

定义强迫振动测得自激气动力的模型为

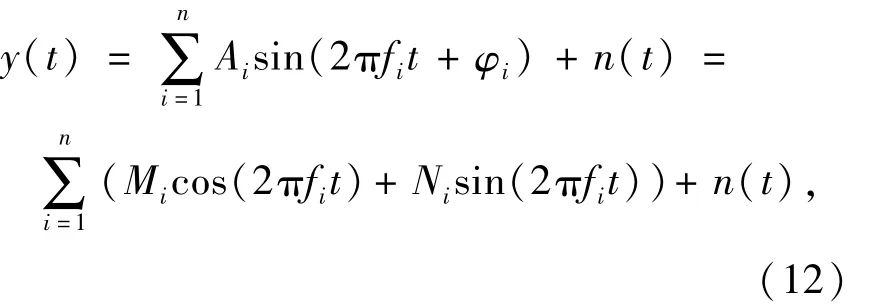
式中：

Ai、fi、φi分别为各谐波信号的幅值、频率和相位；

n（t）为噪声.

对强迫振动装置获得的自激气动力信号而言，高阶谐波频率是基频谐波的整数倍，只要获得了基频谐波频率，即可知高阶谐波频率.

在理想状态下，自激气动力的基频谐波频率应与装置的驱动频率完全一致，此时不需要对信号的频率进行识别，可直接采用驱动频率.但是，试验误差的存在会使自激气动力基频谐波频率与驱动频率存在微小差异.这时就需要对自激气动力的谐波频率进行精确识别，才能对其准确拟合，获得准确的幅值和相位值.信号频率的识别方法可以采用特征系统实现算法进行.

在确定系统阶数n之后，保留前n个奇异值和相应的奇异向量矩阵，就可得到系统的状态矩阵

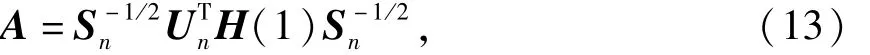
对系统状态矩阵A进行特征值分解：

由此可以得到A的特征值矩阵：

系统的频率为

在确定信号频率之后，各谐波的幅值和相位可以通过非线性最小二乘法来进行识别.

由式（12）可知各谐波的幅值和相位可表示为

式中：Mi=sin φi；Ni=cos φi.

将自激气动力表达式写成矩阵形式：

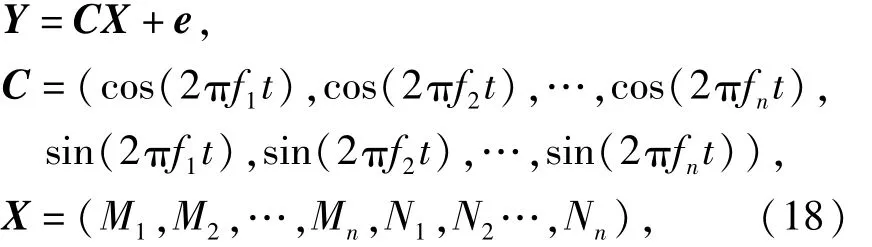
式中：e为识别误差向量.

2.3 气动力相位的确定

在进行分状态强迫振动试验识别气动参数时，不仅要采集自激气动力时程信号，还要同步采集位移时程信号.由式（9）可知，在利用解析方法识别自激气动力参数时，需要确定位移零相位所对应的自激气动力相位.具体方法如下：

（1）首先对采集的位移时程信号进行拟合，得到位移信号的初始相位φ.如单自由度扭转振动时位移拟合

（2）通过计算找到位移0相位所对应的时刻t0.如上面位移0相位对应的时刻

t0=（2π-φ）/2πf.

（3）自激气动力t0时刻的相位值即为所需要的相位值.在得到气动力相位值后就可以通过解析的方式识别气动参数.

3 数值仿真实验

3.1 理想平板颤振导数识别

模拟理想平板分状态强迫振动，通过解析方法识别平板的颤振导数来验证该方法的可行性.

分状态强迫振动频率设为2 Hz，强迫振动振幅3°，平板宽450 mm，试验风速10 m/s，采样频率为128 Hz.为计算方便，将纯扭转强迫振动位移初相位设定为0，理论位移谐波信号为

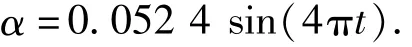
理论气动力动态系数谐波信号为

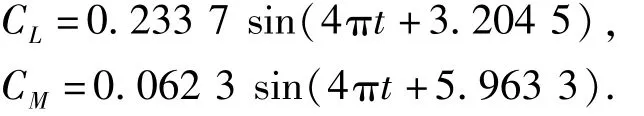
向位移信号和非定常气动力系数信号中各加入20%的白噪声，含噪声的非定常气动力系数时程信号如图1所示.对不含噪声和含噪声的信号进行气动参数识别，采用上述解析方法对颤振导数进行识别，表1为识别结果.由结果可知，在无噪声情况下，解析方法对颤振导数能精确地识别，在含20%噪声情况下，该方法的识别误差最大仅为3.706%，可见上述识别方法可以应用于小振幅下分状态强迫振动的颤振导数识别，并且具有较强的抗噪声能力和较高的识别精度.

3.2 非线性气动力参数识别

以自激升力动态系数为例，构造四阶正弦谐波信号，其中一阶基频f=2 Hz.各谐波参数分别设定为

谐波模型为

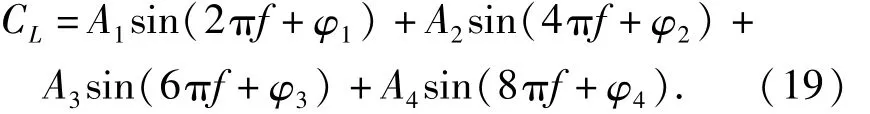
可以看出，高阶谐波振幅分别为一阶谐波振幅的20%、10%和5%.可见该信号为非线性较强的信号.向原始信号中加入20%的白噪声，然后运用解析法对各谐波的参数进行识别，表2为参数识别结果.

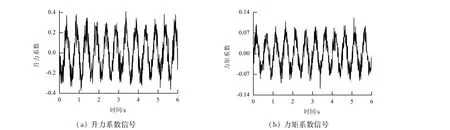
图1 含噪声非定常气动力系数信号Fig.1 Unsteady aerodynamics coefficient signal with noise

由识别结果可知，识别误差最大仅为3.224 7%，这说明解析法具有很好的抗噪声能力，能够较精确地对非线性自激气动力谐波信号的参数进行识别.

在进行参数识别时，还需利用该方法对同步采集的时程位移信号进行参数识别，找到相位为0所对应的时刻，然后利用自激力解析表达式识别出各阶谐波对应的气动参数.

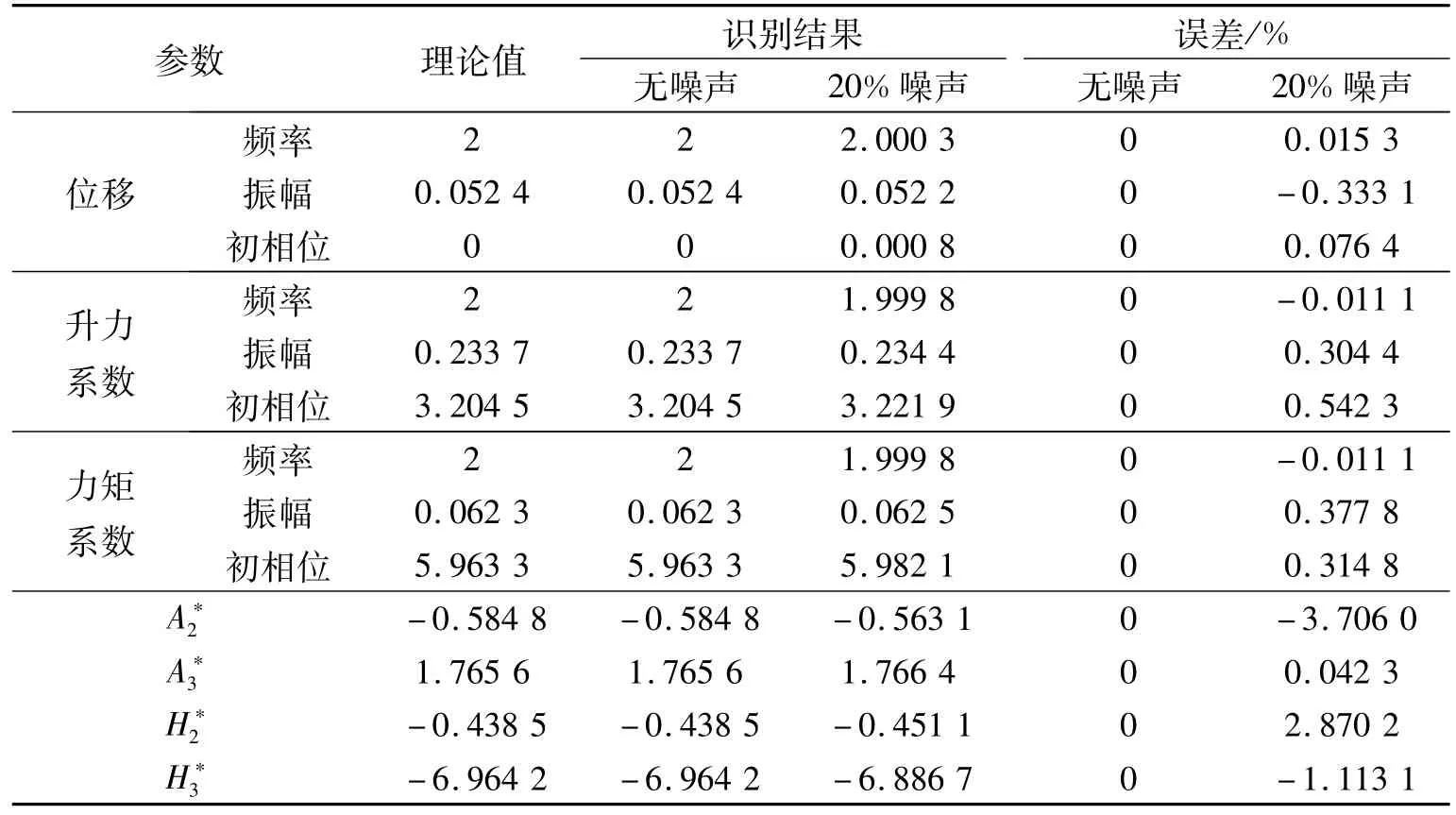
表1 理想平板颤振导数识别结果Tab.1 Identification results of flutter derivatives for ideal flat plate

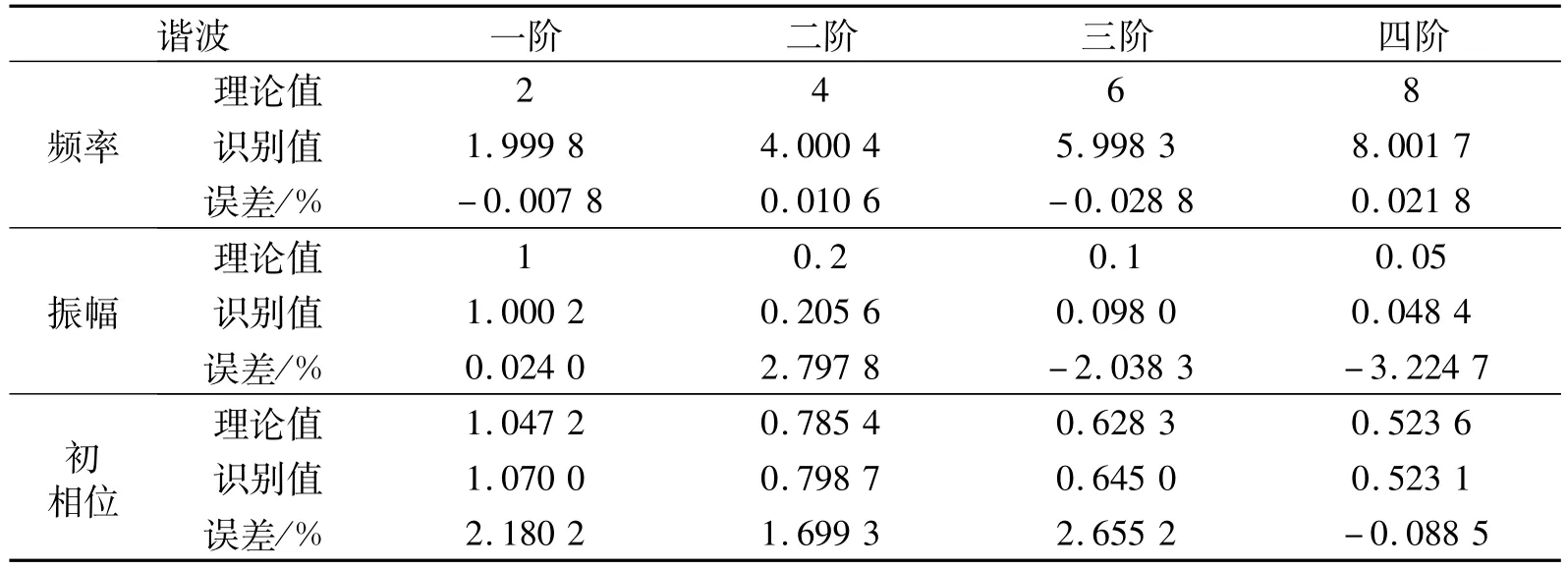
表2 非线性气动力参数识别结果Tab.2 Identification results of nonlinear aerodynamic parameter

4 风洞试验

利用强迫振动装置，基于1∶70的刚性节段测压模型和电子压力扫描阀，运用解析方法对断面的非线性自激气动力参数进行识别，以验证该方法的可行性.

桥梁节段模型强迫振动系统具有4套伺服电机驱动系统，可单独驱动节段模型作单自由度竖向或扭转运动，驱动时可实现常振幅、常频率的稳态振动.试验选取某一流线型箱梁断面进行，模型高0.050 m，宽0.554 m，长1.500 m，采用玻璃钢纤维和碳纤维制作.断面如图2所示.试验采样频率设置为128 Hz，采样时长为32 s，气动力在不同时刻对应的位移由强迫振动装置的测量系统采集.图2为模型断面图，图3为试验现场图片.

试验针对单自由度扭转振动进行.由文献［5］可知，在大攻角、大振幅条件下，桥梁断面自激力的非线性特性较明显.因此，试验选择在攻角α=5°，振幅A=10°下进行.表3为试验具体工况.

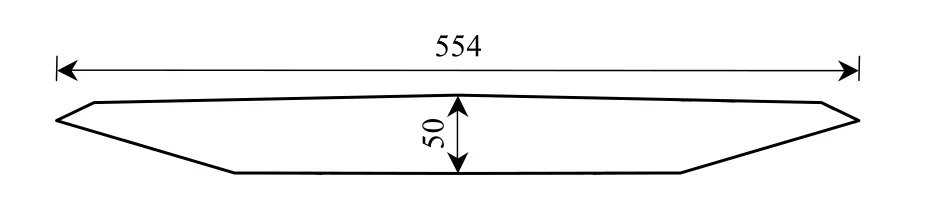
图2 流线型箱梁断面Fig.2 Streamlined box girder section

图3 强迫振动风洞试验Fig.3 Wind tunnel test for forced vibration

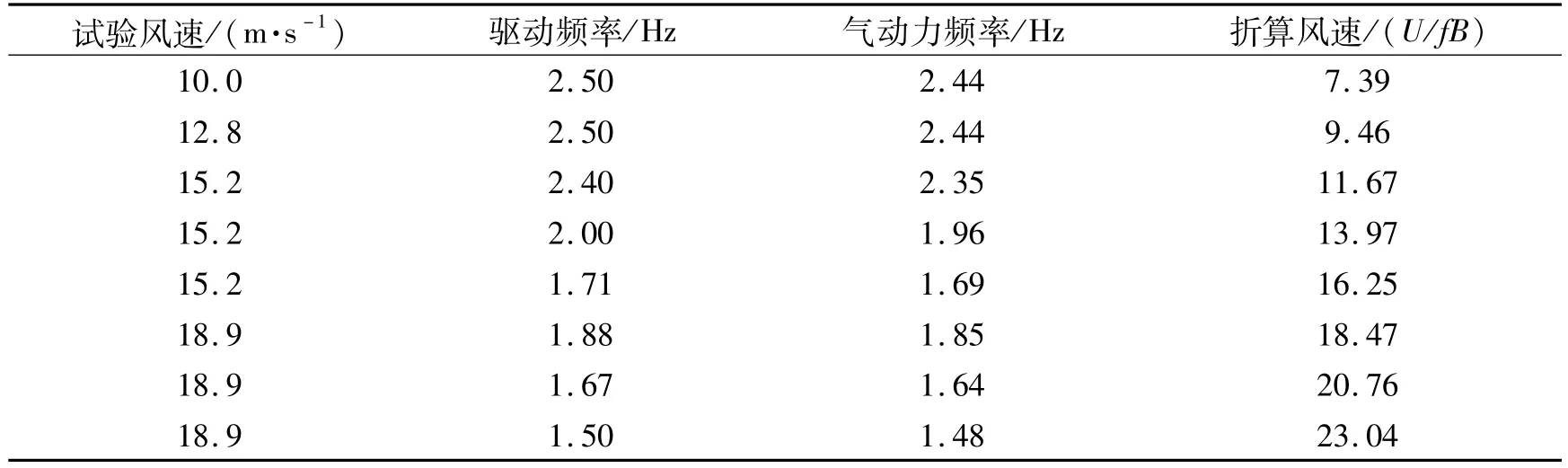
表3 试验参数Tab.3 Test parameters

采用上述解析方法对试验获得的非线性自激气动力信号进行拟合.拟合结果显示：非线性自激气动力谐波阶次均为3次；气动力的频率与驱动频率存在微小的差异（见表3）；自激气动力具有明显的非线性性质，其中，升力的基频谐波幅值比重在88%～91%之间，升力矩相应的值在64%～76%之间；自激气动力线性成分随折算风速增大而减弱.图4为折算风速23的非线性自激气动力谐波信号及拟合结果.基于同步采集获取的位移信号，识别出断面的非线性自激气动力参数（见图5）.

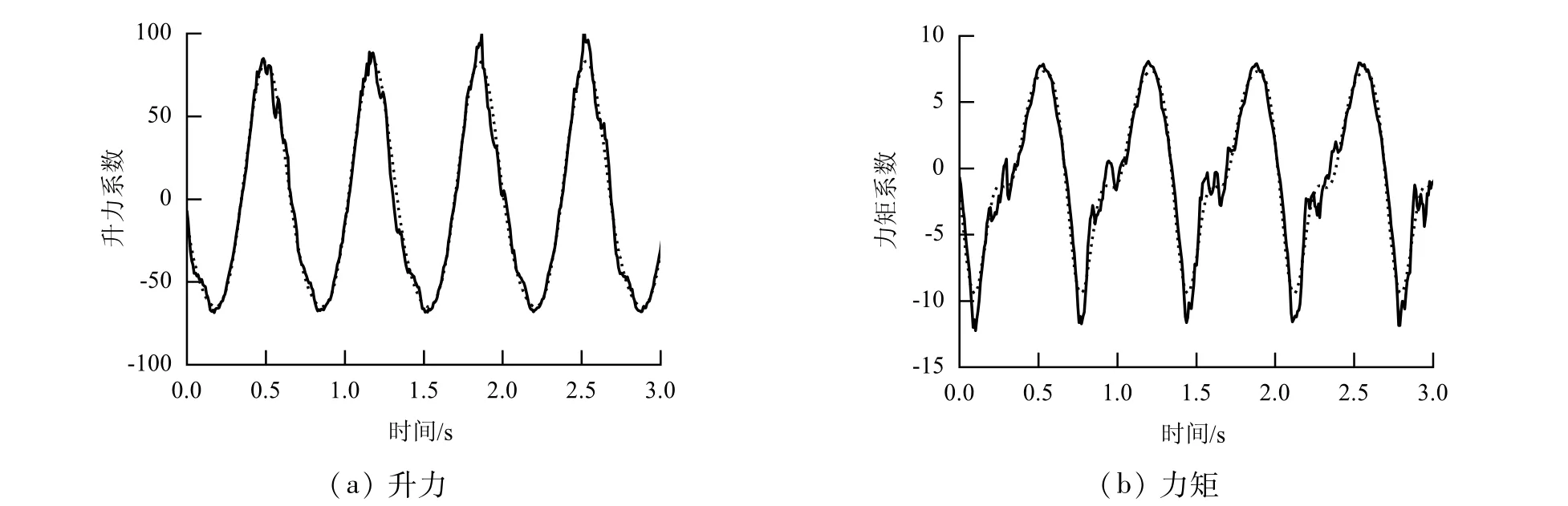
图4 自激气动力谐波信号及曲线拟合Fig.4 Harmonic signal of motion-induced aerodynamic forces and curve fitting

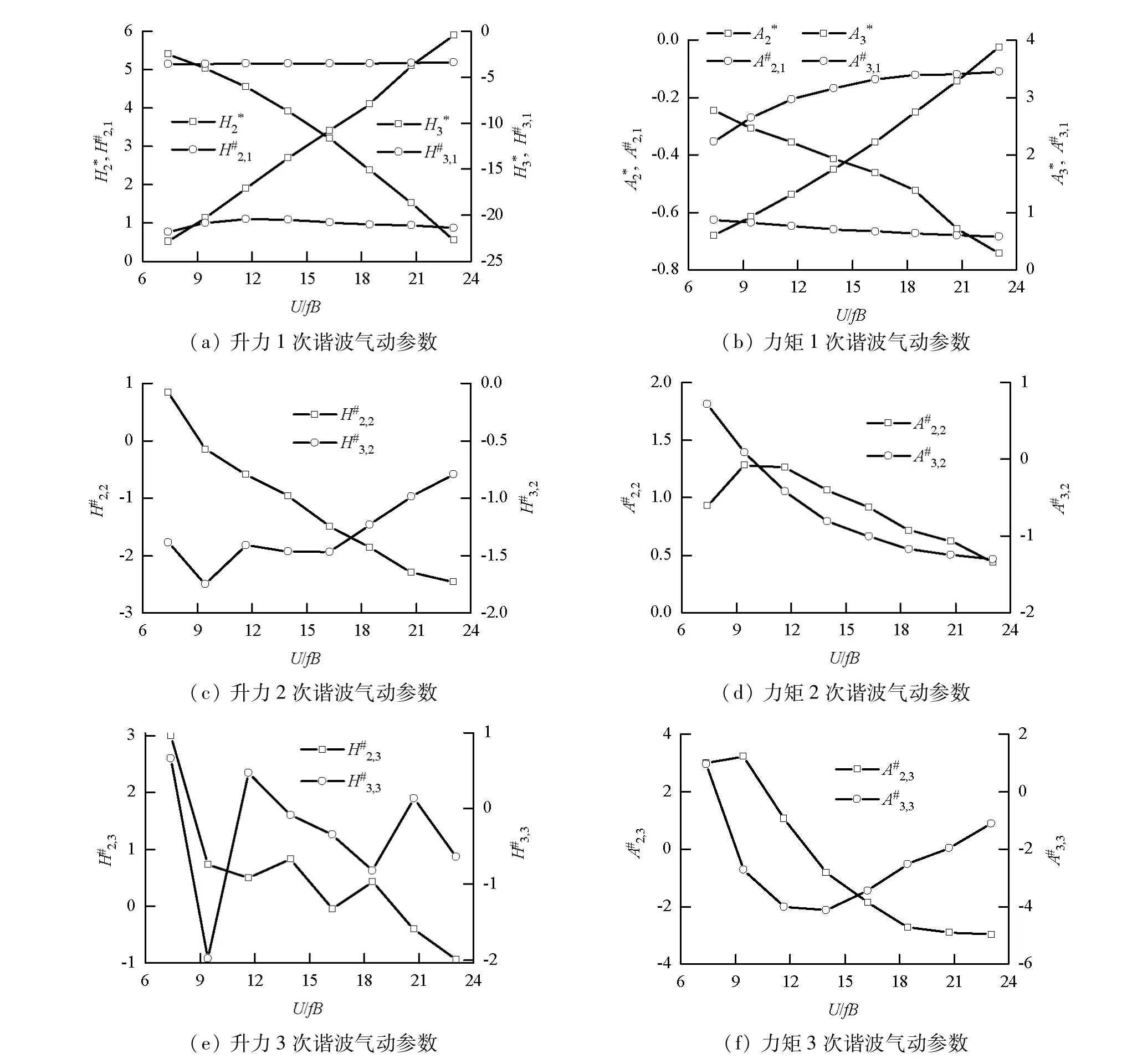
图5 非线性自激气动力参数Fig.5 Parameters of nonlinear motion-induced aerodynamic force

5 结 论

结合分状态强迫振动试验，提出一种解析方法用于桥梁非线性自激气动力参数识别.该方法具有较强的抗噪声能力，识别精度较高，能够对非线性高阶谐波项做出很好的辨识，可以应用于分状态强迫振动法识别非线性自激气动力参数，具有一定的实际意义.

数值仿真实验结果表明，该方法能够直接识别出含噪自激力信号的频率、振幅及相位参数，并可以准确地判定非线性自激气动力中高阶谐波的阶数，在此条件下，运用非线性自激力解析表达式可以识别相应的气动参数.风洞试验也进一步证明了该方法的可行性.

［1］ SCANLAN R H，TOMKO J.Airfoil and bridge deck flutter derivatives［J］. Journal of Engineering Mechanics，ASCE，1971，97（6）：1717-1737.

［2］ HALFMANR L.Experimental aerodynamic derivatives of a sinusoidally oscillationg airfoil in two-dimensional flow［R］.USA：NationalAdvisoryCommitteefor Aeronautics，1948.

［3］ FALCO M，GURAMI A，ZASSO A.Nonlinear effects in sectional model aeroelastic parameters identification［J］. Journal of Wind Engineering and Industrial Aerodynamics，1992，42（1/3）：1321-1332.

［4］ 陈政清，于向东.大跨桥梁颤振自激力的强迫振动法研究［J］.土木工程学报，2002，35（5）：34-41.

CHEN Zhengqing，YU Xiangdong.A new method for measuring flutter self-excited forces of long-span bridges［J］.China Civil Engineering Journal，2002，35（5）：34-41.

［5］ LIAO H L，WANG Q，Li M S，et al.Aerodynamic hysteresis effects of thin airfoil and streamline box girder under large amplitude oscillation［C］∥Proceedings of the 13th International Conference on Wind Engineering（ICWE 2011）.Amsterdam：Multi-science Publishing Co.Ltd.，2011：539-540.

［6］ DIANA G，BRUNI S，ROCCHI D.A numerical and experimental investigation on aerodynamic nonlinearities in bridge response to turbulent wind［C］∥Proceedings of the 4th European&African Conference on Wind Engineering（EACWE 2005）.Prague：the Academy of Science of the Czech Republic，2005：84-85.

［7］ DIANA G，RESTA F，ROCCHI D.A new approach to model the aeroelastic response of bridges in time domain by means of a rheological model［C］∥Proceedings of the 12th International Conference on Wind Engineering（ICWE 2007）. Cairns：TheAustralasian Wind Engineering Society，2007：207-214.

［8］ XU X，CaoZ Y.New expressionsofnonlinear aerodynamic forces in civilengineering［C］∥Proceedings of the 3rd International Conference on NonlinearMechanics （ICNM 1998）. Shanghai：Shanghai University Press，1998：396-401.

［9］ DIANA G，RESTA F，ROCCHI D.A new numerical approach to reproduce bridge aerodynamic nonlinearities in time domain［J］. JournalofWind Engineering and Industrial Aerodynamics， 2008， 96（10/11）：1871-1884.

［10］ WU T，KAREEM A.Modeling hysteretic nonlinear behavior of bridge aerodynamics via cellular automata nested neural network［J］. Journal of Wind Engineering and IndustrialAerodynamics，2011，99（4）：378-388.

［11］ 王骑，廖海黎，李明水，等.桥梁断面非线性自激气动力经验模型［J］.西南交通大学学报，2013，48（2）：271-277.

WANG Qi，LIAO Haili，LI mingshui，et al.Empirical mathematicalmodelfor nonlinear motion-Induced aerodynamic force of bridge girder［J］.Journal of Southwest Jiaotong University，2013，48（2）：271-277.

［12］ 喻胜，陈光矩.一种检测噪声中正弦信号的SVD方法［J］.电子学报，2000，28（6）：108-110.

YU Sheng，CHEN Guangju.Detecting the sinusoidal signal in noise by the SVD method［J］. ACTA Electronica Sinica，2000，28（6）：108-110.

［13］ 李天云，袁明哲，郑波等.谐波和间谐波三参数识别的SSI-LS方法［J］.电力系统保护与控制，2011，39（10）：42-46.

LI Tianyun，YUAN Mingzhe，ZHENG Bo，et al.A method of three parameters of harmonics and interharmonics high accuracy detection based on SSI-LS［J］.Power System Protection and Control，2011，39（10）：42-46.

［14］ 周帮友，胡绍全，杜强.特征系统实现算法中的模型定阶方法研究［J］.科学技术与工程，2009，9（10）：2715-2722.

ZHOU Bangyou，HU Shaoquan，DU Qiang.Study about calculating the order of model in eigensystem realization algorithm［J］. Science Technology and Engineering，2009，9（10）：2715-2722.

桥梁非线性自激气动力参数解析识别

熊 龙1，2， 廖海黎1，2，王 骑1，2， 马存明1，2

Analytic Identification of Bridge Nonlinear Motion-Induced Aerodynamic Parameter

XIONG Long1，2， LIAO Haili1，2，WANG Qi1，2， MA Cunming1，2
（1.Research Center for Wind Engineering，Southwest Jiaotong University，Chengdu 610031，China；2.Key Laboratory for Wind Engineering of Sichuan Province，Chengdu 610031，China）

As nonlinearity component of motion-induced force plays a key role in wind-induced vibration of bridge，it is very important to reasonably determine the nonlinear aerodynamic parameters. According to the detached-forced vibration wind tunnel tests，an analytic identification method for nonlinear aerodynamic parameters，which combines the eigensystem realization algorithm and nonlinear least square，was proposed with consideration of the analytical expression of nonlinear self-excited force.Numerical simulation results of ideal flat plate show that the identification results are in good agreement with the theoretical values in the noise-free case，and the maximum identification error is only 3.7%when there is additional 20%Gaussian noise.It means that the proposed analytic method has strong anti-noise ability.In addition，the numerical simulation results of nonlinear aerodynamic force show that the analytic method can accurately estimate the order of nonlinear motion-induced aerodynamic force，and with additional 20%Gaussian noise，the maximum identification error of the phase and amplitude of each harmonic is only 3.2%.Finally，wind tunnel tests were carried out to verify the feasibility and effectiveness of proposed method.

forced vibration；nonlinear motion-induced aerodynamic force；parameter identification

熊龙，廖海黎，王骑，等.桥梁非线性自激气动力参数解析识别［J］.西南交通大学学报，2016，51（5）：824-831.

0258-2724（2016）05-0824-08

10.3969/j.issn.0258-2724.2016.05.002

TU997；U448.27

A

2015-07-29

国家重点基础研究发展计划资助项目（2013CB036300）；国家自然科学基金资助项目（51308478，51378442）

熊龙（1983—），男，博士研究生，研究方向为大跨度桥梁抗风，E-mail：xionglong210@126.com

（中文编辑：徐 萍 英文编辑：周 尧）