考虑拉索局部振动的铁路斜拉桥车桥耦合振动分析

雷虎军，李闻秋，李小珍

(1．福建工程学院 土木工程学院，福建 福州 350118；2．西南交通大学 土木工程学院，四川 成都 610031)



考虑拉索局部振动的铁路斜拉桥车桥耦合振动分析

雷虎军1，李闻秋2，李小珍2

(1．福建工程学院 土木工程学院，福建 福州 350118；2．西南交通大学 土木工程学院，四川 成都 610031)

为研究拉索局部振动对大跨度铁路斜拉桥及桥上列车动力响应的影响，基于索-桥动力相互作用理论，以(60.5+156+464+156+60.5)m五跨连续钢桁梁铁路斜拉桥为工程背景，分别建立考虑斜拉索局部振动的多桁架模型(MECS)和传统的单桁架模型(SECS)，采用动力分析程序BDAP V2.0，针对地铁B型车以不同车速通过该桥时的车-桥耦合振动响应进行了仿真计算。计算结果表明：考虑拉索局部振动后，出现大量纯索振型与索-梁耦合振型；桥上车辆受拉索局部振动的影响不大，但单桁架模型会高估斜拉桥塔顶的加速度响应。因此，在进行大跨斜拉桥动力响应分析时，拉索局部振动的影响不容忽视。

车桥耦合振动；斜拉桥；拉索局部振动；多桁架模型

拉索是斜拉桥的重要承力构件，具有柔度大、质量轻、阻尼小等特点。在大跨度斜拉桥中，长短不一的斜拉索自振频率覆盖范围大，在外部动荷载作用下，柔性拉索的振动可能与结构的整体振动耦合，引发索-梁共振，从而使结构的振动响应急剧增大[1-2]。随着我国斜拉桥技术的进步，作用在其上的车辆荷载越来越大，如果由于斜拉桥本身动力特性的原因使得斜拉桥在长期车辆荷载作用下发生大幅索-梁共振，将严重影响斜拉索的耐久性，并会威胁桥上列车的运行安全。

目前，关于拉索局部振动的研究已受到越来越多的关注，取得了一些研究成果[3-6]。Yang等[3]考虑斜拉索振动过程中的大位移及索力变化非线性特性，采用离散索单元建立斜拉桥模型，研究了主跨150 m斜拉桥拉索在移动荷载作用下的非线性振动；亢战等[4]建立了拉索在车辆荷载激励下的多自由度模型，通过数值方法研究了斜拉桥的共振问题；王涛等[5]研究了索-梁发生大幅度相关振动时的振动特性，得出斜拉桥的整体振动可能引起拉索的大幅振动；张鹤等[6]研究了桥梁结构在车辆荷载作用下的动力反应，同时，根据拉索端的振动时程研究了拉索的振动问题，讨论了拉索、桥梁、外部动力激励三者间的关系。然而，对于铁路斜拉桥，除了拉索与主梁可能出现的耦合振动外，还包括车辆与轨道、轨道与桥梁之间的耦合作用，系统及其复杂，因此，关于斜拉索局部振动对铁路斜拉桥车桥耦合振动影响的研究还较为少见。

本文在以往研究的基础上，采用自主研发的桥梁动力分析程序BDAP v2.0为计算工具，以某(60.5+156+464+156+60.5)m五跨连续钢桁梁斜拉桥为工程背景，分别建立了考虑斜拉索局部振动的多桁架模型(MECS)和传统的单桁架模型(SECS)，在分析其自振特性的基础上，通过数值积分得到了列车以不同车速通过该桥时两种模型主梁跨中、塔顶的振动响应以及列车的动力响应，探讨了拉索局部振动的影响，其研究结果可为大跨度斜拉桥动力分析模型的建立提供参考。

1　斜拉索-主梁相互作用模型

以往对斜拉桥进行动力分析时，大部分研究者将斜拉索模拟为单个桁架单元(single-element cable system，简称SECS)，并通过Ernst修正来考虑拉索的垂度效应[7-11]，在此模型中，拉索的振动质量被等效至两端，拉索的动力特性及振动对整个结构的影响被忽略，不能反映斜拉索的局部振动对桥梁以及桥上列车的影响。

为了在列车-桥梁耦合振动分析中考虑斜拉索局部振动的影响，本文在单桁架模型的基础上将每根斜拉索划分为多个链杆单元，即可得到能够反映斜拉索局部振动的多桁架模型(multiplier-element cable system，简称MECS)，如图1所示。

图1　多桁架模型示意图Fig.1 Schematic diagram of MECS model

2　列车-线路-桥梁动力分析模型

BDAP v2.0程序中的列车-线路-桥梁耦合振动分析模型是由车辆模型、轨道模型和桥梁模型按一定的轮轨关系和桥轨关系关联起来的耦合大系统，如图2所示。以下分别介绍该程序中的车辆、轨道和桥梁动力学模型以及轮轨、桥轨相互作用关系。

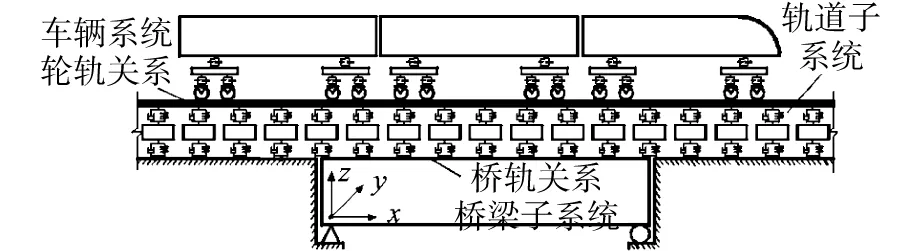
图2　列车-线路-桥梁耦合振动分析模型Fig.2 Dynamic model of vehicle-track-bridge coupled system

2.1车辆动力学模型

本研究中的车辆为二系悬挂四轴车辆，包含1个车体、2个转向架和4个轮对，共7个刚体，每个刚体考虑横移、侧滚、沉浮、点头和摇头5个自由度，刚体与刚体之间通过弹簧-阻尼原件连接，每辆车共35个自由度。采用D’Alembert原理，即可推导出车辆各子系统的动力平衡方程

(1)

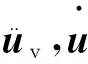
2.2轨道动力学模型

轨道动力学模型采用文献[12]介绍的板式无砟轨道结构。其中，钢轨被视为连续弹性离散点支撑上的无限长Euler梁，考虑横向、垂向和扭转自由度，引入边界条件后，无限长Euler梁被简化为有限长简支梁；轨道板在垂向按弹性地基上的等厚矩形薄板考虑，而横向则考虑为刚体。钢轨、轨道板、桥面之间通过线性弹簧和阻尼元件连接。轨道子系统的运动方程为

(2)

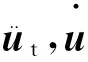
2.3桥梁动力学模型

桥梁动力学模型采用空间杆系有限元建模。其中，主梁和桥塔采用空间梁单元模拟；斜拉索采用空间杆单元模拟，斜拉索因自重垂曲引起的非线性效应(采用Ernst公式)通过折减其弹性模量来考虑；恒载初始内力对结构刚度的影响通过在杆单元刚度矩阵上叠加几何刚度矩阵实现。

墩梁之间的联结采用主从关系模拟，承台底采用刚性约束，桥面二期恒载按均布质量分配到主梁单元。建立的桥梁子系统运动方程为

(3)

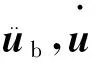
2.4轮轨、桥梁相互作用关系

轮轨关系是车辆子系统与轨道子系统联系的纽带，包括轮轨接触几何关系和轮轨间力的关系，计算中假设轮轨刚性接触，并允许发生脱离，其法向接触力采用Hertz非线性弹性接触理论求解，切向力采用Kalker线性蠕滑理论求解，并通过Johnson-Vermeulen理论进行非线性修正。桥轨关系是联系桥梁子系统与轨道子系统的纽带，包括轨道板与桥梁之间的几何相容和静力平衡条件。计算中轨道板位移通过桥梁节点位移插值得到，并由轨道板位移求出作用在其上的横向力和垂向力。轮轨和桥轨关系确定之后，即可由式(1)～(3)通过数值积分求得各子系统的动力响应[13-14]。

3　算例

3.1计算条件

以某(60.5+156+464+156+60.5)m五跨连续钢桁梁铁路斜拉桥为工程背景，主桥采用半漂浮体系，斜拉索从左至右依次编号为1～28(左半跨)。在不考虑斜拉索局部振动的单桁架模型(SECS)的基础上，将每根斜拉索划分为15个杆单元，得到了考虑斜拉索局部振动的多桁架模型(MECS)，见图3。

图3　考虑斜拉索局部振动MECS模型Fig.3 MECS model

采用子空间迭代法计算了两种模型的自振特性，图4给出了MECS模型的典型振型图，同时表1给出了SECS、MECS两种模型的主要自振频率与振型。

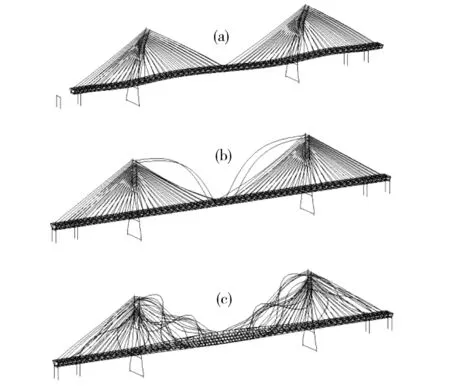
(a)主梁纵漂振型；(b)拉索振型；(c)索桥耦合振型图4　MECS模型典型振型图Fig.4 Typical modals of MECS model

由表1可见，SECS和MECS两种模型前三阶振型均为主梁振动，在MECS模型中，从第四阶振型开始，出现了包含拉索振动的振型，延迟了主梁和桥塔振型的出现。

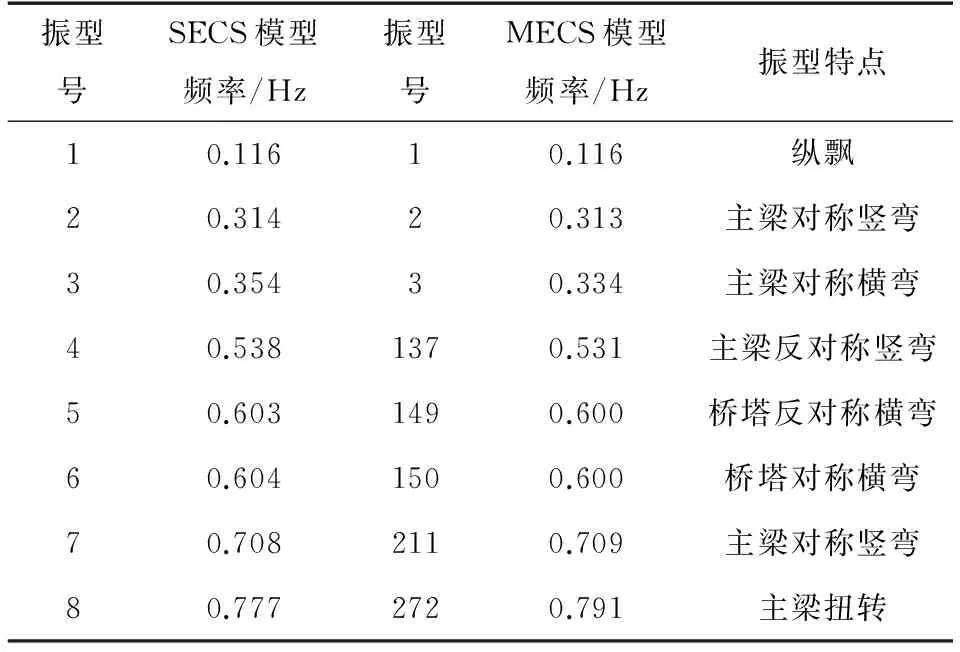
表1　结构主要自振频率及振型

图5给出了MECS模型斜拉索前三阶频率分布图。由图5可见，主梁一阶纵飘频率低于所有拉索的一阶自振频率，导致MECS模型第一阶振型仅出现桥梁的纵飘而未出现拉索的振动，与图4(a)中显示一致；而主梁对称扭转频率为0.777 Hz，与4,13,23,24和25号索的频率0.799 7，0.748，0.799 3，0.770 5和0.756 3 Hz接近，在MECS模型第272阶振型中出现了以上五根索局部的振动，与图4(c)中显示结果一致。可以得出：当斜拉索频率与主梁结构频率接近时，会产生拉索的局部振动，出现索桥耦合振动的可能增大，进而可能加剧桥梁、车辆的动力响应。

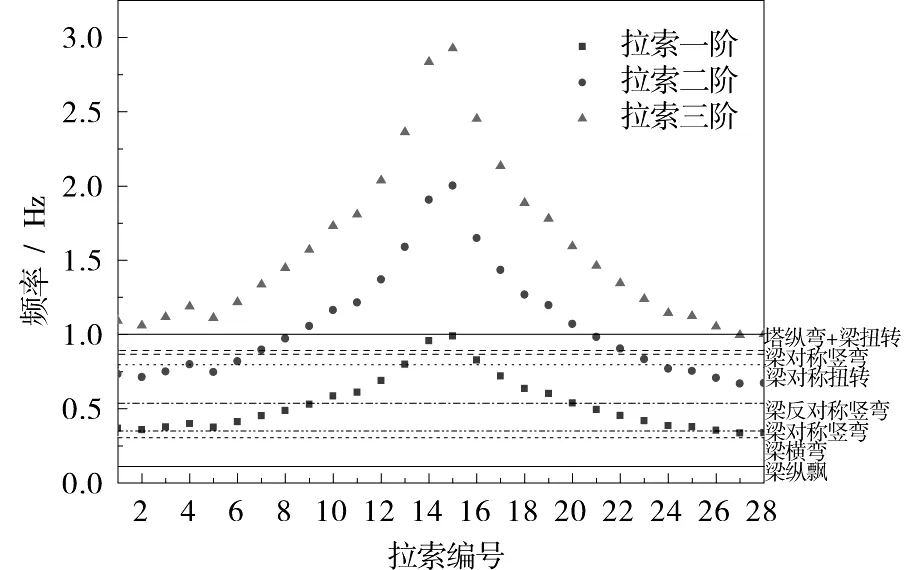
图5　桥梁主要振型及斜拉索自振频率分布图Fig.5 Frequency range of cable and typical modals of bridge

在进行车桥耦合动力仿真分析时，采用地铁B型车，车辆参数见文献[10]，速度等级采用50,70,90,120和150 km/h，轨道不平顺采用美国六级谱。针对上述SECS和MECS两种模型，使用自主研发的桥梁动力分析程序BDAP v2.0进行列车-桥梁空间动力仿真计算。

3.2桥梁动力响应

针对SECS和MECS两种模型，选取主梁跨中、塔顶节点为研究对象，可以得到桥梁关键节点的位移响应。图6给出了设计时速为120 km时，主梁跨中节点横向、竖向的位移时程曲线，表2给出了不同车速下主梁跨中节点的加速度响应幅值。

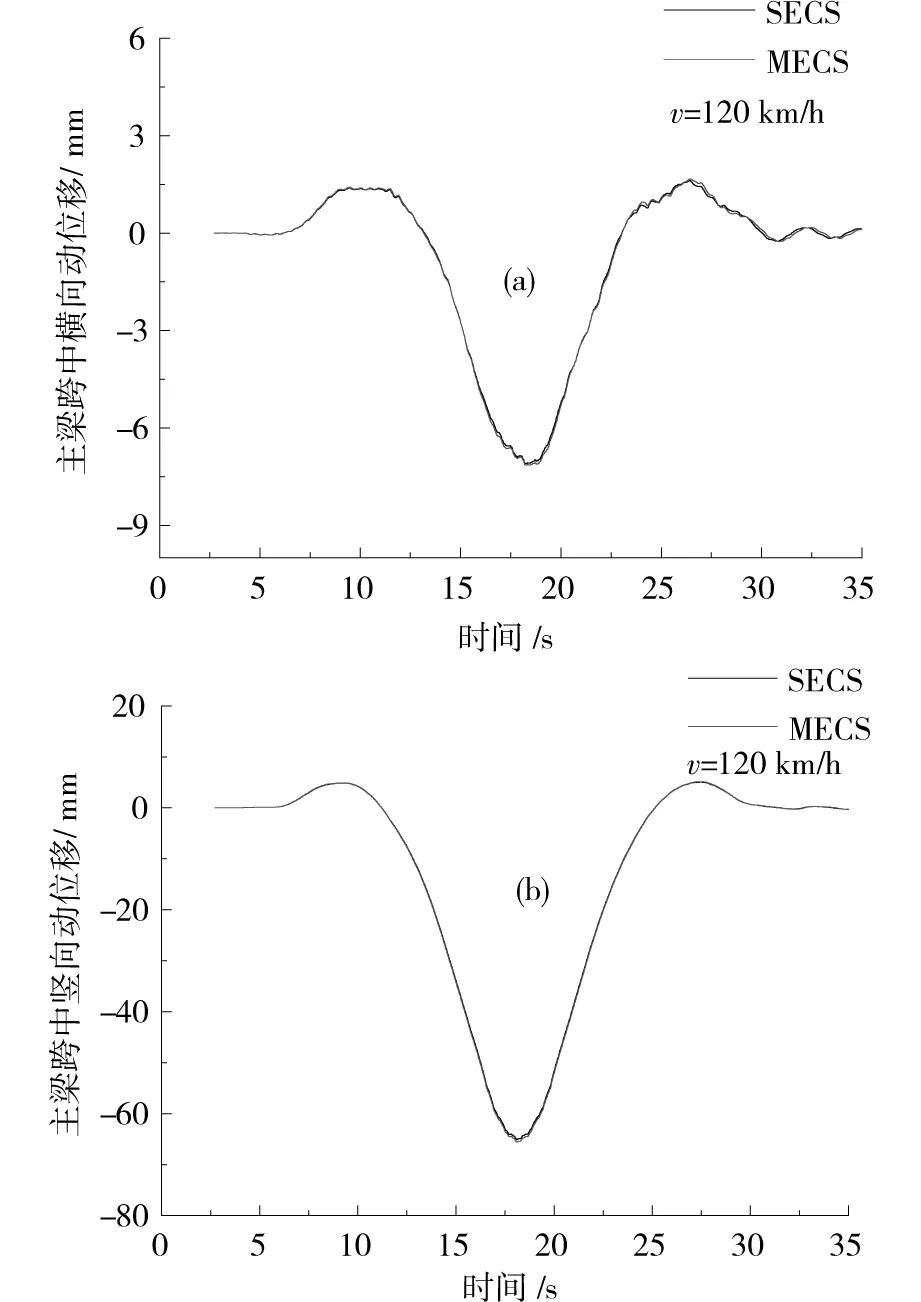
图6　桥梁跨中位移时程曲线Fig.6 Dynamic displacement of bridge

由图6可见，考虑拉索局部振动后，桥梁横向位移、竖向位移时程曲线变化不大，动位移响应幅值差别不大。说明桥梁跨中位移受拉索局部振动的影响有限。相对SECS模型，MECS模型桥塔顶端纵向、横向位移均有小幅减小，减小幅度分别为1%和3%。

由表2可见，不同模型下桥梁跨中节点的加速度响应差异显著。MECS模型中桥梁跨中横向加速度幅值总体偏大，与SECS模型相比，最大增幅发生在速度为50 km/h时；考虑拉索局部振动后，桥梁跨中竖向加速度响应值较单桁架模型有少量减小，减小幅度一般在5%之内。

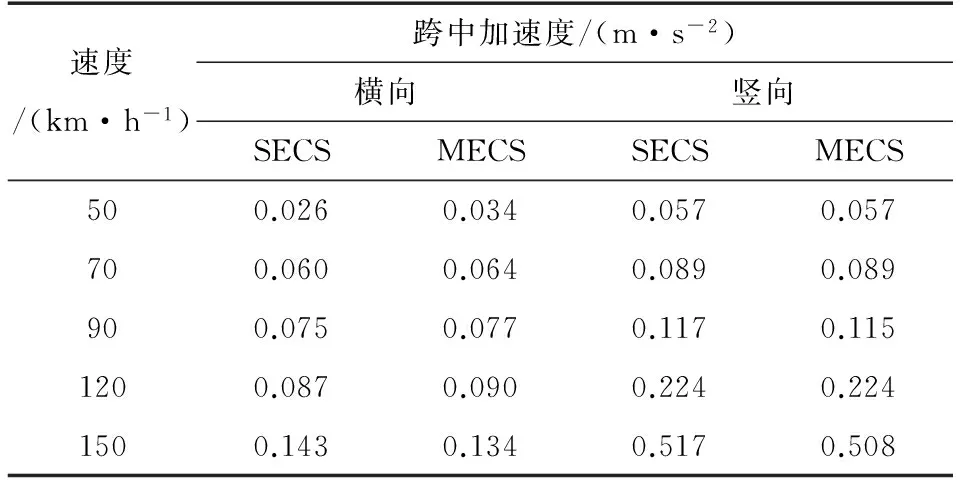
表2　桥梁跨中节点加速度响应对比

图7给出了速度为50 km/h时，两种模型主梁跨中的横向加速度时程对比曲线。可以看出，不考虑拉索局部振动(SECS模型)会低估主梁跨中的横向加速度响应。

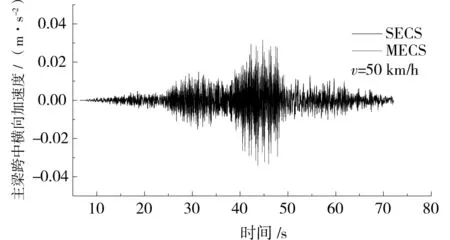
图7　桥梁跨中横向加速度时程曲线Fig.7 Dynamic lateral acceleration of bridge

表3列出了不同车速下SECS和MECS两种模型塔顶节点的加速度响应幅值，图8给出了部分速度下塔顶纵向、横向加速度响应时程图。由表3和图8可见，在考虑拉索局部振动的MECS模型中，塔顶加速度有明显减小。这是因为考虑斜拉索局部振动后，拉索的振动与桥塔的振动未能完全同步，对桥梁结构来说产生了附加阻尼，削弱了斜拉桥塔顶的动力响应。

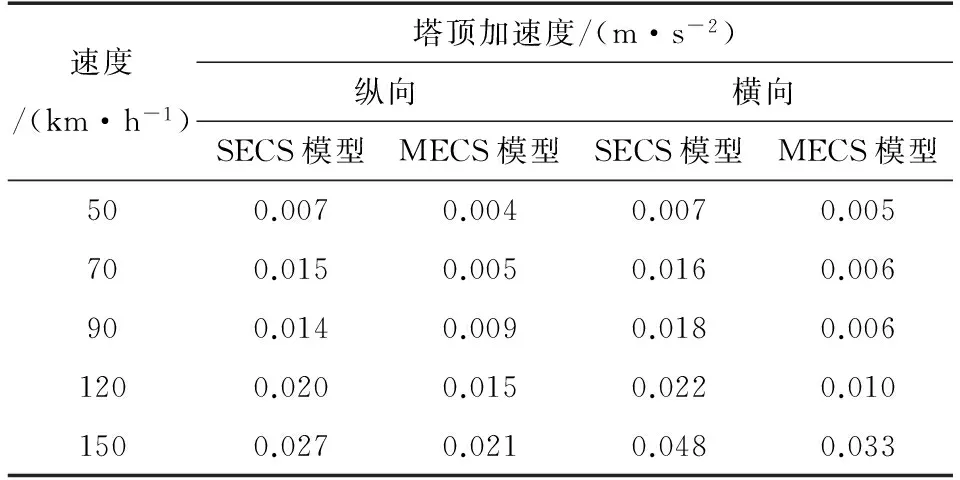
表3　斜拉索局部振动对塔顶加速度影响

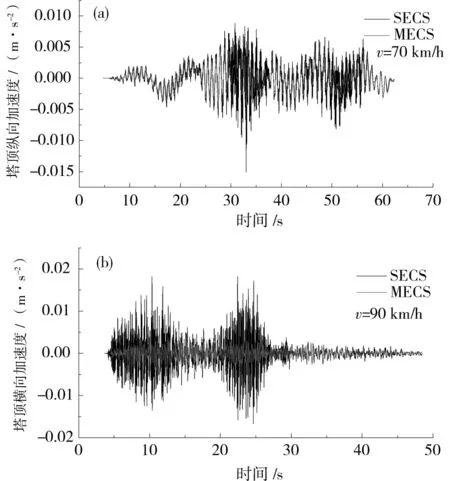
图8　塔顶加速度时程曲线Fig.8 Dynamic acceleration of pylon

3.3车辆动力响应

限于篇幅，这里仅给出多桁架模型(MECS模型)在不同计算车速下的车辆动力响应幅值，见表4所示。

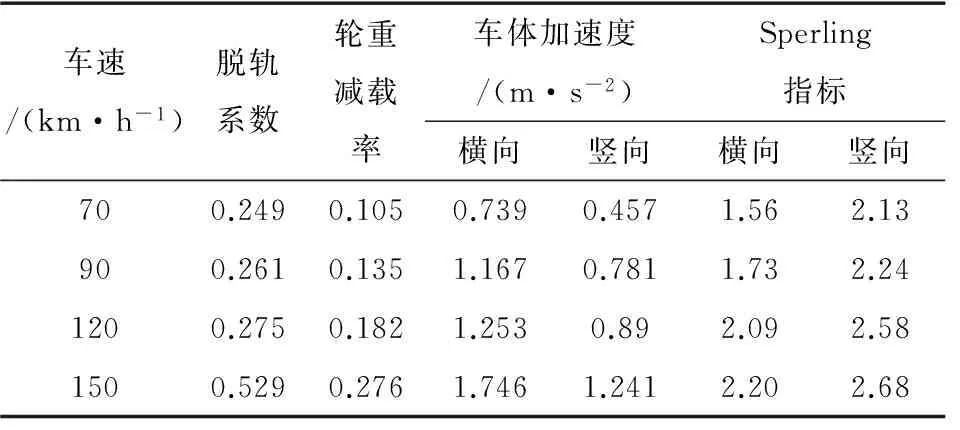
表4　MECS模型车辆动力响应

根据《铁道机车动力学性能试验鉴定方法及评定标准》规范，在120 km设计时速下，车辆的脱轨系数小于容许值0.8，轮重减载率小于容许值0.6；车体加速度、Sperling指标均未超限，车辆的安全性得以保障，舒适性达到良好。

对比SECS和MECS两种模型的车辆响应结果可以发现，不考虑拉索的局部振动时列车的脱轨系数、轮重减载率、摇摆力、车体加速度以及Sperling指标均没有显著变化。从上节可以看出，拉索局部振动对桥梁位移影响较小，相应的，通过线桥关系传递给轨道的振动也较弱，进而无法影响到车辆的安全性和舒适性指标。

4　结论

1)斜拉索局部振动对斜拉桥的动力特性有较大影响。考虑斜拉索局部振动后，出现了大量纯索振动振型与索-梁耦合振型；

2)斜拉索局部振动对斜拉桥关键部位的加速度响应影响显著。本文算例中斜拉桥跨中横向加速度有小幅增大而塔顶纵向、横向加速度有明显减小。

3)车桥耦合分析时，桥上车辆响应受斜拉索局部振动影响较小，原因是拉索局部振动对桥梁位移影响小，通过线桥关系传递给轨道的振动弱，进而无法明显影响到车辆的安全性、舒适性指标。

[1] Abdel-Ghaffar, Khalifa M A. Importance of cable vibration and dynamic cable-stayed bridges [J]. Journal of Engineering Mechanics-ASCE, 1991, 117(11): 2571-2589.

[2]PACHECO B M, FUJINO Y. Keeping cables calm [J]. Civil Engineering, 1993, 63(10): 56-58.

[3] YANG Fuheng, FONDER G A. Dynamic response of cable-stayed bridges under moving loads [J]. Journal Engineering Mechanics, 1998, 124(7): 741-747.

[4] 亢战，钟万勰. 斜拉桥参数共振问题的数值研究[J]. 土木工程学报，1998, 31(4): 14-22.

KANG Zhan, ZHONG Wanxie. Numberial study on parametric resonance of cable in cable stayed bridge [J]. China Civil Engineering Journal, 1998, 31(4): 14-22.

[5] 王涛，沈锐利，李洪. 斜拉桥索-梁相关振动概念及其研究方法初探[J]. 振动与冲击. 2013, 32(20): 29-34.

WANG Tao, SHEN Reili, LI Hong. Primary exploration for concept and studying method of cable-beam vibration in a cable-stayed bridge [J]. Journal of vibration and shock, 2013, 32(20): 29-34.

[6] 张鹤，谢旭. 车辆荷载作用下大跨度斜拉桥钢和CFRP拉索的非线性振动[J]. 工程力学,2009, 26(8): 123-130.

ZHANG He, XIE Xu. Nonlinear vibration of steel and CFRP cables of long span cable-stayed bridge under vehicular loads [J]. Engineering Mechanics, 2009, 26(8): 123-130.

[7] 苗永抗，郭向荣，何旭辉. 钢-混结合对列车与混合梁斜拉桥耦合振动的影响分析[J]. 铁道科学与工程学报, 2013,12(6): 14-20.

MIAO Yongkang, GUO Xiangrong, HE Xuhui. Analysis of the influence of steel-concrete joint section on coupling vibration of vehicle and cable-stayed bridge with hybrid girder [J]. Journal of Railway Science and Engineering, 2013, 12(6): 14-20.

[8] 尹邦武，苗永抗，郭向荣. 斜拉-连续刚构组合梁桥车-桥耦合动力响应分析[J]. 铁道科学与工程学报, 2013, 02: 11-17.

YIN Bangwu, MIAO Yongkang, GUO Xiangrong. The vehicle-bridge coupling dynamic analysis of cable-stayed and continuous rigid-frame composite beam bridge [J]. Journal of Railway Science and Engineering, 2013, 10(2): 11-17.

[9] 李小珍，强士中，沈锐利. 高速列车-大跨度钢斜拉桥空间耦合振动响应研究[J]. 桥梁建设,1998(4): 67-70.

LI Xiaozhen, QIANG Shizhong, SHEN Ruili. Studies on space dynamic responses of high speed train-long span steel cable-stayed bridge [J]. Bridge construction, 1998(4): 67-70.

[10] 李小珍，强士中. 大跨度公铁两用斜拉桥车桥动力分析[J]. 振动与冲击,2003, 22(1): 8-11.

LI Xiaozhen, QIANG Shizhong. Vehicle-bridge dynamic analysis for long span highway and railway Bi-purpose cable-stayed bridge [J]. Journal of Vibration and Shock, 2003, 22(1): 8-11.

[11] 王刚，曹雪琴. 高速铁路大跨度斜拉桥车桥动力分析[J]. 上海铁道大学学报. 2000, 21(8): 7-11.

WANG Gang, CAO Xueqin. Dynamic analysis of long-span cable-stayed bridge under the high-speed train[J]. Journal of Shanghai Tiedao University, 2000, 21(8): 7-11.

[12] 翟婉明，夏禾. 列车-轨道-桥梁动力相互作用理论与工程应用[M]. 北京：科学出版社, 2011.

ZHAI Wanming, XIA He. Train-track-bridge dynamic interaction theory and engineering application [M].Beijing: Science Press, 2011.

[13] 李小珍. 高速铁路车辆-桥梁耦合振动理论与应用研究[D]. 成都: 西南交通大学, 2000.

LI Xiaozhen. Studies on theory and application of train-bridge system coupling vibration in high-speed railway [D].Chengdu: Southwest Jiaotong University, 2000.

[14] 雷虎军，李小珍. 车-轨-桥耦合系统中的非一致地震输入方法研究[J]. 铁道科学与工程学报, 2015, 12(4): 769-777.

LEI hujun, LI Xiaozhen. Input methots of non-uniform seismic excitation in coupling system of vehicle-track-bridge [J].Journal of Railway Science and Engineering, 2015, 12(4): 769-777.

Analysis of bridge and vehicle coupled vibrations with cable vibration

LEI Hujun1，LI Wenqiu2，LI Xiaozhen2

(1．College of Civil Engineering, FuJian University of Technology, Fuzhou 350118, China;2．School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

In order to study the influence of cable vibration on the responses of train and cable-stayed bridge system, the MECS model through considering the cable vibrations and the traditional SECS model were set up based on the cable-bridge interaction theory, respectively. As an example, a five continuous steel truss beam railway cable-stayed bridge with spans of 60.5+156+464+156+60.5m was modeled, and the responses of vehicle and bridge system under B-type subway body running over the bridge at different speeds were calculated and compared by the version 2.0 of bridge dynamic analysis program (BDAP V2.0). The results show that a large number of single cable vibration mode and cable-beam coupled vibration mode appear after considering the cable vibration, and the cable vibration has trivial influence on the dynamic responses amplitudes of the train. If the cable vibration of the cable-bridge model are ignored, the acceleration responses of the tower on the top may be overrated. So, the cable vibration should not be ignored when the dynamic responses of long span cable-bridge are analyzed.

vehicle-bridge coupled vibration; cable-stayed bridge; cable vibration; multiplier-element cable system

2015-12-25

福建省教育厅中青年教师教育科研资助项目(JA15333)；校科研启动基金资助项目(GY-14077)

雷虎军(1986-)，男，四川渠县人，讲师，博士，从事桥梁结构抗震与车-桥耦合振动研究；E-mail：leihujun@yeah.net

U24；TB123

A

1672-7029(2016)09-1756-06