大吨位压路机碾压大粒径填石路基的动力响应

金书滨,张长胜,刘政,乔世范

(1．贵州省公路工程集团有限公司，贵州 贵阳 550008；2.中南大学 土木工程学院，湖南 长沙 410075)



大吨位压路机碾压大粒径填石路基的动力响应

金书滨1,张长胜2,刘政1,乔世范2

(1．贵州省公路工程集团有限公司，贵州 贵阳 550008；2.中南大学 土木工程学院，湖南 长沙 410075)

采用动土压力盒测量盘兴高速公路三标和四标试验段大吨位压路机碾压试验时的动土应力，进行大粒径填石路基的动力响应分析。依据应力波在竖向的衰减规律，得出碾压动应力值的衰减函数；使用简化模型分析振动碾压时路基的压实作用，有限元软件计算结果和试验数据验证了模型的准确性；依据不同施工条件下的动土应力值，得出最佳施工参数，碾压遍数不低于8遍，最佳摊铺厚度为100 cm，最大粒径控制为50 cm，压路机最大激振力80 t，在此施工条件下可有效提高路基碾压的施工质量。

振动压实; 大粒径填料; 填石路基; 动力响应

近年来，大量工程实践表明大吨位压路机碾压大粒径路基有显著的经济效益和压实效果。振动压路机压实机理[1]是其振动器在平衡位置来回作用，从而产生强大的冲击力作用于路基面上；路基填料受冲击波[2-5]的作用克服了摩擦力和惯性力，使小颗粒填料不断填充到大粒径填料空隙中，颗粒间的空隙率不断减小，填料在荷载影响下重新分布，从而提高了填石路基的压实质量。振动压路机压实路基时，填料受冲击波作用获得相应的振动频率，冲击能随深度方向逐步递减。影响路基压实质量因素[6]较多：激振力、振动作业次数、碾压层厚、粒径。

80年代初，我国开始修筑粗颗粒填石路基，但对路基填料的施工工艺、质量检测的研究都是基于细填料基础上。近年来，通过工程实践、现场试验和理论研究，在粗填料碾压技术上取得了一定的成果[6]。国外学者对粗颗粒路基施工进行了大量的研究[7-9]，英国运输部针对粗填料和填土石进行了分类；澳大利亚在路基施工中控制大粒径填料直径为25 cm；日本在粗填料和填土石施工作业中采用了质量和施工工艺控制。

盘兴高速公路施工中将山区挖方碎石料作为路基填料以便减少施工成本。碎石料可作为良好的路基填料，具有强度高、工后沉降小、压实效果好等工程特征[10]。山区高速公路施工最大粒径和摊铺厚度的控制往往依据经验确定，缺乏研究[11]。为确保施工质量，检测大粒径路基碾压压实效果，拟进行大粒径填石路基的动力响应分析，以便有效指导大粒径填石路基作业和提高路基压实质量，对此类施工作业和质量控制提供参考。

1　动土压力盒的测试方案

现场试验区段为贵州盘兴高速公路三标段k52+636 ～ k52+664和四标段k80+320 ～ k80+340。三标段和四标段填料分别为灰岩、红砂岩，路基填方面积大，石料强度高。

因为现场的填料主要为大粒径的碎石，本试验选用的动土压力盒为双模电阻应变式，最大测量值为600 kPa。碾压试验采取分层碾压法，并且每层至少埋设一个动土压力盒。为了获取合适的摊铺厚度，首先第一层严格按照规范规定的80 cm为一层，上面三层的摊铺厚度分别为100,120,150和200 cm。图1为动土压力盒埋设示意图。把最下面一层严格按照现行规范进行施工，认为压实质量是达到要求的，定义为标准层。试验过程中上面几层的压实后所测得的动土压力与标准层的动土压力进行对比，以评价不同的摊铺厚度的压实效果。由于碾压试验有多组对比试验，不同断面的动土压力盒埋设和摊铺厚度不同，为保证动土压力盒测量准确和周围石料不产生土拱效应。需确保动土压力盒埋设水平，压力盒上部和下部需铺撒5 cm左右的细料，动土压力盒测试线由旁边引出，并用细料掩埋。

图1　仪器布置示意图Fig.1 Instrument layout

现场采用东华DH5937采集仪和DHDAS测试系统测量大粒径填石路基的动土应力值。试验采用大吨位压路机的型号为Y-21、XG-626M，最大激振力分别为80 t和60 t。

2　碾压动力响应分析

2.1动应力随碾压遍数的变化规律

压路机型号为Y-21，试验断面为四标k80+340，摊铺厚度为1.0 m，最大粒径为65 cm。动土应力值变化规律如图2所示。

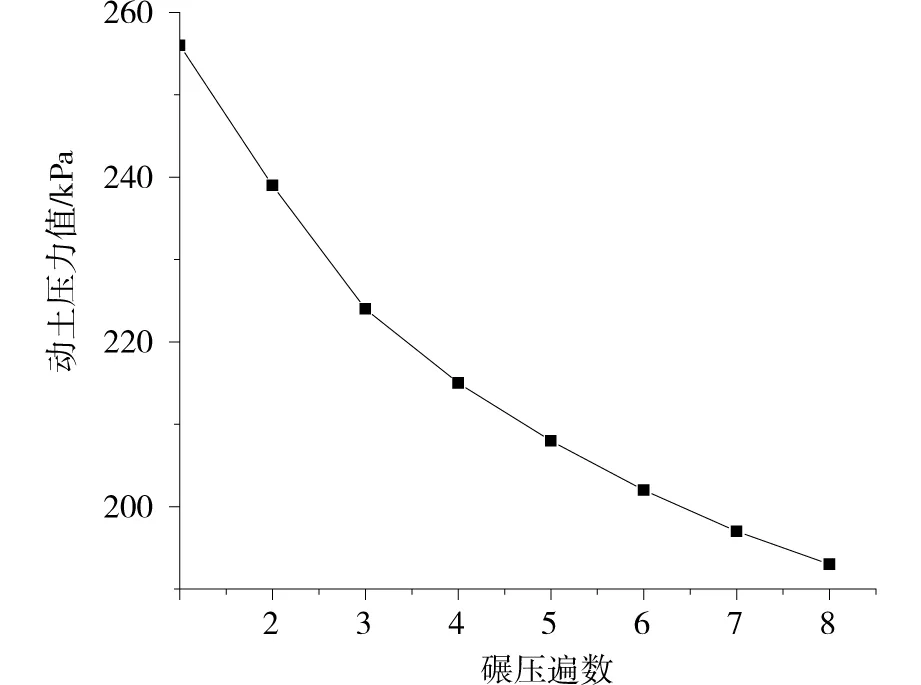
图2　动土应力峰值与碾压遍数的关系Fig.2 Relationship between the dynamic earth stress and the times of rolling

试验结果表明，碾压遍数为1-3遍时，动土应力值衰减呈线性变化，动土应力值由260 kPa下降到224 kPa；碾压作业4-6遍时，应力值变化较缓慢；碾压作业7-8遍时，应力值趋于平缓，应力值增加量可忽略。分析发现继续振动压实作业，应力值呈减小趋势，在施工作业为7-8遍时趋于稳定。曲线变化规律间接表明随着冲击波的作用，大颗粒间的空隙被细颗粒填充，颗粒间振动受到的约束逐渐增大，填料的压实质量提高明显，在振动碾压作业8遍后，路基的压实质量趋于稳定。

2.2不同施工参数下动土应力变化规律

本试验采用压路机型号为Y-21，XG-626M，试验区段为盘兴高速三标、四标。试验数据显示，当摊铺厚度大于150 cm，动土应力值已经不明显，所以试验数据中未统计摊铺层200 cm的动土应力值，试验数据如表1所示：

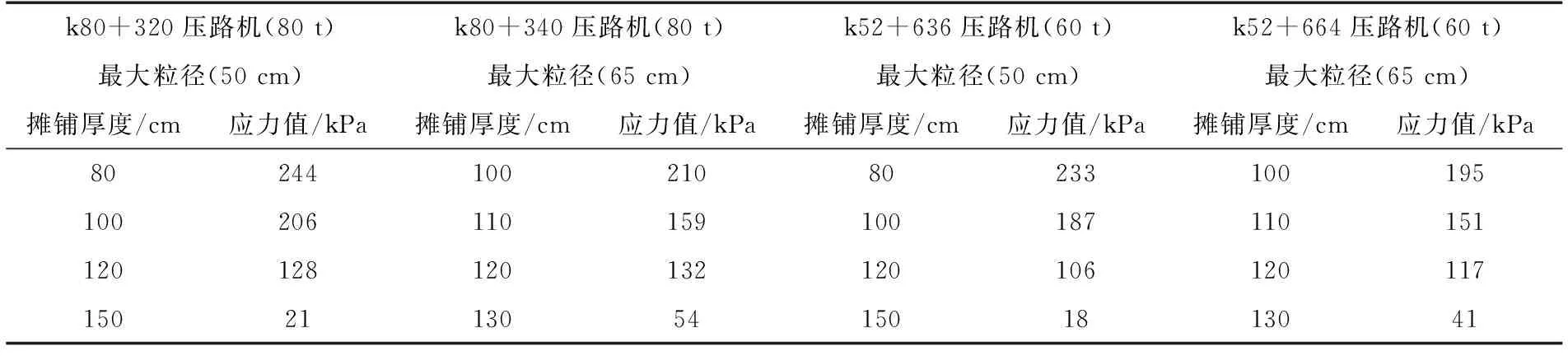
表1　不同条件的动土应力值统计

2.2.1动土应力值随摊铺厚度变化

试验数据显示摊铺厚度为80cm时，动土应力值大于230kpa；摊铺厚度大于100cm时，动土应力值发生明显的衰减。结合试验断面K80+320和试验断面K52+636数据分析：当摊铺厚度由80cm增加到100cm时，动土应力值衰减明显，动土应力值降低了15.6%和19.7%；当摊铺厚度增加到120cm时，动土应力值降低非常明显，此时动土应力值占最大值的52.5%和45.5%。试验断面K80+340和试验断面K52+664数据分析：当摊铺厚度由100cm增加到110cm时，动土应力值降低了24.3%和22.6%；当摊铺厚度增加到120cm时，此时动土应力值占最大值的62.9%和60%，以上数据表明大粒径填石路基的摊铺厚度不易大于100 cm，同时不应大于120 cm。

2.2.2最大粒径变化对动土应力值影响

在摊铺层100cm，最大粒径65 cm时，试验测得动土应力值为210和195kPa；而最大粒径为50cm时，测得应力值为206和187kPa。动土应力值降低了1.9%和4.1%。摊铺厚度为120cm时，最大粒径由65cm减小到50cm，动土应力值降低了3.1%和9.4%。试验结果表明最大粒径越小，动土应力值越小。动土应力值越小间接反应填料间约束力越大，其压实效果越好。

2.2.3压路机吨位对动土应力值的影响

摊铺厚度为100cm，压路机最大激振力为60 t时，测得动土应力值为187和195kPa；压路机最大激振力为80t时，测得动土应力值为206和210kPa，动土应力值增加了10.2%和7.7%；摊铺厚度为120cm时，增大压路机激振力，动土应力值分别增加了20.8%和12.8%。研究表明增加压路机最大激振力，可显著提高压路机对路基的冲击能，改善路基的压实效果。

2.3不同深度下动土应力变化规律

2.3.1现场试验数据

本试验采用压路机型号为XG-626M，试验区段为三标k52+664断面。为更好分析动土应力随深度的变化规律，在不同摊铺层埋设动土压力盒，其中第一层埋设了7个动土压力盒，其余各层埋设1个动土压力盒，动土压力盒埋设深度为0.5，0.8，1，1.2，1.5，1.8，2，3.3，4.5，5.5和6.3 m。碾压后测量的动土应力值如表2所示。

分析表2试验数据，在深度为0.5 m时测得动土应力最大值为347 kPa；深度为1.2 m时，动土应力值为122 kPa，占最大测量值的35.2%；1.5 m时动土应力值衰减到78 kPa，占最大测量值的22.5%；深度为2 m时，动土应力值衰减到37 kPa，占最大测量值的10.6%。研究表明深度小于1.2 m时，测量的动土应力值比较明显，占最大测量值的35%，试验表明压路机振动产生的冲击能随深度方向衰减很快。

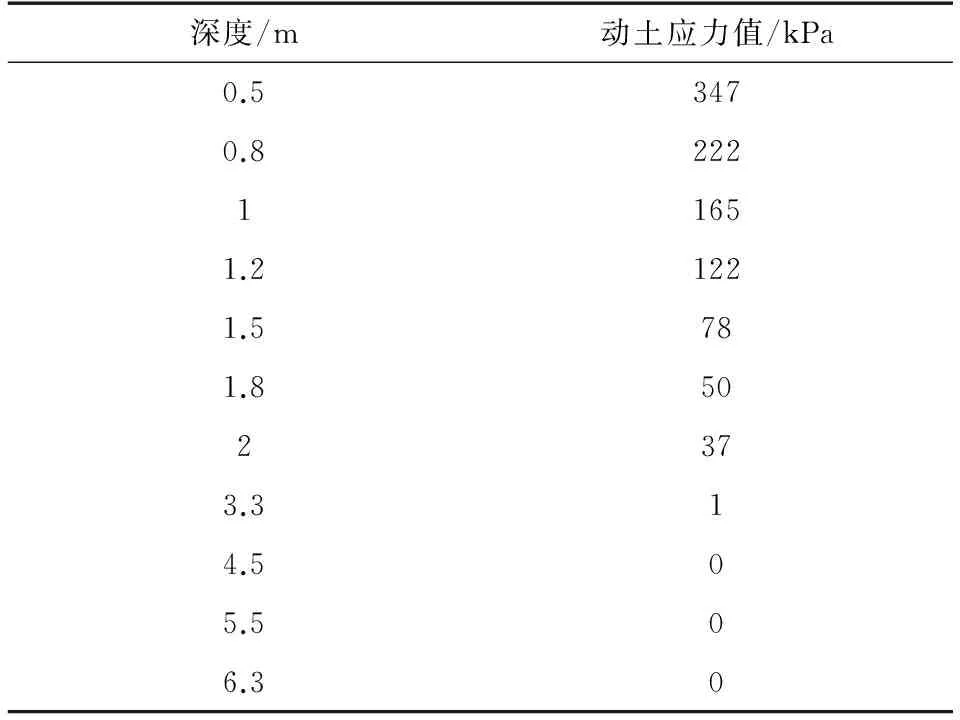
表2　动土应力随深度变化

2.3.2振动压实机理和动应力衰减

振动压实过程中，路基填料受振动作用获得振动加速度：

(1)

压路机获得的额外作用力为：

I=-mAω2cos(ωt+β)

(2)

压路机对地面作用荷载为：

(3)

式(3)中：A为振幅；ω为振动频率；β为相位角；t为时间；m为压路机质量。

压路机对地面作用的最大荷载为：

F=G+I=mg+mAω2

(4)

假定在Δt作用时间内，压路机对地面作用力均匀分布在宽度为L的区间上，压路机行驶速度为V，压路机作用效果可简化如图3所示：

图3　碾压简化模型Fig.3 Simplified model of rolling

压路机对路基作用最大初始应力为：

(5)

压路机振动施工作业时，产生周期荷载作用于压实路基，每个周期荷载作用于路基填料时，填料中就产生一个冲击波，冲击波将随着填料在深度方向传递和扩散。参考相关文献，冲击波在土体中衰减呈指数衰减，不同深度下的动应力幅值为：

(6)

式中：H为测点距震源的垂直距离；σd0为初始动应力；K为动应力衰减系数。

压路机碾压施工时，应力波在同一填料的传播过程中，其碾压速度和碾压频率都不会改变，即σd0大小不变。综合以上式子和原理得到动应力值和深度之间的关系：

σdmax=σd0e-kh

(7)

图4的曲线显示，动土应力值在竖向衰减很快。分析动土应力值和深度之间的拟合曲线，相关性系数R2为0.981，相关性非常好。结果表明动土应力值衰减规律和公式(7)符合，碾压时动土应力值衰减呈指数衰减。

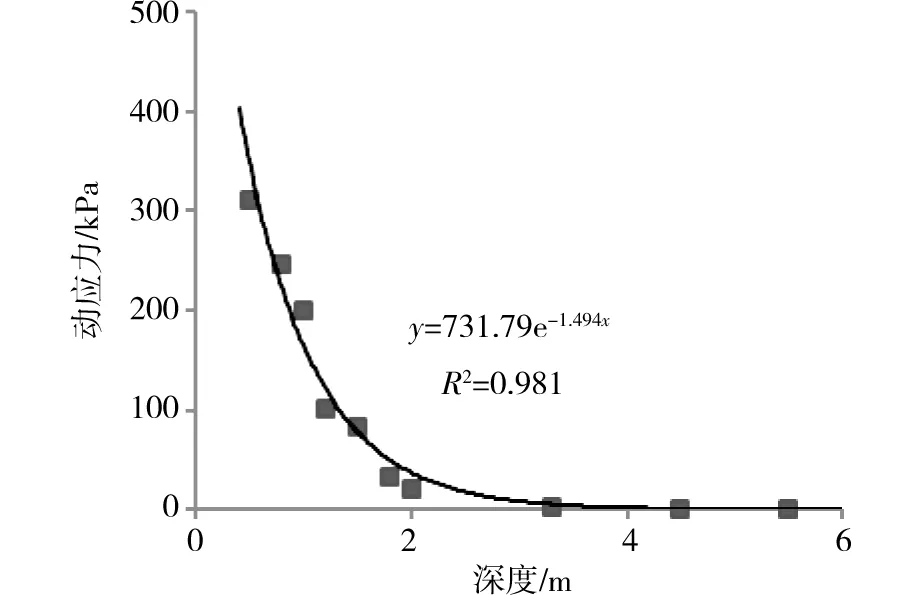
图4　动应力与深度的关系Fig.4 Relationship between dynamic stress and depth

3　碾压压实有限元简化计算

3.1简化原理

依据图3简化模型，将压路机匀速施工作业，简化为在质点受三角形周期冲击荷载的作用，其中长度为L，宽度为vt，为保证计算结果的准确性，vt应小于压路机振动轮宽度，T为一个振动周期，作用总时间为t，如图5所示：

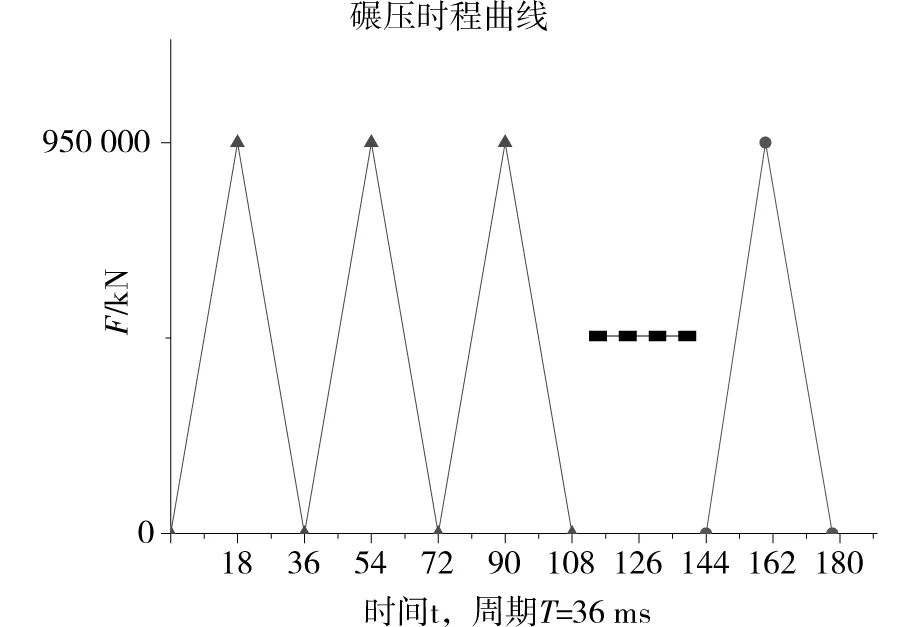
图5　碾压等效荷载Fig.5 Equivalent load of rolling

其中

(8)

(9)

受冲击力作用路基结构的力学分析为：

(10)

使用Rayleigh阻尼分析计算，由式(10)可得：

(11)

(12)

由(12)式可得：

(13)

(14)

为简化书写引入相关符号：

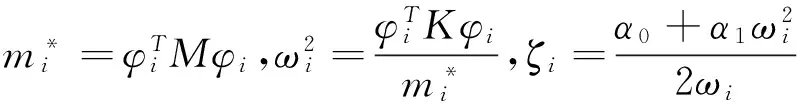
则式(14)简化为:

(15)

求解路基结构的力学方程得到：

(16)

3.2ABAQUS有限元分析验证

使用ABAQUS软件分析碾压试验过程，压路机最大激振力为60 t，采用Drucker Prager计算模型，计算参数如下表3所示，图6为有限元计算模拟的应力图：

表3　碾压有限元计算参数

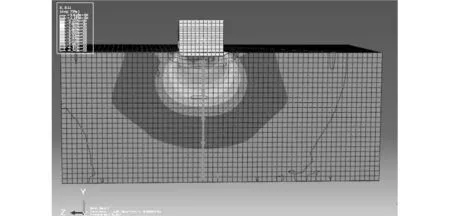
图6　碾压竖向应力图Fig.6 Rolling vertical stress diagram

通过ABAQUS模拟压路机碾压试验，应用有限元软件计算出动土应力值，分析压路机正下方动应力值，如图6路径所示。图7为有限元计算动土应力值与试验值分析对比。

对比有限元计算出的数据和实测数据，研究表明通过简化模型计算出的碾压动土应力值衰减变化规律和实测值吻合，可用简化模型分析碾压时的受力情况。

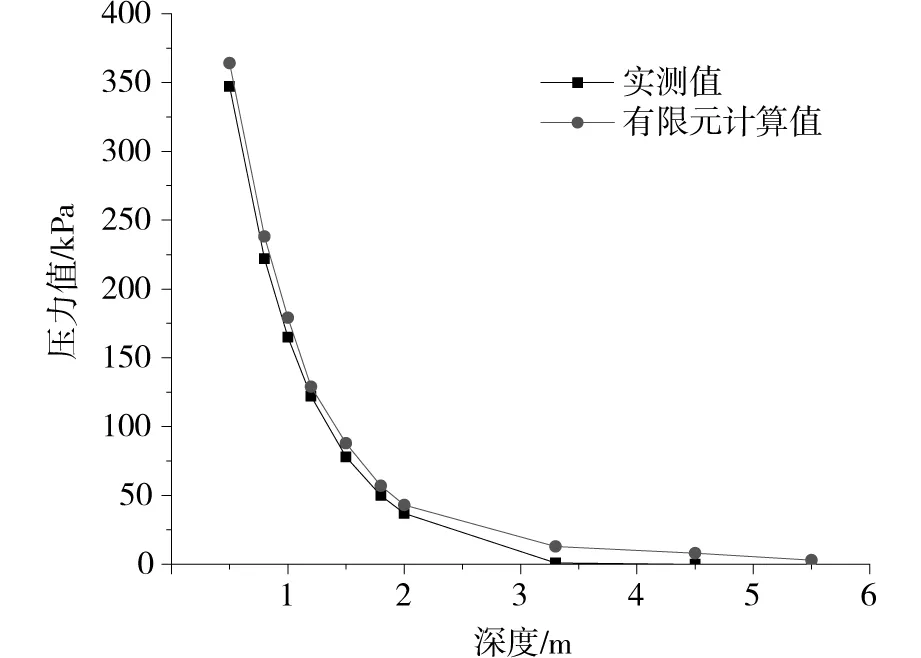
图7　计算和实测动土应力随深度方向变化Fig.7 Calculated and measured stress with depth direction changes

4　结论

1)依据动土应力值的变化规律，填石路基最佳碾压遍数不宜低于8遍；大粒径填石路基最佳摊铺厚度为100 cm，最大摊铺厚度不大于120 cm；最大粒径越小，填石路基的压实效果越好，最大控制粒径为50 cm；提高压路机激振力能显著提高振动冲击能，确保压实质量。

2)依据应力波在竖向衰减规律，对试验数据进行了回归分析得到动应力值衰减函数，相关线性系数R2为0.981。

3)对压路机施工作业过程进行了力学简化，分析了填石路基受力情况。使用有限元软件ABAQUS进行动力响应分析，结果验证了简化模型的可靠性。

[1] 贾莉浩.高速铁路高填方路基粗颗粒填料关键技术研究[D].长沙：中南大学, 2013.

JIA Lihao. Research on the key technology of coarse-grained filler in high embankment of the high-speed railway [D]. Changsha: Central South University, 2013.

[2] 陈涛,但汉成. 高填方土石混填路堤冲击碾压试验研究[J]. 铁道科学与工程学报, 2014, 11(1): 101-105.

CHEN Tao, DAN Hancheng. Experimental study of impact rolling technology of high subgrade filled with soil and rock [J]. Journal of Railway Science and Engineering, 2014, 11(1): 101-105.

[3] Sitharam T G, Nimbkar M S. Micromechanical modelling of granular materials: effect of particle size and gradation[J]. Geotechnical and Geological Engineering, 2000, 18(2): 91-117.

[4] 窦鹏,聂志红,王翔. 铁路路基压实质量检测指标CMV与Evd的相关性校检[J]. 铁道科学与工程学报, 2014, 11(2): 90-94.

DOU Peng，NIE Zhihong，WANG Xiang. Correlation verification of railway subgrade compaction quality test value between CMV and Evd[J]. Journal of Railway Science and Engineering, 2014, 11(2): 90-94.

[5] 胡昌斌, 袁燕. 冲击碾压改建路面施工对路基动力作用的试验研究[J]. 岩土力学, 2011, 32(3): 745-752.

HU Changbin, YUAN Yan. Dynamic soil pressure characteristics of embankment under impact rolling load during rehabilitation of PCCP[J]. Rock and Soil Mechanics, 2011, 32(3): 745-752.

[6] 石云, 郑月秀. 大粒径填石路堤碾压试验研究[J]. 公路交通技术, 2011(6): 13-15.

SHI Yun, ZHENG Yunxiu. Experimental research on rolling compaction of large particle size rock filling roadbed[J]. Highway and Transport, 2011(6): 13-15.

[7] YANG S J. Impact compaction of coarse-grained soil subgrade[J]. Journal of Highway and Transportation Research and Development, 1999, 16(1): 1-6.

[8] LIU D, LIN M, LI S. Realtime quality monitoring and control of highway compaction[J]. Automation in Construction, 2016(62): 114-123.

[9] Kenneally B. Finite element analysis of vibratory roller response on layered soil systems[J]. Computers & Geotechnics, 2015(67): 73-82.

[10] 许锡昌,周伟,韩卓,等. 土石混合料的压实特性研究[J]. 岩土力学, 2010, (S2): 115-118.

XU Xichang, ZHOU Wei, HAN Zhuo, et al. Research on compaction properties of soil-aggregate mixture, Rock and Soil Mechanics, 2010, (S2): 115-118.

[11] 陈爱军, 张家生, 贺建清,等. 振动压实填石路堤动力响应试验研究[J]. 振动与冲击, 2014, 33(20): 151-156.

[12] CHEN Aijun, ZHANG Jiasheng, HE Jianqing, et al. Experimental study on dynamic response of vibratory compaction rockfill embankment [J]. Vibration and Shock, 2014, 33(20): 151-156.

The dynamic response of large diameter fill subgrade by large tonnage rollers

JIN Shubin1, ZHANG Changsheng2, LIU Zheng1, QIAO Shifan2

(1. Guizhou Highway Engineering Group Co., Ltd, Guiyang 550008, China；2. School of Civil Engineering, Central South University, Changsha 410075, China )

The dynamic stress of the soil in the third and fourth sections of Pan-xing highway was measured using the earth pressure cell during the rolling test. Based on the attenuation law of stress wave in the vertical direction, the energy attenuation function of dynamic stress was derived. A simplified model was established to analyze the compaction effect. A comparison was made with the measured values, which validated the accuracy of the model. The results were the number of rolling repetitions of no less than 8 times, optimum paving thickness of 100cm, the maximum particle size controlled to 50cm, roller maximum exciting force of 80t, and the construction parameters determined by the research results could effectively improve the quality of subgrade compaction.Key words: vibratory compaction; large particle size filler; rock fill subgrade; dynamic response

2015-12-28

贵州省交通厅科技资助项目(2015-122-047)

乔世范(1975-)，男，山东莒南人，教授，从事环境岩土工程及岩土信息三维可视化仿真技术等方面的教学和科研工作；E-mail:qiaoshifan@163.com

TU47

A

1672-7029(2016)09-1743-06