磁流变弹性体基于卡方分布的磁偶极子模型*
2016-10-19徐赵东许飞鸿
索 思,徐赵东,许飞鸿
(东南大学 混凝土及预应力混凝土结构教育部重点实验室,南京 210096)
磁流变弹性体基于卡方分布的磁偶极子模型*
索思,徐赵东,许飞鸿
(东南大学 混凝土及预应力混凝土结构教育部重点实验室,南京 210096)
为了精确描述磁流变弹性体的磁致效应,从而使磁流变弹性体应用于工程实际,基于磁偶极子理论,结合铁磁颗粒在磁流变弹性体中的分布特点,引入分布参量n,假设相邻铁磁颗粒的间距满足卡方分布,提出基于卡方分布的磁偶极子模型,推导了磁致剪切模量的表达式。该模型弥补了“均匀分布”假设的不足且形式简单,适于工程应用,同时可以精确反映出各因素对磁流变弹性体磁致效应的影响规律,其中分布参量和外加磁场强度是影响磁致效应的关键因素。
磁流变弹性体;磁偶极子模型;卡方分布;磁致剪切模量
0 引 言
磁流变弹性体是近10年来新出现的1种新型智能材料,其流变性能可随外磁场的改变而快速连续的变化。由于磁流变弹性体能够克服磁流变液易沉降、稳定性差的问题,因而它具有广阔的应用前景[1-2],并得到国内外学者的热切关注。目前,大部分研究集中于磁流变弹性体的制备与工程应用,其中美国Lord公司的Jolly等最先研究了磁流变弹性体的力学性能,并开发出了1种基于磁流变弹性的套筒[3-4];中国科学技术大学的龚兴龙教授团队研究了的各向同性和各向异性磁流变弹性体制备和力学性能,并设计了基于磁流变弹性体的智能吸振元件[5-7]等。然而,有关建立描述磁流变弹性体磁致效应力学模型的工作相对落后,主要有Jolly等[3]基于磁偶极子理论,考虑两个磁性颗粒间的相互作用,提出的磁偶极子模型;Shen等[8]基于耦合场理论,将磁流变弹性体中磁性颗粒简化为无限长链结构并考虑一条链中所有颗粒的相互作用,提出的耦合场模型;党辉等[9]基于麦克斯韦-玻尔兹曼分布,提出的分布链修正模型。然而上述的磁偶极子模型和耦合场模型均假设磁性颗粒在磁流变弹性体中均匀分布,与实际情况有一定的差距,磁致效应计算结果通常偏大;而基于麦克斯韦-玻尔兹曼分布的分布链修正模型表达式略为复杂,参数较多不易确定,难以用于工程中。
为了弥补以上模型的不足,本文基于磁偶极子模型,确定颗粒间距为影响磁流变弹性体磁致效应的关键因素,并分析了磁流变弹性体中磁性颗粒的分布,假定颗粒间距服从χ2分布,推导了磁流变弹性体的磁致剪切模量的计算公式,并分析了各影响因素对磁致效应的影响,为磁流变弹性体的工程应用打下基础。
1 模型假设
磁流变弹性体在硫化成型的过程中,受制作工艺、磁场强度和基材料性质的影响,铁磁颗粒的分布会有一定的差异,电镜照片[10]如图1所示。
由图1可以看出,在外加磁场作用下,铁磁颗粒在基体中都会形成链状结构,当外加磁场较小时,链结构较为松散;当外加磁场逐渐增大时,链结构逐渐加粗,颗粒趋于紧密。
将磁性颗粒简化为两个磁偶极子,如图2所示,其相互作用力[11]可表示为
式中,μ0为真空磁导率,r为磁偶极子间距,m1和m2为颗粒的磁偶极矩,r0为沿磁矩方向的矢量。
通过分析上式,可知磁偶极矩间相互作用力F近似与磁性颗粒间距r的二次方成反比,则当间距r增大时,相互作用力F将迅速减小,可见,链结构中颗粒的相互作用力主要取决于相邻颗粒的间距。
基于以上讨论,本文的计算模型主要有以下假设:(1)磁流变弹性体中铁磁颗粒尺寸相同,且磁化后其磁矩也是相等的;(2)铁磁颗粒的相互作用只存在于相邻颗粒之间,忽略其它颗粒的作用;(3)铁磁颗粒分布对磁流变弹性体磁致效应的影响主要表现在硫化成型后颗粒平均间距。由于硫化过程中外加磁场的作用,磁性颗粒在弹性体中的分布不会是均匀分布,而是呈现成链趋势,则相邻磁性颗粒的间距呈偏峰分布,假设该间距是符合χ2分布。该假设考虑了铁磁颗粒分布差异对磁流变弹性体磁致效应的影响,使模型弥补了均匀分布假设的不足,同时也不致使模型表达过分复杂,适宜用在工程实际中。

图1 不同外加磁场下铁磁颗粒分布
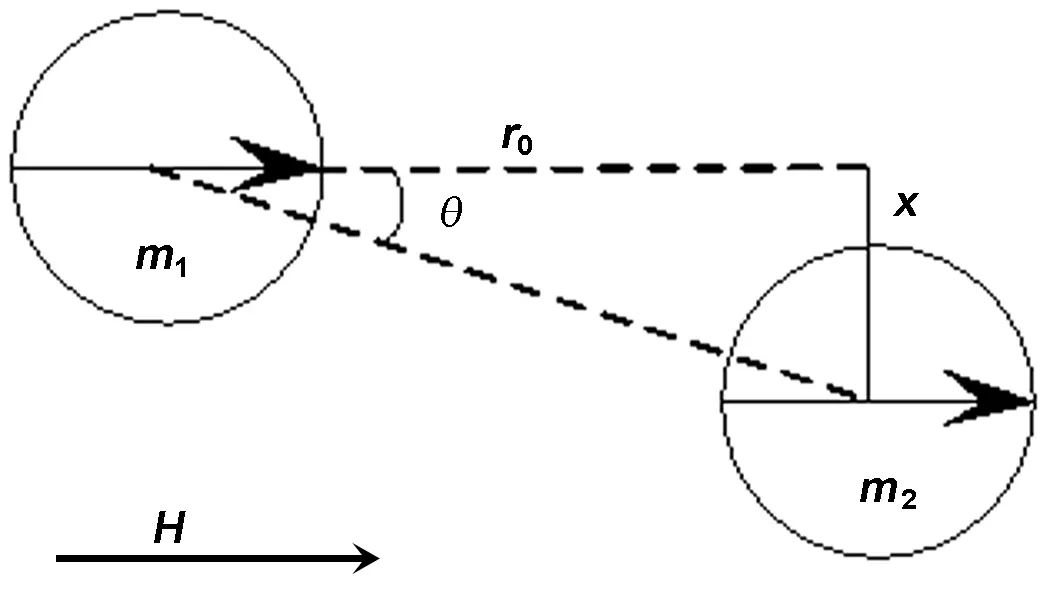
图2磁偶极子模型
Fig 2 Schematic of dipolar model
2 磁致剪切模量计算
采用磁偶极子模型进行分析,计算模型如图2所示。将外加磁场下的每一个颗粒简化为一个磁偶极子,在外加磁场H下,磁偶极矩分别为m1和m2的两个磁偶极子的相互作用能可表示为
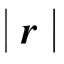
如图2所示,定义一条链的剪切应变为
则两偶极子的相互作用能写成
式中,磁偶极矩
式中,Jp为颗粒的极化强度。
为了表征相邻铁磁颗粒间的相对距离,引入随机变量h(h≥0),令
h越小,颗粒间距越小,两相邻颗粒构成的偶极子对相互作用能E12越大,当h=0时,表明相邻颗粒紧密相连,完全接触。将h代入式(4)可得
假设
式中,n表示随机变量h的期望值。分布参量n的大小可以反映相邻铁磁颗粒间距的平均水平,n越小,则磁流变弹性体中铁磁颗粒分布越密集,所以n可以作为一个反映MRE制备工艺以及基材料性质的综合指标。由于E12为h的函数,对E12求期望值
式中
表示铁磁颗粒分布的密集程度对磁流变弹性体磁致效应的影响。
设弹性体的总体积为Ve,每个颗粒的体积为Vi,那么颗粒的总数np可以表示为
式中,φ为颗粒的体积比,d为颗粒直径。
由于颗粒之间的相互作用能只存在于邻近颗粒之间,所以总体的磁场能等于E(E12)乘以总的颗粒个数np,进而弹性体中的平均能量密度可表示为
为求磁场能引起的磁致剪切应力,只需将式(9)对剪切应变γ求一阶导数
然后,磁致剪切模量可表达为
3 影响因素分析
铁磁颗粒磁化过程是非线性的,在理论分析中,外部磁场强度H与材料内部磁化强度Mp的非线性关系可根据Frolich-Kennely定理确定[12]
式中,Ms为磁饱和时的磁化强度,对于铁磁材料通常取μ0Ms=2.1 T;μp为铁粉的磁导率,低磁场中μp取1 000。
3.1分布参量n对磁致剪切模量的影响
由以上模型计算得出磁致剪切模量与分布参量n的关系如图3所示,其中参数取如下值:μ0=4π×10-7H/m,μ1=1,φ=0.3,γ=0.025,H0=400kA/m。
由图3可知,磁致剪切模量随着分布参量n的增大而减小,在n∈[0,2]时,磁致剪切模量下降很快,n≥2时,下降趋于缓慢,而当n≈6时,磁致剪切模量已接近于0,可认为磁致效应可以忽略不计。根据式(6)可知,参数n反映了磁流变弹性体中磁性颗粒间的平均距离,表征了磁性颗粒在磁流变弹性体中分布的密集程度,n越小磁性颗粒间的平均距离越小,磁性颗粒分布越密集,成链效果越好;而成链效果直接影响磁流变弹性体磁致效应的大小,所以降低n可以显著地改善磁流变弹性体的磁流变效应。
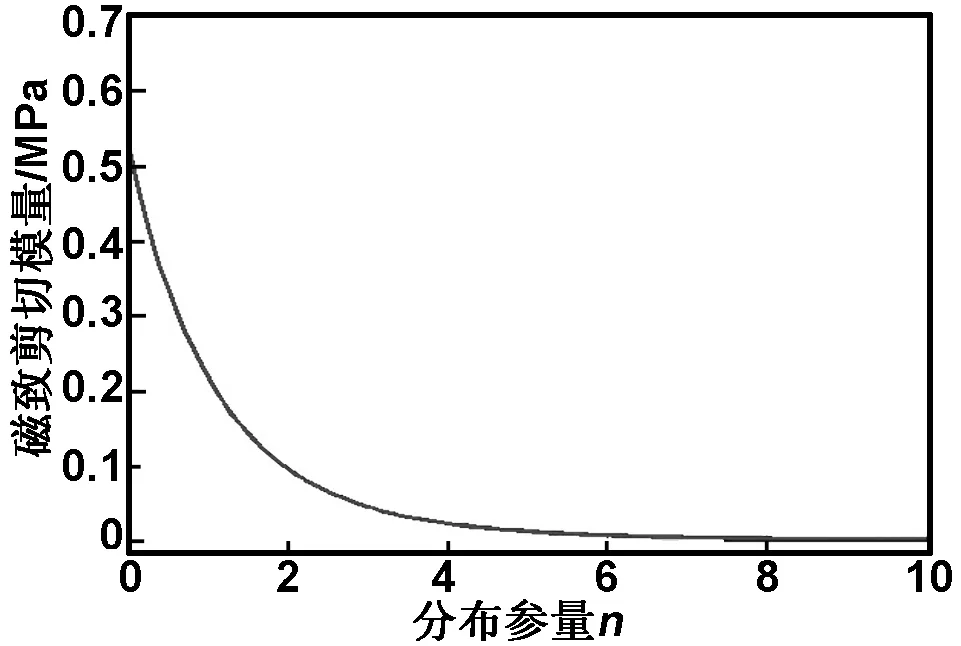
图3分布参量n与磁致剪切模量关系
Fig 3 Relationship between parameter n and magnetic-induced shear modulus
为进一步验证参数n对磁流变弹性体磁流变效应的影响,采用标准3参数固体模型对文献[13]中拟静态试验中BIIR-H-60和BIIR-H-70(60和70表示试样中铁磁颗粒的质量比为60%和70%)结果进行分析处理,试验结果如图4所示,根据以上模型,应力与应变关系可表示为
式中,A、B和C为待定参数。试验结果与数值模型误差可表示为
式中,m为实验数据数量,τM和τE分别模型计算结果和试验结果。
采用最小二乘法进行参数识别,结果如下:A=-0.0101 MPa,B=39 610,C=0.585 MPa;对于试样BIIR-H-60和BIIR-H-70,参数n分别为1.8422和1.5526。从试验结果(图4)可以看出,铁磁颗粒质量比越大,MRE试样的磁流变效应越显著,这主要是由于铁磁颗粒的分布会随颗粒含量的增加而趋于密集。同时,从参数识别结果也可以看出,参数n与铁磁颗粒质量比成负相关关系,这表明参数n可以有效地表征磁性颗粒在磁流变弹性体中分布的密集程度。

图4 拟静态试验结果
3.2切应变对磁致剪切模量的影响
由以上模型计算得出磁致剪切模量与切应变γ的关系如图5所示,其中参数取如下值:μ0=4π×10-7H/m,μ1=1,φ=0.3,n=2,H0=400 kA/m。
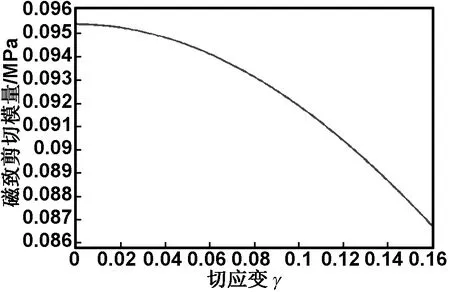
图5 切应变γ与磁致剪切模量关系
Fig 5 Relationship between shear strainγand magnetic-induced shear modulus
由图5可知,磁致剪切模量随切应变的增大而减小,这主要是由于切应变的增加使磁性颗粒间距增大,颗粒间由于磁场引起的相互作用力减小导致的。但从图5也可以看出,当应变较小时,这种由应变引起的刚度减小效应是很小的,通常可以忽略不计。
3.3外加磁场强度对磁致剪切模量的影响
由以上模型计算得出磁致剪切模量与外加磁场强度H的关系如图6所示,其中参数取如下值:μ0=4π×10-7H/m,μ1=1,φ=0.3,n=2,γ=0.025。

图6 磁场强度H与磁致剪切模量关系
Fig 6 Relationship between magnetic field intensity H and magnetic-induced shear modulus
由图6可知,当磁场强度H<200 kA/m时,磁致剪切模量随磁场强度的增加而增加,这是磁性颗粒的磁化强度逐渐增大使颗粒间的相互作用力逐渐增大的结果;而当H≥200 kA/m时,磁致剪切模量随磁场强度的增加不再增加,这主要是由于磁性颗粒达到磁饱和,磁化强度不再增大。
4 结 论
通过研究铁磁颗粒分布对磁流变弹性体磁致效应的影响,提出了基于卡方分布的磁偶极子模型,并得出以下结论:
(1)本模型弥补了“均匀分布假设”的不足,通过引入分布参量n来表征相邻铁磁颗粒平均间距,更好的反映了铁磁颗粒在磁流变弹性体中的分布差异对磁致效应的影响,同时该模型推导出的磁致剪切模量计算公式也综合反映了各因素对磁致效应的影响规律。
(2)磁致剪切模量会随分布参量n的增加而减小,n较小时,磁致剪切模量下降很快,当n≥2时,下降趋于缓慢,而当n≈6时,磁致剪切模量已接近于0,可认为磁致效应可以忽略不计。
(3)切应变的增大会引起磁致剪切模量的减小,但当切应变较小时,这种效应很小,通常可忽略不计。
(4)磁致效应会随外加磁场强度变化而变化,但当磁性颗粒达到磁饱和时,磁致剪切模量不会随外磁场强度的增加而提高。
致谢:感谢江苏省青蓝工程对项目的大力资助,感谢科技部中青年科技创新领军人才对本项目的大力资助!
[1]Wang Jianxiao,Meng Guang.Research advances in magnetorheologicalelastomers[J].Journal of Functional Materials,2006,37(5):706-709.
汪建晓,孟光.磁流变弹性体研究进展[J].功能材料,2006,37(5):706-709.
[2]Ginder J M,Nichols M E,Elie L D,et al.Magnetorheological elastomers:properties and applications[J].Proceedings of SPIE,1999,3675:131-138.
[3]Jolly M R,Carlson J D,Munoz B C.A model of the behaviour of magnetorheologicalmaterials[J].Smart Materials and Structures,1996,5(5):607-614.
[4]Jolly M R,Carlson J D.The magnetoviscoelastic response of elastomer composites consisting of ferrousparticles embedded in a polymer matrix[J].Journal of Intelligent Material Systems and Structures,1996,7(6):613-622.
[5]Gong Xinglong,Deng Huaxia,Li Jianfeng,et al.Magnetorheological elastomers and correspondingsemi active vibration absorption technology[J].Journal of University of Scinece and Technology of China,2007,37(10):1192-1203.
龚兴龙,邓华夏,李剑锋,等.磁流变弹性体及其半主动吸振技术[J].中国科学技术大学学报,2007,37(10):1192-1203.
[6]Chen Lin,Gong Xinglong,Kong Qinghe.Preparation and characterization of magnetorheological elastomers based on natural rubber[J].Journalof Experimental Mechanics,2007,22(3-4):372-378.
陈琳,龚兴龙,孔庆合.天然橡胶基磁流变弹性体的研制与表征[J].实验力学,2007,22(3-4):372-378.
[7]Chen Lin.The development and mechanical characterization of magnetorheological elastomers[D].Hefei:University of Science and Technology of China,2009.
陈琳.磁流变弹性体的研制及其力学行为的表征[D].合肥:中国科学技术大学,2009.
[8]Shen Y,Golnaraghi M F,Heppler G R.Experimental research and modeling of magnetorheological elastomers[J].Journal of Intelligent Material Systems and Structures,2004,15(1):27-35.
[9]Dang Hui,Zhu Yingshun,Gong Xinglong,et al.RevisedModel of the magnetorhelogical elastomer based on distributed chains[J].Chinese Journal of Chemical Physics,2005,18(6):971-975.
党辉,朱应顺,龚兴龙,等.基于分布链修正的磁流变弹性体的物理模型[J].化学物理学报,2005,18(6):971-975.
[10]Chen L,Gong X L,Li W H. Microstructures and viscoelastic properties of anisotropic magnetorheological elastomers[J].Smart Materials and Structures,2007,16(6):2645-2650.
[11]冯慈璋.极化与磁化[M].北京:高等教育出版社,1986.
[12]Ginder J M,Davis L C.Shear Stresses in magnetorheological fluids:role of magnetic saturation [J].Applied Physics Letters,1994,65(26):3410-3412.
[13]Zhu Juntao.Research on vibration isolation and attenuation of the broadband excitation platform by using magnetorheological elastomers[D].Nanjing:Southeast University,2013.
朱俊涛.磁流变弹性体对宽频激励平台隔减振研究[D].南京:东南大学,2013.
A model ofmagnetorheological elastomer based on chi-square distribution
SUO Si,XU Zhaodong,XU Feihong
(Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education,Southeast University,Nanjing 210096,China)
In order to describe the magnetorheological effect of magnetorheological elastomers accurately,and provide theory basis for the engineering application of MRE,a modified mathematical model is proposed based on the dipolar model.Analyzing the characteristic of ferromagnetic particles’ distribution in the elastomer,this model introduces n as a distribution parameter and assumes that the distance between two adjacent particles meets chi-square distribution,and the expression of magnetic-induced shear modulus is derived.This model overcomes the deficiency of the assumption that particles distribute uniformly in MRE,and it is simple in formation and apt for engineering application.Moreover,the expression of magnetic-induced shear modulus can reflect the law between the magnetorheological effect and each influence factor exactly,and results show the distribution parameter and magnetic intensity are the key factors.
magnetorheological elastomer; dipolar model; chi-square distribution; magnetic-induced shear modulus
1001-9731(2016)09-09063-05
江苏省自然科学基金资助项目(BK20140025)
2015-03-20
2015-06-15 通讯作者:徐赵东,E-mail:xuzhdgyq@seu.edu.cn
索思(1990-),男,山西大同人,在读硕士,师承徐赵东教授,从事智能材料研究。
TU599
ADOI:10.3969/j.issn.1001-9731.2016.09.012
