光学镜片亚表面损伤形成数值模拟与分析

任志英　高诚辉　陈为平　林有希

福州大学，福州，350108



光学镜片亚表面损伤形成数值模拟与分析

任志英高诚辉陈为平林有希

福州大学，福州，350108

针对当前光学镜片亚表面损伤的研究重点主要集中在加工工艺参数及磨粒粒径、分布等方面的现状，基于脆性材料压痕断裂理论，深入分析了加工过程所导致光学镜片亚表面损伤，对不同锐度角的磨粒在相同载荷不同加工速度下与光学镜片表面间的抛光过程进行了微观动态仿真。获得了在不同加工参数作用下磨头与镜片表面间的摩擦接触、应力应变分布及亚表面损伤等情况，归纳出亚表面损伤裂纹深度、亚表面损伤空穴深度、体积去除率、表面破损率、磨粒锐度角及磨抛速度等相关参数之间的关系，并得出如下结论：当磨粒锐度角为54°～58°,加工速度为7～8 m/s时，加工后的镜片在保证一定加工效率的同时，产生的亚表面损伤及表面破损率最小。

光学镜片；金刚石磨粒；亚表面损伤；磨粒锐度角；有限元仿真

0　引言

光学硬脆性材料在加工过程中不可避免引入的亚表面损伤将直接降低光学镜片的使用寿命，影响其工作的稳定性、光学成像质量及其抗激光损伤阈值等一系列重要的性能指标[1]。随着我国光学领域科技的不断发展，迫切需要制造出表面质量性能优异且无亚表面损伤的光学镜片，以保障重大光学工程的顺利实施。因此，如何快速、准确地检测和评价加工过程引入的亚表面损伤，如何有效去除亚表面损伤，已成为制约现阶段重大光学系统发展的瓶颈。优化加工工艺参数又是去除亚表面损伤，获得光滑、超光滑表面及提高加工效率和加工质量的依据。

为了得到最优的加工工艺技术，国内外学者在改善研磨及抛光过程的加工工艺参数以减少或消除亚表面损伤等方面进行了大量实验及理论研究和仿真工作。在实验及理论研究方面，文献[2-3]在分析、总结前人研究成果的基础上，进一步丰富和拓展了压痕断裂力学理论，为亚表面损伤的理论研究奠定了坚实的基础。Suratwala等[4]利用锥形表面抛光技术，从实验角度分析了熔融石英玻璃表面/亚表面损伤的分布特征及其随深度变化的规律，并建立了亚表面损伤的简易模型。Li等[5]通过实验分析了加工参数对亚表面损伤的影响，建立了亚表面损伤深度和元件表面粗糙度之间的理论模型，同时利用加工参数对亚表面损伤深度进行了预测。在仿真研究方面，李志强[6]基于GSS软件，分析了磨料粒度、研磨压力、磨具等对划痕深度、元件表面粗糙度等的影响，但是还没有形成一个完整的应用体系。刘超[7]用有限元分析软件ANSYS来建模，采用理想的平面和von Mises屈服准则来对不同类型磨粒对元件亚表面损伤的影响进行仿真。高平[8]利用有限元分析软件ABAQUS建立了模型，把磨粒角度简化为圆形，粗糙表面简化为理想平面来进行亚表面损伤的静态响应分析。文献[9-11]利用ANSYS有限元分析软件建立了单颗磨粒与光学镜片间的弹塑性本构关系模型，把磨粒统一简化成圆锥角为106°的理想圆锥体，光学镜片视为理想光滑平面，采用JH-2材料破坏模型来对亚表面裂纹的形成与扩展进行仿真，探究了砂轮线速度、磨粒粒径等对亚表面损伤的影响。

综上所述，关于光学镜片亚表面损伤的仿真建模分析，多数模型过于简化，如将磨粒视为球体而忽视实际存在的不规则锐度角；或是仅研究同一个锐度角对亚表面损伤的影响；或是将元件实际粗糙面视为理想平面等，这在一定程度上导致仿真结果与实际情况间产生了误差。因此，本文充分考虑到脆性光学材料在研抛中所引入的亚表面损伤，以及加工过程中压力、加工速度及磨粒等相关参数的影响，从微观动力学角度动态模拟不同锐度角磨头与粗糙光学镜片之间的抛光过程，根据脆性材料的压痕断裂理论，分析在剪切强度一定的情况下，不同研抛速度和磨粒锐度角对光学镜片亚表面损伤的影响，从而得出最优磨粒形态特征，以指导实际加工过程，最终取得最佳的加工效果。

1　亚表面损伤力学模型的建立

1.1力学模型的建立与分析

为了对动态仿真过程有定量的理解，建立单颗磨粒与光学镜片进行磨抛时的滑动接触力学模型，考虑到磨粒的表面真实性，采用了具有分形特征的粗糙表面，同时由于磨粒粗糙表面的微凸体具有圆锥体的一般形式，故假设磨粒分形表面圆形微凸体为圆锥体，则分形磨粒表面微凸体与粗糙表面接触过程中的受力分析如图1所示[12]。

图1　磨粒与光学镜片间滑动摩擦接触过程受力分析

图1中，圆锥形磨粒的锐度角(半角)为θ；工件的屈服应力为σy，是与工件的屈服强度有关的常数。当磨粒在法向力N和切向力Ft的作用下接触到工件表面时，磨粒开始滚动并印压工件表面。在磨粒与工件接触区域内用于平衡磨粒受力的外部载荷有法向力Fn和摩擦力(FL和Fm)，假设所受载荷Fn、FL、Fm的合力沿着磨粒的锥形边。其中，磨粒的法向力是由研磨液的流体动压等导致的，而切向力是在滚压过程中快速运动产生的。则可推导得出：

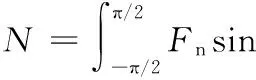
(1)

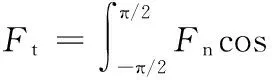
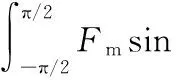
(2)

其中，外部载荷Fn、FL、Fm可分别表示为

(3)

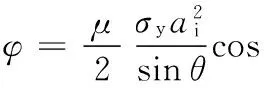
(4)

(5)

式中，μ为磨粒与元件间的摩擦因数；σy为元件的屈服应力，MPa；ai为塑性变形区的半径，mm；A为磨粒与基体间的接触面积。

将式(3)、式(4)代入式(1)，整理得

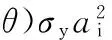
(6)

将式(3)～式(5)代入式(2)，整理得

(7)

则式(6)和式(7)分别为施加到单颗磨粒上的法向作用力和切向作用力公式。

1.2有限元数值模型的建立

在建立研抛数学模型时，为了保证网格的顺利划分，提高计算效率及计算精度，在几何建模中提出以下假设和简化：

(1)忽略磨粒分布与磨粒尺寸的不均匀性问题对研抛过程中压力的影响，认为磨粒粒径相同且均匀分布。

(2)假设光学镜片的自转速度与主轴转速相同。

(3)因磨粒硬度远大于光学镜片硬度，可认为建模时的磨粒为刚性体，在运动过程中不会引起磨粒形状的改变。

(4)假设光学镜片固定不动，磨粒随抛光盘一起相对光学镜片进行运动。

在模型参数方面，选用常见的120号金刚石磨粒和K9玻璃作为实验材料[5,13]。磨粒属性见表1。根据文献[14]，为更加贴近实际情况，本文考虑磨粒锐度角对亚表面损伤可能产生的影响，并通过分析文献[15]确定了一个合适的锐度角范围，如图2所示。粗糙表面在不同观察尺度下具有良好的自相似性[16-17]，而这种自相似性可以用分形几何来表征。故本文采用W-M函数[18]分形表面(D=2.5)模拟光学镜片表面特征，建立了长为4056 μm、宽约330 μm、高约300 μm的三维粗糙表面模型。

表1　磨粒属性

图2磨粒锐度角分布

在参数设置方面，进行破坏机制设置时，选择了更适合脆性材料断裂的Brittle Cracking，而不是通常的塑性破坏及等效应力极限等；在载荷设置时，对磨粒施加一定的集中载荷，并设置其幅值曲线，使之能够线性施压，避免材料因瞬时应力集中过大而出现不符合实际情况的破坏。最后，为了更加直观地观测、分析金刚石磨粒与分形粗糙表面微凸体相互接触过程的动态变化，建立了两者间的二维数学模型，并采用更具非线性分析能力的有限元软件ABAQUS进行光学镜片亚表面损伤的动态仿真。该模型的网格划分如图3所示，仿真参数见表2。

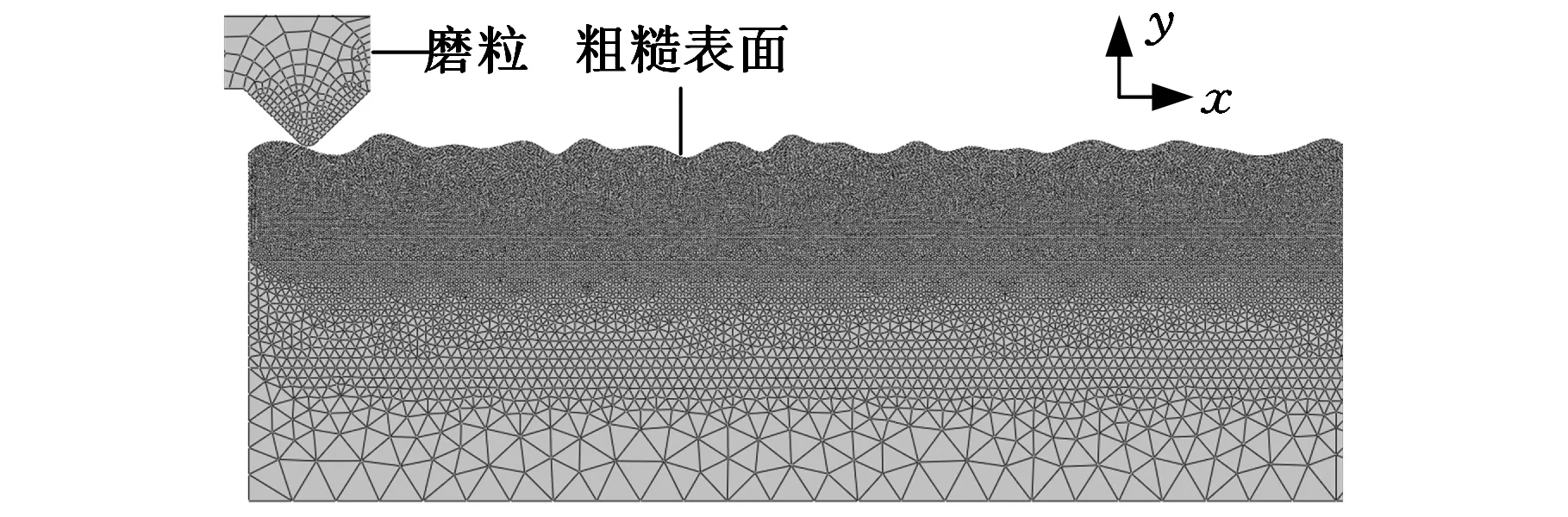
图3　磨粒与粗糙表面的网格划分

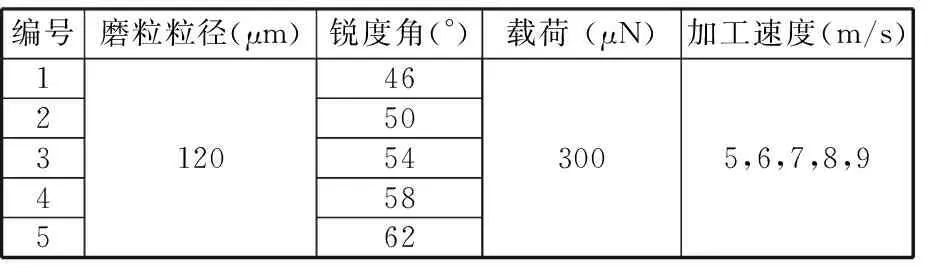
编号磨粒粒径(μm)锐度角(°)载荷(μN)加工速度(m/s)1234512046505458623005,6,7,8,9

2　动态仿真结果与相关参数分析

2.1模型仿真结果及应力分析

光学镜片亚表面损伤的形成过程是应力不断发生变化的动态过程，本文以磨粒与粗糙光学镜片表面微凸体摩擦过程中的接触时间点作为参考点，来反映整个动态过程的变化情况。图4～图15所示为该动态仿真中微观裂纹的成核及扩展过程，其中磨粒与光学镜片表面间接触过程被认为是一个从不断加载到逐渐卸载的动态过程。

图4　磨粒与光学镜片表面未接触(t=0.680 02 ms)

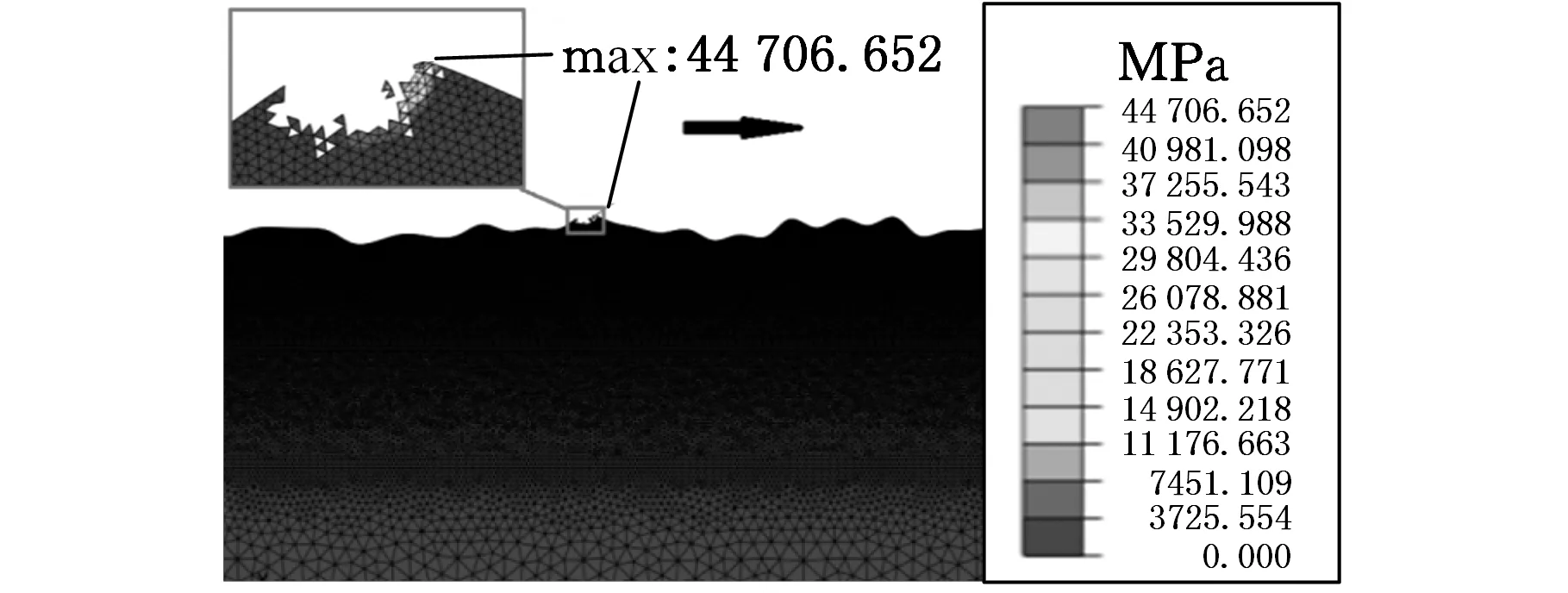
图5　磨粒与光学镜片表面刚刚接触(t=0.685 08 ms)

图6　磨粒与光学镜片表面接触中(t=0.690 02 ms)

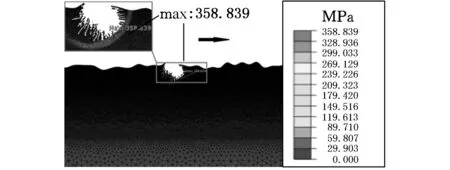
图7　磨粒与光学镜片表面接触后(t=0.695 08 ms)

图8　磨粒与光学镜片表面接触后(t=0.700 02 ms)

图9　磨粒与光学镜片表面接触后(t=0.705 08 ms)

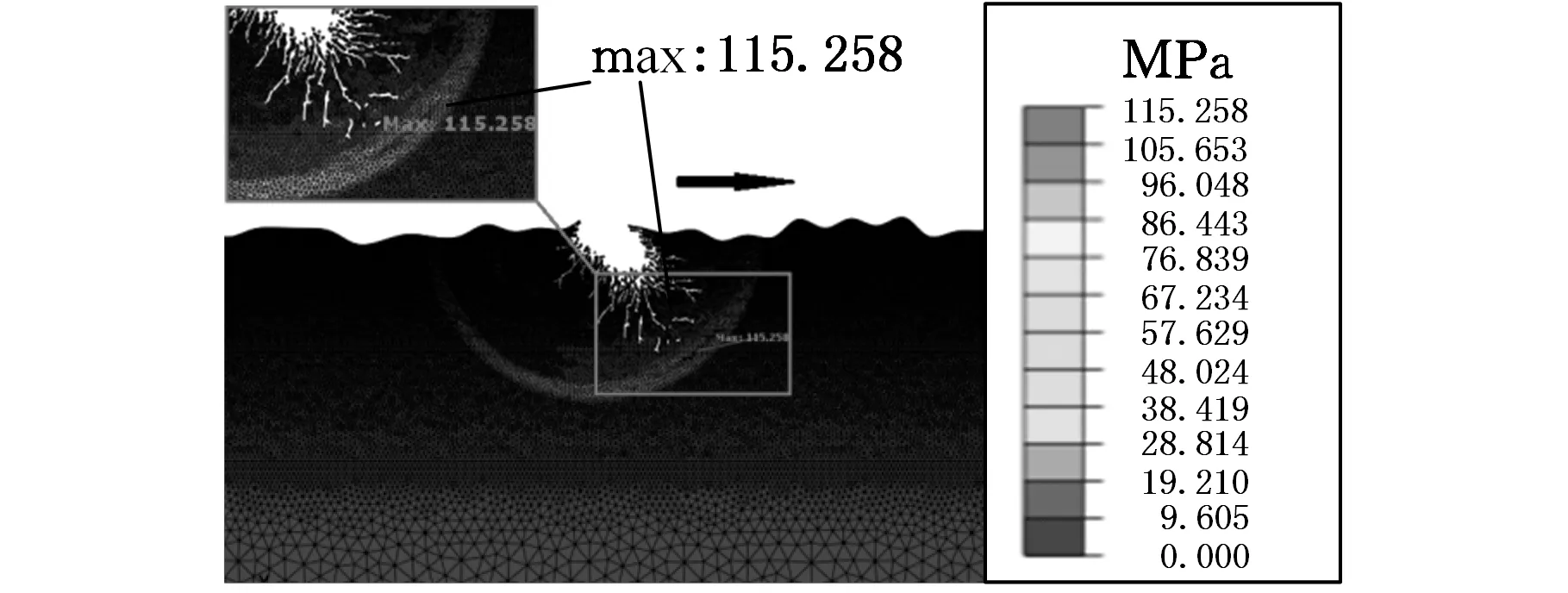
图10　磨粒与光学镜片表面接触后(t=0.710 02 ms)

图11　磨粒与光学镜片表面接触后(t=0.715 08 ms)

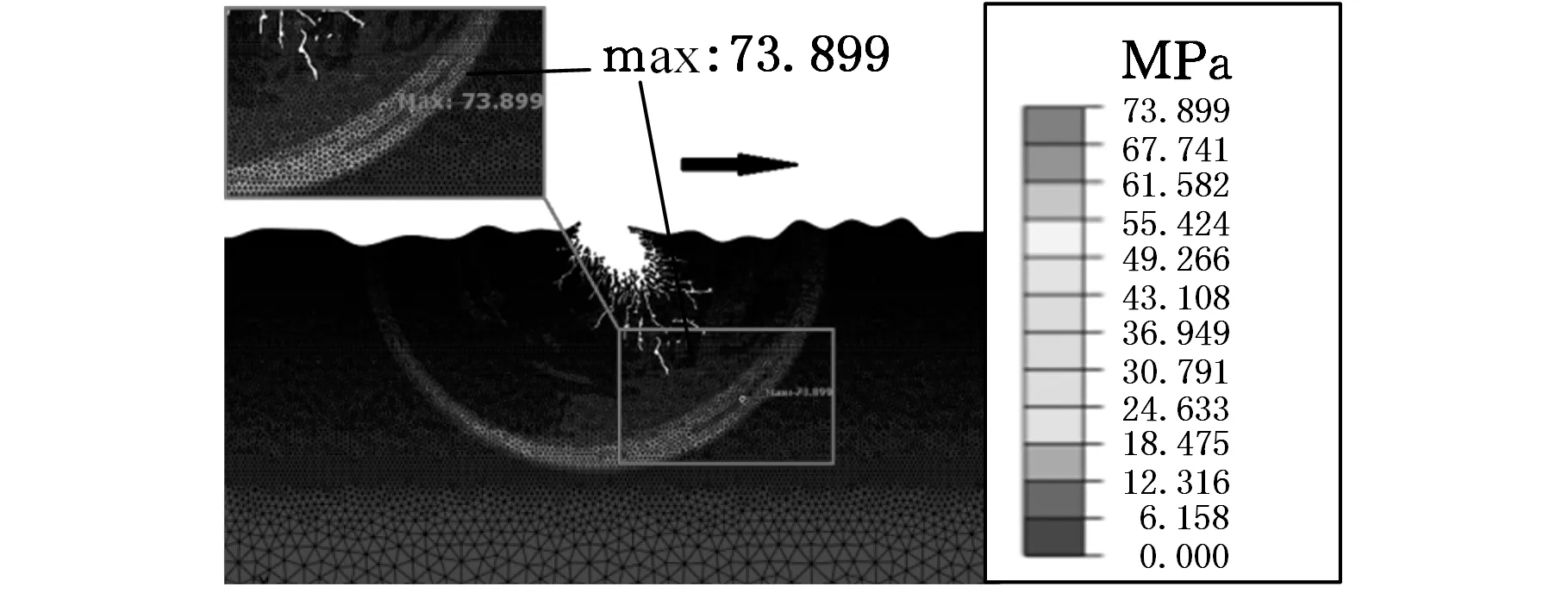
图12　磨粒与光学镜片表面接触后(t=0.720 02 ms)

图13　磨粒与光学镜片表面接触后(t=0.725 08 ms)

图14　磨粒与光学镜片表面接触后(t=0.730 02 ms)

图15　中位、侧位裂纹分布

从图4～图15可知，刚开始加载时，磨粒与试件表面处于未接触状态，此时磨粒受到一个向下的载荷，并开始向右运动，粗糙表面保持完好，没有任何破坏，见图4；随着载荷的继续增大，磨粒与粗糙表面开始接触，如图5所示，可清楚地看出，在刚接触时，由于瞬时应力很大，粗糙面严重变形，造成与之接触的局部材料直接从基体上被去除，此时最大应力值达到44 706.652 MPa；接触继续进行，由于受到磨粒的挤压作用，试件表面的去除量进一步增加，形成了小型的“凹坑”，如图6所示，此时最大应力值为885.282 MPa；由于磨粒滑动速度较快，所以整个加载过程极为短暂。

当磨粒离开试件接触区，类似卸载过程。当磨粒划过接触区，试件不再受到挤压，故“凹坑”大小基本定型，环形的应力分布圈开始显现，伴随出现了细微的亚表面裂纹，裂纹没有特定的方向，沿着破坏处呈圆弧形分布，如图7所示；随着进一步的卸载，由于应力的大小超过了材料本身的屈服极限，故裂纹随着应力圈的扩散而向基体扩展，且大部分裂纹的扩展趋势与合力方向是一致的，如图8所示；随着运动的进行，裂纹开始向旁边扩展，形成了实际工况中常见的人字形、L形等裂纹；随着应力的逐渐变小，裂纹扩展速度也变慢，并最终变为零，如图14所示。图15所示为磨粒研磨过程中产生的中位裂纹及侧位裂纹的情况，可以看出侧位裂纹主要分布在近表面处，有向表面扩展的趋势；而中位裂纹的分布趋势与合力的方向是一致的。

上述亚表面损伤形成过程即裂纹的成核和扩展过程，也是磨粒和试件接触产生的应力随时间和亚表面深度的变化过程。由于亚表面损伤的形成是连续的动态过程，一般很难准确判断每个节点的应力变化，故选取该动态过程中具有最大应力的节点来分析该应力变化过程。考虑到图像视觉效果和美观，排除了图5中瞬时接触时出现最大应力的节点，故选取了从图6到图14过程中处于最大应力的9个节点。其变化曲线如图16、图17所示。

图16　应力-时间关系变化曲线图

图16所示为光学镜片亚表面损伤产生过程中应力随时间变化的曲线，从图16可知，应力随时间的变化呈现递减趋势，且前面衰减较快，而后

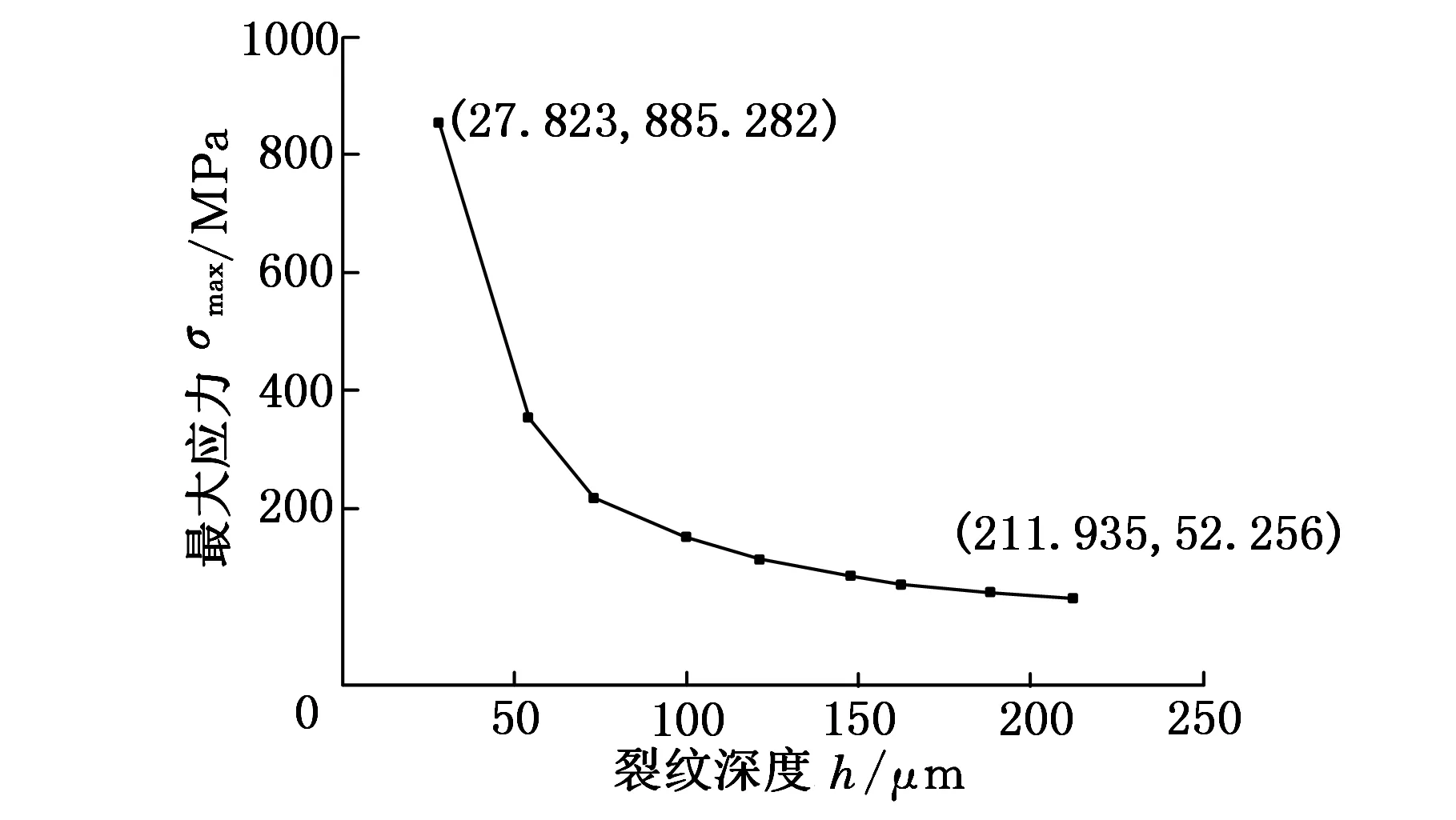
图17　最大应力与亚表面裂纹深度的关系

逐渐减缓，当时间超过0.72 ms时趋近于零，也就是应力随时间基本不再发生变化。图17所示为光学镜片亚表面损伤产生过程中最大应力随裂纹深度变化的曲线，对比图16发现，应力随深度呈递减趋势，且一开始递减较快，当裂纹深度距表面100 μm以上时速率逐渐变缓，直至不变。该现象与实际磨抛过程中亚表面损伤应力分布过程高度一致。

2.2研抛工艺参数对镜片亚表面损伤的影响

研究加工工艺参数对亚表面损伤影响的最终目的是能够加工出质量更高的光学镜片，以及提高加工效率，前者由亚表面损伤深度及光学镜片的表面破损率来判断，而加工效率的高低可由材料的去除率来反映。则该动态仿真过程中，在保持进给量不变的情况下，磨粒锐度角分别取46°、50°、54°、58°、62°，相对加工速度分别取5 m/s、6 m/s、7 m/s、8 m/s、9 m/s时，亚表面裂纹深度、亚表面空穴深度、体积去除率及表面破损率等相关加工参数之间的关系如图18～图21所示。

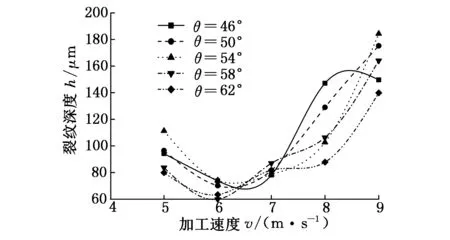
图18　磨粒锐度角与加工速度及亚表面裂纹深度关系

从图18中可以看出各曲线整体上呈现出一种先减小再递增的趋势。当加工速度为5 m/s时，54°锐度角要略大于其他角度产生的裂纹深度；当加工速度增大为6～7 m/s时，各锐度角产生的裂纹深度都比较接近且较小；当加工速度达到8 m/s时，出现了明显的分化，可以看出46°锐度角产生的裂纹深度要大于其他锐度角产生的裂纹深度，其次是50°锐度角产生的裂纹深度，62°锐度角产生的裂纹深度最小；当加工速度达到9 m/s时，裂纹深度较大，不适合加工。

从图19中可以看出一个整体变化趋势就是空穴的深度随加工速度的增大而呈现出递增的趋势。加工速度为5 m/s时，各锐度角产生的空穴深度基本一致；当加工速度增大到6 m/s时，可以看出62°锐度角产生的空穴深度是最小的，而54°锐度角产生的空穴深度是最大的；当加工速度达到7 m/s时，各个角度产生的空穴深度较小且比较接近；当加工速度增大到8 m/s时，50°锐度角产生的空穴深度要明显大于其他锐度角产生的空穴深度；当加工速度达到9 m/s时，可以看出46°锐度角产生的空穴深度要显著小于其他锐度角产生的空穴深度。

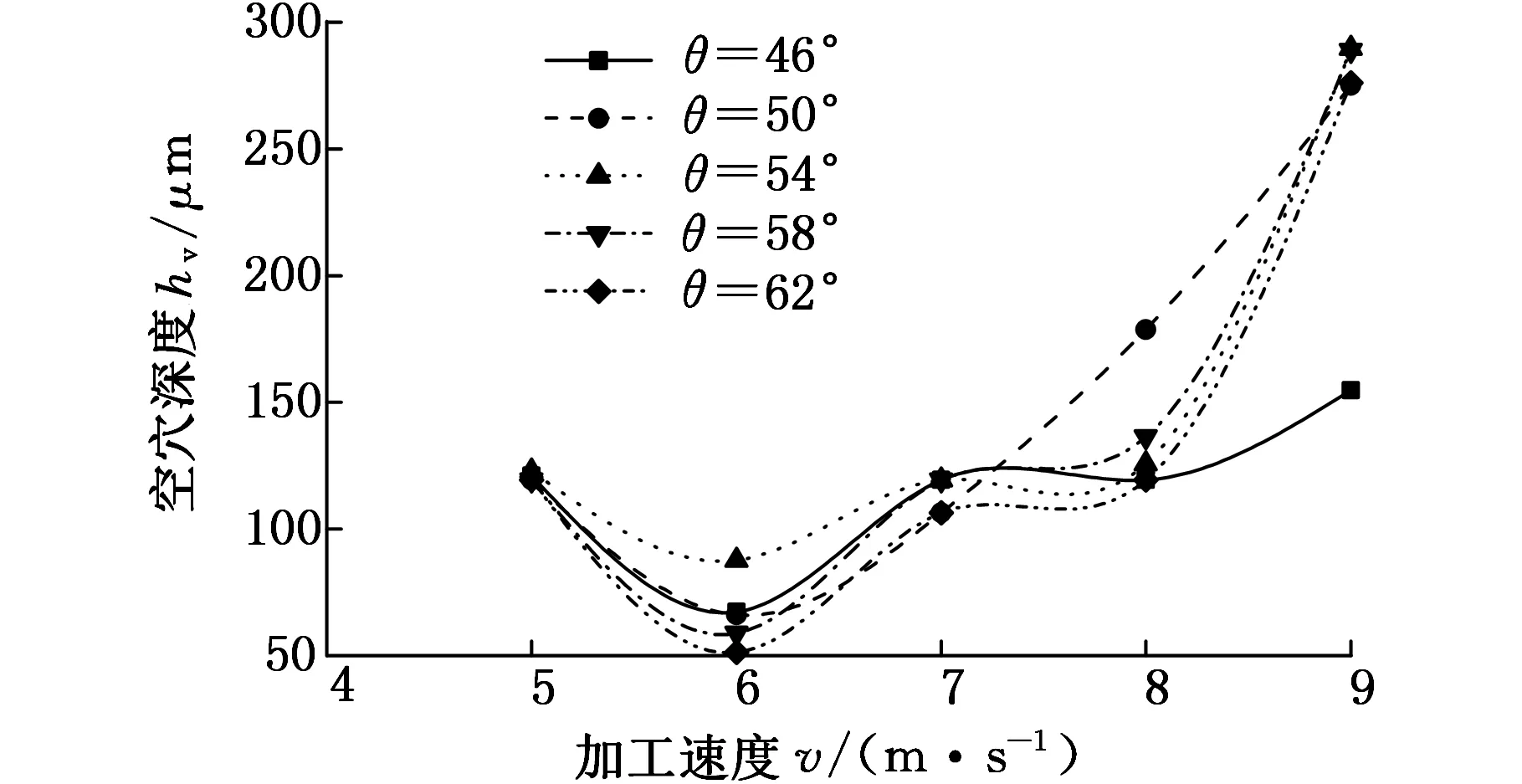
图19　磨粒锐度角与加工速度及亚表面空穴深度关系

从图20中可以看出各曲线呈现出一种先减小后递增的变化趋势；当加工速度为5 m/s时，各个锐度角产生的材料去除率基本一致，为4×106μm3/s左右；当加工速度达到6 m/s时，去除率开始减小；当加工速度为7 m/s时去除率又开始递增，明显大于加工速度为6 m/s时的去除率，各锐度角产生的去除率较为接近；当加工速度达到8 m/s时，各锐度角的去除率发生了明显的分化，其中46°和50°锐度角产生的去除率比其他角度产生的去除率要大；当加工速度达到9 m/s时，去除率进一步增大，其中54°锐度角产生的去除率要明显大于其他锐度角产生的去除率。

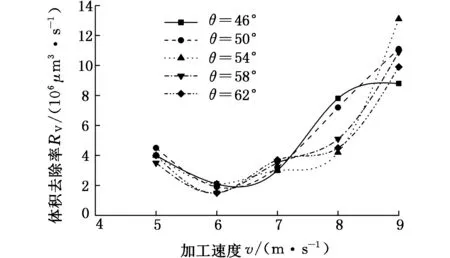
图20　磨粒锐度角与加工速度与体积去除率关系

从图21中可以看出各曲线呈现出一种先减小再增大的共同趋势；当加工速度为5 m/s时，54°锐度角产生的表面破损率要明显高于其他角度产生的破损率，当加工速度为6 m/s时，破损率达到最低水平且各锐度角较为接近；当加工速度达到7 m/s时，破损率略微增大，62°锐度角产生的表面破损情况比其他的表面破损情况更严重，58°锐度角产生的表面最优；当加工速度达到8 m/s时，破损率进一步增大，此时50°锐度角产生的表面破损情况最为严重；当加工速度达到9 m/s时，各锐度角产生的破损率发生明显分化，54°锐度角产生的表面破损率最大，其次是62°锐度角产生的表面破损率。

图21　磨粒锐度角与加工速度及表面破损率关系

3　结语

(1)由对亚表面损伤过程中各节点最大应力与时间、亚表面深度间的分析可知：应力随时间及亚表面深度的增大而逐渐减小，且应力减小的速率为先急后缓，亚表面裂纹深度超过100 μm后应力减小的速率明显变慢。

(2)由对磨粒锐度角、加工速度、亚表面裂纹深度及空穴深度的分析可知：从整体上看，加工加工速度为6～8 m/s时，产生的亚表面裂纹深度及空穴深度都较小，比较有利于加工；且该过程中46°和50°锐度角导致的裂纹和空穴深度较大，不适合进行加工。

(3)由对磨粒锐度角、加工速度、体积去除率及表面破损率的分析可知：从整体上看，加工速度为6 m/s时，产生的体积去除率最低，而5 m/s和9 m/s加工速度导致的表面破坏较严重，不适合进行加工；62°磨粒锐度角在保持相同去除率时导致的表面破损率较高，不利于加工。

(4)综上所述，在相同进给量情况下，最适合进行光学镜片磨抛加工的参数如下：磨粒锐度角为54°～58°，加工速度为7～8 m/s，此时加工出来的工件能在保持一定去除率的同时，产生最小的亚表面损伤和最低的表面破损率，使得加工质量得以保证。

[1]王卓.光学材料加工亚表面损伤检测及控制关键技术研究[D].长沙:国防科技大学，2008.

[2]Lambropoulos J C, Jacobs S D, Gillman B E,et al.Deterministic Micro-grinding, Lapping, and Polish-ing of Glass-ceramics[J]. Journal of the American Ceramic Society,2005, 88(5):1127-1132.

[3]Weyl W A.Structure of Subsurface Layers and Their Role in Glass Technology[J].Journal of Non-Crystalline Solids,1975,19:1-25.

[4]Suratwala T, Wong L, Miller P, et al.Sub-surface Mechanical Damage Distributions during Grinding of Fused Silica[J].Journal of Non-Crystalline Solids, 2006, 352(52):5601-5617.

[5]Li Shengyi，Wang Zhuo，Wu Yulie,et al.Prediction Theory and Experiment of Subsurface Damage Based on Lapping Processing Parameters[J].Journal of Mechanical Engineering,2009, 45(2):192-198.

[6]李志强.单元结构研磨盘的仿真与实验研究[D].杭州:浙江工业大学,2010.

[7]刘超.工程陶瓷磨削表面/亚表面损伤的模型建立和实验研究[D].天津：天津大学,2007.

[8]高平.光学玻璃研磨加工后亚表面损伤研究[D].南京:南京航空航天大学, 2012.

[9]孟彬彬.光学玻璃磨削裂纹形成过程仿真及试验研究[D].哈尔滨：哈尔滨工业大学,2011.

[10]Shen Linyan,Li Beizhi,Yang Jianguo.Simulation Study of Optical Glass Grinding Mechanism[J].Technology and Test,2010(2):104-106.

[11]Qi Weihua, Li Beizhi, Yang Jianguo, et al. Simulation Study of Glass Grinding Mechanism Based on Single Diamond Grit[J]. Tool Engineering, 2009 (9):17-20.

[12]Yang Fuqian, Kao I. Free Abrasive Machining in Slicing Brittle Materials with Wiresaw[J]. Journal of Electronic Packaging, 2001, 123(3):254-259.

[13]Wang Zhuo, Wu Yulie, Dai Yifan, et al. Rapid Detection of Subsurface Damage of Optical Materials in Lapping Process and Its Influence Regularity[J].Optics and Precision Engineering,2008,16(1):16-21.

[14]李改灵.光学材料磨削加工亚表面损伤测量的理论与实验研究[D].长沙:国防科技大学,2006.

[15]Wang Zhuo, Wu Yulie, Dai Yifan, et al. Research on Measurement and Prediction Methods of Subsurface Damage Depth of Optical Materials in Grinding Process[J]. Aviation Precision Manufacturing Technology,2007,43(5):1-5.

[16]Mahmoud T A, Tamaki J, Yan J W. Three-dimensional Shape Modeling of Diamond Abrasive Grains Measured by a Scanning Laser Microscope[J]. Key Engineering Materials, 2003, 238/239(6): 131-136.

[17]葛世荣,朱华.摩檫学的分形[M].北京:机械工业出版社,2005.

[18]Sahoo P, Ghosh N. Finite Element Contact Analysis of Fractal Surfaces[J].Journal of Physics D:Applied Physics,2007,40(14): 390-393.

(编辑陈勇)

Numerical Simulation and Analysis on Formation of Subsurface Damages of Optical Lenses

Ren ZhiyingGao ChenghuiChen WeipingLin Youxi

Fuzhou University,Fuzhou，350108

In view of the current research on the subsurface damages of the optical lenses, people mainly focused on the process parameters and abrasive particle size, distribution, and et al. Based on the theory of indentation fracture of brittle materials, this paper analysed a series of processes which led to subsurface damages of the optical lens, and then finished the micro dynamic simulation of the polishing process of optical lens surfaces under the different sharpness angles of the grains,and with the same load and the different processing speeds. Finley, this paper obtained the frictional contact, the stress and strain distribution and subsurface damages between abrasive and the lens’ surface. The relationship among the relevant parameters of the subsurface damage depth of crack, the subsurface damage depth, hole volume removal rate, surface damage rate, abrasive sharpness angle and grinding speed was summed up. When the grinding grain sharpness angle is as 54～58 degrees, the processing speed is as 7～8 m/s, then with the required processing efficiency subsurface damages and the damage rate of the machined lenses are of the minimum.

optical lens；diamond abrasive；subsurface damage；grit sharpness angle；finite element simulation

2015-07-01

国家自然科学基金资助项目(51175085，51205062，51375094);福建省自然科学基金资助项目(2015J01195)；清华大学摩擦学国家重点实验室开放基金资助项目(SKLTKF13B02);福州市科技局资助项目(2014-G-74)

TH161.14

10.3969/j.issn.1004-132X.2016.19.020

任志英，女，1980年生。福州大学机械工程及自动化学院讲师、博士。主要研究方向为工程表面特征提取、表面表征方法等。高诚辉，男，1953年生。福州大学机械工程及自动化学院教授、博士研究生导师。陈为平，男，1989年生。福州大学机械工程及自动化学院硕士研究生。林有希，男，1967年生。福州大学机械工程及自动化学院教授、博士研究生导师。