基于演化博弈理论的集群式承接产业转移模式选择研究*

李停

【区域格局与产业发展】

基于演化博弈理论的集群式承接产业转移模式选择研究*

李停

集群式产业转移是有限理性的企业在产业转移过程中的群体决策、调整及决策稳定的过程。论文基于演化博弈模型，对水平型和垂直型集群式产业转移的条件及稳定性进行研究。结果表明，只要企业单方面转移收益超过成本，集群式产业转移是市场机制的内生必然结果；政府干预，无论是增加转移收益还是减少转移成本，虽然不能确保集群式产业转移，但由于临界值水平的下降，增加了集群式产业转移的成功概率；在垂直型产业转移过程中，政府同等程度的政策优惠给核心企业对集群式产业转移成功实施的概率影响更大，证明“抓大放小”模式在现阶段比“筑巢引凤”模式更具有可行性。

演化博弈；集群式产业转移；演化博弈均衡；转移条件；稳定性

一、理论基础与文献综述

随着国际产业分工主导形式从产业间至产业内进一步向产品内的分工形式演变，产业集群式转移俨然已成为当前产业转移的主旋律。在产品内国际分工的背景下，单个企业一般只从事产品生产的一个或者几个环节，产品生产的关联性使产业转移已不再是孤立地、分散地进行，倾向于整体性的集群式转移形式。集群式产业转移又被称作产业链式转移、抱团式迁徙，表现为大量具有横向、纵向联系的关联企业以及相关科研机构空间上抱团从转出地向承接地整体迁徙。

共生理论为产业集群式转移的动因提供了一个十分有效的分析思路，产业集群式转移与生物种群共生迁徙有许多惊人的相似之处。面对生存环境的恶化，如食物减少、水资源下降等，这一栖息地生物群落原有的生物个体往往选择整体迁徙，类似于“蚂蚁搬家”那样，以便在新栖息地维持原有的共生系统。产业转移的实质是企业空间的扩张过程，也是企业的再区位或区位调整过程。同样的道理，集群产业面临经济环境的改变，典型的如要素价格上涨，集群内的企业可以通过集群式产业转移在承接地继续维持以往的分工和协作关系。

正是基于集群式产业转移与生物种群的整体迁徙机理的相似性，论文利用在生物进化研究中获得极大成功的演化博弈理论，分析不同情形下集群式产业转移的条件及稳定性。将集群式转移视作“有限理性”的企业在产业转移过程中的竞合行为，是群体成员策略互动、策略调整和策略稳定的动态演化过程，类似于生物共生进化。本质上讲，产业集群式转移就是有限理性的企业在产业转移过程中的竞争与合作行为，这种竞合行为与生物种群的竞争合作是相通的。面临转移后境况的不确定性，对成功企业的模仿和失败企业的惧惮，企业由直觉引导的行为方式与动物迁徙行为十分相似，因此借鉴生态行为学规律分析产业转移具有可行性。生态学家Lewontin最早利用演化博弈理论研究动植物的进化，发现动植物进化的结果多数情况下都可以用博弈论的纳什均衡来解释。行为学家Smith 和Price提出了演化博弈的核心概念“进化稳定策略”（evolutionarilystablestrategy，简记ESS）。随后，Taylor和Jonker进一步提出演化博弈理论的基本概念—模仿者动态（replicator dynamics），核心思想是具有较高收益的策略的复制速度快。随后演化博弈理论大量应用于社会学、经济学领域来研究群体行为的演化规律。Conlisk利用离散时间动态模型检验参与人的策略选择是否总是完全理性的，Weitizman利用演化博弈理论分析股份制经济等企业组织形式，Peyton Young将演化博弈理论用于分析社会风俗、传统习惯、行业规范等非正式合约的形成原因与演化路径。青木昌彦开创性地将演化博弈理论引入到制度分析，认为经济制度的产生具有路径依赖性，并随着内外部环境的变化逐渐演进。

从国内来看，近年来演化博弈模型在经济学、管理学和其他社会科学中也得到了广泛应用。李宗泰等运用演化博弈理论探讨食品质量安全监管问题，赵湜等构建了科技保险险种创新演化博弈模型，刘永亮等对煤炭安全管理与矿工违章行为进行演化博弈分析。演化博弈应用到集群式产业转移方面，任志安等认为企业集群实质上是一个网络外部化的过程，其形成过程类似于有限理性下的复制动态演化博弈，于斌斌基于演化博弈模型研究产业集群产业链和创新链的对接，王长峰使用演化博弈模型研究产业集群中的竞争与合作关系。刘友金等最先运用演化博弈模型探讨对称互惠共生和非对称互惠共生两种模式下集群式产业转移达到进化稳定的实现条件。刘友金的研究中未能将第三方力量政府加入后博弈收付的变化纳入博弈模型中，使得该研究只能停留在理论层面，无法深入探讨政府的各项政策对均衡调整、均衡稳定性的影响。

二、模型基本前提假设和博弈收付矩阵

刘友金等认为集群式产业转移有两种模式：产业链带动下的集群式产业转移和核心企业带动配套企业的集群式产业转移。联系到共生理论，前者是水平分工的企业借助集群式产业转移维持在转出地已经形成的对称互惠共生系统，企业之间地位和共生能量对等且没有从属关系，集群式产业转移利益主要源于产业层面的外部经济性；后者配套企业从属于核心企业，以垂直分工形式为主，在原共生系统中处于非对称互惠共生模式，产业转移利益主要是源于产业集群在资源配置上能综合市场和科层组织的优势。

本文将集群式产业转移分为水平型和垂直型两种形式，分别对应对称互惠共生和非对称互惠共生，讨论两种情形下产业集群式转移条件、稳定性差异，以及政策性因素对成功实施集群式产业转移的影响有何不同，从而揭示产业集群式转移的基本规律，为制定科学的引导产业转移政策提供理论依据。研究假设如下：（1）集群中企业具有有限理性特征，参与者不可避免地出现逻辑推理偏差和预期偏误导致决策失误，但参与者主观上有创造某种机制弥补自身理性不足的激励，对成功企业的模仿和对失败企业的惧惮引导其行为方式改变。企业独立做出转移或者不转移的决策，产业集群式转移是参与人反复决策、复制动态的博弈过程。（2）参照生物进化复制动态模型的一般设定，这里假定群内企业采用某种特定策略的相对变化率（变化速度与其比重）和其收益超过期望收益的幅度成正比。（3）假定水平型集群式产业转移涉及产业共有q个企业，企业产品差异化小，彼此间有很强的替代性。水平型产业集群式转移的动因是维持在转出地的对称互惠共生系统，因此参与企业的收益和成本具有对称性。设A、B是任意两个参与水平型集群式产业转移的企业，若同时转移可以产生Δπ的增量利润被两企业分享；企业单方面转移一方面给该企业带来r的收益（可能的原因是承接地低廉的要素价格或政策优惠），同时也会产生转移成本c（可能的原因是外部规模不经济或知识的溢出效应降低等）。r和c的大小关系不确定，在产业转移初期，r＜c的可能性较大。另外单个企业转移也给竞争对手带来-π的利润损失。图1给出了水平型集群式产业转移博弈的收付矩阵，数据都是与转出地市场相比的净变动值。（4）垂直型集群式产业转移涉及核心企业和配套企业，二者是产业链上下游关系，假定核心企业所在产业共有n个企业，配套企业所在产业共有m个企业。实际中核心企业可能只有1个，这不影响问题分析。垂直型产业集群式转移的动因是维持在转出地的非对称互惠共生系统，因此参与企业的收益和成本不对称。设C、D为代表性的核心企业和配套企业，若同时转移产生的Δπ增量利润核心企业获得aΔπ，而配套企业获得bΔπ。这里1/2＜a≤1，0＜b＜1/2，体现出非对称互惠共生系统能量分配的不对等性。核心企业单方面转移产生收益rc和成本cc，配套企业单方面转移产生收益rd和成本cd。核心企业因资产专用性带来的沉淀成本远超过配套企业，而配套企业经营柔性更容易根植嵌于承接地的产业体系。类似“智猪博弈”模型中“多劳不多得”现象，假定rc＜rd、cc＜cd，从而单方面转移相对净收益rd-cd＞rc-cc。同样假定因交易伙伴单方面转移给企业带来利润损失（搜寻新的交易伙伴的搜寻成本），对于核心企业是-πc，配套企业是-πd。图2给出了垂直型产业集群式转移博弈的收付矩阵，同样所列数据都是与转出地市场相比的净变动值。

图1　水平型集群式产业转移博弈收付矩阵

图2　垂直型集群式产业转移博弈收付矩阵

三、水平型集群式产业转移演化博弈分析

（一）水平型集群式产业转移演化博弈模型构建和均衡解

假定水平型集群式产业转移涉及产业中的q个企业有qtr个企业选择转移策略，占企业总数比重x=qtr/q，相应的1-x=（q-qtr）/q表示产业中未转移的企业比重。这里x和1-x都有双重含义，既能表示转移企业和未转移企业数占企业总数比重，也能表示具体某个企业的混合策略，即该企业以x的概率选择转移策略，以1-x的概率选择不转移策略。正是策略的双重含义，使得论文在分析集群产业中的企业演化博弈时，可以选取任何两个企业为代表。这也是演化博弈模型相比较于普通博弈模型的一个优点，在实践中对于一个具体企业要么选择转移，要么选择不转移，混合策略变得让人十分难以理解。而在演化博弈理论模型中，x除了表示参与人使用转移策略的概率，还可以理解成集群企业中参与转移的企业数所占比例，现实意义十分明显。结合图1水平型集群式产业转移博弈收付矩阵，下面给出企业A复制动态进化模型的推导过程，由于对称性原则，该过程对博弈另一方企业B也适用。

企业A选择转移的期望收益：

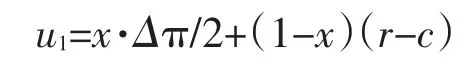
企业A选择不转移的期望收益：

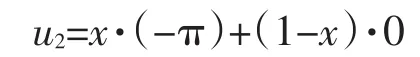
企业A的收益期望：

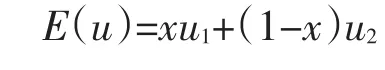
按照生物进化的复制动态思想，收益较低的企业会改变策略（严格地讲，是加大改变策略的概率），模仿高收益企业的策略，渐渐地集群内某种特定策略的成员比例就会发生变化，最终达到稳定状态的过程就是复制动态演化博弈过程。依据研究假设（2）群内企业采用某种特定策略比列的相对变化率（变化速度与其比重）和其收益超过期望收益的幅度成正比，以转移策略企业为例，上述问题中集群内采取转移策略的企业比例x的变化速度可用以下微分方程刻画：

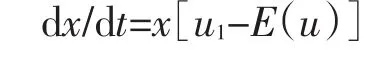
该复制动态方程的经济学含义是：采取转移策略的企业比例，其瞬时变化率与该类型企业的利益期望超过平均收益的差距成正比，也与该类型企业绝对数成正比。带入u1和E（u）的表达式化简整理得：

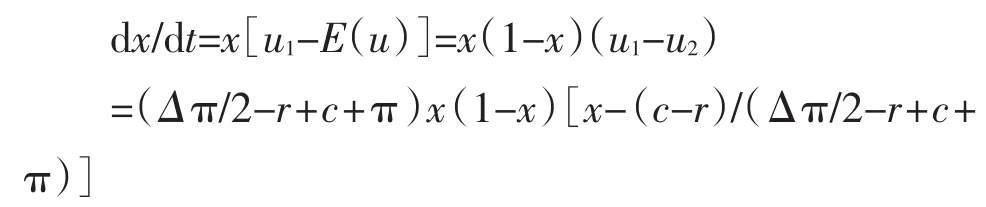
在演化博弈模型中，该微分方程又被称作复制动态方程，这里简记为F1（x）=dx/dt。令F1（x）=dx/dt= 0，可解得该复制动态方程的三个稳定点或不动点。

特别强调，复制动态方程的稳定点仅说明，一旦群体内采用转移策略企业的比例达到该水平后就不会发生变化，并不说明这些稳定点在复制动态博弈中一定都能实现，能否实现取决于稳定点左右微分方程值的变化方向。正如经济学强调均衡分析，但并不意味着均衡是常态，实际上更关注均衡一旦被破坏后系统是否有一种内在机制重新收敛回到均衡点。同样，演化博弈中的进化稳定策略（ESS）也必须具备对微小扰动的抗干扰性，一旦部分参与者因有限理性出现错误决策导致实际比例偏离某稳定点x*时，动态复制系统必须具备某种机制使系统重新收敛回到均衡点。为实现这一目标，要求当x以低于x*从左边偏离时，F（1x）=dx/dt＞0；当x以高于x*从右边偏离时，F（1x）=dx/dt＜0。要求稳定点处方程F（1x）的导数值F′（1x*）＜0，从几何上讲F（1x）图像与横轴交点处的切线斜率为负。

（二）水平型集群式产业转移条件和策略的稳定性分析

为了书写方便，这里记（c-r）（/Δπ/2-r+c+π）=ϕ，于是水平型集群式产业转移动态复制方程和导函数可改写成：

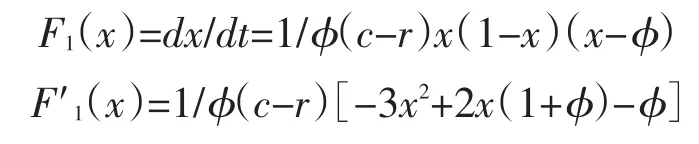
各稳定点处动态复制方程导数值与单方面转移的收益r与成本c的大小关系密切相关。由于r=c是特例不具备一般性，以下分r＞c和r＜c两种情况讨论水平型集群式产业转移条件和策略的稳定性。

（1）r＞c，即单方面转移收益超过成本，此时需进一步分为0＜r-c＜Δπ/2+π和r-c＞Δπ/2+π两种情况。

当0＜r-c＜Δπ/2+π时，ϕ＜0。将稳定点x1*=0，x2*=1，x3*=ϕ分别带入F′1（x）的表达式，F′1（0）=r-c＞0，F′1（1）=1/ϕ（c-r）（ϕ-1）＜0，F′1（ϕ）=（c-r）（1-ϕ）＜0。又ϕ＜0没有实际经济意义，故无须考察该点策略的稳定性。由进化稳定均衡的判定条件可知，此时x*=1是唯一的ESS。图3是0＜r-c＜Δπ/2+π时复制动态方程相位图。

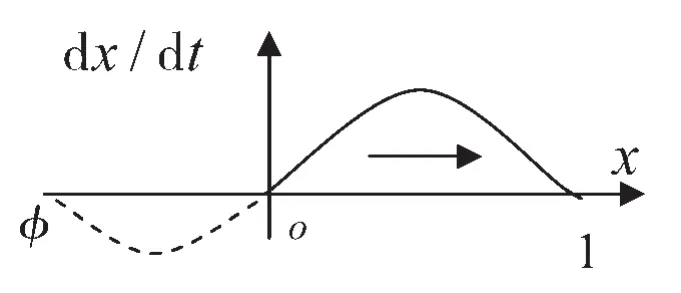
图3　0＜r-c＜Δπ/2+π时复制动态方程相位图

当r-c＞Δπ/2+π时，ϕ＞1。将稳定点x1*=0，x2*=1，x3*=ϕ分别带入F′1（x）的表达式F′1（0）=r-c＞0，F′1（1）=1/ϕ（c-r）（ϕ-1）＜0，F′1（ϕ）=（c-r）（1-ϕ）＞0。又ϕ＞1没有实际经济意义，故无须考察该点策略的稳定性。由进化稳定均衡的判定条件可知，此时x*=1同样是唯一的ESS。图4是r-c＞Δπ/2+π时复制动态方程相位图。

综合上述两种情况，只要企业单方面转移的收益r超过单方面转移产生的成本c，即r＞c时，水平型集群式产业转移复制动态演化博弈都只存在唯一的ESSx*=1，集群内所有企业选择转移。此时集群式产业转移十分容易实现，企业逐利的驱使最终演化成所有企业选择转移策略。事实上，在图1的博弈收付组合下，转移策略是每个参与人的上策，（dominantstrategy）（转移，转移）策略组合是该静态博弈的唯一上策均衡，这样在动态演化博弈中所有企业最终演化选择产业转移也就不难理解了。

图4　r-c＞Δπ/2+π时复制动态方程相位图

（2）r＜c，即单方面转移收益小于成本，此时0＜ϕ＜1。此时企业单方面转移的净收益为负，这比较符合我国现行产业转移的实际情况，至少在产业转移初期是这样。尽管承接地提供优厚的政策环境和低廉的要素成本为转移企业带来不少利益，但处在原对称互惠共生系统中的企业选择单方面转移也会因为外部规模不经济、知识的溢出效应等弱化带来的成本高于原共生环境的集聚作用时，就会出现单方面转移净收益为负的情况。

为了考察此时均衡点的稳定性，同样需要计算各均衡点在动态复制方程F1（x）导数值的符号。将稳定点x1*=0，x2*=1，x3*=ϕ分别带入F′1（x）的表达式F′1（0）=r-c＜0，F′1（1）=1/ϕ（c-r）（ϕ-1）＜0，F′1（ϕ）= （c-r）（1-ϕ）＞0。图5是r＜c时复制动态方程相位图。由动态复制方程在各稳定点导数值的符号和相位图与横轴交点处斜率，容易得出当企业单方面转移收益低于成本时，x*=0和x*=1是水平型集群式产业转移演化博弈的两个ESS，x*=ϕ是均衡点但并不是进化稳定均衡。策略x*=0意味着集群内没有任何企业选择转移，而x*=1意味着群内全部企业选择转移，亦即集群式产业转移能够实现。此时动态演化博弈的ESS有两个，究竟收敛于哪个均衡却不得而知，群内采取转移策略企业的初始比例大小直接影响博弈结果，结合图5来说明这一点。

当初始选择转移策略的企业比例为ϕ＜x＜1时，dx/dt＞0，转移企业所占比重超过一定规模后，类似于生物进化的正反馈效应起主要作用。企业产业转移后效益明显，对群内未转移的其他企业示范效应增强，转移企业种群数量将持续递增，以1-ϕ的概率收敛于进化稳定策略x=1处，只要时间充足，群内所有企业都会选择转移；当初始选择转移策略的企业比例为0＜x＜ϕ时，dx/dt＜0，转移企业所占比重小于一定规模，类似于生物进化的负反馈效应起主要作用。由于企业转移后绩效甚微，对群内未转移的其他企业威慑效应增强，不转移企业种群数量将持续递增，以ϕ的概率收敛于进化稳定策略x=0处，也就是说，群内所有企业都选择不转移。由此可见，当企业单方面转移收益低于成本时，存在一个转移企业比例的初始临界水平ϕ，在该水平以上，企业复制动态变化的结果趋向全部转移，水平型集群式产业转移能够实现；而在该水平以下，集群式产业转移不能实现。

图5　r＜c时复制动态方程相位图

综上所述，可得到水平型集群式产业转移条件及稳定性以下命题。

命题1：在水平型集群式产业转移过程中，若企业单方面转移收益超过成本，集群式产业转移是自由市场的内生结果。更多情形下企业单方面转移收益低于成本，复制动态演化博弈存在两个ESS，分别是x*=0和x*=1，博弈初始时的转移企业所占比重直接决定了稳定均衡的走向。存在一个临界水平ϕ，在该水平以上，水平型集群式产业转移能够实现；而在该水平以下，集群式产业转移不能实现。

四、垂直型集群式产业转移演化博弈分析

（一）垂直型集群式产业转移演化博弈模型构建和均衡解

垂直型集群式产业转移是产业链带动下的核心企业带动配套企业的产业整体转移，配套企业从属于核心企业，分工以垂直分工为主，在原共生系统中处于非对称互惠共生模式。垂直型集群式产业转移在实践中更具有一般性，其转移利益主要是源于产业集群在资源配置上能综合市场和科层组织的优势。理论上讲，水平型集群式产业转移参与企业的博弈在同一产业内部企业之间进行，企业转移决策是尽可能维持原对称共生系统因集聚效应带来的外部规模经济。而垂直型集群式产业转移的参与企业既可能是同一产业内部，也可能是同一产业链上下游企业之间的博弈，企业转移决策除了维持因集聚效应带来的外部规模经济，更重要的是，单方面转移必然给企业带来因搜寻新交易伙伴的高昂交易成本，垂直型集群式产业转移的条件和稳定性的分析也因此变得复杂得多。

假定核心企业所在产业的m个企业有mtr个企业选择转移策略，占产业企业总数比重x=mtr/m，相应地1-x=（m-mt）r/m表示产业中未转移的企业比重。如果核心企业只有一个，x和1-x分别表示核心企业选择转移和不转移策略的概率。配套企业所在产业的n个企业有ntr个企业选择转移策略，占产业企业总数比重y=ntr/n，相应地1-y=（n-ntr）/n表示产业中未转移的企业比重。同前文一样，这里转移策略都有双重含义，既能表示转移企业数和未转移企业数占产业企业总数比重，又能表示具体某个企业的混合策略。

1.核心企业动态复制演化博弈分析

结合图2垂直型集群式产业转移博弈收付矩阵，可计算：

企业C选择转移的期望收益：u1=yaΔπ+（1-y）（rc-cc）

企业C选择不转移的期望收益：u2=y·（-πc）+（1-y）·0

企业C的收益期望：E（u）=xu1+（1-x）u2

核心企业的复制动态方程：dx/dt=x［u1-E（u）］=x（1-x）（u1-u2）=（aΔπ+πc+cc-rc）x（1-x）［y-（cc-rc）/（aΔπ+πc+cc-rc）］

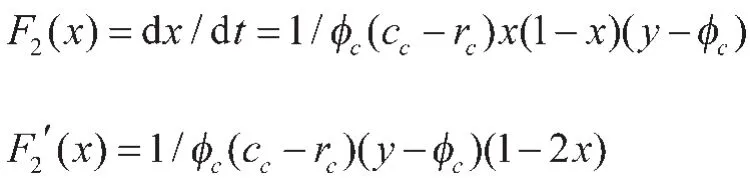
2.配套企业动态复制演化博弈分析

企业D选择转移的期望收益：v1=xbΔπ+（1-x）（rd-cd）

企业D选择不转移的期望收益：v2=x·（-πd）+（1-x）·0

企业D的收益期望：E（v）=yu1+（1-y）v2

配套企业的复制动态方程：dy/dt=y［v1-E（v）］=y（1-y）（v1-v2）=（bΔπ+πd+cd-rd）y（1-y）［x-（cd-rd）/（bΔπ+πd+cd-rd）］

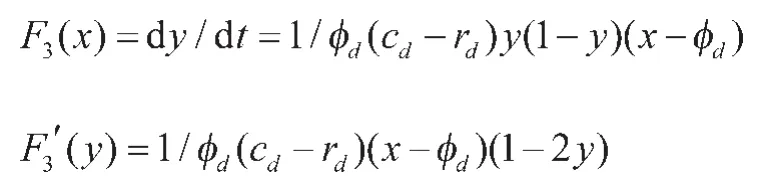
（二）垂直型集群式产业转移条件和策略的稳定性分析

在重复博弈中，最优的均衡策略能够经受住有限理性所引起的错误与偏离的干扰，在遭受干扰后仍能恢复，该均衡才能被视作ESS。为检验上述复制动态方程两个稳定点是否具有对微小偏离的抗干扰性，首先考察F（2x）在均衡点处的数学性性态。一种极端的情形是当y=ϕc时，则任意的x∈［0，1］皆为稳定状态，这在实践中很难去解释，下面分析更一般的y≠ϕc的情况。

1.核心企业转移条件和进化稳定性分析

当rc＜cc时，核心企业单方面转移收益小于成本，在转移初期比较常见，此时0＜ϕc＜1。当y＜ϕc时，如果配套企业转移比例小于某一临界值，核心企业复制演化博弈均衡收敛于x*=0不转移。图6是rc＜cc，y＜ϕc时核心企业复制动态方程相位图。

图6　rc＜cc，y＜ϕc时核心企业复制动态方程相位图

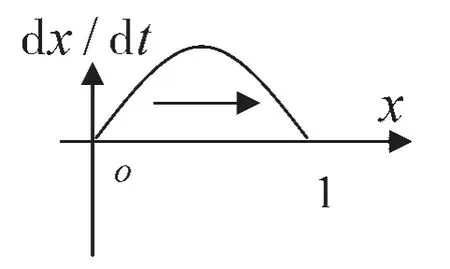
图7　rc＜cc，ϕc＜y≤1时核心企业复制动态方程相位图

核心企业单方面转移收益低于成本时，其转移策略决定于交易伙伴配套企业转移的比例。当配套企业转移比例小于某一临界值，核心企业复制演化博弈均衡收敛于x*=0不转移；当配套企业转移比例大于某一临界值，核心企业复制演化博弈均衡收敛于x*=1选择转移。

当rc＞cc时，核心企业单方面转移收益大于成本，这在产业转移中后期比较常见，此时核心企业单方面转移收益与成本差距影响均衡和策略的稳定性。

rc-cc＞aΔπ+πc时，核心企业单方面转移净收益超过某一水平。容易看出ϕc＞1，显然也有y＜ϕc。图8是rc-cc＞aΔπ+πc时核心企业复制动态方程相位图。

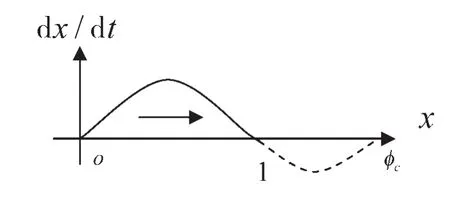
图8　rc-cc＞aΔπ+πc时核心企业复制动态方程相位图

当0＜rc-cc＜aΔπ+πc时，核心企业单方面转移净收益为正但低于某一水平。此时图9是0＜rc-cc＜aΔπ+πc时核心企业复制动态方程相位图。

图9　0＜rc-cc＜aΔπ+πc时核心企业复制动态方程相位图

概括起来，只要核心企业单方面转移的净收益为正，核心企业复制演化博弈均衡收敛于x*=1选择转移。

2.配套企业转移条件和进化稳定性分析

配套企业转移条件和进化稳定性分析情形与核心企业推导过程相似。一种极端的情形是当x=ϕd时，则任意的y∈［0，1］皆为稳定状态，这在实践中很难去解释，下面分析更一般的x≠ϕd的情况。当rd＜cd时，配套企业单方面转移收益小于成本，此时0＜ϕc＜1。

x＜ϕc时，F′（30）=1/ϕ（dcd-rd）（x-ϕd）＜0，F′（31）=-1/d（cd-rd）（x-ϕd）＞0。图10是rd＜cd，x＜ϕd时配套企业复制动态方程相位图。

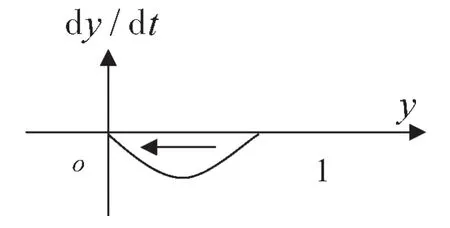
图10　rd＜cd，x＜ϕd时配套企业复制动态方程相位图

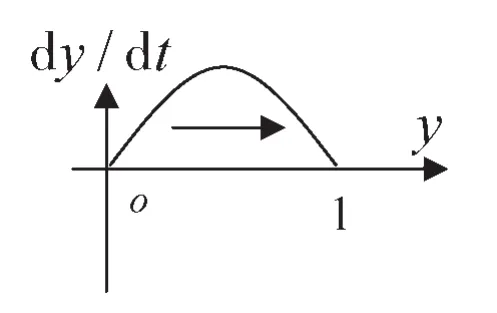
图11　rd＜cd，ϕd＜x≤1时配套企业复制动态方程相位图

配套企业单方面转移收益低于成本时，其转移策略决定于交易伙伴核心企业转移的概率（或比例）。当核心企业转移概率（或比例）小于某一临界值，配套企业复制演化博弈均衡收敛于y*=0不转移；当核心企业转移概率（或比例）大于某一临界值，配套企业复制演化博弈均衡收敛于y*=1选择转移。

当rd＞cd时，配套企业单方面转移收益大于成本。rd-cd＞bΔπ+πd时，配套企业单方面转移净收益超过某一水平。容易看出ϕd＞1，显然也有x＜ϕd。图12是rd-cd＞bΔπ+πd时配套企业复制动态方程相位图。

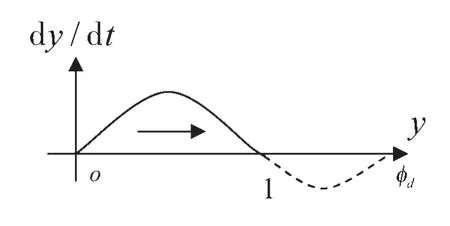
图12　rd-cd＞bΔπ+πd时配套企业复制动态方程相位图

0＜rd-cd＜bΔπ+πd时，配套企业单方面转移净收益为正但低于某一水平。此时图13是0＜rd-cd＜bΔπ+πd时配套企业复制动态方程相位图。

图13　0＜rd-cd＜bΔπ+πd时配套企业复制动态方程相位图

概括起来，只要配套企业单方面转移的净收益为正，配套企业复制演化博弈均衡收敛于y*=1选择转移。

综上所述，可得到垂直型集群式产业转移条件及稳定性以下命题。

命题2：在垂直型集群式产业转移过程中，只要核心企业和配套企业单方面转移收益都超过成本，集群式产业转移是自由市场的内生必然结果。更一般的情形下企业单方面转移收益低于成本，此时交易伙伴的转移比例（或概率）决定着复制动态演化博弈均衡的走向。对于核心企业和配套企业都存在一个临界水平，只有核心企业和配套企业的转移比例（或概率）都达到该水平以上，垂直型集群式产业转移才能顺利实现。

五、引入政府干预后对集群式产业转移的影响

以上用生态行为学的复制动态模型对水平型和垂直型集群式产业转移的讨论，是在没有政府干预完全自由的市场上，企业基于经济理性的自发选择结果，没有考虑产业转移过程中政府作为第三方力量其行为对企业策略选择的影响。事实上，政府主导下的产业转移成为目前我国产业转移的主要形式。以下引入政府，考虑增加转移企业的收益和减少转移企业成本两个因素下，集群式产业转移形成条件、成功概率有什么变化。前文分析已经得出，无论是水平型产业转移还是垂直型产业转移，只要企业转移预期收益超过成本，集群式产业转移是市场自然选择的内生必然结果。在这种情况下，政府的干预就没有必要，鉴于垂直型集群式产业转移在实践中更具有普遍性，下面对引入政府干预后对集群式产业转移的影响只分析垂直型产业转移且企业单方面转移收益低于成本的情形。

（一）垂直型集群式产业转移概率的影响因素

显然集群式产业转移要求核心企业和配套企业群同时转移，二者转移概率共同影响垂直型产业转移顺利实施的概率。将图6、图7、图10和图11置于以核心企业转移概率x（或比例）为横轴，配套企业转移比例y为纵轴的坐标平面中。如图14所示，当博弈初始状态落入区域Ⅰ时，双方选择转移策略的比例（或概率）都小于某一正值，演化博弈均衡收敛于ESS O（x=0，y=0），不能实现集群式产业转移。而当博弈初始状态落入区域Ⅱ或者区域Ⅳ时，演化博弈的均衡是不确定的，这主要取决于博弈一方的成功程度与另一方的学习模仿速度。当且仅当双方选择转移策略的比例（或概率）高于某一正值落入区域Ⅲ时，演化博弈均衡收敛于ESS E（x=1，y=1），集群式产业转移最终得以实现。

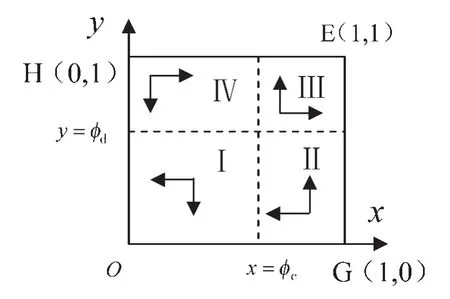
图14　垂直型集群式产业转移实施概率分布图

如果把企业选择转移视为随机事件，该随机变量x和y服从［0，1］的均匀分布，再假定核心企业和配套企业选择转移为相互独立事件，这样P（x=1，y= 1）=P（x=1）·P（y=1）。注意到正方形框的面积为1，于是集群式产业转移顺利实施的概率P刚好等于区域Ⅲ的面积（1-ϕd）（1-ϕc），计算化简得：

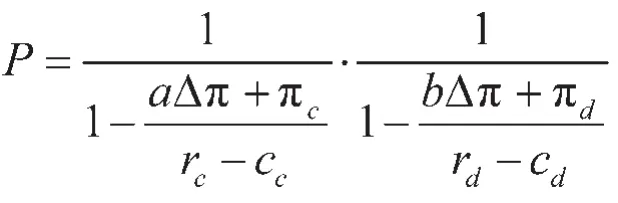
由上式可以看出，影响集群式产业转移成功实施概率的因素有同时转移产生的Δπ、单方面转移的收益和成本、利润分配比例等。其中利润分配比例一般由产业链上下游企业竞争关系确定，P解析式构成直观地给出了政府促进产业集群式转移的政策方向。政府促进集群式产业转移顺利实施的概率既可以增加企业的转移收益r，也可以减少转移成本c，二者都可增加转移企业的转移净收益。

（二）政府干预对垂直型集群式产业转移顺利实施概率的影响

已经明确政府促进集群式产业转移顺利实施的概率既可以增加企业的转移收益，也可以是减少转移成本。由于二者作用机理类似，下面以增加转移企业收益讨论政府干预对垂直型集群式产业转移顺利实施概率的影响。

从ϕc和ϕd的代数形式可以看出，政府对核心企业和配套企业增加转移收益或者减少转移成本，都可以降低ϕc和ϕd的数值，命题2已经表明ϕc和ϕd分别是核心企业和配套企业演化博弈均衡收敛方向的临界点。政府对集群内转移企业的干预，无论是增加转移收益还是减少转移成本，都可以增加集群式产业转移的成功概率P。从图15直观上看，细虚线代表政府干预前的临界值，粗实线代表干预后的临界值，政策带来的转移收益增加了区域Ⅲ的面积，亦即加大垂直型集群式产业转移顺利实施概率。

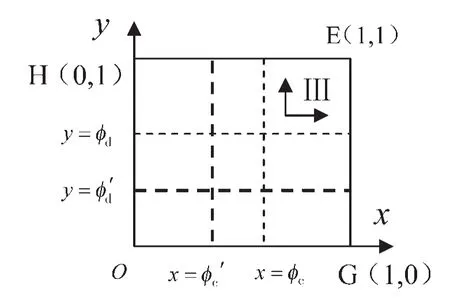
图15　政府干预对垂直型集群式产业转移实施概率影响

（三）两种不同的政府干预思路

以上对垂直型集群式产业转移的分析所有结论对核心企业和配套企业是对称的，似乎二者具有同等的重要性。事实上政府对核心企业和配套企业同等程度的补贴对集群式产业转移成功概率的提升程度并不相同，实践中对应着两种完全不同的政策干预思路。一种是承接地政府“抓大放小”，重点采取各种优惠政策让产业链核心企业落户，集群内原配套企业的产业转移完全是市场行为；另一种是承接地政府“筑巢引凤”，采取各种优惠政策吸引配套企业先落户，或者鼓励地方积极兴办配套产业增强产业转移的根植性，利用良好的发展环境诱使核心企业产业转移。由此产生一个重要问题，政府因为自身预算约束的存在，同等程度的政策优惠给核心企业还是配套企业对集群式产业转移成功实施的概率提高哪个更大？显然这个问题的回答尤其重要，它直接影响实际产业转移中“抓大放小”和“筑巢引凤”哪种模式更具有可行性。

回答这个问题只需对集群式产业转移实施概率P对核心企业和配套企业利润分配比例a和b分别求导，比较同等程度的利润变动对实施概率P的影响大小即可。

经计算：

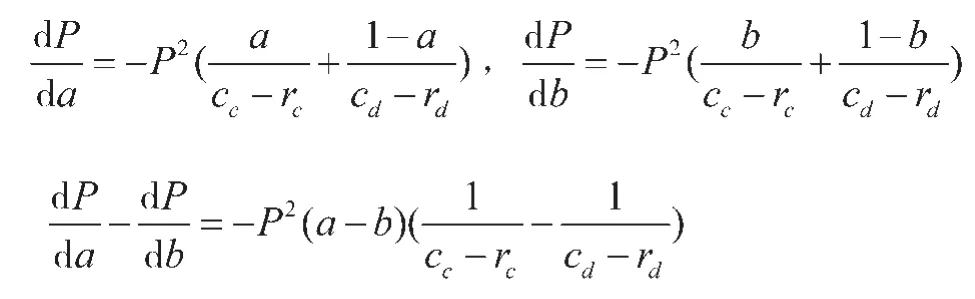
由本文假设，a∈（1/2，1），b∈（1，1/2），rc＜rd、因此同等程度的政策优惠给核心企业对集群式产业转移成功实施的概率影响更大。

命题3：政府的干预，无论是增加转移收益还是减少转移成本，虽然不能确保集群式产业转移，但由于临界值水平的下降增加了集群式产业转移的成功概率。在垂直型集群式产业转移过程中，政府同等程度的政策优惠给核心企业对集群式产业转移成功实施的概率影响更大。

六、研究启示

本文基于演化博弈理论视角对水平型和垂直型两种情形下集群式产业转移的条件及稳定性进行研究，论文主要研究结论对我国正在实施的集群式承接产业转移有重要启示意义。

第一，无论是水平型还是垂直型集群式产业转移，只要企业单方面转移收益超过成本，集群式产业转移是市场机制的内生必然结果。为了成功实现产业集群式转移，政府的各种干预政策仅当企业单方面转移收益低于成本时才有必要。在我国的产业转移实践中，尽管中西部地区承接地地方政府为转移企业提供优厚的政策优惠、配套硬软件环境，但至少在转移初期因合作交易伙伴没有及时跟随转移导致外部规模不经济和交易费用增加，最终使得企业单方面转移净收益往往小于0。这既为地方政府干预产业转移提供理论基础，同时也阐明了政策方向。本文的研究表明，尽管政府的干预，无论是增加转移收益还是减少转移成本，虽然不能确保集群式产业转移一定能够顺利实施，但政府干预降低集群式产业转移所要求的交易伙伴转移率的临界值水平，至少可以增加集群式产业转移成功的可能性。

第二，借力集群式承接产业转移，可破解产业转移过程中的区域黏性。在产业梯度转移过程中，企业置身的生产关系网络和社会关系网络对产业转移产生阻力，使得产业转移不能按照区域梯度循序进行，称作产业转移区域黏性，也有学者称之为根植性。而集群式承接产业转移可破解产业转移过程中的地方根植性，为承接地政府化解产业转移区域黏性提供政策方向。就企业转移决策的影响而言，生产关系网络和社会关系网络却是密不可分，二者是互补关系而不是替代关系，并一起成为产业转移区域黏性的影响因素。集群式承接产业转移首先可以维持企业在原产地早已形成的共生网络关系。这种共生网络关系实际上就是生产网络关系，于是借助集群式产业转移可以化解因生产关系网络破坏形成的产业转移阻力。企业对生产关系网络维系的关系投资，在承接地仍然为企业带来收益流。其次，通过产业园区协调和政府行政配套改革，集群式承接产业转移可以尽可能维持企业在原产地的社会关系网络。其中，社会关系网络中以亲缘为纽带的关系投资可随集群式产业转移在承接地继续维系，而对转出地政府机构的关系投资无法在承接地继续发挥作用。承接地政府需要进一步精简行政审批程序，提高办事效率，努力实现政府从管理角色向服务角色的转变。同时产业园区管委会注意做好转移企业与地方政府的协调工作，重新搭建企业与地方政府基于信任基础上的社会关系网络，将社会关系网络对产业转移黏性的影响降到最低。

第三，在我国产业转移实践中，普遍存在“重增加收益，轻减少成本”现象，表现在承接地政府有足够激励且竭尽所能的为转移企业提供各种可能的税收、土地和财政等政策优惠，而转出地政府减小企业的转移成本缺乏应有的经济激励。论文从理论上已经证明，就提高集群式产业转移成功概率这一目标的政策手段上看，承接地政府增加转移收益和转出地政府减小转移成本具有同等功效。转出地政府减小企业的迁移成本也有多种手段，如对资产允许企业采取加速折旧的会计处理、合理安置企业因迁移而分流的人员、为实现产业结构高级化直接对特定产业的企业转出适当补偿等。这些手段都可以增加企业转移净利润，稳定企业预期，增强它们在承接地经营企业的信念。更为重要的是，这种信念在集群内产生模仿和示范效应，类似于生物进化的正反馈效应得到加强，有利于尽早达到集群式产业转移对交易伙伴转移比例的临界值水平。应尽快健全承接地政府和转出地政府的协调机制，既发挥承接地政府增加转移收益对企业转移拉力作用，又要利用转出地政府减小转移成本对转移企业形成推力作用，使二者发生合力，集群式产业转移才能最终得以顺利进行。

最后，政府自身的预算约束使其对政策本身也有成本，政府需要在“抓大放小”和“筑巢引凤”两种模式中取优。“抓大放小”模式中承接地方政府重点采取各种优惠政策让产业链核心企业落户，配套企业的产业转移完全是市场行为。“筑巢引凤”模式中承接地政府各种优惠政策吸引配套企业落户，营造良好的发展环境诱使核心企业产业转移。本文分析得出同等程度的政策优惠给核心企业对集群式产业转移成功实施的概率影响更大，这表明“抓大放小”模式鼓励产业集群式转移在现实经济中更具有可行性。考虑到配套企业数量多和财政压力矛盾、鼓励核心企业落户后发展地方配套产业能增强产业的根植性等这些因素后，“抓大放下”模式就显得更有必要。

［1］刘友金，胡黎明，赵瑞霞.基于产品内分工的国际产业转移新趋势研究动态［J］.经济学动态，2011，（3）.

［2］魏后凯.产业转移的发展趋势及其对竞争力的影响［J］.福建论坛，2003，（4）.

［3］刘友金，袁祖凤，易秋平.共生理论视角下集群式产业转移演化博弈分析［J］.系统工程，2012，（2）.

［4］Ltwontin R C.Evolution and the Theory of Games ［J］.Journal of Theoretical Biology，1960，（1）.

［5］Smith M J，Price G R.The Logic of Animal Conflicts［J］.Nature，1973，（246）.

A Study of Industrial Clustering Transfer Model Choice Based on Evolutionary Game Theory

Li Ting

Thepaperregardsindustrialclusteringtransferasaprocessof“groupdecisionmaking，adjustmentand stabilization”between bounded rationality enterprises.The paper studies horizontal and vertical industrial transfer condition and stability based on evolutionary game model.The government’s intervention，both increasing transfer income or reducing transfer cost，can not ensure clustering industrial transfer，but decreased“critical level”can increase the success probability of clustering industrial transfer.Under vertical industrial transfer the government’s same subsidies to core enterprise will have higher possibility of clustering industrial transfer successfully.The paper proves that“catching big throwing small”mode has more feasibility than“building nest to attract phoenix”mode at present stage.

Evolutionary Game；Industrial Clustering Transfer；Evolutionarily Stable Strategy；Transfer Condition；Stability

F427

A

2095—5766（2016）05—0120—10

2016—07—15

安徽省哲学社会科学规划项目“基于演化博弈理论的皖江城市带集群式承接产业转移机理及对策研究”（AHSKY2014D58）。

李停，男，铜陵学院经济学院副教授，经济学博士（铜陵244000）。

（责任编辑：文锐）