On Pseudo Weakly Clean Rings
2016-10-17HAOYapuCHENHuanyin
HAO Yapu, CHEN Huanyin
(School of Science, Hangzhou Normal University, Hangzhou 310036, China)
On Pseudo Weakly Clean Rings
HAO Yapu, CHEN Huanyin
(School of Science, Hangzhou Normal University, Hangzhou 310036, China)
A ringRis called a pseudo weakly clean ring if every elementx∈Rcan be written in the form ofx=e+u+(1-e)rxorx=-e+u+(1-e)rxwhereeis an idempotent anduis a invertible element. These rings are shown to be a unifying generalization of skew power series ringR[[x;σ]], Hurwitz series ringH(R) andT(R,σ). The pseudo weak cleanness of the ring of triangular matrices is discussed as well. Furthermore, this paper proves that the following are equivalent: that isRis pseudo weakly clean; there is an integernsuch thatR[x]/(xn) is pseudo weakly clean; there is an integernsuch thatR[[x]]/(xn) is pseudo weakly clean.
pseudo weakly clean ring; skew power series ring; Hurwitz series ring; Weakly exchange ring; ideal.
Article ID: 1674-232X(2016)05-0514-08
1 Introduction
A ringRis said to be pseudo clean if for everyx∈Rthere exist an idempotente∈Rand a unitu∈Rsuch thatx-e-u∈(1-e)Rx[1]. An elementx∈Ris pseudo weakly clean if there exist an idempotente∈Rand a unitu∈Rsuch thatx-e-u∈(1-e)Rxorx+e-u∈(1-e)Rx. A ringRis said to be pseudo weakly clean if every element inRis pseudo weakly clean[2]. Pseudo clean rings are clearly pseudo weakly clean. However, a pseudo weakly clean ring may be not necessarily pseudo clean (see [2, Example 3.2.1]). We shall prove that an abelian ringRis pseudo weakly clean if and only ifRis pseudo clean.
We shall explore further properties of pseudo weakly clean rings. These rings are shown to be a unifying generalization of skew power series ringR[[x;σ]], Hurwitz series ringH(R) andT(R,σ). The pseudo weak cleanness of the ring of triangular matrices is discussed as well. Furthermore, we prove that the following are equivalent:Ris pseudo weakly clean; there is an integernsuch thatR[x]/(xn) is pseudo weakly clean; there is an integernsuch thatR[[x]]/(xn) is pseudo weakly clean.
Throughout, all rings will be associative with an identity, unless otherwise specified. The symbolsC(R),Id(R),U(R),Mn(R) andTn(R) will stand for the set of all centers, the set of all idempotents, the set of all units, the ring ofn×nmatrices and the ring of alln×nupper triangular matrices overR, respectively.
2 Equivalent Characterizations
Following Tat, an elementxof a ringRis pseudo weakly clean in case there exist an idempotente∈Rand a unitu∈Rsuch thatx-e-u∈(1-e)Rxorx+e-u∈(1-e)Rx([2]).
The following assertion is useful for applications.
Lemma 1Every homomorphic image of a pseudo weakly clean ring is pseudo weakly clean.
ProofSee [2, Proposition 3.4.1].
□
Letσbe an endomorphism ofR. We denote the skew formal power series ring
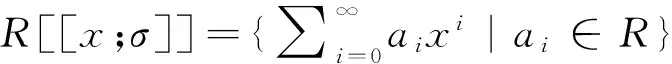
where addition is naturally defined and multiplication is defined by using the relationxb=σ(b)xfor allb∈R. In particular,R[[x]]=R[[x;1R]] is the ring of power series overR.
Lemma 2For any ringR, the skew power seriesfis a unit inR[[x;σ]] if and only iff(0) is a unit inR.
ProofSee [3, Lemma 4].
□
Theorem 1LetRbe a ring. ThenRis pseudo weakly clean if and only if so isR[[x;σ]].
ProofSuppose thatRis pseudo weakly clean, for anya∈R, we havea=e+u+(1-e)r(x) ora=-e+u+(1-e)r(x) wheree∈Id(R) andu∈U(R). Ifa=e+u+(1-e)r(x), thenf(x)=a0+a1x+a2x2…=e+u+(1-e)ra0+(a1x+a2x2+…)=e+u+(a1x+a2x2+…)-(1-e)r(a1x+a2x2+…)+(1-e)rf(x)=e+α(x)+(1-e)rf(x). Similarly, ifa=-e+u+(1-e)r(x), thenf(x)=-e+α(x)+(1-e)rf(x). It is easy to knowα(x)∈U(R[[x;σ]]), hence,R[[x;σ]] is pseudo weakly clean.
Conversely, suppose thatR[[x;σ]] is pseudo weakly clean. Then it follows by the isomorphismR≅R[[x;σ]]/(x) thatRis pseudo weakly clean.
□
By [2, Proposition 3.4.8], the ringR[[x]] of all power series over commutative pseudo weakly clean ringRis pseudo weakly clean. We now extend this fact to noncommutative case.
Theorem 2LetRbe a ring. ThenRis pseudo weakly clean if and only if so isR[[x]].
ProofChooseσ=1Rin Theorem 1, the result immediately follows.
□
Corollary 1LetRbe a ring.R[[x1,…,xn]] is pseudo weakly clean if and only if so isR.
ProofBy Theorem 2 and induction, we easily obtain.
□

Lemma 3LetRbe a ring. Then the Hurwitz seriesx=(x0,x1,x2,…) is a unit inH(R) if and only ifx0is a unit inR.
ProofSee [4, Lemma 3.2].
□
Theorem 3LetRbe a ring. ThenRis pseudo weakly clean if and only if so isH(R).
ProofEvery homomorphic image of a pseudo weakly clean ring is pseudo weakly clean by Lemma 1, soR≅H(R)/kerφis pseudo weakly clean, whereφ:H(R)→R.
Conversely, suppose thatRis pseudo weakly clean. Letx=(xn)∈H(R). Thenx0∈R. Hence,x0=e+u′+(1-e)rx0orx0=-e+u′+(1-e)rx0fore∈Id(R) andu′∈U(R). Thusx=λR(e)+u+λR[(1-e)rx]=(e,0,0,…)+u+((1-e)rx,0,0,…) orx=-λR(e)+u+λR[(1-e)rx]=-(e,0,0,…)+u+((1-e)rx,0,0,…), whereu∈U(H(R)).
□
Theorem 4LetRbe a ring. Then the following are equivalent:
(1)Ris pseudo clean ring;
(2)T2(R) is pseudo weakly clean ring;
(3)Tn(R) is pseudo weakly clean ring for somen∈N*;
(4)Tn(R)ispseudoweaklycleanringforalln∈N*.
or

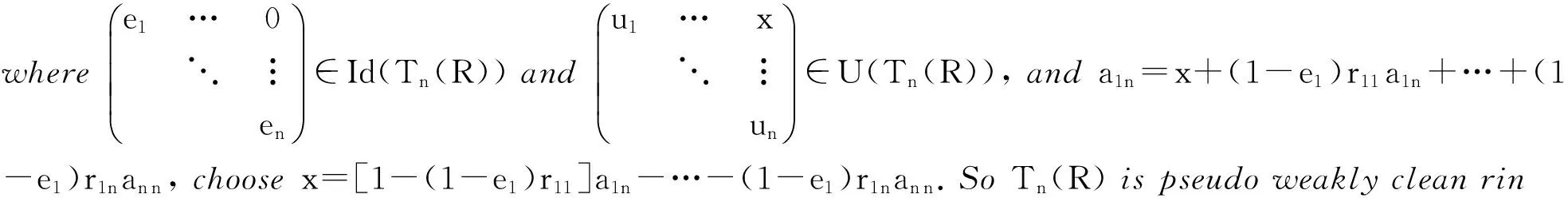
(4)⟹(3) It is obvious.
(3)⟹(2) T2(R)isasubringofTn(R),sotheresultimmediatelyfollows.
□
Theorem 5LetRbe a ring and letn∈N*.Thenthefollowingareequivalent:
(1)Rispseudoweaklyclean;
(2)R[x]/(xn)ispseudoweaklyclean;
(3)R[[x]]/(xn)ispseudoweaklyclean.
Proof(1)⟹(2) Suppose thatRis pseudo weakly clean, for anya∈R, we havea=e+u+(1-e)r(x) ora=-e+u+(1-e)r(x) wheree∈Id(R) andu∈U(R). Ifa=e+u+(1-e)r(x), thenR[x]/(xn)=a0+a1x++a2x2…+an-1xn-1=e+u+(1-e)ra0+(a1x+a2x2+…+an-1xn-1)=e+u+(a1x+a2x2+…+an-1xn-1)-(1-e)r(a1x+a2x2+…+an-1xn-1)+(1-e)rR[x]/(xn)=e+α(x)+(1-e)rR[x]/(xn). Similarly, ifa=-e+u+(1-e)r(x), thenR[x]/(xn)=-e+α(x)+(1-e)rR[x]/(xn). It is easy to knowα(x)∈U(R[x]/(xn)), hence,R[x]/(xn) is pseudo weakly clean.
(2)⟹(3) It is obvious.
(3)⟹(1) By Theorem 2.
□
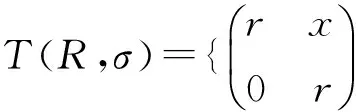
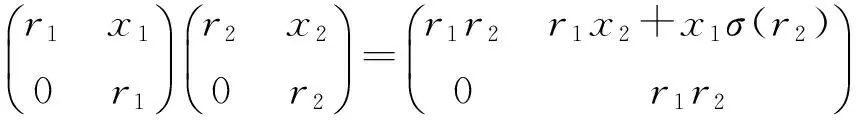
In particular, ifσ=1R, thenT(R,σ)=T(R,R).
Theorem 6LetRbe a ring. ThenRis pseudo weakly clean if and only if so isT(R,σ).

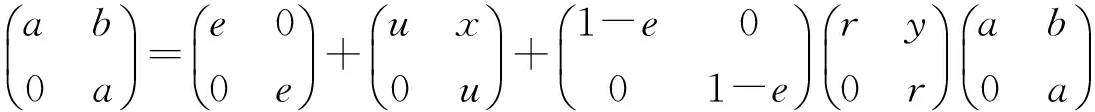
or
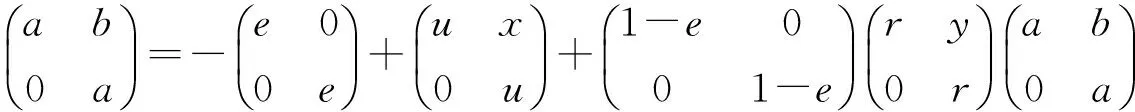
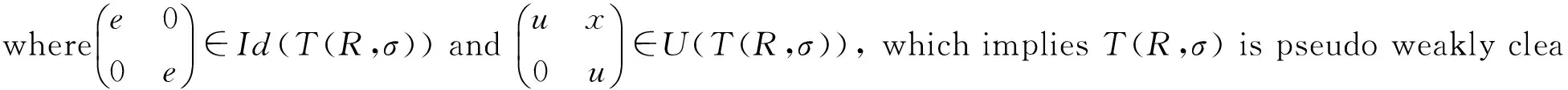

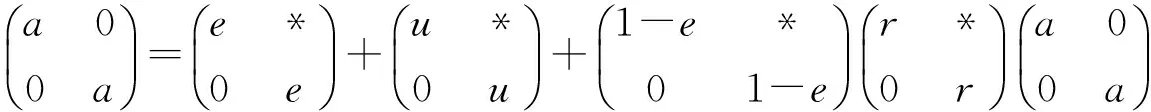
or
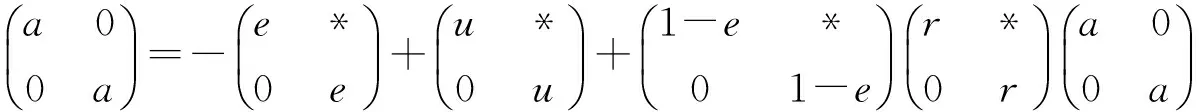

□

Corollary 2LetRbe a ring, and letMbe anR-R-bimodule. ThenRis pseudo weakly clean if and only if so isT(R,M).
ProofChooseσ=1Rin Theorem 6, the result immediately follows.
□
3 Related Rings
A ringRis said to be abelian if all of its idempotents are central. An elementxofRis called weakly exchange if there existse∈Id(R) such thate∈xRand 1-e∈(1-x)Ror 1-e∈(1+x)R. The ringRis said to be weakly exchange if every element is weakly exchange.
Proposition 1LetRbe an abelian ring. ThenRis weakly exchange if and only ifRis pseudo weakly clean.
ProofBy [2, Theorem 3.3.1] and [5, Theorem 2.2].
□
A ringRis called weakly-Abel ifeR(1-e)⊆J(R) for eache∈Id(R). Clearly, Abelian rings are weakly-Abel, but the converse is not true by the following example.
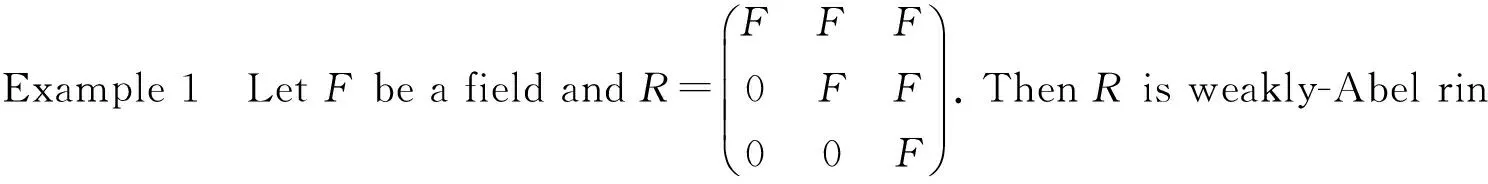

Following Wei and Li[7], a ringRis called weakly normal if for alla,r∈Rande∈Id(R),ae=0 impliesRerais nil left ideal ofR. Clearly, weakly normal rings are abelian.
Corollary 3(1) LetRbe a quasi-normal ring or weakly normal ring. ThenRis a pseudo weakly clean ring if and only ifRis a weakly exchange ring.
(2) LetRbe a ring. IfU(R)⊆C(R), thenRis a pseudo weakly clean ring if and only ifRis a weakly exchange ring.
Proof(1) It is obvious.
(2) By Proposition 1 and [2, Lemma 2.3.5].
□
Proposition 2LetRbe a pseudo weakly clean ring. IfRis an abelian ring, for every elementx, their existe,uinRsuch thatx-e-u∈(1-e)Rxif and only if for every elementx, their existe,uinRsuch thatx-e-u∈xR(1-e).
ProofIn the caseRis an abelian ring, a pseudo weakly clean ring is weakly exchange by Proposition 1. So 1-e=(1-x)ror 1-e=(1+x)r, andx-e-u=(1-e)rx,x-(1-e)rx=e+u, [1-(1-e)r]x=e+u. This shows that [1-(1-x)r2]x=x[1-r(1-x)r]=x[1-r(1-e)]=e+u, sox-e-u=xr(1-e), as required.
Conversely, writex-e-u=xr(1-e),x-xr(1-e)=e+u,x[1-r(1-e)]=e+u. This shows thatx[1-r(1-x)r]=[1-(1-x)r2]x=[1-(1-e)r]x=e+u,x-e-u=(1-e)rx, sox-e-u∈(1-e)Rx.
□
LetRbe a ring. We say thatRis a uniquely pseudo weakly clean ring, ifRis a pseudo weakly clean ring and for every elementx∈Rthe following hold:
(a)Ifx=u+e+(1-e)rxfor someu∈U(R) ande∈Id(R), then this representation is unique;
(b)Ifx=u-e+(1-e)rxfor someu∈U(R) ande∈Id(R), then this representation is unique.
Proposition 3LetRbe a uniquely pseudo weakly clean ring. ThenRis abelian.
ProofSupposeRis uniquely pseudo weakly clean, then
a:=[e+er(1-e)]+1+{1-[e+er(1-e)]}·0·a=e+[1+er(1-e)]+(1-e)·0·a
or
a:=-[e+er(1-e)]+1+{1-[e+er(1-e)]}·0·a=-e+[1-er(1-e)]+(1-e)·0·a
wheree∈Id(R) andr∈R. Letf=e+er(1-e), it is obviousf∈Id(R). Soe=e+er(1-e), this shows thater=ere. Similarly,re=ere. Soer=re. Thus,Ris abelian.
□
Recall that ifRis a (unital) ring,e∈Ran idempotent andIan ideal ofR, theneIe={exe|x∈I} is an ideal of the corner ringeRe.
In the sequel, by a non-unital ring we mean an associative ring without identity. In [8], Ster introduced the notion of a pseudo clean non-unital ring. In [2], Tat extended the notion of pseudo cleanness in non-unital ring to that of pseudo weakly cleanness. LetIbe a non-unital ring. LetQ(I)={p∈I|∃p′∈Isuch thatp+p′+p′p} and letQ′(I)={q∈I|∃q′∈Isuch thatq-q′+qq′=0=q-q′+q′q}. An elementx∈Iis said to be pseudo weakly clean inIifx=e+p+erxorx=-e+q+erxfor somee∈Id(I),r∈I,p∈Q(I) andq∈Q′(I). A non-unital ringIis said to be pseudo weakly clean if all of its elements are pseudo weakly clean. Clearly, a non-unital pseudo clean ring is pseudo weakly clean.
Lemma 4(1) LetRbe a pseudo weakly clean ring. Then so iseReand (1-e)R(1-e) for anye∈Id(R).
(2) LetIbe an ideal of a non-unital ringRande∈Id(R). IfIis pseudo weakly clean theneIeis pseudo weakly clean.
Proof(1) See [2, Proposition 3.4.4].
(2) Suppose thatIis pseudo weakly clean and takea∈eIe. Sinceais pseudo weakly clean inI, it is also pseudo weakly clean inRand hence pseudo weakly clean ineRe. Thus everya∈eIeis pseudo weakly clean ineRe. Hence,eIeis pseudo weakly clean.
□
By [9, Theorem 1], we see that every regular ring is pseudo weakly clean. The following theorem extends this result as following.
Theorem 7LetIbe a proper ideal of a non-unital ringR. IfIis pseudo weakly clean,R/Iis regular and idempotents lift moduloI. ThenRis pseudo weakly clean.
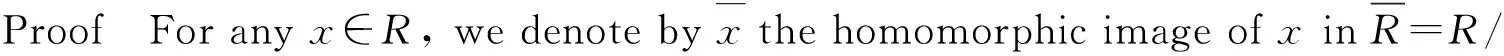
eabe=g+u1+gx(eabe-e)
eabe=-g+u2+gx(eabe-e)
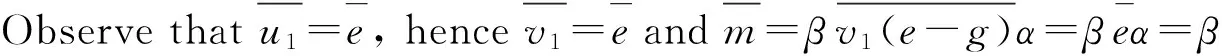
□
A ringRisπ-regular if for eacha∈Rthere exists anx∈Rand a positive integernsuch thatan=anxan. Clearly, every regular ring isπ-regular, but the converse is not true. We do not know if regularity in Theorem 7 can be weaken to the caseπ-regular or even artinian. However, we do have the following.
Lemma 5IfRis any ring andIan ideal ofRsuch thatIisπ-regular then idempotents lift moduloI.
Theorem 8LetIbe an ideal of a ringRsuch thatIandR/Iare bothπ-regular rings. ThenRis pseudo weakly clean.
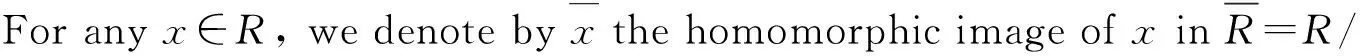
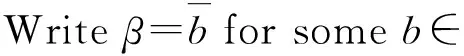
eanbe=g+u1+gx(eanbe-e)
eanbe=-g+u2+gx(eanbe-e)
Letv1,v2respectively denote the inverse ofu1,u2ineRe, andh=e-g. Multiplying the above formula byv1hand the following formula byv2hfrom the left, we havev1hanbe=v1hu1andv2hanbe=v2hu2.It follows that (bv1han)2=bv1hu1v1han=bv1han, (bv2han)2=bv2hu2v2han=bv2han, and hencem=bv1han,n=bv2hanare idempotents inRa. And (1-m)an(1-m) is pseudo weakly clean in (1-m)R(1-m). Furthermore, by the note following Lemma 4 (1) it suffices to prove that (1-m)I(1-m) is pseudo weakly clean inR. Similarly, (1-n)a(1-n) is also pseudo weakly clean inR.
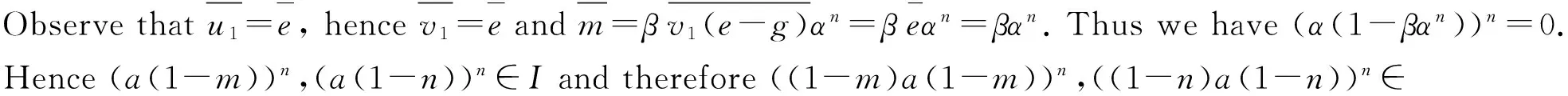
Proposition 4LetRbe a ring. IfR/J(R) is pseudo weakly clean and idempotents lift moduloJ(R), thenRis pseudo weakly clean.
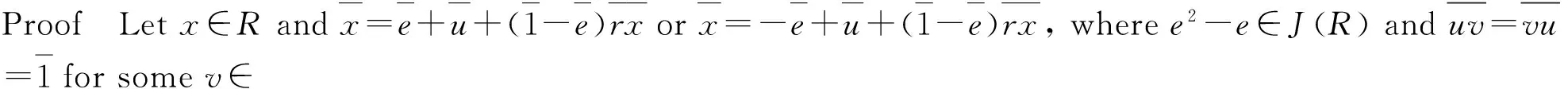
[1] STER J. Corner rings of a clean ring need not be clean[J]. Comm Algebra,2012,40(5):1595-1604.
[2] QUA K T. Weakly clean and related rings[D]. Malaya: The University of Malaya Kuala Lumpur,2015.
[3] ZHANG W R. On the ring of skew Hurwitz series[J]. Journal of North west Normal University,2006,42(42):5-8.
[4] KEIGHER W F. Adjunctions and comonads in differential algebra[J]. Pacific Journal of Mathematics,1975,59(1):99-112.
[5] WEI J. Weakly-abel rings and weakly exchange rings[J]. Acta Math Hungar,2012,137(4):254-262.
[6] WEI J C, LI L B. Quasi-normal rings[J]. Comm Algebra,2010,38(5):1855-1868.
[7] WEI J C, LI L B. Weakly normal rings[J]. Turk,2012,36(1):47-57.
[8] STER J. Weakly clean rings[J]. Comm Algebra,2014,401(401):1-12.
[9] CAMILLO V P, KHURANA D. A characterization of unit regular rings[J]. Comm Algebra,2001,29(5):2293-2295.
10.3969/j.issn.1674-232X.2016.05.012
关于Pseudo Weakly Clean环
郝亚璞,陈焕艮
(杭州师范大学理学院,浙江 杭州310036)
一个环R叫做pseudo weakly clean 环,如果R中的每一个元素都可以写成x=e+u+(1-e)rx或x=-e+u+(1-e)rx的形式,其中e是幂等元,u是可逆元.R的pseudo weakly clean性在斜幂级数环R[[x;σ]],Hurwitz级数环H(R),T(R,σ)上都满足.同时上三角矩阵的pseudo weak cleanness 得以讨论.更进一步我们证明以下几点是等价的:R是pseudo weakly clean 环;存在整数n,使得R[x]/(xn) 是pseudo weakly clean 环;存在整数n,使R[[x]]/(xn) 是pseudo weakly clean 环.
pseudo weakly clean 环;斜幂级数环;Hurwitz级数环;Weakly exchange 环;理想
date:2016-02-06
Supported by the Natural Science Foundation of Zhejiang Province (LY13A010019).
CHEN Huanyin(1963—), Male, Professor, Ph. Doctor, majored in algebra of basic mathematics.E-mail:huanyinchen@aliyun.com
O153.3MSC2010:15B99;16U99;16S70Article character: A
