一类对偶平坦球对称Finsler度量的构造

李璐璐, 宋卫东

(安徽师范大学数学计算机科学学院，安徽 芜湖 241000)



一类对偶平坦球对称Finsler度量的构造

李璐璐, 宋卫东

(安徽师范大学数学计算机科学学院，安徽 芜湖 241000)

研究对偶平坦球对称Finsler度量,通过构造对偶平坦方程的解,获得了一类对偶平坦的球对称Finsler度量.

局部对偶平坦；球对称；Finsler度量

1　引言与预备知识

对偶平坦的流形是微分几何中一类重要的研究对象,应用非常广泛.在信息几何、相对论、超弦理论中有重要的应用[1-2].沈忠民[2]曾经从Finsler几何的角度研究信息几何, 发现对偶平坦的Finsler度量在研究信息几何中有着重要的作用.在文献[3] 中将没有二次型限制的对偶平坦的概念应用到Finsler度量中.近些年来, 对偶平坦球对称Finsler度量引起了很多人的注意,文献[3-5] 中构造了大量的对偶平坦球对称Finsler度量.

开区间U⊆Rn上的Finsler度量F=F(x,y)称为对偶平坦，如果F满足下列的PDE:

[F2]xiyjyi=2[F2]xj.

(1)

第一个非黎曼的对偶平坦的Finsler度量是单位球Bn(1)⊆Rn上的Funk度量

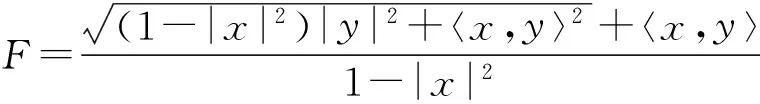
构造非黎曼的对偶平坦的Finsler度量成为Finsler几何研究的一个重要问题.最近莫小欢等[6-8]构造了一系列对偶平坦的球对称Finsler度量. 所谓球对称Finsler度量F=F(x,y),如果F满足

F(Ax,Ay)=F(x,y).

(2)

其中A是正交矩阵.这些度量最早是由S.Rutz[9]提出.

命题1[6]设F是Bn(r)⊆Rn上的Finsler度量,则F是球对称Finsler度量当且仅当存在光滑函数φ:[0,r)×R→R使得

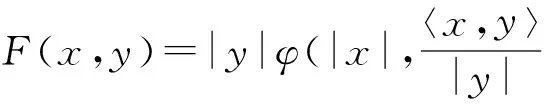
(3)

式(3)也可表示为下列形式[6]

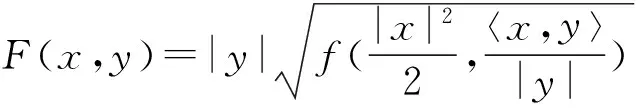
(4)

命题2[6]球对称Finsler度量(4)是对偶平坦方程(1)的解,当且仅当f满足下列的PDE:

sfts+fss-2ft=0,

(5)

本文通过构造式(5)的解获得如下结果.

定理1函数f(t,s)定义为

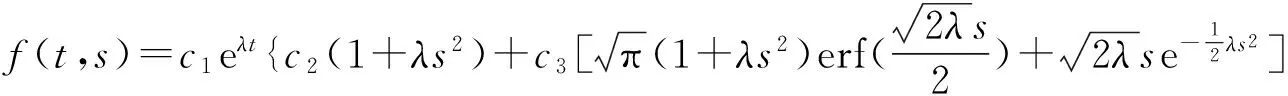
(6)

该函数是出现在概率论、统计学[10]和部分微分方程中的一种特殊函数.

定理2函数f(t,s)定义为

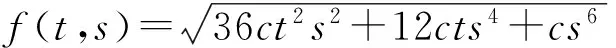
(7)

2　PDE的解

在本节构造下列PDE:sfts+fss-2ft=0的解,这个方程类似于著名的动力学中的Tricomi方程[11].

形式1设f(t,s)=φ(t)ψ(s)是式(5)的解,则满足sfts+fss-2ft=0,进而

sφ′(t)ψ′(s)+φ(t)ψ″(s)-2φ′(t)ψ(s)=0.

(8)

于是

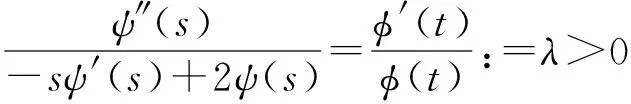
(9)

由式(9)可得

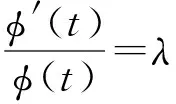
(10)

和

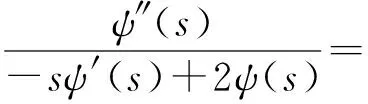
(11)

式(10)的通解为

φ(t)=ceλt.

(12)

方程(11)解得

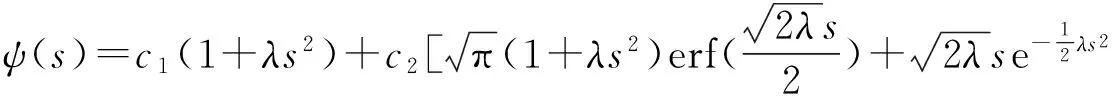
(13)

根据式(12)和式(13)得

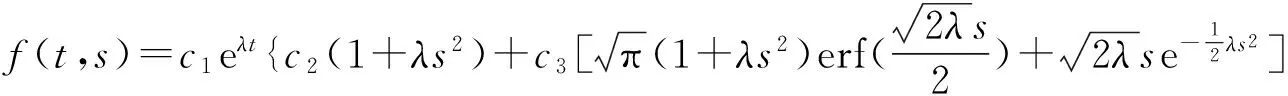
(14)

其中c1,c2,c3均为常数.

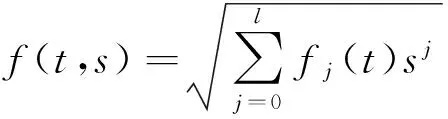
(15)

根据式(5)和式(15)得到

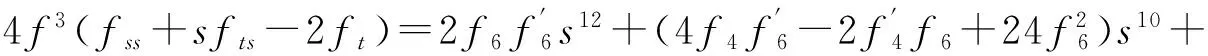
这是关于s偶次幂的多项式,因而

(16)

由此可得f2=36ct2,f4=12ct,f6=c,其中c为常数.因此式(5)的解为

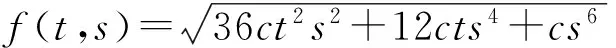
(17)

3　定理的证明

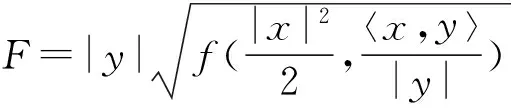
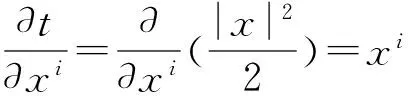
(18)

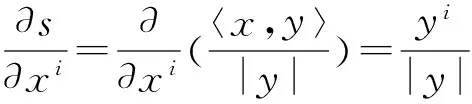
(19)

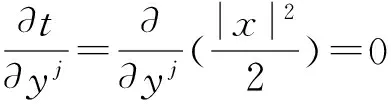
(20)

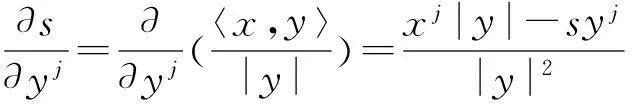
(21)

因此由式(18)-(21)得

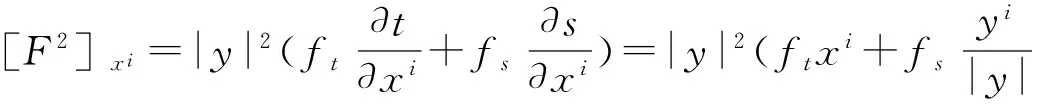
(22)

进而

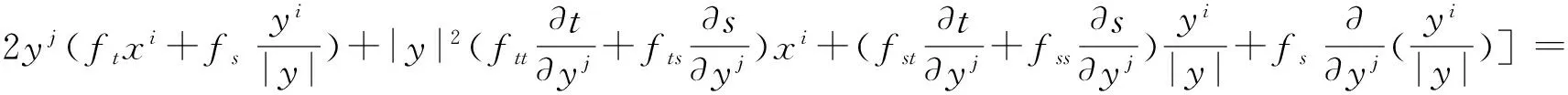
(23)

所以

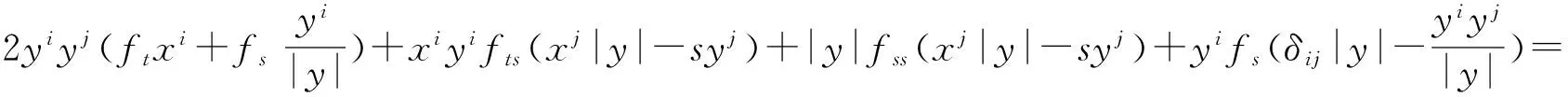
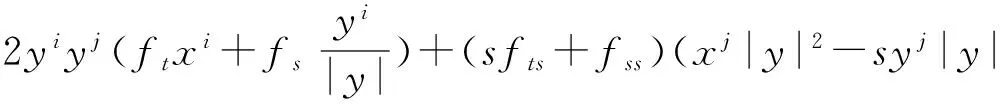
(24)

又因为sfts+fss-2ft=0,则

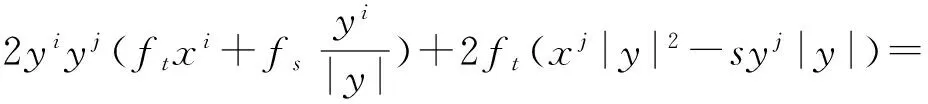
2〈x,y〉yjft+2fsyj|y|+2ftxj|y|2-2sftyj|y|.

(25)

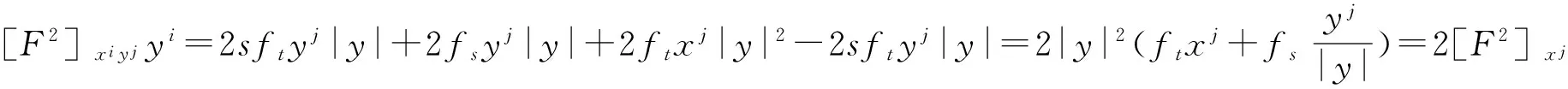
(26)

则满足对偶平坦方程(1)，即定理1得证.

定理2的证明完全类似于定理1的证明.

[1] AMARI S, NAGAOKA H. Methods of Information Geometry[M]. New York : American Mathematical Society,Oxford University Press,2000:206.

[2] SHEN Z. Riemann-Finsler geometry with applications to information geometry[J]. Chinese Annals of Mathematics, Series B,2006,27(1):73-94.

[3] MO X, ZHOU L. The curvatures of spherically symmetric Finsler metrics inRn[J].Journal of Urban Planning & Development,2012,139(2):94-103.

[4] MO X, ZHU H. On a class of projectively flat Finsler metrics of negative constant flag curvature[J]. International Journal of Mathematics,2012,23(8):84-85.

[5] ZHOU L. Projective spherically symmetric Finsler metrics with constant flag curvature inRn[J]. Geometriae Dedicata,2012,158(1):353-364.

[6] HUANG L, MO X. On some explicit constructions of dually flat Finsler metrics[J]. Journal of Mathematical Analysis and Applications,2013,405(2):565-573.

[7] LI B. On dually flat Finsler metrics[J]. Differential Geometry and its Applications,2013,31(6):718-724.

[8] CHENG X, SHEN Z, ZHOU Y. On locally dually flat Finsler metrics[J]. International Journal of Mathematics,2010,21(11):1531-1543.

[9] RUTZ S. Symmetry in Finsler spaces[J]. Contem Math,1996,196:289-300.

[10] ALZER H. Error function inequalities[J]. Advances in Computational Mathematics,2010,33(3):349-379.

[11] KÖNIGL A. Relativistic gasdynamics in two dimensions[J]. Physics of Fluids,2008,23(6):1083-1090.

[12] YU C, ZHU H. On a new class of Finsler metrics[J]. Differential Geometry and Its Applications,2011,29(2):244-254.

On the Construction of One-class Dually Flat Spherically Symmetric Finsler Metrics

LI Lulu, SONG Weidong

(College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000, China)

This paper studied the dually flat spherically symmetric Finsler metrics, and obtained one-class dually flat spherically symmetric Finsler metrics by constructing the solutions of dually flat equations.

locally dually flat; spherically symmetric; Finsler metric

2015-11-24

国家自然科学基金项目(11671005).

宋卫东 (1958—), 男, 教授,主要从事微分几何研究. E-mail：swd56@sina.com

10.3969/j.issn.1674-232X.2016.05.013

O186.12MSC2000:53B40；53C20

A

1674-232X(2016)05-0522-04