基于实时检测的扰码重建算法

马 钰 张立民



基于实时检测的扰码重建算法

马 钰 张立民*

(海军航空工程学院 烟台 264001)

基于Walsh-Hadamard变换的扰码重建算法在最大成立数准则下寻找全局最优解，是求解线性反馈关系的一种有效方法，但其计算复杂度随着变换阶数的增加而迅速增加。为降低算法的计算复杂度，论文提出一种基于实时检测的扰码重建算法，即在进行Walsh-Hadamard变换的过程中，实时判断检测对象是否为反馈关系；当检测到反馈关系时，即可停止运算。引入实时检测后可使计算复杂度平均减少50%。

线性反馈移位寄存器；扰码；反馈多项式；Walsh-Hadamard变换

1 引言

在合作通信中，通信双方预先知道调试样式及参数、编码方式及参数和通信协议等信息，接收方可以根据这些先验信息获得发送方的信源信息。在非合作通信侦察领域，被侦察方的通信参数是很难预先获得的，通常需要采用非合作的信号处理技术进行识别和估计。非合作通信信号处理按照处理对象的不同可分为3个层级：波形级、比特流级和更高等级。波形级，主要包括调制样式识别、调制参数估计、扩频码估计等；比特流级，主要包括BCH码识别、卷积码识别、交织识别、扰码识别等；更高等级，主要包括协议分析、信息恢复等[8]。本文的主要研究方向是，扰码识别算法。

扰码器作为物理层中一项重要的组成模块，被广泛应用在数字通信当中。通常可将扰码器可分为两种类型：同步扰码器和自同步扰码器，其对信息流的加扰方式稍有区别，但是它们构造的核心均在于线性反馈移位寄存器(Linear Feedback Shift Register, LFSR)的反馈关系。本文以同步扰码为例进行扰码重建算法研究，其主要包括反馈多项式检测和初始状态恢复两个方面，使用快速相关攻击算法可进行初始状态的恢复，所以主要讨论反馈多项式检测。

文献[13]在研究“利用Walsh函数解二元域方程组”的问题时首先指出，作为求解m序列极小多项式的一种有效算法，可以利用Walsh-Hadamard变换进行扰码反馈关系的检测，变换后谱系数可表示为方程组成立个数与不成立个数之差。文献[14]在游凌Walsh-Hadamard变换应用研究的基础上，进一步研究了含错扰码序列的重建问题，构建了含错情况下的扰码序列生成多项式估计算法，但在建立数学模型模中同样未考虑信息序列的影响；文献[15]基于信源不平衡性；对符合抽头位置的比特状态不平衡性进行了理论分析，提出了一种自同步扰码生成多项式的盲识别算法；文献[16]基于游程统计估计了自同步扰码的多项式阶数。另外，采用低重量倍式搜索，文献[17]中提出了检测信息序列有偏性的扰码重建算法(Cluzeau算法)，文献[15]中的算法可以归为此类统计检测算法，文献[18]通过更精确的方差估计改进了Cluzeau算法的性能，并提出了有含噪情况下的重建算法。

基于Walsh-Hadamard变换的扰码重建算法，是在全局寻找最优解，可描述为在最大成立数准则下的最优判决。以加法运算为单位进行统计，基于Walsh-Hadamard变换的扰码重建算法的计算复杂度可以表示为(22(L+1))，使用快速变换算法时可降为[19]

如果难以在可以接收的时间内检测到反馈多项式，那么将导致基于Walsh-Hadamard变换的扰码重建算法不可用。本文将Cluzeau算法中的判决过程引入到Walsh-Hadamard变换，即对每次运算进行实时检测，以判断是否为反馈关系，并计算误判概率。当检测到反馈关系时，即完成反馈关系重建，从而避免全局搜索，降低Walsh-Hadamard变换方法的复杂度。

本文首先建立扰码重建的数学模型；其次，简要介绍基于Hadamard变换的扰码重建算法；再次，给出基于实时检测的线性扰码重建算法；最后，讨论算法的计算复杂度。

2 数学模型

扰码器将伪随机序列和输入信息序列组合，输出加扰序列。通常采用LFSR产生伪随机的扰码序列，而一个LFSR序列由反馈多项式和初始状态决定。将扰码序列{s}与信息序列{x}进行模-2加，输出加扰序列{y}(图1，图2)，可表示为

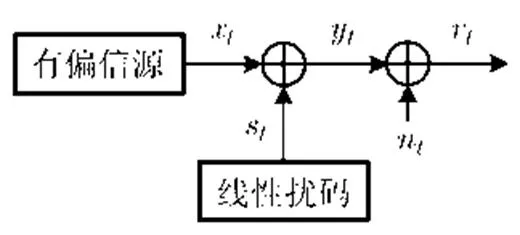
图1 信源加扰后传输框图

其中，Å表示模-2加运算。令表示LFSR中寄存器的数量，LFSR的反馈多项式表示为()。令

那么，由LFSR生成的伪随机序列满足如式(4)关系：

假设二进制信息序列{x}由一有偏信源产生，

其中，xÎ{0,1},表征有偏性。信道采用二进制对称信道模型，信道噪声n满足

本文研究扰码重建算法时，首先考虑无噪声情况，然后将算法扩展到有噪环境。

3 基于Walsh-Hadamard变换的反馈多项式估计算法

根据Walsh-Hadamard变换解含错方程组的原理，可通过变换求解m序列极小多项式，变换后谱系数的物理意义可表示为使反馈关系成立的数据量与不成立数据量之差[13]。最终，将使反馈关系成立数据量最多的多项式，作为LFSR反馈关系的估计值。下面简要回顾基于Walsh-Hadamard变换的反馈关系估计方法。

定义Walsh-Hadamard矩阵,为

其中，初始矩阵

2维列矢量，经Walsh-Hadamard变换后，生成2列矢量，可描述为

基于Walsh-Hadamard变换的反馈关系估计算法步骤如下：

(1)接收二进制序列{r}，以+1个数据为一组，进行连续分组并转换为十进制数，即把转换成十进制数，个接收数据产生个十进制数；

(3)由式(9)，进行Walsh-Hadamard变换生成2+1维矢量；

(4)将矢量中最大元素所在位置进行二进制表示，并转换为反馈关系，矢量中的第个元素所在位置的十进制表示为。

由Walsh-Hadamard变换的物理意义，将查找最大元素的估计准则称为最大成立数准则。本文中，假设线性反馈多项式的阶数已知。

4 基于实时检测的线性扰码重建算法

从上节分析可知，基于Walsh-Hadamard变换的反馈关系估计算法，是在测试集合中以最大成立数为准则寻找最优解，需要遍历每一个测试对象，在未完成Walsh-Hadamard变换之前不能得出反馈关系的估计。根据式(1)，在低阶数Walsh-Hadamard变换情况下，计算复杂度问题并不明显，但随着阶数的不断增加，Walsh-Hadamard变换的计算复杂度将呈指数增加。因此，为降低算法计算复杂度，考虑引入实时检测，即在进行Walsh-Hadamard变换的过程中不断进行反馈关系判定，当判决通过时，即完成反馈关系的估计。基于实时检测的重建算法，不需要等到变换完成后在全局寻找最优解，因此可降低算法计算复杂度。

我们国家在国际分工当中的地位要取决于出口产品的质量以及数量，我们长期占有的是数量的优势，其质量要依靠的是企业生产环节带来的附加价值，所以国际分工的档次位置是根据所创造出的附加值来区分和比较。纺织品、服装等传统生产方式仍然处于简单加工的环节，因此带来的附加值比较少。我们现阶段实现的是从中低端产品向高端工业制品的转换，附加值要在高精尖技术行业当中去实现，很多创新要不断升级改造，适应社会经济的变化，不断升级的国际分工当中，各环节的附加值仍然需要一定的时间去体现。

本节首先给出判决多项式是否为反馈多项式的方法，然后给出基于实时检测的扰码重建算法。

因为y=xÅs,，所以

{x}是有偏信息序列，所以

其中，“奇数”表示累加中的取值为奇数。根据文献[17]中定理1和文献[18]中第IV节中的方差分析可知，如果()是扰码的反馈多项式，那么当时，

渐进服从标准正态分布律。

当()不是反馈多项式时，由伪随机序列的随机性可得Pr{z=0}=0.5，那么渐进服从方差为的正态分布，其均值随()变化。在非反馈多项式情况下，均值的浮动会降低反馈多项式检测的性能，因此，令均值为，这将使得大部分(99.7%)测试值在此范围内[20]。在判决反馈多项式时，基于以下两个假设：

H0:~(,)。(()不是反馈多项式)；

Pr(=|H0)=Pr(=|H1) (16)

即

因此，可得门限

其中

虚警概率P和漏检概率P分别为

实际中，需要首先确定虚警概率指标P，然后计算达到性能条件时的门限。由式(21)得，

令

那么，判决门限满足

如果<，接受H0假设；否则，接受H1假设。

基于实时检测的扰码重建算法步骤如下：

(1)确定虚警概率P；

(2)接收二进制序列{r}，以+1个数据为一组，进行连续分组并转换为十进制数，即把rr+1r+L转换成十进制数，个接收数据产生个十进制数；

(4)根据式(25)，计算判决门限；

(5)由式(9)，设

(6)依次从1变换到2+1；

(7)计算b=aT；

(8)如果b>，那么将进行二进制表示，并转换为反馈关系；否则重复步骤(6)至步骤(8)。

值得注意的是，步骤(7)中并未考虑快速算法，同样可以使用快速算法计算b。

5 有噪条件下的扰码重建

在上节的算法分析中，并没有考虑噪声干扰的情况，本节将扩展所提算法到有噪情况。在经过二进制对称信道后，接收序列{r}可表示为r=yÅn(图1)。由y=xÅs得

r=xÅsÅn=xÅnÅs=Ås(27)

不论实时检测，还是全局查找最大成立数，算法的检测性能均与待检测数据源的有偏性息息相关。将修正后的有偏性代入式(11)和式(12)，可得到修正的H1假设：

H1:~(|μ|,σ2)

其中，

对于观测者而言，需要在一定的性能指标下，确定所需的接收数据量N。设待检测的多项式重量为，需要达到的虚警概率和漏报概率分别为P和P，令

根据式(24)，式(29)，式(30)和式(31)可得，数据量需求N满足

在重量增加的情况下，为达到既定的检测性能指标，需要更多观测数据(图3)。对于Walsh- Hadamard变换而言，待测试多项式的重量是波动变化的，在观测数据量一定的情况下检测性能会随

重量产生波动。但是，对于不满足反馈关系的高重量待检测多项式，根据式(21)可知，虚警概率指标与待检测多项式的重量无关，只决定于数据量N。因此，在考虑数据量需求时，只需关注反馈关系式的重量。从上述分析亦可知，实时检测算法的性能与数据量、数据有偏性和反馈多项式重量密切相关；同时，扰码的初始状态和反馈多项式重量分布，这些随机因素在大样本的情况下，对于统计结果的影响可以忽略。

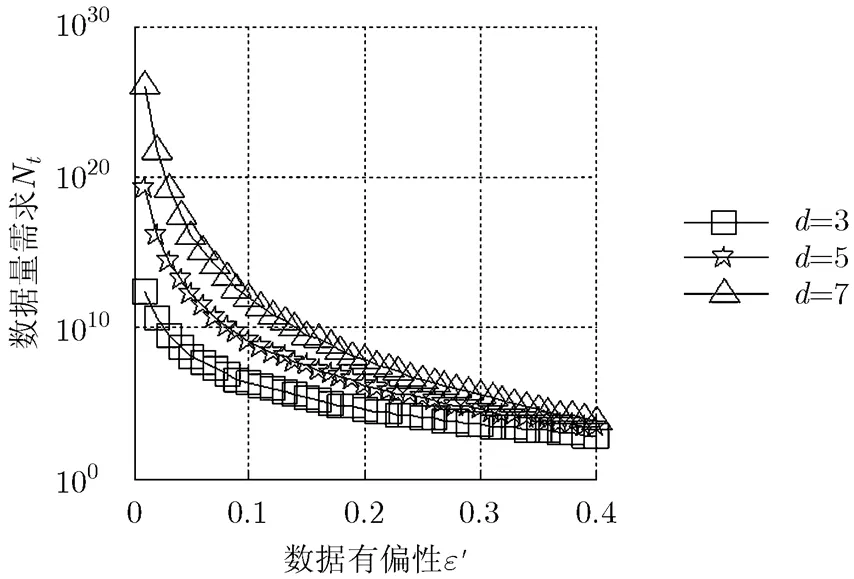
图3 不同反馈多项式重量情况下数据量需求随数据有偏性的变化曲线，Pn=Pf =105

6 计算复杂度和仿真分析

以加法运算为单位进行统计，2+1阶Walsh- Hadamard变换的计算复杂度为(22(L+1))，使用快速算法的情况下复杂度可降为[19]

在分析Walsh-Hadamard变换复杂度中，未考虑构造2(L+1)维矢量的计算复杂度，通常应用中，数据量应当在可承受的范围内，所以忽略此处的复杂度。在数据量一定的情况下，根据虚警概率指标，就可计算得到判决门限。假设扰码的反馈关系落在2(L+1)维矢量中任意位置的概率相同，那么平均进行

次判决就可得到反馈关系。根据式(34)可知，基于实时检测可以平均减少50%的运算量。

表1 基于实时检测的扰码重建算法仿真结果

图4 扰码反馈多项式为1+x2+x3+x4+x8情况下的Walsh-Hadamard变换谱系数

图5 扰码反馈多项式为1+x+x6+x7+x9情况下的Walsh-Hadamard变换谱系数

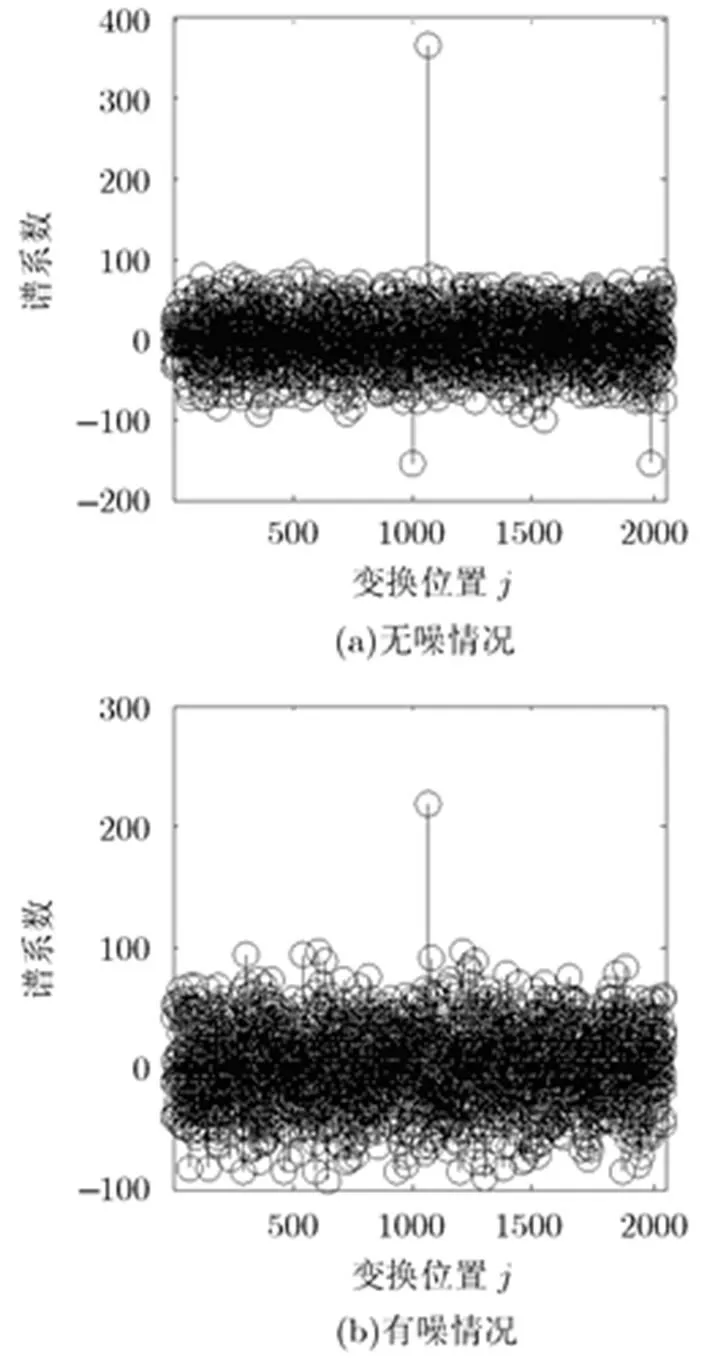
图6 扰码反馈多项式为1+x+x5+x10情况下的Walsh-Hadamard变换谱系数

7 结束语

为降低基于Walsh-Hadamard变换的扰码重建算法的计算复杂度，本文提出了一种基于实时检测的扰码重建算法，即在Walsh-Hadamard变换过程中实时对反馈关系作出判断，而不是在全局寻找最优解，进而降低了算法计算复杂度。其检测性能受稳定性因素和随机性因素两个方面影响，其中稳定性影响因素主要包括：信源有偏性、接收数据序列长度和反馈多项式重量；随机性影响因素主要包括：LFSR初始状态和反馈多项式的重量分布。这些因素同样会影响基于Walsh-Hadamard变换的扰码重建算法的检测性能，虽然在最大成立数准则下寻找全局最优解，可以平衡一些不确定因素的影响，但文中检测性能的分析亦可用来指导基于Walsh- Hadamard变换的扰码重建算法的应用。

[1] 钱国兵, 李立萍, 郭亨艺. 多入单出正交空时分组码系统的调制识别[J]. 电子与信息学报, 2015, 37(4): 863-867. doi: 10.11999/JEIT140644.

QIAN Guobing, LI Liping, and GUO Hengyi. Modulation identification for orthogonal space-time block code in multiple input single output systems[J].&, 2015, 37(4): 863-867. doi: 10.11999/JEIT140644.

[2] 沈斌, 王建新. 基于奇异值分解的直扩信号伪码序列及信息序列盲估计方法[J]. 电子与信息学报, 2014, 36(9): 2098-2103. doi: 10.3724/SP.J.1146.2013.01692.

SHEN Bin and WANG Jianxin. Blind estimation of the PN sequence and information sequence of a DSSS signal based on SVD[J].&, 2014, 36(9): 2098-2103. doi: 10.3724/SP.J.1146.2013.01692.

[3] 沈斌, 王建新. 窄带干扰条件下含有未知载频的直扩信号的伪码序列估计[J]. 电子与信息学报, 2015, 37(7): 1556-1561. doi: 10.11999/JEIT141322.

SHEN Bin and WANG Jianxin. Estimation of PN sequence in DSSS signals with unknown carrier frequency under narrow band interference[J].&, 2015, 37(7): 1556-1561. doi: 10.11999/JEIT141322.

[4] 阔永红, 曾伟涛, 陈健. 基于概率逼近的本原BCH码编码参数的盲识别方法[J]. 电子与信息学报, 2014, 36(2): 332-339. doi: 10.3724/SP.J.1146.2013.00584.

KUO Yonghong, ZENG Weitao, and CHEN Jian. Blind identi6cation of primitive BCH codes parameters based on probability approximation[J].&, 2014, 36(2): 332-339. doi: 10.3724/ SP.J.1146.2013.00584.

[5] 解辉, 王丰华, 黄知涛. 基于最大似然检测的(,1,)卷积码盲识别方法[J]. 电子与信息学报, 2013, 35(7): 1671-1676. doi: 10.3724/SP.J.1146.2012.01578.

XIE Hui, WANG Fenghua, and HUANG Zhitao. Blind recognition of (,1,) convolutional code based on maximum likelihood detection[J].&, 2013, 35(7): 1671-1676. doi: 10.3724/SP.J.1146. 2012.01578.

[6] 解辉, 王丰华, 黄知涛. 卷积交织器盲识别方法[J]. 电子与信息学报, 2013, 35(8): 1952-1957. doi: 10.3724/SP.J.1146.2013. 00287.

XIE Hui, WANG Fenghua, and HUANG Zhitao. A method for blind recognition of convolutional interleave[J].&, 2013, 35(8): 1952-1957. doi: 10.3724/SP.J.1146.2013.00287.

[7] 赵知劲, 顾骁炜, 沈雷. 非周期长码直扩信号的长扰码识别[J]. 电子与信息学报, 2014, 36(8): 1792-1797. doi: 10.3724/ SP.J.1146.2013.01454.

ZHUAO Zhijin, GU Xiaowei, and SHEN Lei. An identification method of long pseudo-random code sequence in non-periodic direct sequence spread spectral signals[J].&, 2014, 36(8): 1792-1797. doi: 10.3724/SP.J.1146.2013.01454.

[8] 高逸龙. 基于网络层的链路层协议盲分析[D]. [硕士论文], 电子科技大学, 2013.

GAO Yilong. Blind analysis of the link layer protocol based on the network layer[D]. [Master dissertation], University of Electronic Science and Technology of China, 2013.

[9] MEIER W and STAFFELBACH O. Fast correlation attack on stream ciphers[C]. Advances in Cryptology, Davos, Switzerland, 1988: 301-314. doi: 10.1007/3-540-45961-8_28.

[10] MEIER W and STAFFELBACH O. Fast correlation attack on stream ciphers[J]., 1989, 1(3): 159-176. doi: 10.1007/BF02252874.

[11] JOHANSSON T and JÖNSSON F. Improved fast correlation attacks on stream ciphers via convolutional codes[C]. Advances in cryptology, Prague, Czech Republic, 1999: 347-362. doi: 10.1007/3-540-48910-X_24.

[12] JOHANSSON T and JÖNSSON F. Fast correlation attacks through reconstruction of linear polynomials[C]. 20th Annual International Cryptology Conference Santa Barbara, California, USA, 2000: 300-315. doi: 10.1007/3-540-44598- 6_19.

[13] 游凌, 朱中梁. Walsh函数在解二元域方程组上的应用[J]. 信号处理, 2000, 16(增刊): 27-30.

YOU Ling and ZHU Zhongliang. The application of Walsh function in resolving of F(2) equations[J]., 2000, 16(Supplement): 27-30.

[14] 伍文君, 黄芝平, 唐贵林, 等. 含错扰码序列的快速恢复[J]. 兵工学报, 2009, 30(8): 1134-1138.

WU Wenjun, HUANG Zhiping, TANG Guilin,. Fast recovery of interfered scrambling code sequence[J]., 2009, 30(8): 1134-1138.

[15] 廖红舒, 袁叶, 甘露. 自同步扰码的盲识别方法[J]. 通信学报, 2013, 34(1): 136-143. doi: 10.3969/j.issn.1000-436x.2013.01. 016.

LIAO Hongshu, YUAN Ye, and GAN Lu. Novel blind recognition method for self-synchronized scrambler[J]., 2013, 34(1): 136-143. doi: 10. 3969/j.issn.1000-436x.2013.01.016.

[16] 黄芝平, 周靖, 苏绍璟, 等. 基于游程统计的自同步扰码多项式阶数估计[J]. 电子科技大学学报, 2013, 42(4): 541-545. doi: 10.3969/j.issn.1001-0548.2013.04.002.

HUANG Zhiping, ZHOU Jing, SU Shaojing,. Order estimation of self-synchronizing scrambling polynomial based on run statistic[J].2013, 42(4): 541-545. doi: 10.3969/j.issn.1001-0548.2013.04.002.

[17] CLUZEAU M. Reconstruction of a linear scrambler[J]., 2007, 56(9): 1283-1291. doi: 10.1109/TC.2007.1055.

[18] LIU X B, KOH S N, WU X W,. Reconstruction of a linear scrambler with improved detection capability and in the presence of noise[J]., 2012, 7(1): 208-218. doi: 10.1109/ TIFS.2011.2169790.

[19] AHMED N and RAO K R. Orthogonal Transforms for Digital Signal Processing[M]. Berlin Heidelberg, Springer, 1975.

[20] MA Yu, ZHANG Limin, and WANG Haotong. Reconstructing synchronous scrambler with robust detection capability in the presence of noise[J]., 2015, 10(2): 397-408. doi: 10.1109/TIFS.2014.2378143.

Reconstruction of Scrambler with Real-time Test

MA Yu ZHANG Limin

(,264001,)

Scrambler reconstruction algorithm based on Walsh-Hadamard transformation is a promising method to recover the feedback relationships, which picks out the optimal solution under the rule of maximum number. However, its computation complexity increases markedly with the transformation degree. In order to reduce the complexity, a method to reconstruct the scrambler with real-time test is proposed. In the process of Walsh- Hadamard transformation, the objects can be tested in real time. If the feedback polynomial is detected, the transformation can be terminated. With real-time test, the computation complexity can be reduced about 50% on average.

Linear Feedback Shift Register (LFSR); Scrambler; Feedback polynomial; Walsh-Hadamard transformation

TN919

A

1009-5896(2016)07-1794-06

10.11999/JEIT151068

2015-09-21；改回日期：2016-04-08；网络出版：2016-05-24

张立民 iamzlm@163.com

泰山学者工程专项经费

Taishan Scholar Special Foundation

马 钰： 男，1986年生，助理工程师，博士生，研究方向为非合作通信信号处理.

张立民： 男，1966年生，教授，研究方向为卫星信号处理及应用.