移动混合传感网中节点自主部署算法

秦宁宁 余颖华 吴德恩



移动混合传感网中节点自主部署算法

秦宁宁*余颖华 吴德恩

(江南大学轻工过程先进控制教育部重点实验室 无锡 214122)

针对节点感知半径不均衡的移动传感网络节点的部署问题，论文提出一种基于VL (Voronoi Laguerre)图分割的节点自主部署算法(Autonomous Deployment Algorithm, ADA)。ADA先对目标区域做VL图划分，将目标区域的覆盖任务在各个传感器节点之间进行分配。分配到覆盖子区间任务的节点通过构造VL受控多边形来确定下一轮候选目标位置。未分配到覆盖子区间的节点则根据自身与邻居节点感知圆及目标区域边界的几何位置关系计算所受虚拟力，最终确定下一轮目标点坐标。网络各个节点通过逐轮更新自身位置，从而提高网络覆盖。仿真结果表明，ADA算法在网络覆盖率、节点部署速度和节点分布均匀性等方面具有明显的优势。

移动传感网络；VL (Voronoi Laguerre)图；受控多边形；覆盖率

1 引言

在移动传感器网络的现实应用中，节点的初次部署通常由随机抛撒实现，因此很难保证对检测区域的覆盖率以及网络连通性[1]，节点需要自身的再次部署定位以获得满足应用需求的感知覆盖。

针对移动节点的再次部署问题[2,3]，文献[4]提出了一种基于Voronoi多边形[5,6]形心的部署策略(Centroid-Based Scheme, CBS)，将目标区域的覆盖问题转换为每个节点对各自Voronoi多边形的覆盖优化问题。文献[7]在CBS的基础之上提出了一种基于Voronoi盲区多边形形心的部署策略，可有效提高网络覆盖率，但子区间的划分方法只适合节点感知半径均一的同构网络。针对节点感知半径不同的异构网络，文献[8]提出了一种基于VL (Voronoi Laguerre)图[9]的Minmax部署策略。该算法部署速率相对较高，但部署效果易受节点位置的影响，部署完成后存在部分小感知半径节点始终位于其他节点的感知范围内，造成覆盖冗余，鲁棒性较差。文献[10]采用 MW-Voronoi图分割目标区间，各个节点在自身所受虚拟力[11]的作用下定向移动。但由于各子区间包含曲线边界，增大了算法运算复杂度[12]。

基于上述分析，本文在文献[8]的基础之上提出了一种面向移动异构传感器网络[13]的节点自主部署算法(Autonomous Deployment Algorithm, ADA)。算法采用VL图划分目标区域，针对由此产生的两类节点分别采用不同的策略进行移动部署，不仅克服了VorLag算法鲁棒性较差的缺点，同时避免了因节点半径差异而造成的覆盖冗余，可以有效提高单个节点覆盖效率、网络覆盖率以及节点分布均衡性。

2 基本知识

2.1 网络模型

2.2 VL图

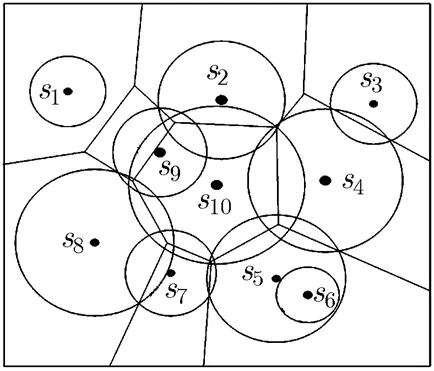
图1 VL图划分

在VL图中，VL多边形内盲区的判定可转化为对多边形顶点的点覆盖判决，具体对应关系为：如果VL多边形顶点不完全被其对应节点覆盖，则该VL多边形内存在覆盖盲区，且每个被覆盖顶点同时被另外两个一类节点覆盖；否则，该VL多边形内不存在覆盖盲区。

3 ADA算法

3.1 一类节点的VCS部署

根据节点对其VL多边形顶点的覆盖关系，节点VL受控多边形的构造情况为：若VL多边形的顶点未全部被覆盖，则可根据定义构造VL受控多边形；若VL多边形的所有顶点均被覆盖，内无覆盖盲区，VL受控多边形不存在。

3.1.1 节点候选位置

3.1.2 VL受控多边形的构造

不失一般性，以图2网络为例，介绍VL受控多边形的构造机理。图2中节点覆盖了自身VL多边形()的顶点，根据VL多边形非边界顶点的覆盖情况，此时节点和也同时覆盖。由于,对的覆盖影响，导致内由节点负责的最大净覆盖区域变小。此时按定义为构造受控多边形(，分别对,运行VCS策略，所得候选目标位置分别为图2中三角形和圆形。显然，当节点位于圆形位置时可实现对更有效的覆盖。

由VL受控多边形的定义可知，受控多边形的构造中有时也会出现凹多边形，如图3中的受控多边形。为简化VCS的计算复杂度，并兼顾邻居节点对VL多边形覆盖影响，可直接将受控多边形中内角为钝角的顶点剔除，由剩余顶点构成的多边形，即为考虑了邻居节点覆盖影响后的受控凸多边形。

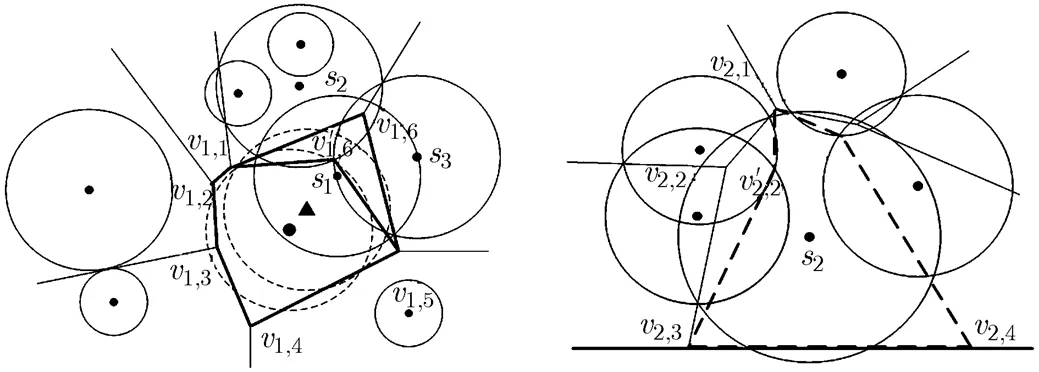
图2节点候选位置选择 图3 VL-受控凹多边形

3.2 二类节点的VRS部署策略

在节点部署过程中，文献[8]未考虑二类节点的移动需求，部署完成后存在部分二类节点位于一类节点的感知范围内，造成网络覆盖率降低以及资源浪费。为使二类节点自主远离临近节点以及检测区域边界，可为其设计如下部署策略：

3.3 ADA算法步骤

在VCS和VRS部署策略中，为减小能量损耗，当一类节点对VL多边形的覆盖面积增长率不小于门限值，二类节点所受合斥力不小于门限斥力时，节点才能移动。ADA算法实现步骤如表1所示。

表1 ADA算法

4 仿真实验

4.1 覆盖率

图4(a)–图4(c)显示了某网络单次ADA算法对60个节点的部署过程。其中，初始覆盖率为, 5次迭代后达到，经过14次迭代后覆盖率稳定在。图4(d)–图4(f)显示了简化ADA算法的节点部署情况。在相同初始条件下，经过16次迭代，简化ADA算法可取得的最终覆盖率约为。虽然简化ADA的覆盖性能略低于ADA，但由于具有更高的运算效率，增强了算法本身的现实应用性。

图4 ADA和简化ADA算法下的某次部署过程

为考察ADA的性能，在相同条件下分别运行VorLag, ADA和简化ADA算法，网络覆盖率的变化如图5所示。每次迭代中，ADA和简化ADA的覆盖率总高于VorLag。这是由于ADA通过构造受控多边形来优化节点候选目标位置，增强了节点对自身VL多边形的覆盖效果。同时二类节点自主远离邻近节点的感知区域，覆盖冗余的减小也相应提高了网络净覆盖面积。ADA中节点的候选位置为节点多边形形心和最小最大点二者中可提高更高覆盖的点，而简化ADA中节点的候选位置仅由多边形的形心决定，因此在每次迭代中，简化ADA的网络覆盖率会略低于ADA，但明显高于VorLag算法。

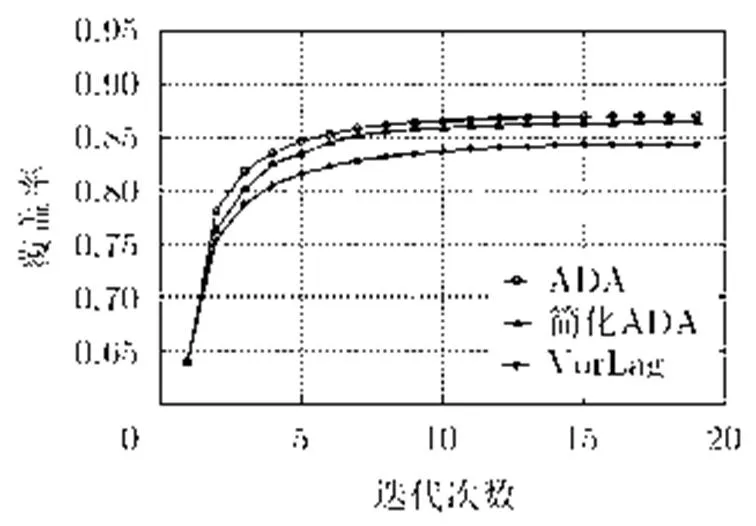
图5平均覆盖率随迭代次数的变化

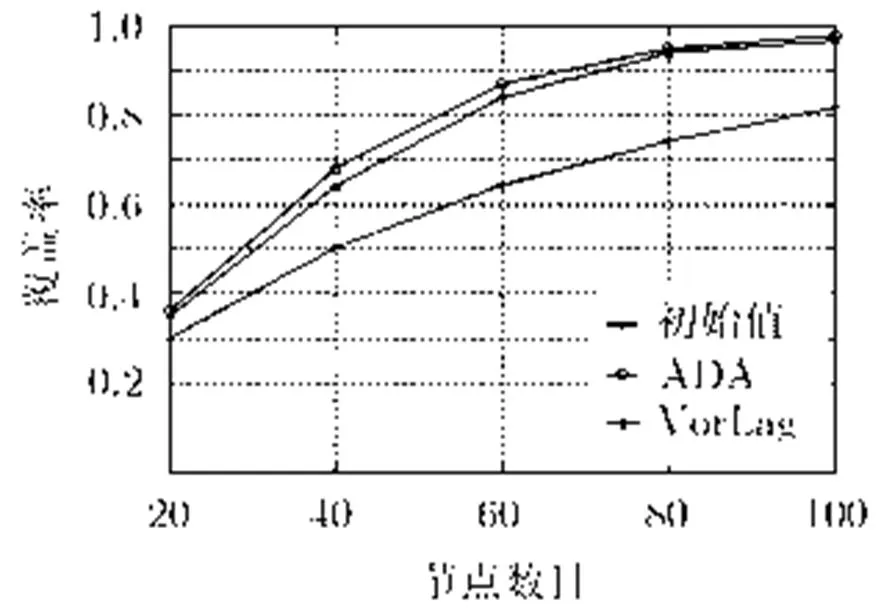
图6覆盖率随节点数目的变化

4.2 快速性

图7针对不同的节点数目，分析了VorLag和ADA算法中节点移动的平均次数。当节点数目小于60时，随着节点数目的增加，每个节点划分到的VL多边形相对变小，节点需要通过更多次移动才能实现对VL多边形的最大覆盖。当节点数目高于60以后，越来越多的节点完全覆盖自身的VL多边形，节点移动较少的次数即达到终止条件，最终导致节点移动次数随着节点数目的增加逐渐减小。

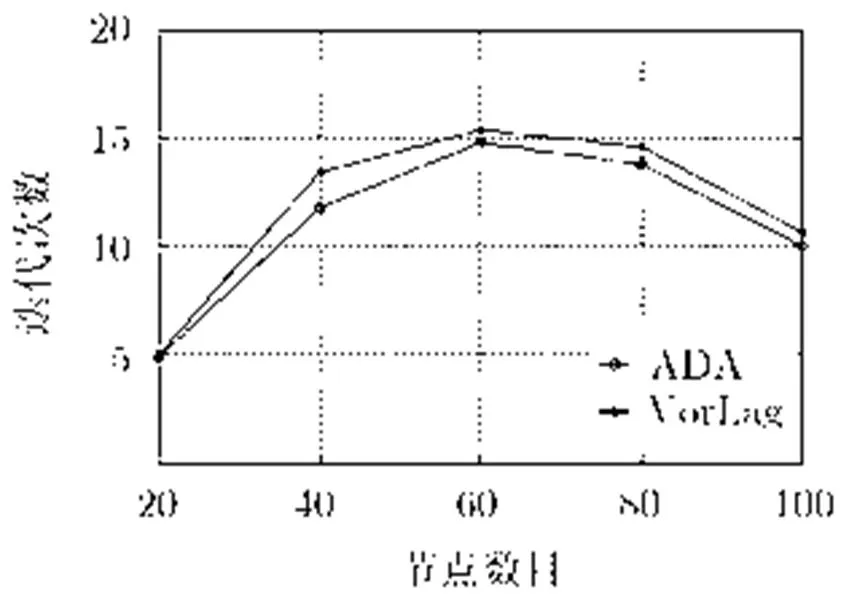
图7所需迭代次数随节点数目的变化

4.3 节点覆盖性能指标

参考文献：[15]，定义节点感知半径不均衡网络节点分布均匀性指标，即为每个节点与其一跳邻居距离与两者感知半径和差值的绝对值的标准差均值。表2统计了VorLag和ADA在不同节点数目下，覆盖效率CE以及的变化情况。由表2数据可知，在任何节点数目下，ADA算法的覆盖性能均优于VorLag算法。当较小时，网络节点分布均匀性随节点个数的增加而变好，当高于某个数值时，随节点数目的增加，节点分布均匀性逐渐变差。随着的增大，区域覆盖冗余程度变高，两种算法中的节点覆盖效率均呈下降趋势，但ADA始终优于VorLag算法。

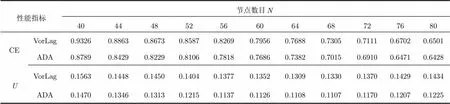
表2 节点覆盖性能指标

5 总结

本文提出了一种移动混合传感网节点的自主部署算法，针对目标区间划分产生的两类节点，分别采用不同的策略确定其候选位置。其中，一类节点通过构造VL受控多边形，将Minimax策略和CBS策略相结合来优化节点候选目标位置；二类节点根据自身与周围节点的几何位置关系计算所受虚拟斥力，从而确定移动目标点位置，在提高网络覆盖率和部署快速性的同时，增强了网络节点分布均匀性。网络中所有节点通过逐轮移动最终实现对检测区域的最大覆盖。

参 考 文 献

[1] 钱志鸿, 王义君. 面向物联网的无线传感器网络综述[J]. 电子与信息学报, 2013, 35(1): 215-227. doi: 10.3724/SP.J.1146. 2012.00876.

QIAN Zhihong and WANG Yijun. Internet of things-oriented wireless sensor networks review[J].&, 2013, 35(1): 215-227. doi: 10.3724/ SP.J.1146.2012.00876.

[2] MAHBOUBI H. Distributed deployment algorithms for efficient coverage in a network of mobile sensors with nonidentical sensing Capabilities[J]., 2014, 63(8): 3998-4016.

[3] MAHBOUBI H, MOEZZI K, AGHDAM A G,. Distributed deployment algorithms for improved coverage in a network of wireless mobile sensors[J]., 2014, 10(1): 163-174.

[4] LEE H J, KIM Y H, HAN Y H,. Centroid-based movement assisted sensor deployment schemes in wireless sensor networks[C]. the IEEE 70th Vehicular Technology Conference Fall (VTC 2009-Fall), Anchorage, 2009: 20-23.

[5] CORTES J and BULLO F. Coordination and geometric optimization via distributed dynamical systems[J]., 2005, 44(5): 1543-1574.

[6] BARTOLINI N, BONGIOVANNI G, POTTA T L,. Voronoi-based deployment of mobile sensors in the face of adversaries[C]. 2014 IEEE International Conference on Communications (ICC), Sydney, 2014: 532-537.

[7] 方伟, 宋鑫宏. 基于Voronoi图盲区的无线传感器网络覆盖控制部署策略[J]. 物理学报, 2014, 63(22): 220701.

FANG Wei and SONG Xinhong. An coverage control

deployment strategy of wireless sensor networks based on blind-zone of voronoi diagram[J]., 2014, 63(22): 220701.

[8] BARTOLINI N, CALAMONERI T, LA PORTAT T F.. Autonomous deployment of heterogeneous mobile sensors[J]., 2011, 10(6): 753-766.

[9] IMAI H, IRI M, and MUROTA K. Voronoi diagram in the laguerre geometry and its applications[J]., 1985, 14(1): 93-105.

[10] MAHBOUBI H and AGHDAM A G. Distributed deployment strategies to increase coverage in a network of wireless mobile sensors[C]. Proceedings of 2013 American Control Conference (ACC), Washington, 2013: 17-19.

[11] LIN T Y, SANTOSO H A, and WU K R. Global sensor deployment and local coverage- aware recovery schemes for smart environments[J].,2015, 14(7): 1382-1396.

[12] KASHI S S and SHARIFI M. Coverage rate calculation in wireless sensor networks[J]., 2012, 94(11): 833-856.

[13] 杜晓玉, 孙力娟, 郭剑, 等. 异构无线传感器网络覆盖优化算法[J]. 电子与信息学报, 2014, 36(3): 696-702. doi: 10.3724/ SP.J.1146.2013.00730.

DU Xiaoyu, SUN Lijuan, Guo Jian,. Coverage optimization algorithm for heterogeneous WSNs[J].&, 2014, 36(3): 696-702. doi: 10.3724/SP.J.1146.2013.00730.

[14] CORTES J, MARTINEZ S, KARATAS T,. Coverage control for mobile sensing networks[J]., 2004, 20(2): 243-255.

[15] NOJEONG H and VARSHNEY P K. An intelligent deployment and clustering algorithm for a distributed mobile sensor network[C]. 2003 IEEE International Conference on Systems, Man and Cybernetics, Washington, 2003, 5: 4576-4581.

Autonomous Deployment Algorithm in Mobile Heterogeneous Networks

QIN Ningning YU Yinghua WU De’en

(,,,214122,)

To solve the deployment problem of nodes with unbalanced sensing radiuses in mobile sensor network, an Autonomous Deployment Algorithm (ADA) based on the VL (Voronoi Laguerre) graph is proposed. First, the VL graph is used to divide the target area, the coverage tasks of target area are allocated among different sensor nodes. Then, the node assigned with coverage subinterval confirms its candidate target location in next round by structuring the VL controlled polygon. The node without sub-range calculates its virtual repulsion according to the geometrical position relationship with its neighbor nodes’ perception circles and the target area’s borders to ultimately ascertain the target point moving to. Each node in the network updates its position by rounds to improve the network coverage. The simulation results show ADA algorithm has obvious advantages in network coverage rate, deployment speed, nodes’ distribution uniformity and so on.

Mobile sensor network; VL (Voronoi Laguerre) graph; Controlled polygon; Coverage rate

TP393

A

1009-5896(2016)07-1838-05

10.11999/JEIT151063

2015-09-21；改回日期：2016-03-03；网络出版：2016-04-26

秦宁宁 ningning801108@163.com

江苏省“六大人才高峰”第十一批高层次人才项目(DZXX-026)，国家自然科学基金(61304264)，江苏省产学研联合创新资金前瞻性联合研究项目(BY2014023-31)

The Eleventh Batch High-level Talents Project of “Six Talent Peaks” in Jiangsu Province (DZXX-026), The National Natural Science Foundation of China (61304264), Union Innovation Funds Prospective Joint Research Project in Jiangsu Province (BY2014023-31)

秦宁宁： 女，1980年生，副教授，硕士生导师，主要研究方向为无线传感器网络及应用.

余颖华： 女，1989年生，硕士生，研究方向为无线传感网覆盖.

吴德恩： 男，1988年生，硕士生，研究方向为无线传感网覆盖.