基于空域稀疏性的自适应频谱检测算法
2016-10-14于宏毅胡赟鹏沈智翔
于宏毅 程 标 胡赟鹏 沈智翔
基于空域稀疏性的自适应频谱检测算法
于宏毅 程 标*胡赟鹏 沈智翔
(解放军信息工程大学信息系统工程学院 郑州 450002)
现有的频谱检测算法没有充分利用信号在角度维的稀疏性质。该文根据角度维的稀疏特性建立信号模型,通过稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)算法解决稀疏信号的重构问题,并在迭代过程中引入二元假设检验思想,推导出一种自适应门限的选取策略,把传统的重构算法转化为一个针对不同来波方向的信号检测问题。该算法能够在恒虚警概率下对多信号进行全盲检测,同时实现信号来波方向的精确估计。实验结果证明,自适应判决方法能够有效地提高稀疏重构算法的重构精度,降低运算复杂度,参数估计精度和信号检测性能相比于现有算法得到明显的提升。
频谱检测;稀疏贝叶斯学习;恒虚警概率;自适应门限
1 引言
随着电子通信设备的广泛应用,频谱资源变得愈发紧张和拥挤。特别是在复杂电磁环境下,由于环境噪声和干扰信号的存在,接收机通常会接收到多个信号资源,这些信号在时域和频域上相互重叠难以区分,给后续的参数估计和调制识别等信号分析工作带来困难。频谱检测技术能够针对一段频谱范围内的信号进行检测,感知频谱范围内的无线电资源和电磁环境变化态势,在军事和民用领域均有着非常重要的研究意义和广阔的应用前景。
传统的频谱检测算法包括能量检测法[1]、循环平稳检测法[2]和匹配滤波器检测法[3]等。传统方法通过提取信号在时间或频率等维度的信息进行频谱检测,但是存在一定的缺陷,比如能量检测法不能摆脱噪声不确定度的影响,循环平稳检测法计算量较大,匹配滤波器检测法需要已知信号或噪声功率信息等。近年来,部分学者在阵列天线的基础上,将角度维信息引入到频谱检测算法中,不仅实现了频谱的全盲检测,还提供了信号的空间方位信息,为角度维的频谱接入提供了重要参数[4]。文献[5]利用阵列天线技术,根据协方差矩阵构建检测统计量,提高了频谱检测算法的检测性能。文献[6]将非线性后置处理思想引入到空间能量谱估计中,通过判断阵列噪声频谱在频段间的幅度起伏和目标信号频谱幅度起伏的大小完成信号检测。文献[7]根据信号在空间谱上呈现出的幅度特征,提出了两种判决统计量的构造方法,并分别推导了合适的检测门限。但是上述算法只是利用空间谱的起伏特征,没有考虑到信号在角度域的稀疏特性。
对此,本文根据信号在角度域的稀疏特性构建稀疏模型,在稀疏重构算法的基础上推导频谱检测方法。稀疏重构算法作为信号处理领域的一项重要技术,在信号检测问题中得到越来越广泛地研究。文献[8]根据信道的稀疏特性,分别在已知和未知信道状态信息的条件下推导了分布式频谱检测算法。文献[9]假设信号在空间坐标上是稀疏的,利用重构结果估计地理谱特征(Geographical-Spectral Pattern, GSP),能够检测信号个数并实现目标定位。文献[10]在NeymanPearson准则下引入一种基于Lasso估计的稀疏信号检测算法,降低了运算复杂度,提高了在低信噪比条件下的检测性能。文献[11]在贝叶斯框架下求解非平稳信号的稀疏表示形式,根据系数状态序列进行信号检测和分类。文献[12]提出一类基于最大后验估计的稀疏表示算法,通过固定门限和重构系数的大小关系完成信号检测。
受上述启发,本文将SBL算法引入频谱检测问题中,利用超参数幅度值判断所有预设角度上信号是否存在。但是,现有的重构算法没有给出合理判决门限的选取策略。对此,本文在重构迭代过程中引入一种自适应判决的处理方法,能够在恒虚警概率下对重构结果中的超参数进行检测判断,实质上等效于对不同入射方向上的信号进行检测判断,较好地提高了算法的重构精度。同时由于删除了无效方向对应的基向量,算法的运算复杂度大幅降低。
2 信号模型
一个阵元数目为的阵列接收个通信信号,信号与正北方向的夹角分别为,第个信号在第个阵元上的时域波形可以表示为
为了提高重构算法的准确度,进一步建立多观测向量(Multiple Measurement Vector, MMV)模
型[14]。以相同观测时长采集段样本数据,每一段数据含有个样本点,式(3)的信号模型可以变形为式(4)的MMV模型形式:
由于信号只是从空域上的个角度入射到阵列,因此稀疏矩阵只有与实际入射角度相对应的行向量是非零的,即稀疏矩阵中非零行对应字典矩阵中的角度代表着信号的入射角度。需要指出的是,式(5)中时延差仅跟和有关,因此,在已知阵元布设位置的条件下,即使阵型不满足均匀线阵等标准结构,同样能够构造字典矩阵,说明本文算法适用于非标准结构的天线阵列。
3 稀疏重构算法
为了识别待检测频带范围内的信号分布情况,联合考虑位于频带内的个频点,推导多字典稀疏贝叶斯学习 (Multiple Dictionary SBL, MDSBL) 算法。为了简便表示,用代替,表示的第列向量。根据不同频点上信号的统计独立特性,检测频带内稀疏矩阵的似然函数可以表示为
超参数和噪声功率的计算可以转化为求解第2类似然函数问题,即求解边缘似然函数的最大似然问题。下面使用EM算法求解最大似然解。在E步骤中,将看作完备数据集,对数似然函数可以表示为
计算完备数据集似然函数的条件期望,Q函数可以分成式(10)所示的两个独立的部分:
其中,
在步骤中,令Q函数的偏导数方程等于零,根据和计算得到:
4 自适应判决门限
本节引入一种自适应判决方法依次对超参数进行检测。假设更新后的超参数和噪声功率分别为和,以第个超参数为例,规定两种假设分别为
通过式(23)发现,统计变量的概率密度函数只与已知参数有关,与信号能量和噪声功率等随机参量无关,因此算法可以在恒虚警概率的性质下完成信号检测。假设恒虚警概率检测条件下的门限为,虚警概率可以表示为
5 算法分析
经典的SBL算法[17]利用固定门限值把小于门限的超参数置为零,这种方法能够通过降低矩阵运算的维数提高运算速度,但是实际场合中无法准确地找到合理的门限值,从而影响参数估计的精度并导致算法的不稳定;在实际的参数估计问题中,学者们的通常做法是不对超参数进行置零处理,但是这种不使用门限的方法[18](None-Threshold MDSBL, NTh-MDSBL)只能得到真实结果的近似表示,在低信噪比下参数估计的精度较差,而且运算复杂度非常高。本文提出的自适应判决门限方法(Adaptive- Threshold MDSBL, ATh-MDSBL)可以较好地解决以上问题,下面逐一分析。
5.1 统计判决量分析
5.2 运算复杂度分析
对比一次循环迭代中ATh-MDSBL方法和NTh-MDSBL方法的运算复杂度。文献[18]推导NTh-MDSBL方法在一次循环迭代中的运算复杂度为。本文ATh-MDSBL方法的复杂度集中在式(16)、式(17)和式(26),假设某一次循环迭代中有效超参数的个数为,当仅考虑乘法运算的次数时,式(16)的运算复杂度为。式(17)只需求矩阵的迹,其运算复杂度为。式(26)用于对更新后的有效超参数进行自适应判决,其运算复杂度为。因此,ATh-MDSBL方法进行一次循环迭代的总运算复杂度为。由于ATh-MDSBL方法通过式(26)的自适应判决可以准确地删除无效超参数,即,使得一次循环迭代中的运算复杂度大幅地降低,较好地解决了传统NTh-MDSBL方法运算复杂度较高的问题。
6 实验仿真及分析
使用9元均匀直线阵接收2个QPSK信号,信号载波频率均为100 Hz,带宽为中心频率的40%,入射方向分别为和。接收机噪声为加性高斯白噪声,阵元间距为中心频率所对应信号波长的一半。由于最高频率是带宽的整数倍,采样频率设置为80 Hz,将空间角度区间等分为360个角度值,每次仿真的蒙特卡洛循环次数设置为1000次。
为了提高算法的稳定性,在检测判断之前需要进行初始化,本文采取的方法是根据式(16)和式(17)进行15次EM迭代处理,将计算结果作为本文算法的初始值进行检测判断。此外,当每次迭代运算后的结果趋于稳定,即满足时算法停止迭代计算,收敛门限。
首先,通过对比重构效果图验证自适应判决方法的有效性。假设信号的信噪比分别为和5 dB,虚警概率设置为,样本点总数为512点,其中每个数据段包含64个样本点。图1为算法收敛后所有超参数的幅度情况。如图1(a)所示,当信号的信噪比相差较大时,NTh-MDSBL方法由于本身运算精度的问题,会在信噪比较大的真实信号对应超参数两侧出现较为明显的干扰,而且幅度值大于信噪比较小的信号对应超参数的幅度值,此时仅根据幅度值无法区分信号和干扰。如图1(b)所示,ATh- MDSBL方法能够准确地抑制干扰的出现,重构结果与传统方法相比更为稀疏,非常接近真实信号。
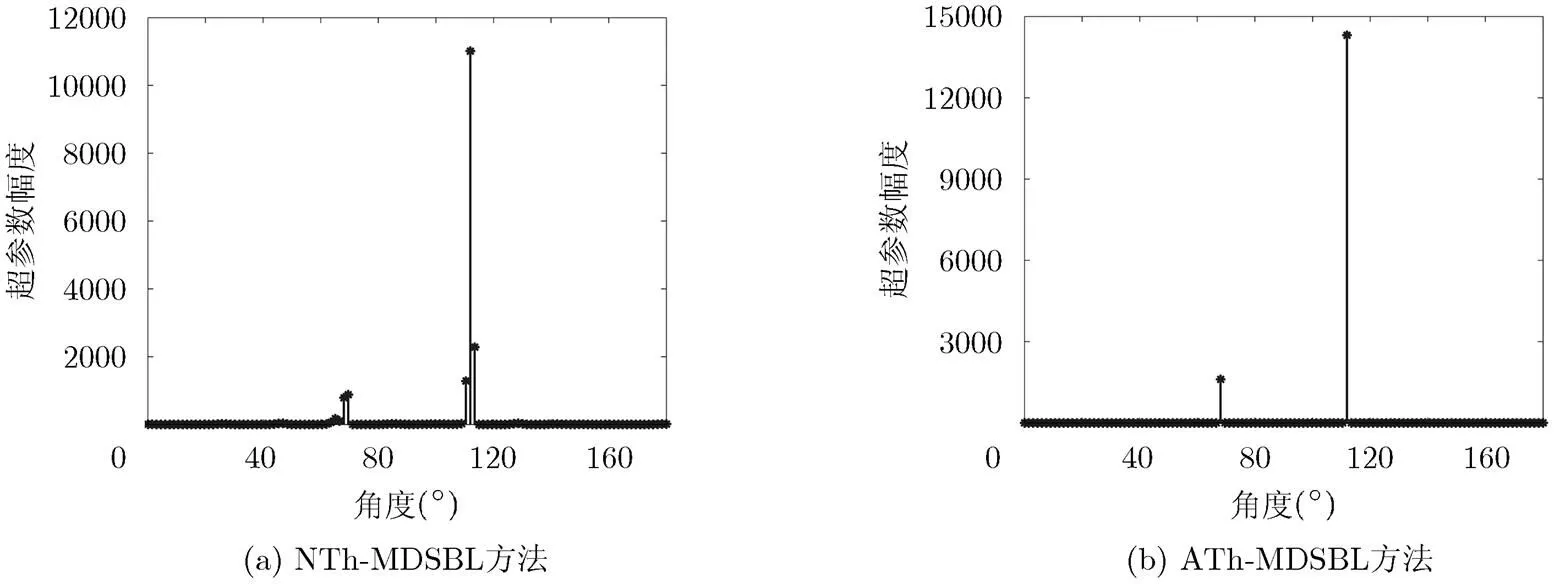
图 1 两种方法的重构效果图
为了进一步展示ATh-MDSBL方法的中间过程,图2统计了ATh-MDSBL方法在一次迭代过程中部分超参数幅度随迭代次数的变化情况。其中,信号1和信号2分别表示有效超参数的幅度,干扰1和干扰2表示大信号两侧超参数的幅度。前15步为初始化过程,通过图2可以看出在真实超参数的周围会产生较为明显的干扰。然而从第16步开始算法进入自适应判决阶段,算法根据式(26)能够准确地识别出代表实际信号来波方向的超参数,同时将无效的超参数置为零。进一步统计在第16步时超参数的判决统计量与门限的关系,在虚警概率为条件下判决门限等于1200,此时小信号的判决统计量为1965,大信号的判决统计量为2897,两个干扰的判决统计量分别为592和654,可以看出信号和干扰的判决统计量之间具有明显的区分度。
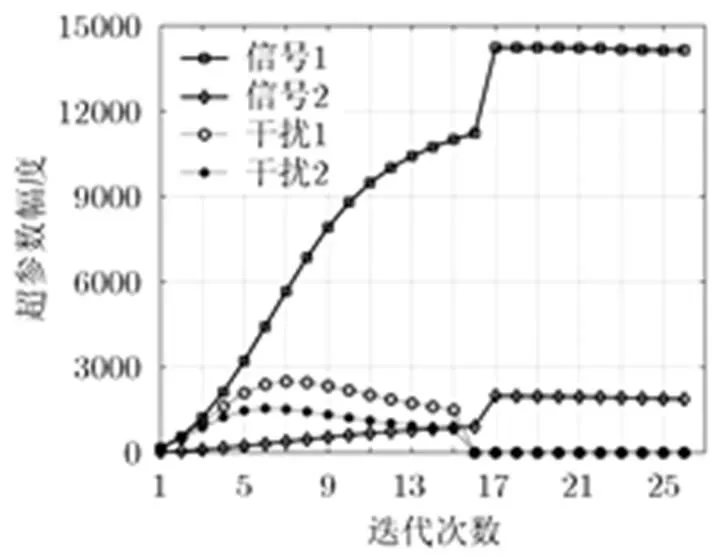
图 2 本文算法迭代过程中超参数的变化曲线
此外,通过图2可以发现ATh-MDSBL方法基本可以在30步内完成收敛,远小于NTh-MDSBL方法收敛时的迭代步数。因此,从一次循环迭代计算量和总收敛步数两个方面分析可知,ATh- MDSBL方法的总运算复杂度小于NTh-MDSBL方法,即自适应门限的引入能够有效地降低已有算法的运算复杂度。
接下来,验证本文算法与现有宽带DOA估计算法的参数估计性能。现有宽带DOA估计算法可以分为两类:(1)基于信号子空间的估计方法,包括投影子空间正交测试方法(Test of Orthogonality of Projected Subspaces, TOPS)、非相干信号子空间方法(Incoherent Signal Subspace Method, ISSM)和相干信号子空间方法(Coherent Signal Subspace Method, CSSM);(2)基于稀疏性的估计方法,包括ATh-MDSBL方法、NTh-MDSBL方法[18]和WCMSR方法[19]。以上所有算法的空间范围为到,等份成360个搜索格点,样本点总数为320点,其中每个数据段包含64个样本点,两个信号的信噪比保持相同,均从变化到21 dB,本文算法的虚警概率为1%。图3展示了DOA估计的均方根误差(Root of Mean-Square-Error, RMSE)随信噪比的变化情况。在低信噪比下,WCMSR方法的空间谱中出现杂乱的谱峰,使得该方法在低信噪比下几乎失效,其它两种基于稀疏性的方法的估计精度高于基于信号子空间的估计方法,其中由于ATh- MDSBL方法能够利用自适应门限处理方法,抑制幅度较大的干扰信号,因此ATh-MDSBL方法的估计精度高于NTh-MDSBL方法。随着信噪比的增大,WCMSR方法的估计性能大幅度地提升,但是由于基于范数的稀疏重构方法无法保证解的全局最优性,最终的估计精度不如NTh-MDSBL方法和ATh- MDSBL方法。

图 3 均方根误差随信噪比的变化曲线
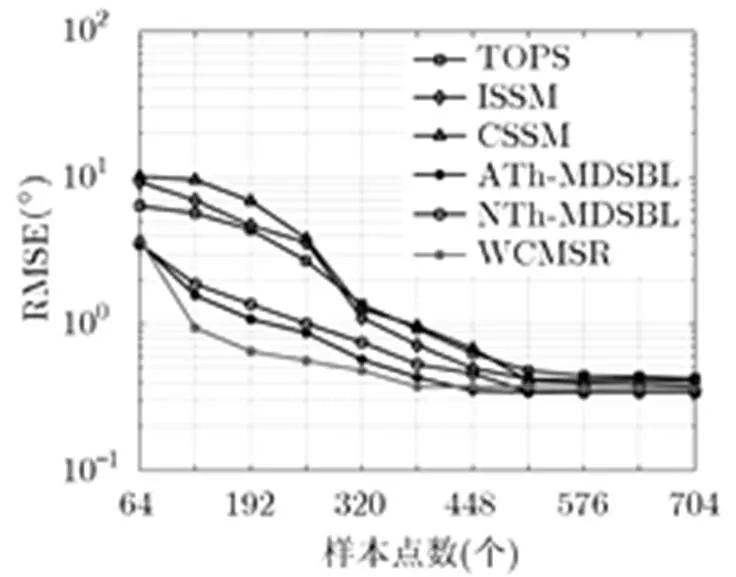
图 4 均方根误差随样本点数的变化曲线
最后,验证本文基于ATh-MDSBL方法、文献[12]LRMAP方法和文献[20]GLR方法的检测性能。假设两个信号信噪比均为,样本点总数为320点,其中每个数据段包含64个样本点。图5展示了3种算法的ROC性能曲线。由于LRMAP检测算法利用了信号的空域稀疏性,算法性能优于GLR检测算法。对比LRMAP和SBL性能曲线看出,本文检测算法构造的判决统计量相比于文献[12]具有更好的检测性能。
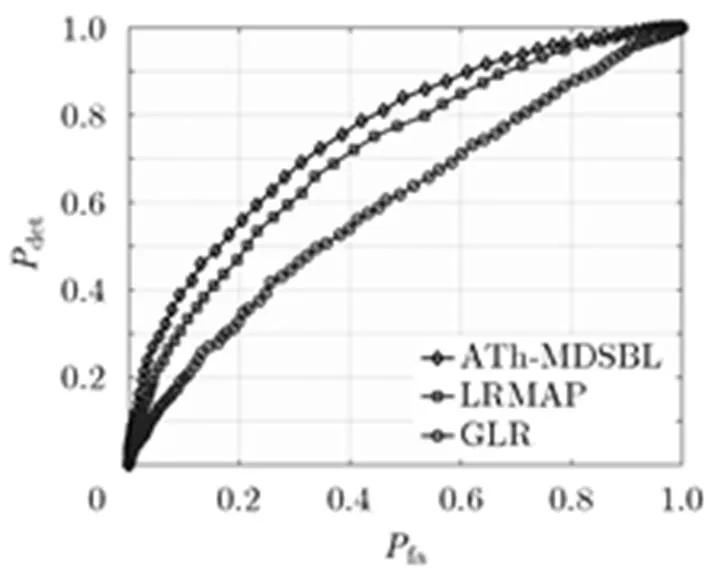
图 5 不同检测算法的ROC性能曲线
保持虚警概率为1%,在相同的样本点数条件下观察信噪比对检测概率的影响。如图6所示,在低信噪比条件下GLR检测算法的性能最差。对比LRMAP和本文检测算法的性能曲线可以得出,后者能够更好地适应于低信噪比条件,当信噪比大于时检测概率能够达到80%以上。
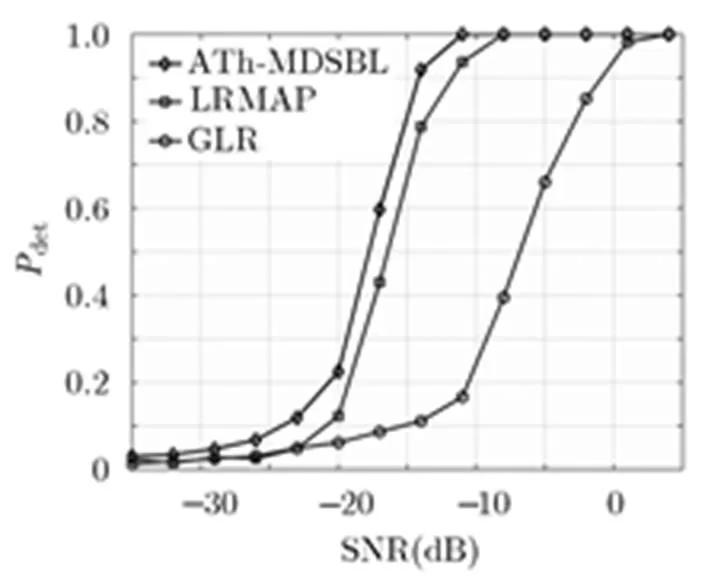
图 6 不同算法的检测概率随信噪比的变化曲线
7 结束语
本文将信号的角度信息引入到频谱检测问题中,对于在时域和频域上发生混叠的多信号具有较好的检测和识别能力。根据信号在角度域的稀疏特性构造多字典稀疏模型,在利用传统SBL算法解决稀疏重构问题的基础上,引入一种自适应判决的处理方法。该方法在恒虚警概率条件下对每一个预设来波方向进行信号检测,克服了传统稀疏重构方法重构精度低和运算复杂度高的缺陷。通过与传统的宽带DOA估计算法比较发现,算法在低信噪比和小样本条件下可以得到更加精确的角度估计值。此外,算法的整体检测性能相比于现有方法具有较为明显的增强,提高了频谱检测算法在低信噪比条件下的适应能力。
[1] DIKMESE S, SOFOTASIOS P C, IHALAINEN T,. Efficient energy detection methods for spectrum sensing under non-flat spectral characteristics[J]., 2015, 33(5): 755-770. doi: 10.1109/JSAC.2014.2361074.
[2] 马彬, 方源, 谢显中. 一种主用户随机到达情况下改进的循环平稳特征检测算法[J]. 电子与信息学报, 2015, 37(7): 1531-1537. doi: 10.11999/JEIT141283.
MA Bin, FANG Yuan, and XIE Xianzhong. Improved cyclostationary spectrum sensing scheme for primary users randomly arriving[J].&, 2015, 37(7): 1531-1537. doi: 10.11999/JEIT 141283.
[3] ZHANG Xinzhi, CHAI Rong, and GAO Feifei. Matched filter based spectrum sensing and power level detection for cognitive radio network[C]. IEEE Global Conference on Signal and Information Processing. Atlanta, USA, 2014: 1267-1270.
[4] WILCOX D, TSAKALAKI E, KORTUN A,. On spatial domain cognitive radio using single-radio parasitic antenna arrays[J]., 2013, 31(3): 571-580. doi: 10.1109/JSAC. 2013.130321.
[5] 赵晓晖, 李晓燕. 认知无线电中基于阵列天线和协方差矩阵的频谱感知算法[J]. 电子与信息学报, 2014, 36(7): 1693-1698. doi: 10.3724/SP.J.1146.2013.01057.
ZHAO Xiaohui and LI Xiaoyan. Spectrum sensing algorithm in cognitive radio based on array antenna and covariance matrix[J].&2014, 36(7): 1693-1698. doi: 10.3724/SP.J.1146.2013.01057.
[6] 马启明, 王宣银, 杜栓平. 基于频谱幅度起伏特性的微弱信号检测方法研究[J]. 电子与信息学报, 2008, 30(11): 2642-2645.
MA Qiming, WANG Xuanyin, and DU Shuanping. Research of the method for the weak signal detection based on the amplitude fluctuation property of the frequency spectrum[J].&, 2008, 30(11): 2642-2645.
[7] 刘畅, SYED S A, 张锐, 等. 基于空间谱的多天线盲频谱感知算法[J]. 通信学报, 2015, 36(4): 119-128. doi: 10.11959/j.issn. 1000-436x.2015087.
LIU Chang, SYED S A, ZHANG Rui,Spatial spectrum based blind spectrum sensing for multi-antenna cognitive radio system[J]., 2015, 36(4): 119-128. doi: 10.11959/j.issn.1000-436x.2015087.
[8] 左加阔, 陶文凤, 包永强, 等. 多跳认知水声通信中的分布式稀疏频谱检测算法[J]. 电子与信息学报, 2013, 35(10): 2359-2364. doi: 10.3724/SP.J.1146.2013.00042.
ZUO Jiakuo, TAO Wenfeng, BAO Yongqiang,. Distributed sparse spectrum detection in multihop cognitive underwater acoustict communication networks[J].&, 2013, 35(10): 2359-2364. doi: 10.3724/SP.J.1146.2013.00042.
[9] HUANG Dinhwa, WU Sauhsuan, WU Wenrong,. Cooperative radio source positioning and power map reconstruction: a sparse bayesian learning approach[J]., 2015, 64(6): 2318-2332. doi: 10.1109/TVT.2014.2345738.
[10] LEI Chuan, ZHANG Jun, and GAO Qiang. Detection of unknown and arbitrary sparse signals against noise[J]., 2014, 8(2): 146-157. doi: 10.1049/iet-spr. 2011.0125.
[11] WACHOWSKI N and AZIMI M R. Detection and classification of nonstationary transient signals using sparse approximations and bayesian networks[J]./, 2014, 22(12): 1750-1764. doi: 10.1109/TASLP.2014.2348913.
[12] PARIS S, MARY D, and FERRARI A. Detection tests using sparse models, with application to hyperspectral data[J]., 2013, 61(6): 1481-1494. doi: 10.1109/TSP.2013.2238533.
[13] ZHOU Yifeng, YIP P C, and LEUNG H. Tracking the direction-of-arrival of multiple moving targets by passive arrays: algorithm[J]., 1999, 47(10): 2655-2666.
[14] WIPF D P and RAO B D. An empirical bayesian strategy for solving the simultaneous sparse approximation problem[J].2007, 55(7): 3704-3716. doi: 10.1109/TSP.2007.894265.
[15] WIPF D P, RAO B D, and NAGARAJAN S. Latent variable Bayesian models for promoting sparsity[J].2011, 57(9): 6236-6255. doi: 10.1109/TIT.2011.2162174.
[16] KELLY E J and FORSYTHE K M. Adaptive detection and parameter estimation for multidimensional signal models[R]. Lexington: Lincoln Lab, 1989.
[17] TIPPING M E. Sparse bayesian learning and the relevance vector machine[J].2001, 1(3): 211-244.
[18] 刘寅, 吴顺君, 吴明宇, 等. 基于空域稀疏性的宽带DOA估计[J]. 航空学报, 2012, 33(11): 2028-2038.
LIU Yin, WU Shunjun, WU Mingyu,. Wideband DOA estimation based on spatial sparseness[J]., 2012, 33(11): 2028-2038.
[19] LIU Zhangmeng, HUANG Zhitao, and ZHOU Yiyu. Direction-of-Arrival estimation of wideband signals via covariance matrix sparse representation[J].2011, 59(9): 4256-4270. doi: 10.1109/TSP.2011.2159214.
[20] KAY S M and GABRIEL J R. An invariance property of the generalized likelihood ratio test[J]., 2003, 10(12): 352-355. doi: 10.1109/LSP.2003. 818865.
Adaptive Spectrum Detection Algorithm Based on Spatial Sparsity
YU Hongyi CHENG Biao HU Yunpeng SHEN Zhixiang
(,,450002,)
The existing spectrum detection method can not take full advantage of angle dimension. To sense the spectrum more comprehensively, the signal model is established based on the sparsity of angle dimension. The reconstruction result can be derived by Sparse Bayesian Learning (SBL) algorithm. By integrating the binary probability hypothesis into iterative procedure of SBL, a decision test combined with adaptive threshold is derived. The proposed pruning step can accept the active components of the model, and transform the sparse recovery into a detection problem for signals from different angles. Therefore, the algorithm can sense the spectrum blindly with constant false-alarm rate as well as estimate the accurate angle of each incident signal. Numerical simulation results verify that adaptive threshold can improve reconstruction accuracy with low computing cost. Moreover, the proposed algorithm can achieve better estimation and detection performance than previous algorithms.
Spectrum detection; Sparse Bayesian Learning (SBL); Constant false-alarm rate; Adaptive threshold
TN911.7
A
1009-5896(2016)07-1703-07
10.11999/JEIT151030
2015-09-10;改回日期:2016-01-22;网络出版:2016-03-29
程标 chengb_cn@163.com
国家自然科学基金(61501517)
The National Natural Science Foundation of China (61501517)
于宏毅: 男,1963年生,博士,教授,博士生导师,主要研究方向为无线通信、无线传感器网络等.
程 标: 男,1990年生,硕士,主要研究方向为无线通信、通信信号处理.
胡赟鹏: 男,1978年生,博士,副教授,硕士生导师,主要研究方向为通信信号处理、无线传感器网络等.
沈智翔: 男,1985年生,博士,讲师,主要研究方向为通信信号处理、多天线信号合成技术.
