极大平面图的结构与着色理论 (4)-运算与Kempe等价类

许 进



极大平面图的结构与着色理论 (4)-运算与Kempe等价类

许 进*

(北京大学高可信软件技术教育部重点实验室 北京 100871),(北京大学信息科学技术学院 北京 100871)

设是一个-色图，若的所有-着色是Kempe等价的，则称为Kempe图。表征色数的Kempe图特征是一尚待解决难题。该文对极大平面图的Kempe等价性进行了研究，其主要贡献是：(1)发现导致两个4-着色是Kempe等价的关键子图为2-色耳，故对2-色耳的特征进行了深入研究；(2)引入-特征图，清晰地刻画了一个图中所有4-着色之间的关联关系，并深入研究了-特征图的性质；(3)揭示了4-色非Kempe极大平面图的Kempe等价类可分为树型，圈型和循环圈型，并指出这3种类型可同时存在于一个极大平面图的4-着色集中；(4)研究了Kempe极大平面图特征，给出了该类图的多米诺递推构造法，以及两个Kempe极大平面图猜想。

Kempe极大平面图；Kempe变换；-运算；Kempe等价类；-特征图；2-色耳

1 引言

无论是理论上还是应用上，平面图都是一类非常重要的图类。理论方面，著名的4-色猜想，唯一4-色平面图猜想，9-色猜想，及3-色问题等[1]不仅在图论领域，乃至整个数学界都具有重大影响；从应用的角度来讲，平面图理论可直接应用于电路布线[2]，信息科学[3]等领域。

极大平面图是平面图中一类重要的图类，它的每个面的边界均为三角形，故也称为三角剖分图。由于著名的4-色猜想的研究对象可归为极大平面图，因此，100多年来，关于极大平面图的研究吸引了众多学者，他们围绕着4-色猜想，相继研究了度序列，构造，着色特性，可遍历性，生成运算等诸多方面[4]。并且在研究过程中，提出了诸如唯一4-色极大平面图猜想以及9-色猜想等，它们也逐渐构成了极大平面图着色理论的核心研究目标。

在极大平面图的着色性质与结构方面，一项很重要的工作是Kempe变换与Kempe等价类。Kempe变换是指在一个着色图中，将某个2-色导出子图的某个连通分支上的颜色互换，其余顶点的着色不变的一种颜色变换方法。本文所定义的-运算是指在4-着色下的包含一次或多次Kempe变换的运算(详见第3节)。-运算是一种导色运算：从中的一个4-着色导出的另一个4-着色。

Kempe变换始于1879年Kempe的工作[5]。自Kempe之后，首先对Kempe等价类进行系统研究的是Fisk，他在1977年文献[6]中证明了：当一个极大平面图的顶点度数均为偶数时，其所有4-着色构成一个Kempe等价类；1978年，Meyniel证明了：任一平面图的所有5-着色构成一个Kempe等价类[7]；1981年，Vergnas与Meyniel证明了：不可收缩至的任一简单图的所有5-着色是一个Kempe等价类[8]；2007年，Mohar证明了：每个色数小于的平面图，其所有-着色是Kempe等价的[9]，并提出了下列猜想：

2015年，Feghali等人[10]证明了猜想1在时，除或三角柱外，立方体图的所有3-着色是Kempe等价的；我们证明了当时，猜想1成立1)；当时，此猜想尚待解决。

2008年，Cereceda等人[11]对的-色特征图进行了研究，其中，的顶点集为的所有-着色构成的集合，两个-着色相连边当且仅当它们在中仅有一个顶点着不同颜色，并证明了：当的色数时，不连通；当时，可能连通，也可能不连通。

类似于顶点着色，一些学者对边着色的Kempe变换与Kempe等价类进行了研究，如Mcdonald等人[12]，Sarah等人[13]等。

有关Kempe变换与Kempe等价类的图算法复杂度的研究进展可参见文献[14-24]。

本系列文章意在建立极大平面图着色运算系统，该系统有两种导色运算：一种是-运算，另一种是-运算，也称为伪边导色法(另行文)。而在一个极大平面图中，-运算一般不能从一个4-着色导出所有4-着色，或所需的4-着色，但-运算可从中的一个4-着色导出所有的4-着色，或所需4-着色。

如果一个图能够画在平面上使得它的边仅在顶点相交，则称这个图为平面图。平面图的这种画法称为它的一个平面嵌入，本文所研究的平面图均指基于它的一个平面嵌入的平面图。对于一个平面图，如果只要任何两个不相邻的顶点之间再加一条边，其平面性一定被破坏，则称该平面图为极大平面图。若一个平面图的每个面(包括无穷面)都由3条边界组成，则称该平面图为三角剖分图。易证，极大平面图和三角剖分图是等价的。

把图1中所示的图称为漏斗，其中度数为1的顶点称为漏顶；度数为3的顶点称为漏腰；两个度数为2的顶点称为漏底。若一个图的顶点导出子图是漏斗，则该子图称为漏斗子图。更详细论述见本系列文章(2)[25]。

图1 漏斗

文中未给出的相关定义、记号与理论参见文献[25-27]。

2 2-色耳

本节先对2-色圈给予描述与分类，在此基础上给出2-色耳的定义与结构等。2-色耳是可连续施行-运算的根源。

2.1 2-色圈相关定义

图2 弦圈、弦路圈与基本圈

图3两个2-色圈相关的情况

2.2 2-色耳的相关定义与性质

图4 耳朵、同根耳、同源耳说明示意图

证毕

图5 成圈的同色耳结构示意图，其中实线表示

文献[26]中引入了树着色与圈着色的概念，为方便，在此重述如下。设是一个4-色极大平面图，,为颜色集。若，使得中含圈，则称为圈着色，并称为可圈着色的；反之，若,中均无圈，则称为图的树着色，并称为可树着色的；若是可树着色，但非可圈着色，则称为纯树着色的；若是可圈着色，但非可树着色，则称为纯圈着色的；若既是可圈着色，又是可树着色，则称为混合型着色的。由圈着色与树着色的定义，对任一4-色极大平面图，可将中的着色分为两类：圈着色与树着色。

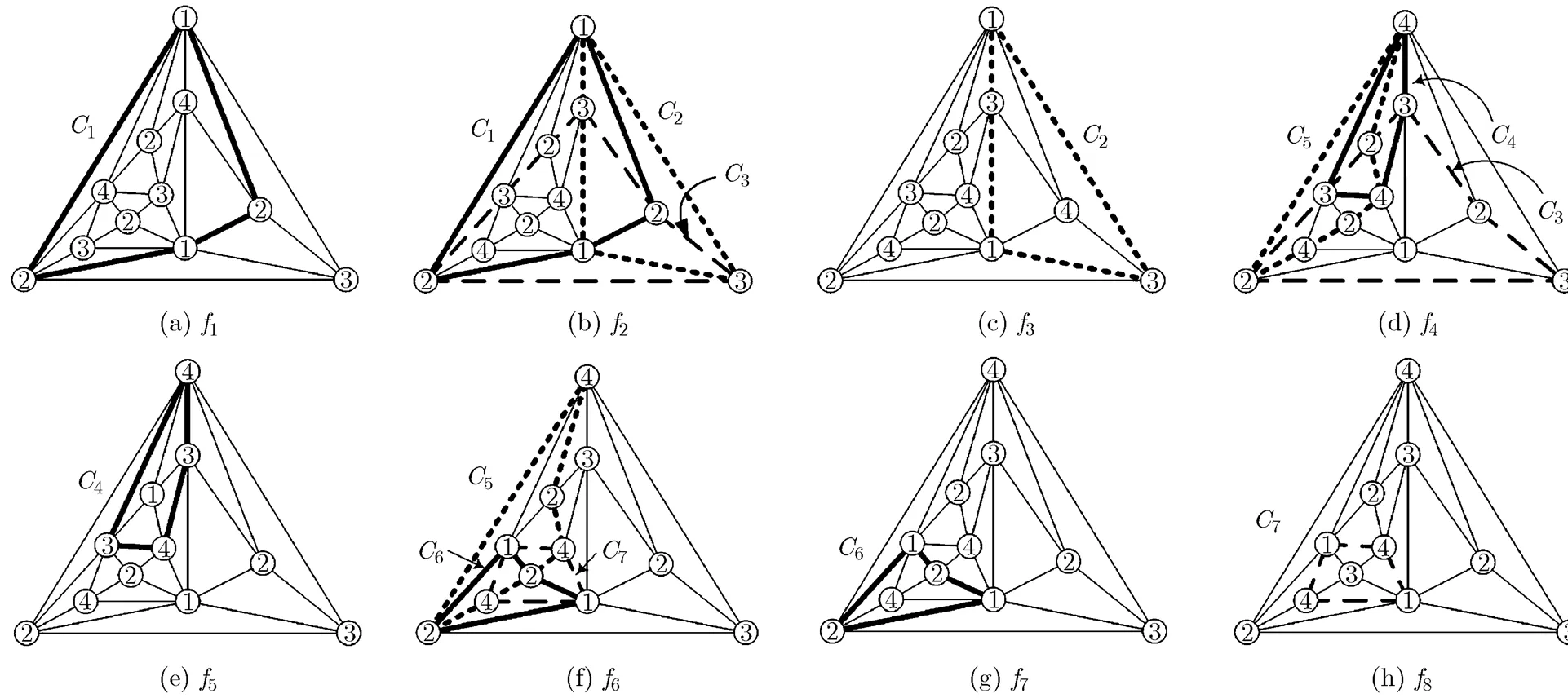
图6 -运算示例

图7 图6中所示图的-特征图

对于阶数不超过11的所有极大平面图，树着色的数目约占2%[26]。故我们推测对最小度的极大平面图集，树着色数相比圈着色数来说非常少，因此，给定4-色极大平面图的一个圈着色，很有可能通过-运算将中的其它着色推导出来。

图8 不相交的情况

如下2种情况给予证明：

图9 相交的情况

基于上述两种情况，本定理获证。

图10 定理6证明示意图

4 非Kempe图的Kempe等价类类型

4.1 树型Kempe等价类

由此推出定理8：

4.2 圈型Kempe等价类

图12中分别给出了两个都含2个2-色不变圈的极大平面图，其中第1个图中的2个2-色不变圈有两个公共顶点。图12(a)-图12(j)给出了该图的所有4-着色，且在图12(k)给出了它的-特征图。图12(l)给出了含不相交的2个2-色不变圈(用粗线标记)的极大平面图。

4.3 循环圈型Kempe等价类

图13 圈型及循环型圈型Kempe等价类的两个例子

纯圈型，即含1个或多个2-色不变圈，如图11，图12所示的图；

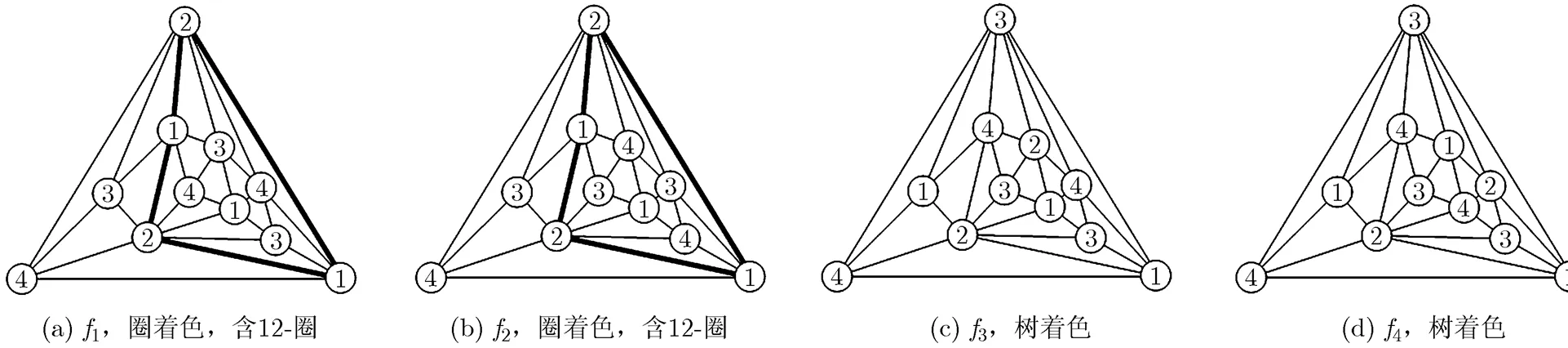
图11 只含有一个2-色不变圈的圈型极大平面图

图12 含2个2-色不变圈的圈型极大平面图

混合型，即既含2-色不变圈型，又含循环圈型，如图13(a)；

纯循环圈型，即只含1个或多个循环2-色圈，如图13(c)中所给出的4-着色，它同时含2个循环圈型。

注1 有些图在不同着色下含相同的某2-色圈，但这些着色并不属于同一Kempe等价类。

注2 由上述给出3种Kempe等价类可知，在一个给定的最小度的极大平面图中，中可能存在1~3种Kempe等价类，且可能存在多个同种类型的Kempe等价类。如正20面体含有10个树型等价类。

5 Kempe图

5.1 Kempe图猜想

此猜想与唯一4-色极大平面图猜想息息相关。若唯一4-色极大平面图猜想成立，即每个唯一4-色极大平面图是递归极大平面图[26]，则最小度的4-色极大平面图至少有2种不同的4-着色。若是树型，由于树着色不能通过-运算到达的其它4-着色，因此一定不是Kempe图。

即使猜想3成立，也不能仅从Kempe图所含等价类的类型来确定Kempe图的特征。为深入研究Kempe图的特征，我们提出了多米诺递推构造法。

5.2 Kempe图的构造

由本系列文章(2)[25]知：一个最小度的-阶极大平面图，其祖先图集中必含-阶，或-阶最小度的极大平面图。换言之，中至少存在图14中的5个基本多米诺构形之一。为方便，本系列文章将5个基本多米诺构形分别标记为,,,,，如图14所示。

图14 5个基本多米诺构形

关于Kempe极大平面图更为深入的研究将在后续文章中给出，其中包括定理11的详细论证，猜想4的论证，以及与的关系等的研究。

6 结束语

众所周知，表征Kempe图的特征一直是图着色理论与算法研究中的难点与热点问题。目前虽然在此领域中发表了不少学术论文，但是给出一般色数为的Kempe图的充分必要条件仍很困难，故目前学界主要对一些特殊图类的Kempe等价类展开研究，如正则图等。本系列文章主要对另一类图——极大平面图的Kempe等价类展开了研究。

本文的主要贡献是：(1)发现了导致两个4-着色是Kempe等价的关键子图为2-色耳，故对2-色耳的特征进行了深入研究；(2) 引入-特征图，清晰地刻画了图中所有着色之间的关联关系，并对-特征图的性质进行了深入的研究；(3)揭示了非Kempe图的Kempe等价类可分为树型，圈型和循环圈型，并指出这3种类型可同时存在于一个极大平面图的4-着色集中；(4)研究了Kempe图的特征，给出了Kempe图的多米诺递推构造法，并猜想与是Kempe图的充分必要条件是在图中可4-色漏斗子图的个数。

在后续文章中将对3类非Kempe图的结构与特征进行深入研究，特别，将给出Kempe极大平面图的充分必要条件。

致谢 本文在完成过程中，与姚兵教授、陈祥恩教授以及吴建良教授，以及我的6位图论专业学生：王宏宇(博士生)，刘小青(博士生)，朱恩强(博士后)，李泽鹏(博士后)，周洋洋(硕士生)，以及赵栋杨(硕士生)等进行了多次有益讨论，在此表示感谢。最后，特别感谢北京大学何新贵院士、余道衡教授对本文的审阅，以及对作者的鼓励、鞭策与支持。

[1] JENSEN T R and TOFT B. Graph coloring problems[J].-, 1995, 113(2): 29-59. doi: 10.1002/ 9781118032497.ch2.

[2] DIAZ J, PETIT J, and SERNA M. A survey of graph layout problems[J]., 2002, 34(3): 313-356. doi: 10.1145/568522.568523.

[3] BRODER A, KUMAR R, MAGHOUL F,Graph structure in the web[J]., 2000, 33(1/6): 309-320. doi: 10.1016/S1389-1286(00)00083-9.

[4] 许进, 李泽鹏, 朱恩强. 极大平面图理论研究进展[J]. 计算机学报, 2015, 38(8): 1680-1704. doi: 10. 11897/SP.J.1016.2015. 01680.

XU J, LI Z P, and ZHU E Q. Research progress on the theory of maximal planar graphs[J]., 2015, 38(8): 1680-1704. doi: 10.11897/SP.J.1016.2015. 01680.

[5] KEMPE A B. On the geographical problem of the four colors[J]., 1879, 2(3): 193-200. doi: 10.2307/2369235.

[6] FISK S. Geometric coloring theory[J].,1977, 24(3): 298-340. doi: 10.1016/0001- 8708(77)90061-5.

[7] MEYNIEL H. Les 5-colorations d'un graphe planaire Forment une classe de commutation unique[J]., 1978, 24(3): 251-257. doi: 10.1016/0095-8956(78)90042-4.

[8] VERGNAS M L and MEYNIEL H. Kempe classes and the Hadwiger conjecture[J]., 1981, 31(1): 95-104. doi: 10.1016/S0095- 8956(81)80014-7.

[9] MOHAR B. Kempe Equivalence of Colorings[M]. Graph Theory in Paris, Birkhäuser Basel, 2006: 287-297. doi: 10.1007/978-3-7643-7400-6_22.

[10] FEGHALI C, JOHNSON M, and PAULUSMA D. Kempe equivalence of colourings of cubic graphs[J]., 2015, 49: 243-249. doi: 10.1016/j. endm.2015.06.034.

[11] CERECEDA L, HEUVEL J V D, and JOHNSON M. Connectedness of the graph of vertex-colourings[J]., 2008, 308(5/6): 913-919. doi: 10.1016/j.disc. 2007.07.028.

[12] MCDONALD J, MOHAR B, and SCHEIDE D. Kempe equivalence of edge-colorings in subcubic and subquartic graphs[J]., 2012, 70(2): 226-239. doi: 10.1002/jgt.20613.

[13] BELCASTRO S M and HAAS R. Counting edge-Kempe- equivalence classes for 3-edge-colored cubic graphs[J]., 2014, 325(13): 77-84. doi: 10.1016/j. disc.2014.02.014.

[14] FIOL M A and VILALTELLA J. A simple and fast heuristic algorithm for edge-coloring of graphs[J]., 2013, 10(3): 263-272.

[15] EFTHYMIOU C and SPIRAKIS P G. Random sampling of colourings of sparse random graphs with a constant number of colours[J]., 2008, 407(1/3): 134-154. doi: 10.1016/j.tcs.2008.05.008.

[16] DYER M, FLAXMAN A D, FRIEZE A M,. Randomly coloring sparse random graphs with fewer colors than the maximum degree[J]., 2006, 29(4): 450-465. doi: 10.1002 /rsa.20129.

[17] HAYES T P and VIGODA E. A non-Markovian coupling for randomly sampling colorings[C]. 44th Annual Symposium on Foundations of Computer Science, 2003: 618-627. doi: 10.1109/SFCS.2003.1238234.

[18] LUCZAK T and VIGODA E. Torpid mixing of the Wang- Swendsen-Kotecky algorithm for sampling colorings[J]., 2005, 3(1): 92-100. doi: 10.1016/j.jda.2004.05.002.

[19] MORGENSTERN C A and SHAPIRO H D. Heuristics for rapidly four-coloring large planar graphs[J]., 1991, 6(1): 869-891. doi: 10.1007/BF01759077.

[20] SIBLEY T and WAGON S. Rhombic penrose tilings can be 3-colored[J]., 2000, 107(3): 251-253. doi: 10.2307/2589317.

[21] VIGOD E. Improved bounds for sampling colorings[C]. 40th Annual Symposium on Foundations of Computer Science, New York, 1999: 51-59. doi: 10.1109/SFFCS.1999.814577.

[22] FRIEZE A and VIGODA E. A survey on the use of markov chains to randomly sample colourings[C]. In Combinatorics, Complexity, and Chance. Oxford Lecture Ser. Math. Appl. 34 53-71. Oxford Univ. Press, Oxford. MR2314561doi: 10.1093/acprof:oso/9780198571278.003.0004.

[23] HAYES T P and VIGODA E. Coupling with the stationary distribution and improved sampling for colorings and independent sets[J]., 2006, 16(3): 1297-1318. doi: 10.1214/105051606000000330.

[24] BALASUBRAMANIAN R and SUBRAMANIAN C R. On sampling colorings of bipartite graphs[J]., 2006, 8(1): 17-30.

[25] 许进. 极大平面图的结构与着色理论(2): 多米诺构形与扩缩运算[J]. 电子与信息学报, 2016, 38(6): 1271-1327. doi: 10.11999/JEIT160224.

XU J. Theory on structure and coloring of maximal planar graphs (2): Domino configurations and extending- contracting operations[J].&, 2016, 38(6): 1271-1327. doi: 10.11999/JEIT160224.

[26] 许进. 极大平面图的结构与着色理论(3): 纯树着色与唯一4-色平面图猜想[J]. 电子与信息学报, 2016, 38(6): 1328-1353. doi: 10.11999/JEIT160409.

XU J. Theory on structure and coloring of maximal planar graphs (3): Purely Tree-colorable and Uniquely 4-colorable Maximal Planar Graph Conjectures[J].&, 2016, 38(6): 1328-1353. doi: 10.11999/JEIT160409.

[27] BONDY J A and MURTY U S R. Graph Theory[M]. Springer, 2008: 6-58.

Theory on Structure and Coloring of Maximal Planar Graphs (4)-Operations and Kempe Equivalent Classes

XU Jin

(,,100871,),(,,100871,)

Letbe a-chromatic graph.is called a Kempe graph if all-colorings ofare Kempe equivalent. It is an unsolved and hard problem to characterize the properties of Kempe graphs with chromatic number. The Kempe equivalence of maximal planar graphs is addressed in this paper. Our contributions are as follows: (1) Observe and study a class of subgraphs, called 2-chromatic ears, which play a critical role in guaranteeing the Kempe equivalence between two 4-colorings; (2) Introduce and explore the properties of-characteristic graphs, which clearly characterize the relations of all 4-colorings of a graph; (3) Divide the Kempe equivalent classes of non-Kempe 4-chromatic maximal planar graphs into three classes, tree-type, cycle-type, and circular-cycle-type, and point out that all these three classes can exist simultaneously in the set of 4-colorings of one maximal planar graph; (4) Study the characteristics of Kempe maximal planar graphs, introduce a recursive domino method to construct such graphs, and propose two conjectures.

Kempe maximal planar graph, Kempe transformation,-operation, Kempe equivalent class,-characteristic graph, 2-chromatic ear

O157.5

A

1009-5896(2016)07-1557-29

10.11999/JEIT160483

2016-05-11；改回日期：2016-05-30；网络出版：2016-06-02

：许进 jxu@pku.edu.cn

国家973计划项目(2013CB329600)，国家自然科学基金(61372191, 61472012, 61472433, 61572046, 61502012, 61572492, 61572153, 61402437)

The National 973 Program of China (2013CB 329600), The National Natural Science Foundation of China (61372191, 61472012, 61472433, 61572046, 61502012, 61572492, 61572153, 61402437)

1)LIU Xiaoqing, XU Jin, submitted to Discrete Mathematics.

许 进： 男，1959年生，教授，主要研究领域为图论与组合优化、生物计算机、社交网络与信息安全等.