机载雷达自适应对角加载参数估计方法

姜 磊 王 彤



机载雷达自适应对角加载参数估计方法

姜 磊 王 彤*

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

对角加载可以提高空时自适应处理在低样本情况下的性能。然而，在实际中加载参数的确定是一个较为困难的问题。为了解决这个问题，该文提出一种基于回波数据的自适应对角加载参数估计方法。该方法首先将对角加载问题转化为Tikhonov规划问题，然后利用广义交叉验证准则构造优化问题，最后采用割线法求解优化问题、计算加载参数。仿真与实测数据结果表明该方法可以有效提高机载雷达在低样本条件下的目标检测性能。

目标检测；空时自适应处理；对角加载；参数估计；广义交叉验证；割线法

1 引言

空时自适应处理(STAP)是一种联合空域和时域的滤波方法，其可以有效地抑制地面杂波，提高机载雷达对运动目标的检测能力。STAP在计算自适应滤波权值矢量时，需要利用杂波分布和噪声分布的期望协方差矩阵。实际情况中期望协方差矩阵无法获得，这时STAP通常利用距离维的数据作为训练样本来对协方差矩阵进行估计。当训练样本数目充足且满足独立同分布的条件时，估计的协方差矩阵可以收敛于期望协方差矩阵，此时自适应滤波可以取得较好的性能。因此，协方差矩阵的估计在STAP中占有重要的位置。

机载雷达在实际中面临的杂波环境常常呈现非均匀性。地表覆盖类型变化、地形高程起伏、样本中的目标信号以及强杂波离散点等破环了训练样本的均匀假设，这些非理想的因素使得接收数据的统计特性随时间和空间产生变化。在这种情况下，机载雷达获取大量的独立同分布的样本是不切实际的。当均匀样本数目不足时，估计的协方差矩阵相对于真实的协方差矩阵会产生较大的偏差，从而导致机载雷达的杂波抑制与目标检测性能下降。

为了克服均匀样本数目不足的问题，研究人员提出了多种解决办法。文献[4,5]提出了降秩处理方法。该方法是一种基于特征子空间的方法，其利用了空时协方差矩阵的低秩特性。然而，杂波秩的确定是一个较为复杂的问题。由于杂波子空间的泄漏问题，按照理论计算的杂波秩与实际的杂波秩不一致，从而造成降秩方法性能下降。文献[6,7]提出了基于稀疏恢复的直接数据域方法。该方法利用空时快拍数据在角度多普勒域的稀疏性，采用稀疏恢复的方法获得杂波的空时2维谱，接着利用空时谱与字典矩阵重构杂波协方差矩阵。然而，阵元误差和通道误差[8]导致了构造的字典矩阵与实际的数据不匹配，从而造成了稀疏恢复的空时谱的不准确及重构的协方差矩阵的误差。文献[9]提出了基于对角加载的协方差矩阵估计方法。该方法通过融合采样协方差矩阵与结构化的对角矩阵来提高协方差矩阵的估计精度，该方法运算量低、实用性强，在稳健波束形成[10]与动目标检测[11]等方面均取得了明显的增益。

对角加载参数通常可以根据雷达系统的噪声功率水平来确定。然而，实际工程应用中噪声功率的实时、准确测定是一个复杂的问题。为此，本文提出了一种基于回波数据的自适应的加载参数估计方法，该方法利用广义交叉验证(Generalized Cross Validation, GCV)准则来计算加载参数。仿真与实测数据实验结果表明该方法可以准确地估计加载参数，有效提高了机载雷达在低样本条件下的目标检测性能。

2 对角加载原理

机载雷达通常采用STAP技术来检测杂波背景下的运动目标。STAP是一种空时2维的自适应滤波器，接收数据经过STAP处理后的输出为

式(3)为线性约束最小方差(Linearly Constrained Minimum Variance, LCMV)问题，对应的解为

当训练样本满足独立同分布的条件并且样本数目大于两倍的滤波器自由度时，自适应滤波相对于最优滤波的性能损失不超过3 dB。然而，实际中由于杂波的非均匀性，STAP可以利用的均匀样本数目是受到限制的。当均匀样本数目不足时，协方差矩阵估计精度下降，利用式(4)计算出的权值矢量将不能有效地滤除数据中的杂波分量，从而导致了STAP的目标检测性能下降。

为了减小协方差矩阵估计误差，提高STAP在样本数目不足条件下的性能，研究人员提出了对角加载技术。对角加载是一种对采样协方差矩阵的特征值优化的方法[12]，其可以表示为式(5)的约束优化问题。

式(5)进行整理可以得到

利用拉格朗日乘子法，可以得到式(6)对应的解为

由式(7)可以看出对角加载表现为在采样协方差矩阵上加上一个尺度化的对角矩阵，其中加载参数的数值大小直接影响了滤波器权值矢量。若取值过小，则对角加载作用变得忽略不计；若取值过大，则自适应滤波退化为非自适应滤波。因此，选择一个合适的加载参数是一个十分关键的问题。文献[13]指出，在实际的工程应用中，可以根据雷达系统的噪声功率水平来确定。这就意味着在进行对角加载之前，需首先获取噪声功率水平这一参数。然而，在实际中噪声功率受到时间灵敏度控制器(Sensitivity Time Control, STC)、带通滤波器、自动增益控制(Automatic Gain Control, AGC)以及模拟/数字转换器(Analog-to-Digital Converter, ADC)等多种设备的影响，对其实时、准确测定是一件较为复杂的任务。因此，有必要研究一种自适应的对角加载参数估计方法。

3 基于GCV的加载参数估计方法

利用矩阵操作，式(8)可以整理表示为

利用LCMV与广义旁瓣相消(Generalized Sidelobe Canceller, GSC)的等价性。将式(6)对应的约束优化问题转化为以下无约束优化问题，其形式为

将式(10)展开可以得到

(15)可以重新表示为

式(16)为一个标准的Tikhonov规划问题[14]，为该问题对应的罚函数系数。优化问题式(16)具有解析解，对应的形式为

然而，由式(18)可以看出，该优化问题在求解时涉及到矩阵求逆操作以及线性搜索操作。当机载雷达的阵元数与脉冲数较大时，求逆的运算量较大。此外，为了保证参数估计的准确性，线性搜索时的网格密度需设置较大，这进一步增加了算法的运算量，从而限制了自适应加载方法的实用性。因此，针对优化问题式(18)，本文提出一种快速的求解方法。

接着将式(19)与式(21)代入式(18)中目标函数的分子中，可以得到分子部分函数为

开，可以得到

同理，将式(19)代入式(18)中目标函数的分母中，可以得到分母部分函数为

根据矩阵迹的性质，即

式(26)可以表示为

由式(30)可以看出，目标函数的计算仅涉及到复乘与复加操作，无求逆操作，可以说运算量大为降低。然而，线性搜索式的最优值求解运算量较大。为了进一步降低算法复杂度，本文采用割线法[16]搜索式(30)中目标函数的最值。

利用分式的微分性质，可以得到目标函数的导数为

本文所提出的方法主要步骤如图1所示。

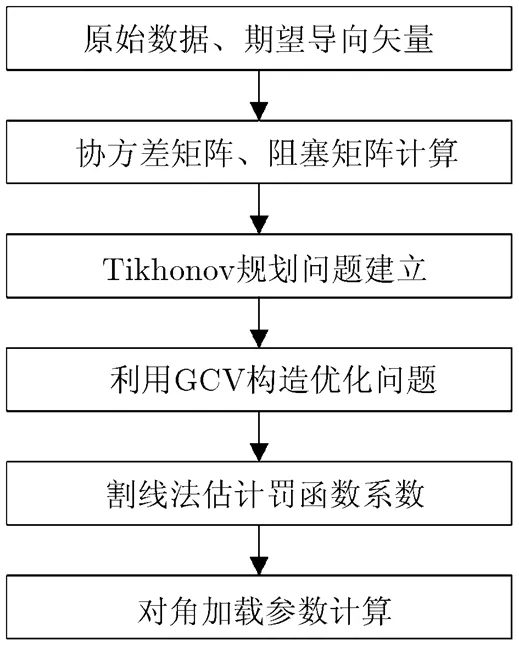
图 1 自适应对角加载参数估计方法流程图

4 仿真与实测数据实验

本节采用仿真数据与实测数据处理实验验证本文所提方法的性能。

4.1 仿真数据实验

本小节通过计算机仿真数据验证本文方法的性能。仿真参数设置如下：雷达载频为1200 MHz，脉冲重复频率为2000 Hz，发射脉冲数目为10，天线阵元数目为10，阵元间距为0.125 m，载机高度为5 km，载机速度为125 m/s，雷达天线主波束方向与阵面法线方向夹角为0°，噪声功率为0 dB，杂噪比为50 dB。实验中加入一个仿真目标，目标位于第200号距离门，信噪比为0 dB，归一化多普勒频率为0.2。杂波抑制时采用全空时处理方法，训练样本选择待检测单元周围的距离单元，其数目为1倍的滤波器自由度大小(低样本情况)。目标检测时采用序贯恒虚警(Ordered-Statistic Constant False Alarm Rate, OS-CFAR)处理，其中OS-CFAR的参考单元数目为15，保护单元数目为3。实验中将本文提出的自适应对角加载方法，文献[4]提出的特征空间方法，文献[6]提出的稀疏恢复方法以及采样协方差方法进行对比分析。

实验1中考虑理想情况(忽略阵元误差、杂波内部运动等)，分析各个方法性能。实验所得结果如图2所示。由图2可以看出，相对于采样协方差方法，特征空间方法、稀疏恢复方法以及自适应加载方法均能取得较好的性能，可以说这3种方法显著改善了STAP在低样本情况下的目标检测性能。实验1说明了自适应加载方法估计的加载参数数值合适，其有效提高了目标的检测性能。

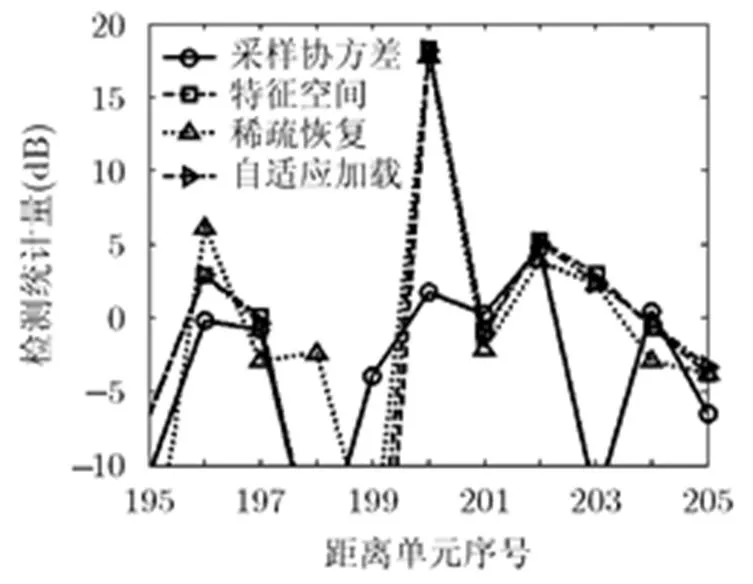
图2 理想情况输出检测统计量

实验2中考虑阵元幅相误差的影响，分析各个方法性能。实验中设置阵元幅度误差为5%，阵元相位误差为，实验所得结果如图3所示。由图3可以看出稀疏恢复方法性能出现明显下降，这是因为稀疏恢复方法是一种模型化的方法，阵元幅相误差导致了构造的字典矩阵与实际的数据失配，造成了稀疏恢复的空时谱的不准确及重构的协方差矩阵的误差，进而使得输出信杂噪比损失增大。特征空间方法和自适应加载方法性能良好，这是因为这两种方法是基于数据的自适应方法。由于接收数据受到阵元幅相误差的调制，从而使得自适应滤波器权值受到相应修正。因此，这两种方法对幅相误差较为稳健。实验2说明了自适应加载方法对幅相误差的稳健性。

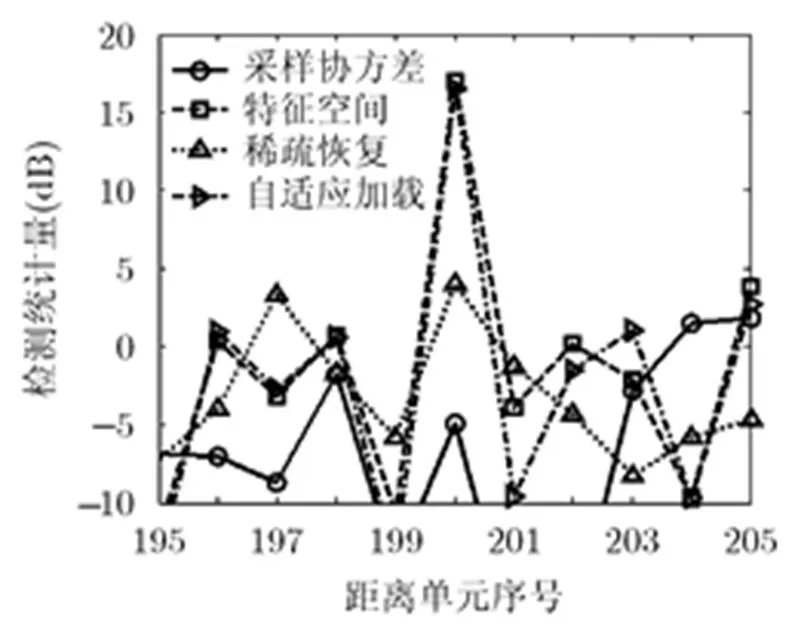
图3 考虑幅相误差时输出检测统计量

实验3中考虑杂波内部运动的影响，分析各个方法性能。杂波内部运动服从Gauss模型，对应的形式为

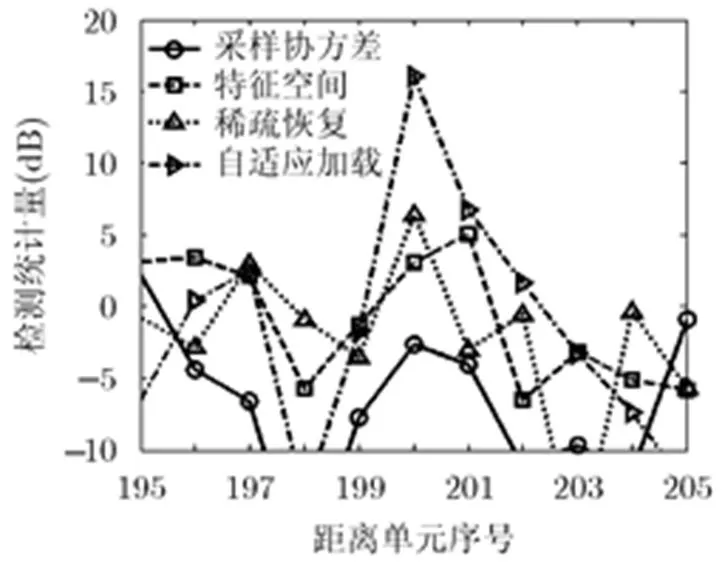
图4 考虑杂波内部运动时输出检测统计量

4.2 实测数据实验

本小节通过机载雷达实测数据验证本文方法的性能。文中采用MCARM计划录取的575数据来进行实验分析。该数据对应的主要雷达系统参数如下所示：雷达载频为1.24 GHz，脉冲重复频率为1984 Hz，相干积累脉冲数为128，方位维通道数为11，方位维通道间距为0.1092 m，俯仰维通道数为2，俯仰维通道间距为0.1407 m，距离单元数目为630。

实验4中分析特征空间方法、稀疏恢复方法、采样协方差方法以及自适应加载方法在低样本情况下的目标检测性能。实验中加入一个仿真目标，目标的距离单元序号为250，归一化多普勒单元频率为0.2，幅度为。实验中选择通道序号为1~11，脉冲序号为1~12的回波数据进行处理。处理过程中采用全空时自适应的方法进行杂波抑制，其中样本选取方式为滑窗处理，样本数目为1倍的滤波器自由度大小。然后采用OS-CFAR检测杂波抑制后的数据，其中OS-CFAR的参考单元数目为15，保护单元数目为3。

图5给出了仿真目标所处多普勒通道的CFAR检测统计量随距离单元序号的变化曲线。由图5可以看出，目标检测性能受到杂波抑制方法的直接影响。本文提出的自适应加载方法性能优于其它3种方法。实验4说明了自适应加载方法的实用性。

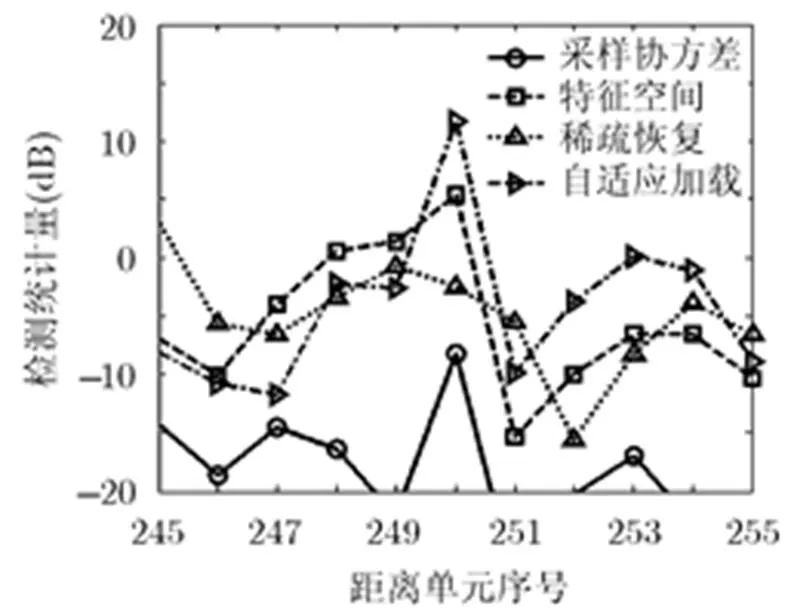
图5 MCARM数据输出检测统计量

5 结束语

本文提出了一种自适应的对角加载参数估计方法。该方法将对角参数估计问题转化为Tikhonov规划罚函数系数估计问题，利用广义交叉验证准则构造优化问题并采用割线法求解优化问题、计算加载参数，从而实现了加载参数的自适应计算。仿真与实测数据实验表明该方法具有良好的参数估计性能并且显著提高了机载雷达在低样本条件下的目标检测性能。

[1] MELVIN W L. A STAP overview[J]., 2004, 19(1): 19-35. doi: 10. 1109/MAES.2004.1263229.

[2] FERTIG L B. Analytical expressions for Space-Time Adaptive Processing (STAP) performance[J]., 2015, 51(1): 442-453. doi: 10.1109/TAES.2014.130676.

[3] 张柏华, 马红光, 孙新利, 等. 基于正交约束的导航接收机空时自适应方法[J]. 电子与信息学报, 2015, 37(4): 900-906. doi: 10.11999/JEIT140740.

ZHANG Baihua, MA Hongguang, SUN Xinli,. Space time adaptive processing technique based on orthogonal constraint in navigation receiver[J].&, 2015, 37(4): 900-906. doi: 10.11999/ JEIT140740.

[4] GUERCI J R, GOLDSTEIN J S, and REED I S. Optimal adaptive reduced-rank STAP[J]., 2000, 36(2): 647-663. doi: 10.1109/7.845255.

[5] ZHU C, LI H B, and RANGASWAMY M. Conjugate gradient adaptive matched filter[J]., 2015, 51(1): 178-191. doi: 10.1109/TAES.2014.130419.

[6] YANG Z C, LI X, WANG H Q,. On clutter sparsity analysis in space–time adaptive processing airborne radar[J]., 2013, 10(5): 1214-1218. doi: 10.1109/LGRS.2012.2236639.

[7] 马泽强, 王希勤, 刘一民, 等. 基于稀疏恢复的空时二维自适应处理技术研究现状[J]. 雷达学报, 2014, 3(2): 217-228. doi: 10.3724/SP.J.1300.2014.14002.

MA Zeqiang, WANG Xiqin, LIU Yimin,. An overview on sparse recovery-based STAP[J]., 2014, 3(2): 217-228. doi: 10.3724/SP.J.1300.2014.14002.

[8] BANG J H, MELVIN W L, and LANTERMAN A D. Model- based clutter cancellation based on enhanced knowledge- aided parametric covariance estimation[J]., 2015, 51(1): 154-166. doi: 10.1109/TAES.2014.130413.

[9] CARLSON B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]., 1988, 24(4): 397-401. doi: 10.1109/7.7181.

[10] VOROBYOV S A. Principles of minimum variance robust adaptive beamforming design[J]., 2013, 93(12): 3264-3277. doi: 10.1016/j.sigpro.2012.10.021.

[11] ABRAMOVICH Y I, JOHNSON B A, and SPENCER N K. Sample-deficient adaptive detection: adaptive scalar thresholding versus CFAR detector performance[J]., 2010, 46(1): 32-46. doi: 10.1109/TAES.2010.5417146.

[12] KANG B, MONGA V, and RANGASWAMY M. Rank- constrained maximum likelihood estimation of structured covariance matrices[J]., 2014, 50(1): 501-515. doi: 10.1109/TAES. 2013.120389.

[13] GERLACH K and PICCIOLO M L. Airborne/Spacebased radar STAP using a structured covariance matrix[J]., 2003, 39(1): 269-281. doi: 10.1109/TAES.2003.1188909.

[14] NEUMAIER A. Solving ill-conditioned and singular linear systems: a tutorial on regularization[J]., 1998, 40(3): 636-666. doi: 10.1137/S0036144597321909.

[15] HANSEN P C. Discrete Inverse Problems: Insight and Algorithms[M]. Philadelphia: SIAM Press, 2010: 95-97. doi: http://dx.doi.org/10.1137/1.9780898718836.

[16] 陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社, 2005: 267-269.

An Adaptive Estimation Method of Diagonal Loading Parameter for Airborne Radar

JIANG Lei WANG Tong

(,,710071,)

Diagonal loading method can be exploited to improve the performance of Space Time Adaptive Processing (STAP) in the face of limited training data. However, the diagonal loading level may be not easily determined in fact. To solve this problem, an adaptive parameter estimation method based on the received radar data is proposed. The diagonal loading problem is firstly transformed into the Tikhonov regularization problem. Then, Generalized Cross Validation (GCV) is introduced to construct the optimization problem. Finally, secant method is utilized to solve the optimization problem and calculate the loading parameter. The performance of the method is demonstrated using both simulated data and measured data. The results show that the method can improve the radar moving target detection performance in a limited sample support environment.

Target detection; Space Time Adaptive Processing (STAP); Diagonal loading; Parameter estimation; Generalized Cross Validation (GCV); Secant method

TN959.73

A

1009-5896(2016)07-1752-06

10.11999/JEIT151003

2015-09-08；改回日期：2016-05-03；网络出版：2016-06-03

王彤 twang@mail.xidian.edu.cn

国家自然科学基金(61372133)

The National Natural Science Foundation of China (61372133)

姜 磊： 男，1987年生，博士生，研究方向为阵列信号处理、空时自适应信号处理.

王 彤： 男，1974年生，教授，研究方向为机载雷达运动目标检测、合成孔径雷达成像.