基于Hilbert变换的单边带调制系统设计与实现

陆存波

（北京圣非凡电子系统技术开发有限公司北京100141）

基于Hilbert变换的单边带调制系统设计与实现

陆存波

（北京圣非凡电子系统技术开发有限公司北京100141）

为了解决基于希尔伯特变换的单边带调制系统中I/Q信号幅度不一致的问题，本文通过理论分析和公式推导的方法得出影响I/Q信号正交性的主要因素是滤波器的阶数，并通过试验分析了不同阶数的滤波器是如何影响I/Q信号的正交性的，得出了滤波器阶数要保证至少覆盖3.7个信号周期才能确保I/Q信号正交的结论。同时给出了在ADSP上实现希尔伯特滤波器的具体流程。此外，给出了基于AD9957的数字正交上变频的设计方法和实现流程。

单边带调制；希尔伯特变换；AD9957；ADSP

单边带调制是模拟调制方法里面性能相对非常优越的一种制式，具有占用带宽小、功耗低等优点［1］。由于滤波器设计的困难，使得单边带调制技术没有广泛应用于传统的通信系统中。但是随着软件无线电技术理论发展的成熟，以及DSP、FPGA，DDS等数字信号处理器的快速发展，使得单边带调制技术在数字信号处理平台上的实现变得简单可行［2］。

单边带调制方法包括滤波法与正交变换法两类。虽然滤波法在理论上容易实现，但由于数字滤波器占用系统资源巨大，在现实中难以实现。正交变换法由于是在基带上对数据进行希尔伯特变换处理，所以数据速率相对较低、运算量较小；基带信号的同相和正交分量与载波的同相和正交分量对应相乘再相加的过程运算量很大，但是是在DDS中完成，所以不占用DSP的系统资源。张敬利等人提出了一种插值-滤波法的单边带调制方法［3］，虽然符合DSP程序设计的特点，但是只能得到调制在固定频率的上下边带的信号。所以本文选用基于希尔伯特正交变换的方法实现单边带调制系统。针对目前单边带调制系统中普遍存在的I/Q信号不正交的问题，本文详细分析了滤波器阶数如何影响I/Q信号的正交性，并对基于窗函数法设计的希尔伯特滤波器产生的幅值误差对I/ Q信号的正交性的影响进行了分析，并通过试验定量分析了不同阶数的滤波器对I/Q信号正交性的影响，得出了滤波器阶数要保证至少覆盖3.7个信号周期才能确保I/Q信号正交的结论。在此基础上设计了希尔伯特滤波器，并在由ADSP21489和AD9957芯片为主组成的软件无线电平台上实现了单边带调制系统。

1　希尔伯特滤波器的设计与实现

1.1希尔伯特变换

希尔伯特变换是希尔伯特滤波器设计的基础，它可以提供的相位变化而不影响频谱分量的幅度。连续时间信号的Hilbert变换定义为：

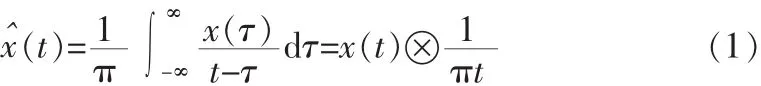
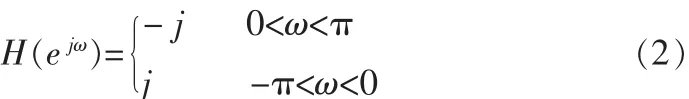
通过傅里叶逆变换可以得出：

所以，离散时间信号x（n）的Hilbert变换为：

信号x（n）经希尔伯特变换后，频谱不发生变化，相位连续，且与x（n）相互正交。

1.2希尔伯特滤波器的设计

希尔伯特滤波器在单边带调制系统中的位置如图1所示，它保证了I/Q信号的正交性，滤波器设计的好坏直接关系到整个系统设计的成败。

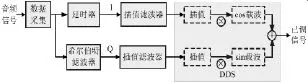
图1　单边带调制系统流程图

在实际系统设计中，经常会遇到I/Q信号幅度不一致的问题，有的文献［4］中采用将Q信号幅度乘以一个加权因子的方法使I/Q信号幅度近似一致，这种方法是错误的。因为对于不同幅度和频率的信号，加权因子的值是不同的，这在实际的系统设计中是无法实现的。I/Q信号的幅度不一致说明了两信号不正交，两信号不正交说明所做的希尔伯特变换是错误的，这通常是由于希尔伯特滤波器的阶数不够导致的。

理想的希尔伯特滤波器长度是无穷大，但基于窗函数法设计的FIR滤波器的长度是有限的，这必然会使输入输出信号的正交性受到影响。但在实际工程应用中，只要保证输入输出信号在误差允许范围内正交即可。因此，滤波器阶数的选择是关键，阶数太长，误差变小，但运算量变大，影响算法的实时性；阶数太小，运算量变小，但误差变大，影响输入输出信号的正交性。所以要在运算量和误差之间折衷处理，使选择的阶数既保证实时性又保证正交性。为了保证I/Q信号的正交性，要求I信号必须有（L-1）/2的群时延，其中L为Hilbert滤波器的长度。

以本系统的设计为例，信号的正交性用Q幅值误差表示，Q幅值误差越小，信号的正交性越好。设音频信号的采样速率为16k，那么对于300 Hz的信号，一个周期大约有53个点（16000÷300≈53.3）。如果希尔伯特滤波器的阶数为240，那么滤波器能够覆盖约4.52个周期的信号（241÷53.3≈4.52），Q信号幅值保持不变，如图2（a）所示，完全能够满足实际项目的需要；如果希尔伯特滤波器的阶数为26，那么滤波器能够覆盖大约0.5个周期的信号（27÷53.3≈0.5），Q信号幅值明显发生变化，如图2（b）所示，不满足正交性关系，虚线为I信号，实线为Q信号。虚线为I信号，实线为Q信号。图（a）中Q信号幅值与I信号保持一致，IQ信号正交；图（b）中Q信号幅值与I信号不一致，IQ信号不正交。

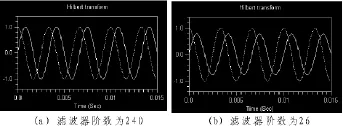
图2　滤波器阶数对Q信号幅值的影响

表1列出了滤波器阶数与正交性的关系，假设音频信号频率为300 Hz，I信号的幅值为1.0，理想的Q幅值也为1.0，Q幅值误差=（实测的Q幅值－理想的Q幅值）差的绝对值/理想的Q幅值。从表1可以看出，随着滤波器阶数的增加，滤波器能够覆盖的信号周期数越来越多，Q幅值误差越来越小，所以I/Q信号的正交特性越来越好，本系统中滤波器的阶数为240，已经完全能够满足正交性的指标要求。

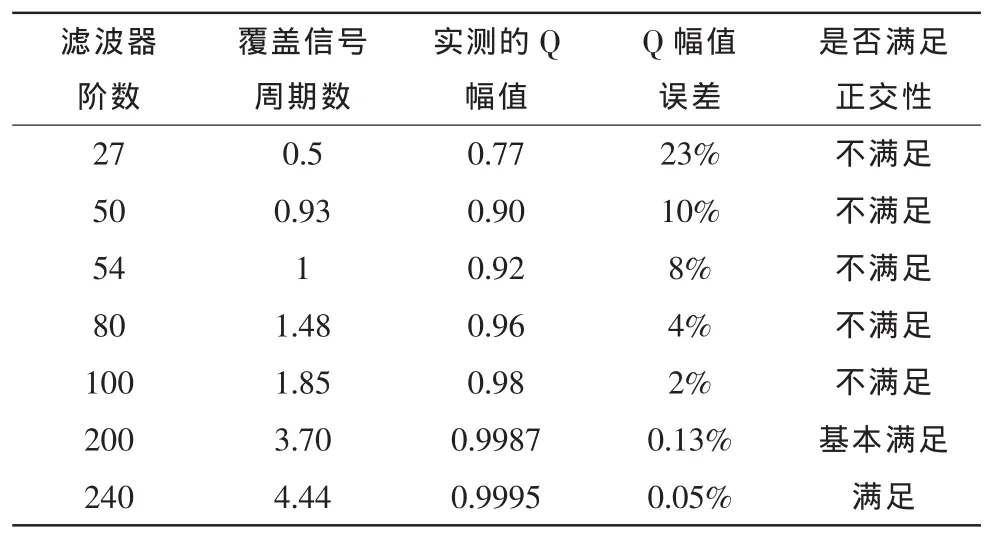
表1　滤波器阶数与Q幅值的关系

在希尔伯特滤波器的设计中，只要滤波器能够对最小频率的信号实现正交变换，就能保证对所有频率的信号实现正交变换，换言之，只要滤波器能够保证对最大波长的信号实现正交变换，就能保证对所有波长的信号实现正交变换，当然，前提是信号没有失真。假设滤波器阶数为270，采样频率为16 kHz，当信号频率从300 Hz提高到900 Hz时，滤波器能够覆盖的周期数从大约5.1增加到15.2，输入输出信号的正交性变得更好，所以只要对300 Hz的信号正交就能保证对所有大于300 Hz的信号正交。所以，在滤波器阶数和采样频率一定的情况下，信号频率越小，滤波器覆盖信号的周期数越小，正交性越差；信号频率越大，滤波器覆盖信号的周期数越大，正交性越好。而在滤波器阶数和信号频率一定的情况下，采样频率越小，滤波器覆盖信号的周期数越大，正交性越好；采样频率越大，覆盖信号的周期数越小，正交性越差。在希尔伯特滤波器阶数一定的情况下，滤波器覆盖信号周期数与信号频率和采样频率的关系如图3所示。

1.3Hilbert滤波器的DSP实现

本系统采用ADI公司的ADSP21489实现了希尔伯特滤波器，实现流程如图4所示。首先开辟运算缓冲区buffer，设置buffer的初值为0，长度为Hilbert滤波器长度L与DMA数据块长度N之和L+N；然后将DMA方式输入的N个数据放入缓冲区buffer的末尾；接着将Hilbert滤波器从缓冲区的首部滑动到尾部，每滑动一个数据，滤波器系数都与buffer中对应的数据做乘累加运算得到一个输出数据，最终得到N个输出数据，N个输出数据组成一个数据块通过DMA方式输出；最后将buffer中的所有数据左移N个位置，从而buffer中的前N个数据被移出，尾部为下一次DMA输入留出N个数据位置。由4节可知送入DDS的I/Q数据采样速率为fIQ，所以N个数据送入DDS中的时间为N/fIQ，所以希尔伯特变换的时间必须小于N/fIQ，本系统采用乒乓方式将I/Q数据连续送入DDS。希尔伯特滤波器的系数是用MATLAB的fdatool工具箱生成的。

图3　希尔伯特滤波器覆盖信号周期数与信号频率和采样频率的关系

图4　在DSP上实现Hilbert滤波的流程图

2　希尔伯特滤波器阶数对I/Q信号正交性的影响

理想的希尔伯特滤波器是非因果，滤波器阶数无穷大［5］，而实际的基于窗函数法设计的FIR滤波器的阶数是有限的，这必然会导致计算误差（Q幅值误差）的存在，这对基于正交变换的数字上变频系统会产生什么影响呢？以下进行分析和推导。本文以上边带调制为例，设载波频率为ω，调制信号频率为Ω，I信号为cos（Ω），理想的Q信号为sin（Ω），实测的Q信号为sin（Ω），则理想的基于正交变换的上边带信号cos（ω+Ω）产生方法为：基带和载波的同相分量和正交分量分别相乘之后再相加：

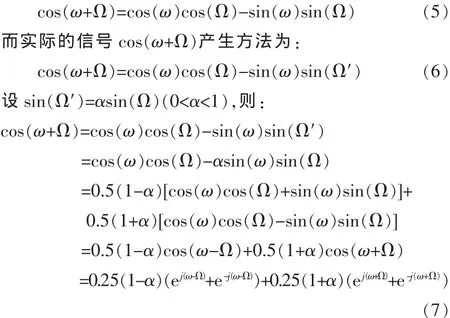
基于以上分析，在上边带调制中，希尔伯特变换幅度误差会在下边带位置产生误差频率ej（ω-Ω）和e-j（ω-Ω），其中e-j（ω-Ω）为负频率，同时原始频率的幅度变为原来的0.5（1+α）倍。如图5所示，（a）为I/Q信号幅值相等时的上边带信号，（b）为Q信号幅值变为原来的0.7倍时的情况，在下边带位置产生一个误差信号，误差信号幅度为理想信号幅度的15%，由表1可知，I/Q信号不满足正交性。由表1，当滤波器阶数为200时，Q信号幅值变为理想信号的99.87%，误差信号幅度变为理想信号的0.13%，基本可以忽略不计。

综上所述，有限长的滤波器导致了Q幅值误差的存在，由于误差的存在产生了新的频率，从而影响了I/Q信号的正交性。

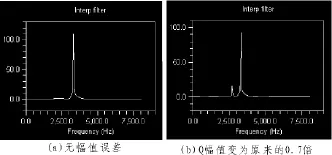
图5　Q幅值误差对频率的影响

3　插值滤波器

由于基带信号的速率低于DDS要求的输入信号的速率，所以需要对基带信号进行插值使得插值后的数据速率与DDS要求的输入数据的速率完全一致。以本系统的设计为例，DDS要求的输入数据速率为768 kHz，基带信号的采样频率为16 kHz，因此插值的倍数为48倍（768 kHz/16 k）。48倍插值滤波器的阶数为384，采用MATLAB的interp函数生成。在DSP平台上设计实现了48倍插值滤波器，插值滤波器的实现方法与1.3中希尔伯特滤波器的实现方法相同。这里的插值滤波器指的是图1中的“插值滤波器”，而非DDS中的“插值”滤波器。

4　基于AD9957　的数字正交上变频

AD9957［6］是一款数字正交上变频器，用于产生载波信号，载波以正交形式施加到I和Q乘法器并相加，从而产生代表正交调制载波的数据流。载波信号的频率是由直接数字频率合成器（DDS）来控制的，DDS可以利用内部参考时钟（SYSCLK）非常精准地产生所需的载波频率。载波的采样速率等于内部系统时钟频率fSYSCLK。数字正交上变频系统设计的关键是数据速率的匹配，即数据的采样速率与载波信号的采样速率一致。对于Blackfin接口（BFI）模式，fPDCLK为I和Q数据流的位速率，且fPDCLK=fSYSCLK/R，其中R为DDS中可编程插值滤波器的插值因子，可以实现2倍至63倍范围内的插值。由于每个I和Q字均具有16位分辨率，所以送入DDS的I/ Q数据采样速率fIQ=fPDCLK//16。设AD的采样速率为fAD，图1中“插值滤波器”的插值倍数为R′，则fIQ=fAD×R′。所以，基带数据与载波信号的速率匹配公式为：

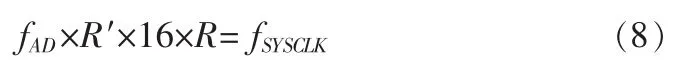
本系统中fAD=16 ksps，R′=48，R=32，fSYSCLK=393.216 Msps。通过以上分析和计算，就能保证基带数据的采样速率与载波的相同，只要IQ信号以该速率送给DDS就能正确实现数字上变频。

5　结束语

文中介绍了基于希尔伯特变换的单边带调制系统的设计实现方法。详细分析了希尔伯特滤波器的设计方法，介绍了在DSP平台上实现希尔伯特变换的具体流程；分析解决了上变频过程中数据采样速率的匹配问题，将基带的正交I/Q数据流按照预先计算好的速率送入DDS就可以完成数字上变频。本方法具有较好的工程参考价值。

［1］樊昌信．通信原理［M］．北京：国防工业出版社，2006．

［2］杨小牛，楼才义．软件无线电技术与应用［M］.北京：北京理工大学出版社，2010．

［3］张敬利，丁国栋，易克初．基于DSP的信号单边带调制的实现［J］．通信技术，2003（3）:30-31．

［4］蒋春峰．基于Hilbert变换的单边带调制的实现［D］．武汉：华中科技大学硕士

［5］赵树杰，史林．数字信号处理［M］．西安：西安电子科技大学出版社，1997．

［6］ANALOG DEVICE．AD9957［R］．Norwood:DataSheet．Analog Device Inc，2000:1-60．

Based on Hilbert transformation single sideband modulation system design and realization

LU Cun-bo
（Beijing Shengfeifan Limited Company of Eletronic System and Technological Development，Beijing 100141，China）

In order to resolve the non-quadrature of the I/Q signals in the single side band（SSB）modulation system which is based on the hilbert transform，based on the method of theoretical analysis and formula derivation the paper present that the main factor affecting the orthogonality of I/Q signal is the order of the filter，and analysis how the filter of different order affects the orthogonality of I/Q signal by means of experiments，It comes to conclusion that the filter order must be guaranteed at least 3.7 signal cycles to ensure that the I/Q signal is orthogonal.Meanwhile provides the flow of hilbert filter which is implemented on the ADSP.In addition，the paper presents the design method and realization process of the digital orthogonal upper frequency conversion based on AD9957.

SSB；Hilbert transform；AD9957；ADSP

TN99

A

1674－6236（2016）12-0138-03

2015-07-03稿件编号：201507031

陆存波（1982—），男，吉林长岭人，硕士，工程师。研究方向：数字信号处理、DSP设计。