基于CS的无线传感器网络动态分簇数据收集算法

张　策　张　霞　李　鸥　王　冲　张大龙

(中国人民解放军信息工程大学信息系统工程学院　郑州　450001)



基于CS的无线传感器网络动态分簇数据收集算法

张策张霞李鸥王冲张大龙

(中国人民解放军信息工程大学信息系统工程学院郑州450001)

(cezhang@foxmail.com)

降低能耗、实现网络的能量均衡和延长网络寿命，是设计无线传感器网络(wireless sensor networks, WSNs)数据收集算法所面临的主要挑战之一.针对现有无线传感器网络分簇数据收集算法不考虑网络中事件源的发生对数据空间相关性的影响的情况，提出了一种基于压缩感知的以事件源为中心的动态分簇(CS-based dynamic clustering centred on event source, CS-DCES)算法.该算法利用欧氏距离空间相关性模型和第一联合稀疏模型，将受同一个事件源影响的节点分在一个簇中，并以簇为单位进行数据重构，以此增加簇内节点感知数据的空间相关性，减小每簇数据观测量；利用压缩感知收集数据，计算事件源位置，根据事件源位置变化实行动态分簇.并通过实验分析了影响该算法性能的3个因素，即事件的衰减系数、事件源之间的距离和事件源个数，最后给出了算法的适用条件.仿真分析表明，相对于已有算法，CS-DCES在满足同一重构精度的前提下，有效减小了数据传输量，节省网络能耗，延长网络寿命.

无线传感器网络；数据收集；事件源；空间相关性；动态分簇

无线传感器网络(wireless sensor networks, WSNs)广泛应用于医疗救护空间探索、军事应用、智能家居和环境监测等领域，被看作连接人类社会与物理世界的纽带.传感器节点通常依靠电池供电，能量受限，因此降低能耗、延长网络寿命是WSNs数据收集方法研究的一大挑战.

WSNs中节点布设密度大，节点感知到的数据存在大量冗余信息，且受环境影响十分大.传统的数据收集方法是通过多跳中继的方式将节点采集到的信息传送给汇聚节点(Sink)，这种方法会收集到大量冗余信息，且越靠近Sink的节点需要转发消息的次数越多、耗能越快，在Sink周围易形成能量空洞，使整个网络瘫痪.

近年来，压缩感知理论(compression sensing, CS)[1-3]给信息处理领域带来了革命性的突破，它指出将可压缩高维信号投影到某个特定低维空间上，通过数值最优化问题从这些少量投影中准确重构出原始信号.文献[4]将CS理论应用在单跳的WSNs，实现了对数据的压缩;文献[5-6]将压缩感知理论应用于大规模多跳WSNs中，有效减少网内数据的传输能量损耗，且保持了网内能量均衡.压缩感知理论在WSNs中数据收集的成功应用，解决了网络能量消耗不均衡问题，且具有压缩过程简单而数据重构过程复杂的特点，适合传感器节点信息处理能力不足和能源受限的特点.文献[7]针对WSNs分布式数据收集特点，首次提出分布式压缩感知理论(distributed compressed sensing, DCS)，实现了在WSNs中对多信号的压缩感知编码.文献[8]将CS技术与Pegasis路由协议相结合，构建路由链，在链中压缩数据以改善网络寿命，在Sink处统一重构数据，与树形路由中最小生成树相比，虽然链路路由中节点之间每一跳能耗最小，但整个链路能耗不一定达到最小，且网络鲁棒性差.文献[5,9]将CS技术与树形路由协议相结合，以获得高效的压缩数据，但是简单地在树形路由中使用CS，会增加叶节点和距离叶节点较近的中间节点的通信量，而网络的吞吐量并没有提升.文献[10]针对该问题提出了混合压缩感知(Hybrid-CS)数据收集方法，在树形路由中仅仅对一部分通信量高的父节点使用压缩感知技术，以此减少网络数据通信量.

以上研究针对平面网络结构，当网络规模较大时，通过分簇构建层次化网络结构，更有助于提高网络数据传输和管理的效率.文献[11]借鉴Leach的思想，研究适合于分簇结构的压缩感知数据收集，建立模型计算出全网最优簇首个数，随机选取簇首，并使得簇首均匀分布在网络中，Sink得到每个簇收集到的数据后统一重构.以上文献均没考虑节点感知数据之间的相关性问题和事件源对数据相关性的影响，在WSNs中会有一些人们感兴趣的事件源发生，如温度监测场景中的着火点，影响着局部采集数据之间的空间相关性.文献[12-15]分析了WSNs网络性能受空间相关性的影响很大.文献[16]分析了网络中影响源对数据相关性的影响，簇内的全局影响因子会使得簇中的共有稀疏度增加而特有稀疏度减小，总的稀疏度和观测数量M减小，通过空间相关性和最优距离对网内节点分簇，在Sink端统一重构，但是文中没有确切地给出影响源的位置和影响范围.

为此本文提出一种基于压缩感知的以事件源为中心的动态分簇(compressive sensing based dynamic clustering centered on event source, CS-DCES)算法，考虑网络中事件源的发生对数据相关性的影响，以事件源为中心进行分簇，每个簇内收集到的数据单独进行数据重构;在数据收集过程中计算事件源方位，根据事件源方位变化动态分簇，以实现高精度、低能耗的数据收集.

1　系统模型

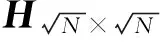
(1)

(2)

WSNs中，每个传感器节点采集的信号强度是由网络中S个事件源的信号叠加而成的，即[17]

XN×1=ΨN×NVN×1=

(3)

其中Ψ为传感器感知数据随距离衰减系数矩阵.本文利用欧氏距离的空间相关性模型.假定传感器节点i和j的坐标为(xi,yi)和(xj,yj)，2节点之间的距离为

(4)

若在节点i处有事件源发生，节点i接收到信号功率为Pi，节点j接收到信号功率为Pj，信号按欧氏距离衰减，则有

(5)

其中,C为常数，n为信号的衰减系数.不同类型的事件源衰减系数不同.2个区域中节点采集到的信息之间的相关性与其欧氏距离成反比，距离越近、衰减系数n越小，节点采集到的信息越接近，相关性越大.本文令：

(6)

使用压缩感知技术进行数据收集，假设随机观测矩阵为Φ=(φi j)M×N，其中M≪N，使用文献[7]中给出的测量矩阵：

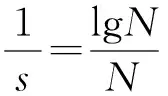
(8)

一般地，由于网络中事件源发生个数S≪N，向量V是稀疏的.通过此模型，可以将计算事件源方位向量V问题转化为已知Y求V的问题.根据文献[17]，式(8)符合压缩感知理论的观测模型，可将计算过程转化为一个求解凸优化问题：

(9)

2　基于相关性模型的分簇方法

在大规模WSNs中，节点感知到的数据之间存在着空间上的相关性.本文利用第一联合稀疏模型(joint sparsity model-1, JSM-1)[18]对WSNs中节点采集到的信息进行建模分析.

在JSM-1中，假设网络中有N0个节点，节点j采集数据xj可以分为共有数据部分zc和特有数据部分zj，即：

(10)

共有数据与特有数据在同一个稀疏基Ψ下稀疏表示为：

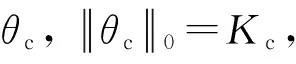
(11)

(12)

其中,共有数据的稀疏度为Kc，特有数据zj的稀疏度为Kj.根据压缩感知理论要求，为了保证在数据重构时的精度，观测次数M满足：

(13)

(14)

传统的压缩感知数据收集方法中，将所有传感器节点采集的信息统一进行重构.然而由于网络环境复杂，往往有多个分布于不同区域的事件，影响传感器节点采集的数据，这些事件之间是彼此独立的.例如，在室外温度测量场景，全局影响因子如日照、风等，影响共有数据部分zc；局部影响因子如水流、动物和着火点等，影响特有数据部分zj.在这种情况下，全网节点统一进行处理的将使得Kc较小而Kj较大，总的稀疏度K增大，从而使得观测次数M增高.

网络中的事件源会成为影响其周边节点感知数据的主要因素，且节点离事件源越近，受影响程度将越大.因此本文提出以事件源为中心分簇.假设簇内共有N1个节点，若随机分簇，以簇为单位进行数据重构，则簇内总稀疏度Kintra为：

(15)

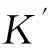
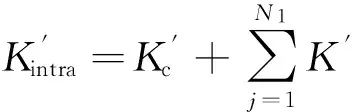
(16)

3　动态分簇数据收集算法

针对有感兴趣的事件源发生的WSNs，本文根据以上2种模型，提出了基于压缩感知的动态分簇数据收集算法.整个算法流程如图1所示：

Fig. 1　CS-DCES algorithm flow chart.图1　CS-DCES算法流程图

算法具体过程如下：

1) 获取事件源方位.假设网络中有事件源发生，且Sink已经得到了全网节点采集到的数据Xtot，此数据可以通过非压缩感知算法或者压缩感知算法方式获得.由系统模型中式(3)可知，事件源方位向量Vtot为

(17)

2) 以事件源为中心分簇.根据相关性模型，Sink获取事件源方位后，通知距离每个事件源位置最近的传感器节点，将其确定为簇首；若同时有多个节点与事件源距离相等且最近，则Sink在这些节点中随机选出1个节点作为本簇簇首，此时一定会选出1个簇首，即分簇收敛.由簇首广播其簇首信息，其余节点选择距离自己最近的簇首，加入该簇.Sink为每个簇首分配不同的随机种子ξ，簇首接收随机种子ξ后与本簇内成员节点IDj组合生成随机种子(ξ,IDj)，利用该种子随机生成M维的观测矩阵Φ′.图2为网络中有3个事件源时的分簇情况.

Fig. 2　Network clustering diagram.图2　网络分簇示意图

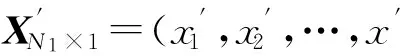
算法1. 在有N1个成员节点的簇中，簇首在第t轮第i个测量值的收集算法.

②fori=1toM

④ end for

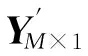
⑥ end if

4) 数据重构.Sink收到S个簇首发送的观测向

算法2. Sink重构第i个簇内的数据.

① if Sink 收到簇首观测向量Yithen

②fori=1toS

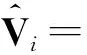
ΦiΨiVi;

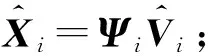
⑤ end for

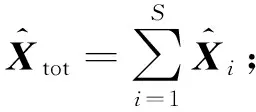
⑧ end if

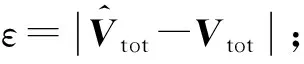
⑩ ifε>ζthen

6) 簇首轮换.若经Sink判断，网络中事件源方位没有发生变化，为了使簇中能耗均衡，1次数据收集后，保持各个簇的规模和位置不变，在簇内实行簇首轮换.各个簇内的成员节点将自身剩余能量信息发送至簇首，由簇首判断选取簇内剩余能量最大的节点作为下一轮数据收集的簇首，并将新簇首信息发送给簇内其余成员节点进行簇首轮换，以防止簇内能量消耗不均衡造成网络过早瘫痪.

4　仿真与分析

为了验证CS-DCES算法的有效性，本文在MATLAB平台下进行算法仿真分析，仿真环境设置如下：全网有400个传感器节点均匀分布在20×20的区域中，网络中有S个事件源发生.Sink在网络中的坐标为(10,50)并有固定的能源供应，假设网络中普通节点的初始能量值为0.05，一旦其能量小于0时，即认为该节点死亡停止工作，本文采用正交匹配追踪算法(orthogonalmatchingpursuit,OMP)作为重构算法.

在WSNs中，大部分基于压缩感知的数据收集算法较少考虑采集数据由于受不同事件源影响导致空间相关性改变，而把网络中所有节点采集的数据看作1个信号并在Sink处统一重构，例如文献[11],为了便于描述，本文将该类算法记为CS-URA(unifiedrestructuringalgorithm)算法.文献[16]中的SC-CDG算法考虑了网络中事件源对数据相关性的影响，却没有确切地给出影响源的位置和影响范围，本文拟与CS-URA算法和SC-CDG算法进行比较，比较3种算法在重构数据信噪比和网络寿命上的性能优劣.仿真结果为1 000次仿真之后的平均值.

整个网络中的能量消耗，主要是节点与簇首、簇首与Sink之间的无线通信能耗.本文采用文献[11]给出的能量消耗模型，即

ETx(L,d)=Eelec×L+εamp×L×d2,

ERx(L)=Eelec×L,

其中，ETx(L,d)表示数据发送节点将1个L位的数据传输d时所消耗的能量，ERx(L)表示数据接收节点接收L位数据消耗的能量，Eelec表示节点发送或接收单位位所消耗的能量，εamp表示节点功率放大系数.

4.1算法性能比较

如图3所示给出了重构信噪比SNR和观测次数M的关系.仿真假设网络中有2个事件源发生，其位置为(15,5)和(5,15)，衰减系数n=4.由图3可知，随着观测次数M的增加，信噪比提高，且只需较小的观测次数就能达到较高的重构精度；当M持续增大，信噪比趋于平稳，重构精度达到最优，M的持续增大并不会带来更高的重构精度，反而会增加网络的能耗开销.当信噪比SNR=27 dB时，CS-URA算法观测次数M=33，SC-CDG算法观测次数M=32，而CS-DCES算法的观测次数为M=13，减少了60%左右.由于CS-DCES算法以事件源为中心，将空间相关性高的节点分在一个簇中，与其他2种算法相比使得簇内总的稀疏度降低，当以簇为单位重构数据时，可以以较小的观测次数M达到同样的精度.

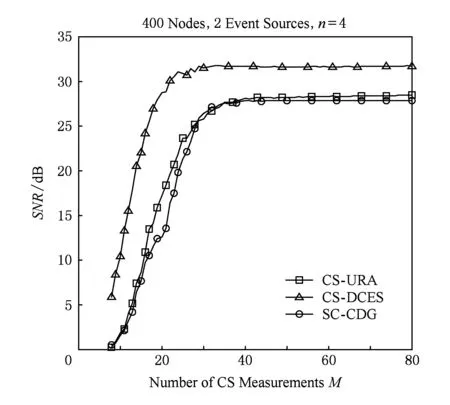
Fig. 3　The relationship between reconstruction SNR 　　　and the number of measurements.图3　重构信噪比与观测次数关系

图4反映了当数据包长度为1 B、信噪比SNR=27 dB时数据收集轮数r与死亡节点数的关系图.由仿真结果可得，CS-URA算法在收集445轮时第1个节点死亡，收集674轮时所有节点死亡；SC-CDG算法在收集632轮时第1个节点死亡，收集641轮时所有节点死亡；CS-DCES算法收集1892轮时第1个节点死亡，收集2 164轮时所有节点死亡.相比之下，网络寿命增加了221%和237%，有效延长了网络寿命，且由于本方法使用了簇首轮换机制，使得整个网内能耗得到了均衡.

Fig. 4　Network lifetime.图4　网络寿命

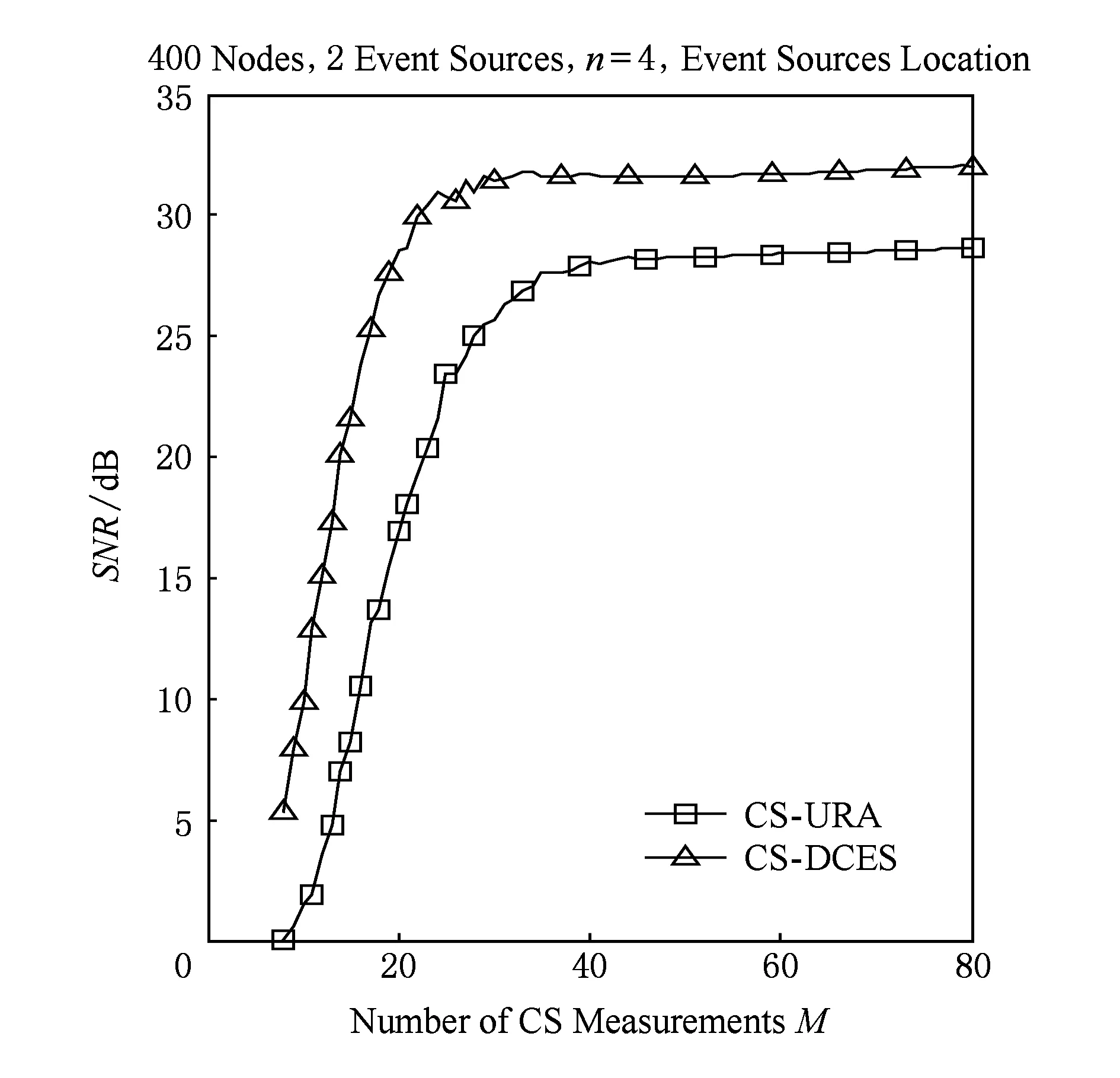
Fig. 5　Reconstruction of event source position.图5　事件源位置重构

4.2定位事件源

在CS-DCES算法中，事件源位置的确定直接决定了算法的有效性.在本文所建立的模型下，CS-DCES与CS-URA均能重构出事件源位置，CS-DCES算法在相同重构精度时所需观测次数更少，其性能如图5所示.CS-DCES算法重构事件源方位如图6所示.由图6可知CS-DCES算法可以精确重构出事件源位置，以判断事件源位置是否发生变化，为本算法的有效性提供了条件.

Fig. 6　Event source distribution map.图6　事件源分布图

4.3影响算法性能因素分析

CS-DCES算法是以事件源为中心对全网节点进行分簇，所以事件的衰减系数n、事件源之间的距离d和事件源个数S都会影响CS-DCES的性能，下面通过仿真讨论上述因素对算法性能的影响.

图7是衰减系数n与SNR的关系.2个事件源位置为(1,1)和(20,20)，相距d=26.87.当衰减系数分别为2.5，3，3.5，4，6，8时，较小的观测次数M就能达到较高的SNR;当衰减系数n=2时，即事件源的影响范围扩大，SNR最高只有15，重构精度变低，此时CS-DCES算法就不再适用.进一步仿真了n=2时CS-URA算法的性能，并与CS-DCES算法进行了对比，结果如图8所示.

Fig. 7　Impact of attenuation coefficient on performance.图7　衰减系数对性能影响

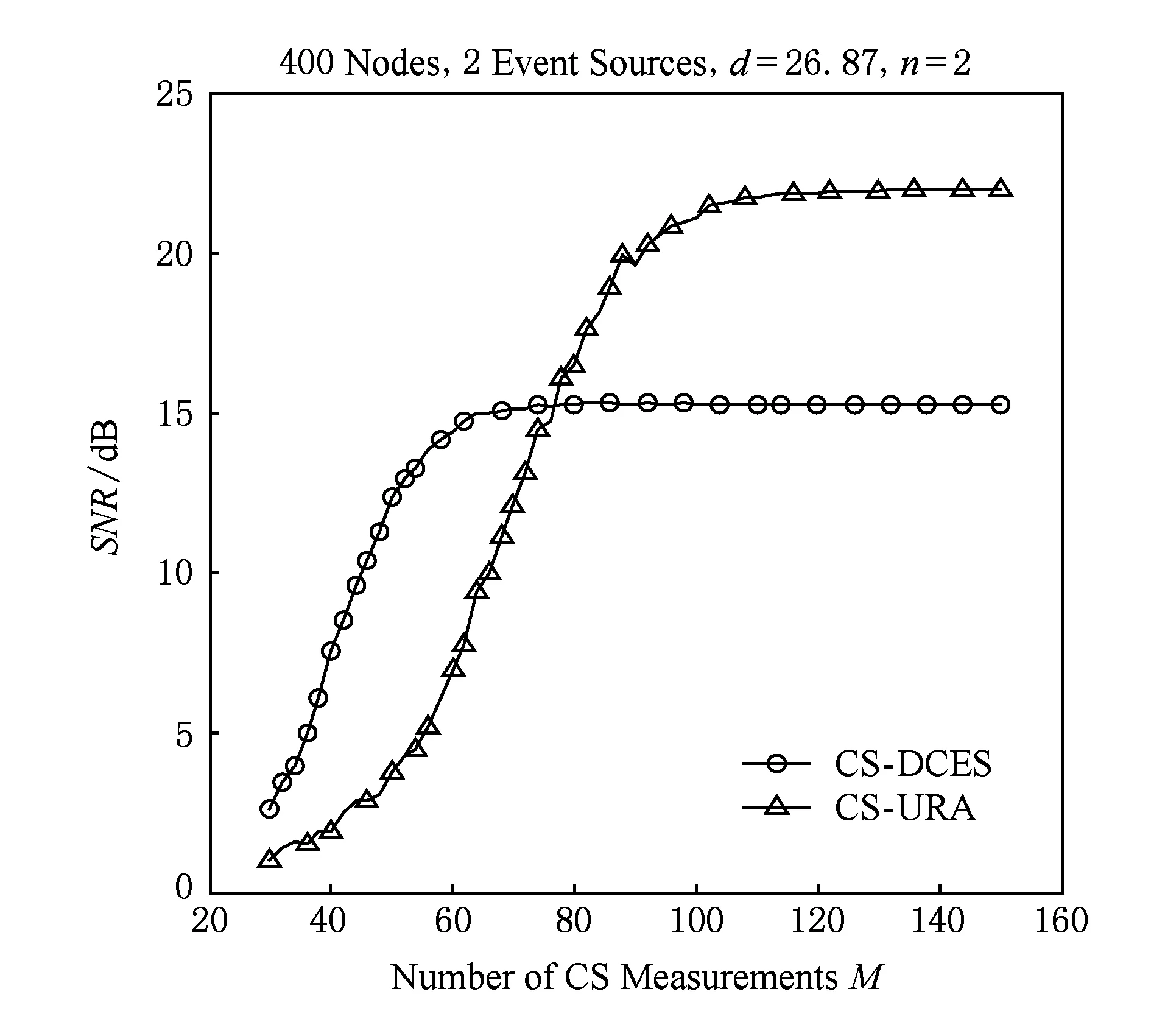
Fig. 8　Comparison of CS-DCES and CS-URA. 图8　CS-DCES算法与CS-URA算法性能对比

M<76时,CS-URA算法的精度没有CS-DCES算法的高；M>76时，CS-URA算法却能达到较高精度.由于CS-DCES算法根据节点与事件源的距离，将主要受同一个事件源影响的节点分在一个簇中.当n减小，会使得位于2个事件源之间、同时受到这2个事件源影响的节点受影响的程度增大，且使2种影响程度差距变小.这样在每个簇单独重构时，簇中一部分节点采集到的数据主要受本簇中事件源的影响，另一部分节点采集到的数据同时受2个事件源的影响，此时CS-DCES算法中簇内总稀疏度K并不会减小甚至增大，重构误差变大，性能变差.

图9反映了网络中有2个事件源时，事件源距离d对CS-DCES算法性能的影响.圆形曲线表示2个事件源位于(3,3)和(18,18)时算法性能，三角曲线表示2个事件源位于(7,5)，(13,19)时算法性能，方形曲线表示2个事件源位于(10,9)，(9,15)时算法性能.由图9可知,事件源之间距离越大，SNR越高.当事件源之间的距离很小时，重构精度会很差，此时CS-DCES算法将不再具有优越性能.事件源距离的增大，削弱了簇与簇之间的相互影响，使得簇内的数据相关性主要受本簇内事件源的影响，从而降低簇中数据的稀疏度，减小观测次数.

Fig. 9　Impact of event source distance on performance.图9　事件源距离对性能影响

图10为事件源个数S对CS-DCES算法性能的影响.衰减系数n=4，使得事件源均匀地分布在网络中，正方形曲线表示事件源位于(5,15)，(15,5)时的算法性能，三角形曲线表示事件源位于(3,3)，(18,18)，(15，9)时的算法性能，圆形曲线表示事件源位于(5,5)，(5,15)，(15,5)，(15,15)时的算法性能.由仿真图可知，事件源个数越少且相距越远时，CS-DCES算法的性能越好.事件源个数的增多使得事件源之间距离减小的概率增加，在衰减系数一定的情况下，簇与簇之间的影响有可能会增大，算法性能就会受到影响;若事件源个数增多但彼此之间相距较远，则本算法性能同样不会变差.

由以上仿真结果可以得出，当WSNs中事件源的衰减系数小、距离大、个数少时，CS-DCES算法能保证收集数据重构精度的同时减少数据收集的能耗，延长网络寿命，性能优势明显.

Fig. 10　Impact of number of event sources on performance.图10　事件源个数对性能影响

5　总结和展望

本文针对有事件源发生的WSNs数据收集提出了CS-DCES算法，以此来增加簇内数据相关性，使得数据共有稀疏度增加而特有稀疏度减小，总的稀疏度减小，减小簇内观测次数.并根据事件源的位置变化调整分簇策略，实现动态分簇.通过仿真实验分析了算法性能，结果表明，本算法在同一重构精度前提下有效减小了数据传输量、节省网络能耗、延长网络寿命;讨论了衰减系数、事件源距离和事件源个数对算法性能的影响，算法在衰减系数大、事件源相距远和事件源个数少时，CS-DCES算法的重构精度更高、网络寿命更长，更具有优势.

在实际WSNs应用场景中均匀规则布设节点一般很难实现，且网络链路并非完全可靠.为了能将此模型算法运用到实际的工程中去，对随机布设节点的系统模型和算法实现的研究很有必要，WSNs在不可靠链路条件下运用压缩感知技术也将在后续研究工作中进行讨论.

[1]Donoho D L. Compressed sensing [J]. IEEE Trans on Information Theory, 2006, 52(4): 1289-1306[2]Baraniuk R. Compressive sensing [J]. IEEE Signal Processing Magazine, 2007, 56(4): 4-5[3]Candes E J, Wakin M B. An introduction to compressive sampling [J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30[4]Rabbat M, Haupt J, Singh A, et al. Decentralized compression and predistribution via randomized gossiping [C]Proc of the 5th Int Conf on Information Processing in Sensor Networks. New York: ACM, 2006: 51-59[5]Luo C, Wu F, Sun J, et al. Compressive data gathering for large-scale wireless sensor networks [C]Proc of the 15th Annual Int Conf on Mobile Computing and Networking. New York: ACM, 2009: 145-156[6]Wang J, Tang S, Yin B, et al. Data gathering in wireless sensor networks through intelligent compressive sensing [C]Proc of IEEE INFOCOM 2012. Piscataway, NJ: IEEE, 2012: 603-611[7]Wang W, Garofalakis M, Ramchandran K. Distributed sparse random projections for refinable approximation. [C]Proc of the 6th Int Conf on Information Processing in Sensor Networks. New York: ACM, 2007: 331-339[8]Osamy W, Salim A, Aziz A. Efficient compressive sensing based technique for routing in wireless sensor networks [J]. INFOCOMP Journal of Computer Science, 2013, 12(1): 1-9[9]Luo C, Wu F, Sun J, et al. Efficient measurement generation and pervasive sparsity for compressive data gathering [J]. IEEE Trans on Wireless Communications, 2010, 9(12): 3728-3738[10]Luo J, Xiang L, Rosenberg C. Does compressed sensing improve the throughput of wireless sensor networks? [C]Proc of IEEE Int Conf on Communications (ICC 2010). New York: IEEE Communications Society, 2010: 1-6[11]Wu X, Xiong Y, Huang W, et al. An efficient compressive data gathering routing scheme for large-scale wireless sensor networks [J]. Computers & Electrical Engineering, 2013, 39(6): 1935-1946[12]Pattem S, Krishnamachari B, Govindan R. The impact of spatial correlation on routing with compression in wireless sensor networks [J]. ACM Trans on Sensor Networks, 2008, 4(4): 24-31[13]Villas L A, Boukerche A, Oliveira H A B F D, et al. A spatial correlation aware algorithm to perform efficient data collection in wireless sensor networks [J]. Ad Hoc Networks, 2014, 12(1): 69-85[14]Gupta G, Misra M, Garg K. Energy efficient data gathering using prediction-based filtering in wireless sensor networks [J]. International Journal of Information and Communication Technology, 2013, 5(1): 75-94[15]Villas L A, Boukerche A, Guidoni D L, et al. An energy-aware spatio-temporal correlation mechanism to perform efficient data collection in wireless sensor networks [J]. Computer Communications, 2013, 36(9): 1054-1066

[16]Wang Chong. Research on data gathering based on compressive sensing in wireless sensor networks [D]. Zhengzhou: PLA Information Engineering University, 2015: 37-44 (in Chinese)(王冲. 基于压缩感知的无线传感网数据收集技术研究[D]. 郑州: 中国人民解放军信息工程大学, 2015: 37-44)[17]Tang Liang, Zhou Zheng, Shi Lei, et al. Source detection in wireless sensor network by LEACH and compressive sensing [J]. Journal of Beijing University of Posts & Telecommunications, 2011, 34(3): 8-11 (in Chinese)(唐亮, 周正, 石磊, 等. 基于LEACH和压缩感知的无线传感网目标探测 [J]. 北京邮电大学学报, 2011, 34(3): 8-11)[18]Duarte M F, Sarvotham S, Wakin M B, et al. Joint sparsity models for distributed compressed sensing[C]Proc of the Workshop on Signal Processing with Adaptative Sparse Structured Representations. Piscataway, NJ: IEEE, 2005: 2729-2732

Zhang Ce, born in 1991. Master candidate. His main research interests include wireless sensor networks, routing protocol, and communication technology.

Zhang Xia, born in 1979. PhD and lecturer. Her main research interests include computer network, wireless sensor networks, and information operations (zhangxiaatzz@sina.com).

Li Ou, born in 1961. Professor and PhD supervisor. His main research interests include wireless sensor networks, cognitive radio networks, and Ad-hoc networks (zzliou@126.com).

Wang Chong, born in 1989. Master candidate. His main research interests include wireless sensor networks, routing protocol, and communication technology (wc38022122@126.com).

Zhang Dalong, born in 1976. PhD and lecturer. His main research interests include wireless sensor networks, MAC protocol, and communication technology (ttengzhang@163.com).

Data Gathering Using Dynamic Clustering Based on WSNs Compressive Sensing Algorithm

Zhang Ce, Zhang Xia, Li Ou, Wang Chong, and Zhang Dalong

(SchoolofInformationSystemsEngineering,PLAInformationEngineeringUniversity,Zhengzhou450001)

One of the major challenges of designing wireless sensor networks data gathering algorithm is to reduce energy consumption, achieve better balanced consumption and prolong the lifetime of sensor network. For the current clustering algorithms of data gathering in wireless sensor networks neglecting the impact of event sources on data spatial correlation, a CS-based dynamic clustering algorithm centred on event source (CS-DCES) is proposed in this paper. Utilizing the model of Euclidean distance spatial correlation and joint sparsity model-1, the nodes that affected by the same event source are clustered together and reconstruct those nodes readings within cluster in order to increase the spatial correlation of data and reduce the number of each cluster measurement. The algorithm exploits the compressive data to calculate the location of event source and clusters dynamically. Moreover, according to simulation, we analyze the three factors that influence the algorithm performance, and they are attenuation coefficient of event sources, distance between event sources and the number of event sources, and finally the application condition of CS-DCES is given. The simulations show that CS-DCES outperforms the existing data gathering algorithms in decreasing communication cost, saving the network energy consumption and extending the network survival time under the same accuracy.

wireless sensor networks(WSNs); data gather; event source; spatial correlation; dynamic clustering

2015-06-09；

2015-09-16

国家科技重大专项基金项目(2014zx03006003)

TP393

This work was supported by National Science and Technology Major Projects (2014zx03006003).