一种不完备混合数据集成聚类算法

史倩玉　梁吉业　赵兴旺

(山西大学计算机与信息技术学院　太原　030006)(计算智能与中文信息处理教育部重点实验室(山西大学)　太原　030006)



一种不完备混合数据集成聚类算法

史倩玉梁吉业赵兴旺

(山西大学计算机与信息技术学院太原030006)(计算智能与中文信息处理教育部重点实验室(山西大学)太原030006)

(ljy@sxu.edu.cn)

集成聚类技术由于具有较好的泛化能力，目前引起了研究者的高度关注.已有研究主要关注数值型完备数据的集成聚类问题.然而，实际应用中面临的数据往往是兼具数值属性和分类属性共同描述的混合型数据，而且通常带有缺失值.为此，针对不完备混合数据提出了一种集成聚类算法，首先利用3种缺失值填充方法对不完备混合数据进行完备化处理；其次在3种填充后的不同完备数据集上分别多次执行K-Prototypes算法产生基聚类结果；最后对基聚类结果进行集成.在UCI真实数据集上与传统聚类算法通过实验进行了比较分析，实验结果表明提出的算法是有效的.

集成聚类；不完备数据；混合数据；缺失值填充；K原型聚类算法

聚类分析是针对给定的数据集，根据元素之间的相似性度量自动将相似的元素划分到同一组，使得组内的元素相似性达到最大而组间元素的相似性达到最小的过程.目前，聚类分析技术已经在生物信息学、社会网络、图像处理等领域得到了广泛的应用[1].

目前，研究者针对不同应用领域已经提出了许多聚类算法[2-3]，但是已有算法存在一定的局限性.例如，针对同一数据集算法在不同参数设置下会得到不同的聚类结果，或者是传统的聚类算法在复杂结构的数据集上很难得到有效的聚类结果.

针对这些问题，研究者提出了聚类集成的方法[4-6].聚类集成的宗旨是合并某个数据集的多重“基聚类”结果，将其转化成统一的、综合的最终聚类结果，其主要包括3个阶段：生成基聚类、获取集成关系和确定最终聚类[7].例如，文献[4]介绍的CSPA算法是基于共协关系矩阵生成一个无向带权图，然后利用METIS算法对图进行分割从而得到最终的一致性聚类结果.Fred等人在文献[5]中提出的EAC算法同样基于共协关系矩阵，将该矩阵作为层次聚类算法的输入得到最终聚类结果.文献[6]构造了一个对象和类的加权二部图，运用谱聚类划分该图确定最终聚类.然而，现有的方法主要针对数值型属性或分类型属性单一类型的完备数据进行集成聚类.近年来，针对完备混合型数据的集成聚类问题，国内外学者已经开展了一些探索性的工作[8-10].文献[8]提出的混合数据集成方法首先分别对数值型属性和分类型属性部分进行聚类，然后将以上聚类结果看成是分类型数据，在其上应用分类型数据聚类算法来进行聚类集成并得到最终聚类结果.为了避免直接计算混合型数据间相似性的难题，文献[10]利用聚类集成技术产生混合数据间的相似性矩阵，最后基于此矩阵应用谱聚类算法得到混合数据聚类结果.但是，在实际应用中，面临的数据不仅是由数值型属性和分类属性共同描述的混合型数据，而且通常带有缺失值，是一种不完备混合数据.因此，如何针对不完备混合数据进行集成聚类就显得尤为必要.

为了解决这一问题，本文提出了一个基于缺失值填充的不完备混合数据的集成聚类算法.1)为了产生基聚类数据源的多样性，利用3种缺失值填充方法对缺失数据进行填充;2)分别针对每种填充方法得到的完备数据多次执行K原型(K-Prototypes)聚类算法[11]，从而形成一系列基聚类结果;3)构造一个相似度矩阵合并基聚类，进而通过集成技术得到最终的聚类结果.在UCI真实数据集上与传统聚类算法进行了实验比较分析，实验结果表明本文提出的算法是有效的.

1　相关工作

本节首先对本文中使用的缺失值填充方法及K-Prototypes聚类算法进行介绍.

1.1缺失值填充方法

针对缺失数据的处理问题，国内外学者提出了许多不同策略，其中填充法是一种最常用的技术[12].填充法利用数据集中的完备数据对每个缺失值进行估计，从而达到非完备数据完备化的目的.目前，研究者已经提出了多种填充方法，其中，平均值填充法及以K最近邻为基础的填充法由于简单有效得到了广泛的应用[13-16].下面分别对常用的3种缺失值填充方法进行介绍.

1) 平均值填充法

由于数值型属性和分类型属性的差异性，下面将分别对不同属性下缺失值的填充方法进行描述.如果缺失值对应的属性为分类型属性，根据统计学中众数(modes)的原理，用该属性下非缺失值样本中取值频数最多的值来对缺失值进行填充；如果缺失值对应的属性为数值型属性，则利用该属性下所有完备样本取值的平均值(means)来对缺失值进行填充.该方法利用现有完备数据的多数信息来推测缺失值，以最可能的取值来对缺失值进行填充，具有简单易实现的优点.但是，由于所有的填充值都集中于众数或均值，填充后的数据集在分布上容易形成尖峰，进而出现变量分布扭曲的问题，导致样本之间差异的弱化.

2)K最近邻填充法KNN

在K最近邻填充法中，一个样本的缺失值是通过找到与该样本最相似的K个完备样本，利用这K个完备样本的相关信息对缺失值进行填充.

(1)

样本x和y在分类型属性上的相异度DAc可表示为

(2)

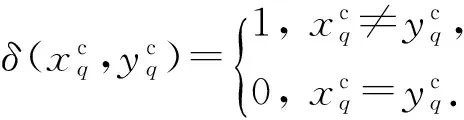
样本x和y的相异度计算如下：

(3)

其中，M(·)是一个函数，可以将样本x和y在数值型属性上的相异度DAr和分类型属性上的相异度DAc有效地结合起来以度量它们之间的相异性.

基于上述距离度量公式，K最近邻填充法主要流程描述如下：

算法1.K最近邻填充算法KNN.

Step1. 将数据集D划分为2个子集Dm和Dc，其中Dm表示由包括属性值缺失的样本组成的样本子集，Dc表示完备样本组成的样本子集.

Step2. 从集合Dm中提取出一个带有缺失值的样本xm.

Step2.1. 将带有缺失值的样本xm分成属性值完备和属性值缺失2部分.

Step2.2. 仅使用样本xm中属性值完备的部分来计算该样本和Dc集中所有样本的相异性.假设Dc集中的一个完备样本为xc，基于式(1)(2)，利用以下公式

D(xm,xc)=

(4)

来计算xm和xc的相异性.

Step2.3. 从完备样本集Dc中选择与带有缺失值的样本xm相异度最小的前K个完备样本组成集合DK.

Step2.4. 如果样本向量xm的缺失值对应的属性为分类型属性，用该属性下与xm相异度最小的K个样本DK中众数对缺失值进行填充；如果缺失值对应的属性为数值型属性，则取该属性下DK中K个样本的平均值来对缺失值进行填充.

Step3. 重复进行Step2，直至集合Dm中所有样本的缺失值都填充完毕.

作为一种填充方法，K最近邻填充法考虑了样本之间的相关性，填充结果较为准确，而且该方法具有简单易实现、计算高效的优点.然而，在属性值缺失较多的情况下，该方法的性能和准确性具有一定的缺陷.

3) 有序最近邻填充法SKNN

有序最近邻填充法SKNN是在KNN算法的基础上做了进一步的改进，算法主要流程如下：

算法2. 有序最近邻填充算法SKNN.

Step1. 将数据集D划分为2个子集Dm和Dc，其中，Dm表示由存在属性值缺失的样本组成的样本子集，Dc表示完备样本子集.

Step2. 将集合Dm中所有带有缺失值的样本按照缺失率(带有缺失值的属性个数占样本属性总数的比例)由低到高的顺序进行排序.

Step3. 从集合Dm中选择一个缺失率最低的样本，利用K最近邻法KNN从完备样本子集Dc中选出与该样本相异度最小的前K个完备样本对其缺失值进行填充.

Step4. 把填充后得到的完备样本加入完备数据子集Dc中.

Step5. 重复进行Step3～Step4，直至集合Dm中所有带有缺失值的样本填充完毕.

SKNN算法在填充过程中可以使用先前缺失数据填充得到的完备样本信息.与KNN填充算法相比，SKNN填充算法明显提高了对数据的利用率，在数据缺失率较大、完备数据样本相对匮乏的情况下，SKNN填充算法采取边填充边扩展完备数据样本的策略，充分地利用了缺失数据的信息，使得填充效果更加符合客观事实，填充效果更为合理.

1.2K-Prototypes算法介绍

文献[11]提出的K-Prototypes聚类算法是处理混合型数据最经济有效的一种算法.该算法在度量对象与类中心的相异性的过程中同时考虑了分类型属性和数值型属性部分的贡献.其中，对象与类中心在分类型属性下的相异性通过0-1简单匹配来度量，数值型属性下的相异性由欧氏距离表示.如果对象为分类型数据，则该算法将退化为K-Modes算法[11]；类似地，如果对象为数值型数据，则该算法退化为K-Means算法[17].因此，K-Prototypes算法实质上同时结合K-Modes算法和K-Means算法来解决现实世界中广泛存在的混合型数据的聚类问题.

假设在聚类过程中，由n个样本组成的混合型数据集合D={x1,x2,…,xn}在当前聚类中被划分为k个类Ck={C1,C2,…,Ck}，类原型为Zk={z1,z2,…,zk}，基于式(1)(2)，利用以下公式

(5)

来度量样本xi(1≤i≤n)和类原型zj(1≤j≤k)之间的相异性[18].

基于以上的相异性度量，K-Prototypes聚类算法描述如下：

算法3.K-Prototypes聚类算法.

Step1. 从数据集中随机选取k个不同的样本作为初始聚类中心.

Step2. 对数据集中的每个样本，根据式(5)计算其与每个类原型的相异性，将样本分配到与其最近的类原型所代表的类中.

Step3. 对于每个聚类结果，重新计算聚类原型.

Step4. 根据式(5)重新计算每个样本到新的类原型之间的相异性，根据最近邻原则重新分配样本.

Step5. 重复进行Step3～Step4，直到各个聚类中的样本不再发生变化为止.

2　不完备混合数据集成聚类算法

不完备混合数据的集成聚类算法主要分为4个阶段：第1阶段分别使用1.1节介绍的3种不同的缺失值填充方法对缺失值进行填充得到完备数据；第2阶段分别在填充后的完备数据集上基于随机产生初始类中心的方式多次进行K-Prototypes聚类算法，从而得到基聚类结果集Π(D)；第3阶段合并基聚类结果构造相似度矩阵SMn×n；第4阶段基于相似度矩阵运用层次聚类方法进行集成得到最终的聚类结果.本文算法的框架示意图如图1所示：

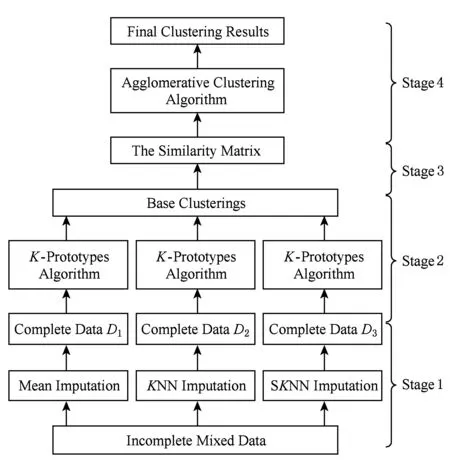
Fig. 1　The framework of the proposed algorithm.图1　本文算法框架

2.1生成基聚类

2.2获取集成关系

对于处理多个基聚类结果，现有的方法主要利用基聚类结果所提供的信息来得到数据集中样本之间的关联，构造一个相似度矩阵，然后基于此矩阵进行聚类集成，进而获得最终的聚类结果.

(6)

2) 根据所有基聚类产生的关系矩阵就可以得到样本之间的相似度矩阵SMn×n，其中样本xp和xq(1≤p,q≤n)之间的相似度表示为

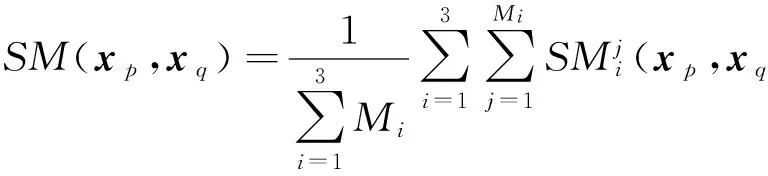
(7)

该矩阵的每个元素值由所有基聚类产生的关系矩阵对应元素的均值得到，反映了样本之间的相似度.传统的相似度度量方法往往完全依靠属性值来衡量样本之间的相似度，使得聚类结果不够准确，充分利用基聚类提供的信息来度量样本之间的相似性具有一定的有效性.

2.3确定最终聚类

在获取到集成关系的基础上，利用层次聚类算法来确定最终聚类.本文采用层次聚类算法自底向上的策略，首先将每个样本作为一个类，然后将2个相似度最大的类合并为一个类，重复循环此步骤，直到合并为k个类.

在层次聚类过程中假设有2个类C和C′，它们之间常用的3种相似性度量如下:

1) 单链(single link)方法.由2个类中相似度最大的2个样本决定.

(8)

2) 全链(complete link)方法.由2个类中相似度最小的2个样本决定.

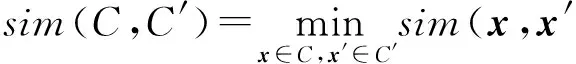
(9)

3) 组平均(average link)方法.由2个类中所有样本点相似度的平均值决定.

(10)

其中，样本之间的相似度sim(x,x′)为相似度矩阵SMn×n中的对应元素值.

2.4不完备混合数据的集成聚类算法

基于以上对不完备混合数据的集成聚类算法各个主要阶段的介绍，本文算法描述如下：

算法4. 不完备混合数据集成聚类算法.

输入：带有缺失值的数据集D、聚类个数k;

输出：最终聚类结果π*(D).

Step1. 对数据集D分别运用平均值填充法、KNN填充法、SKNN填充法填充得到完备数据集D1，D2，D3.

Step2. 对Di(1≤i≤3)分别执行Mi次K-Prototypes聚类算法，得到基聚类结果集Π(D).

Step3. 根据式(7)，计算样本与样本之间的相似度矩阵SMn×n.

Step4. 基于相似度矩阵SMn×n，分别根据式(8)(9)(10)运行层次聚类算法得到最终的聚类结果π*(D).

3　实验分析

3.1实验数据

为了验证本文提出算法的有效性，我们从UCI真实数据集中分别选取了数值型、分类型和混合型3种不同属性特征的不完备数据集进行了测试.数据集的信息描述如表1所示：

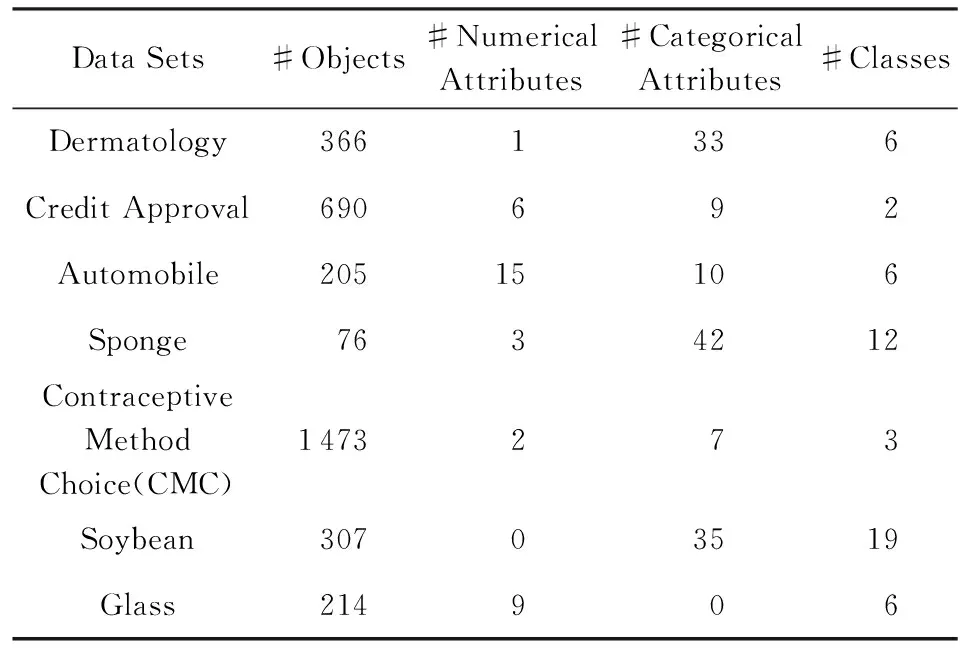
Table 1　The Summary of UCI Datasets

3.2聚类有效性度量指标

本文分别采用分类准确率(classification accuracy,CA)[19]、调整兰德系数(adjusted rand index,ARI)[19]，标准互信息(normalized mutual information,NMI)[4]三种评价指标对聚类结果进行评价.

(11)

其中,k为类个数，ai表示正确聚类为对应类别Ci的样本个数，n表示样本总数.

(12)

其中，

(13)

(14)

其中，nij表示聚类结果的第i个簇中包含原数据集类标签为j的样本总数，ni表示聚类结果的第i个簇的样本总数，nj表示原数据集类标签为j的样本总数，n表示样本总数；I和J分别表示聚类得到的簇个数和原数据集的类个数.

CA，ARI，NMI的值越大，表明聚类结果越好.

在下面的实验中，我们将本文提出的算法根据层次聚类过程中所选取的类间相似度度量方法分为single-link集成(SLCE)、complete-link集成(CLCE)、average-link集成(ALCE).将3种集成方法分别与用平均值填充、KNN填充、SKNN填充得到的完备数据进行单一的K-Prototypes聚类(分别简记为Mean_SK，KNN_SK，SKNN_SK)所得的聚类结果进行比较.

在实验过程中，针对表1所描述的CMC和Glass两个完备数据集，分别随机删除10%的属性值作为缺失数据.以下实验结果均为同一方法在相同的数据集上分别运行20次的CA，ARI，NMI的平均值和方差.其中本文提出的算法分别在每种填充方法得到的完备数据上进行50次K-Prototypes聚类算法来得到基聚类.

3.3实验结果分析

当KNN和SKNN填充法选取的最近邻个数K=5时，本文提出算法和其他聚类方法在不同评价指标下的实验结果的平均值及方差如表2～4所示：

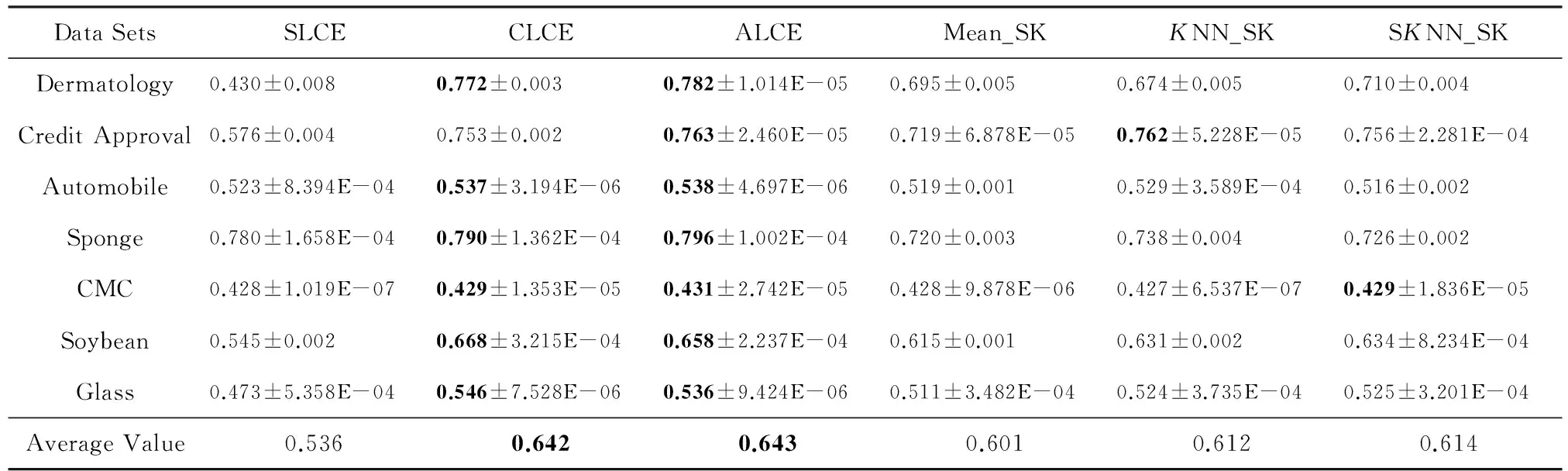
Table 2　Clustering Results of Different Algorithms with Respect to Mean±Var of CA

Table 3　Clustering Results of Different Algorithms with Respect to Mean±Var of ARI

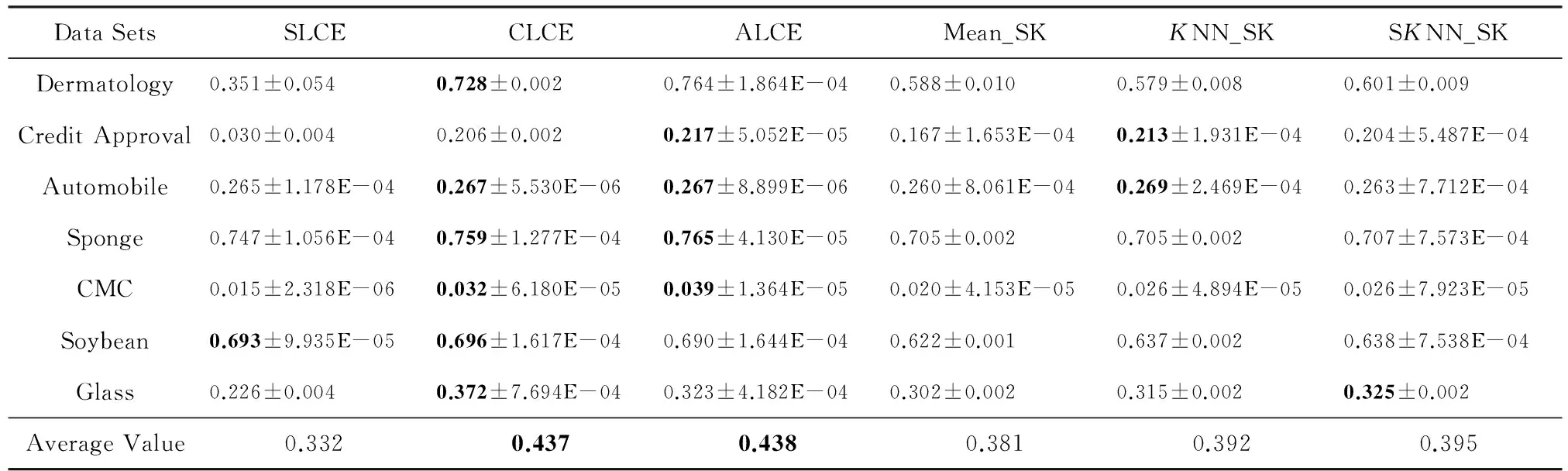
Table 4　Clustering Results of Different Algorithms with Respect to Mean±Var of NMI

Fig. 2　The performance of different algorithms with respect to different number of neighborhood on the Dermatology dataset.图2　数据集Dermatology上不同算法的聚类结果

其中，在每一数据集上不同方法的实验结果的最优值和次优值用粗体标识.通过表中数据分析可知，不论选取哪种指标作为评价标准，对于UCI中7个数据集，在多数情况下average-link集成和complete-link集成的聚类准确性优于其他算法，2种方法在所有数据集上的平均值都能达到最优值或次优值.average-link集成的性能比complete-link集成略好，这是因为complete-link集成确定类间距离时仅考虑有特点的数据，average-link集成考虑了类内数据的整体特点，因此在多数情况下，average-link集成得到的聚类准确性比较高，而complete-link集成表现出的性能次之.single-link集成确定类间距离时也只考虑了有特点的数据，而且没有考虑类内部的结构，所以表现出的聚类结果较差.此外，average-link集成在7个数据集上的方差都几乎为0，说明该方法具有较强的稳定性.

当KNN和SKNN填充法选取的最近邻个数K取不同值时，本文提出算法和其他聚类方法的实验结果如图2～8所示.由图2～8可知：

1) average-link集成和complete-link集成受到最近邻个数变化的影响较小，它们在多数情况下都能取到最优和次优的聚类结果.average-link集成在数据集Dermatology，Credit Approval，Sponge，CMC上的聚类准确度最高，在Automobile上的CA值和在Soybean上的ARI值也是较高的.complete-link集成在数据集Dermatology，Sponge，Soybean，Glass上表现出较高的性能，尤其在Glass上，complete-link集成的聚类性能明显优于average-link集成，这可能是由于Glass数据集的类结构比较紧凑，complete-link集成是取2个类中距离最远的2个样本点作为2个类的距离，这种集成方法就比较倾向于找到一些紧凑的类，所以该方法在这个数据集上的效果较优.

2) single-link集成除了在Sponge数据集上表现略好以外，在其他数据集上的聚类结果都不理想.这主要是由于single-link度量方法仅仅依靠距离最近的2个样本点来决定类间的差异性而没有考虑类内部的结构，因此聚类效果不佳.

3) Mean_SK，KNN_SK，SKNN_SK三种方法除了在Credit Approval数据集上表现较好外，在其他数据集上都明显不如average-link集成或complete-link集成.这是由于average-link集成和complete-link集成不仅对多次K-Prototypes聚类算法产生的多个基聚类进行集成，而且还将不同填充方法得到的完备数据集也作为产生基聚类的一种方法，这样就使得基聚类结果集更具有多样性，聚类结果的准确度也越高.

4) 随着最近邻个数K的变化，average-link集成和complete-link集成的实验结果是比较稳定的，它的性能对最近邻个数K的变化并不敏感，算法具有一定的鲁棒性.总之，average-link集成聚类方法在大多数数据集上都是较好的选择.

Fig. 3　The performance of different algorithms with respect to different number of neighborhood on the Credit Approval dataset.图3　数据集Credit Approval上不同算法的聚类结果

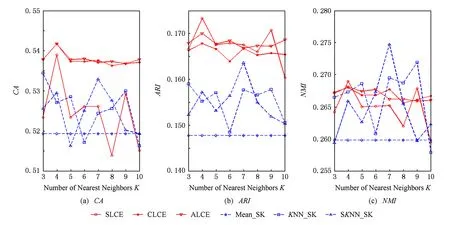
Fig. 4　The performance of different algorithms with respect to different number of neighborhood on the Automobile dataset.图4　数据集Automobile上不同算法的聚类结果

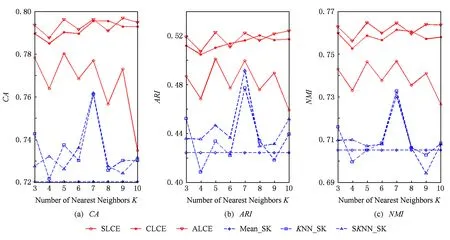
Fig. 5　The performance of different algorithms with respect to different number of neighborhood on the Sponge dataset.图5　数据集Sponge上不同算法的聚类结果

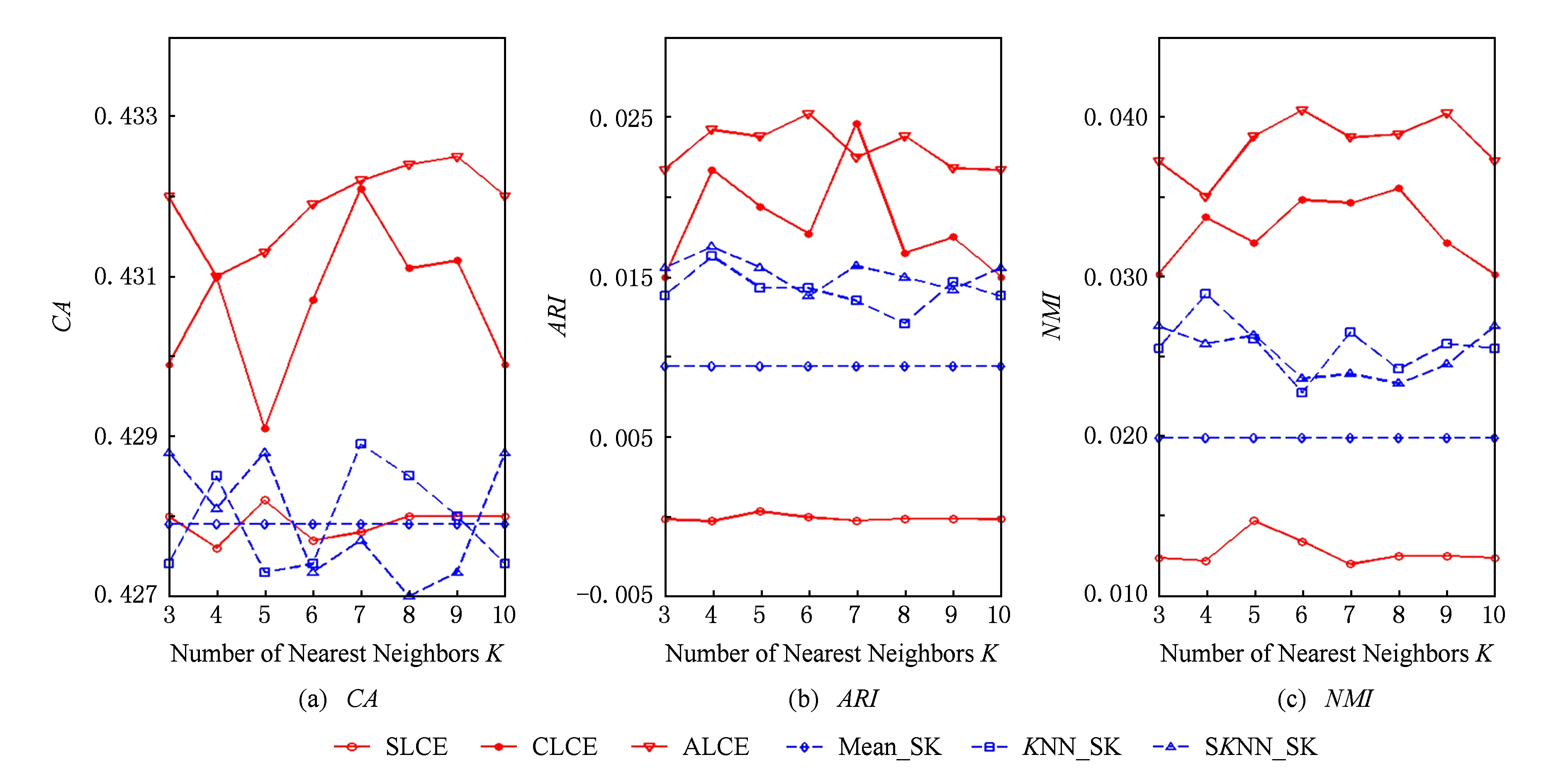
Fig. 6　The performance of different algorithms with respect to different number of neighborhood on the CMC dataset.图6　数据集CMC上不同算法的聚类结果

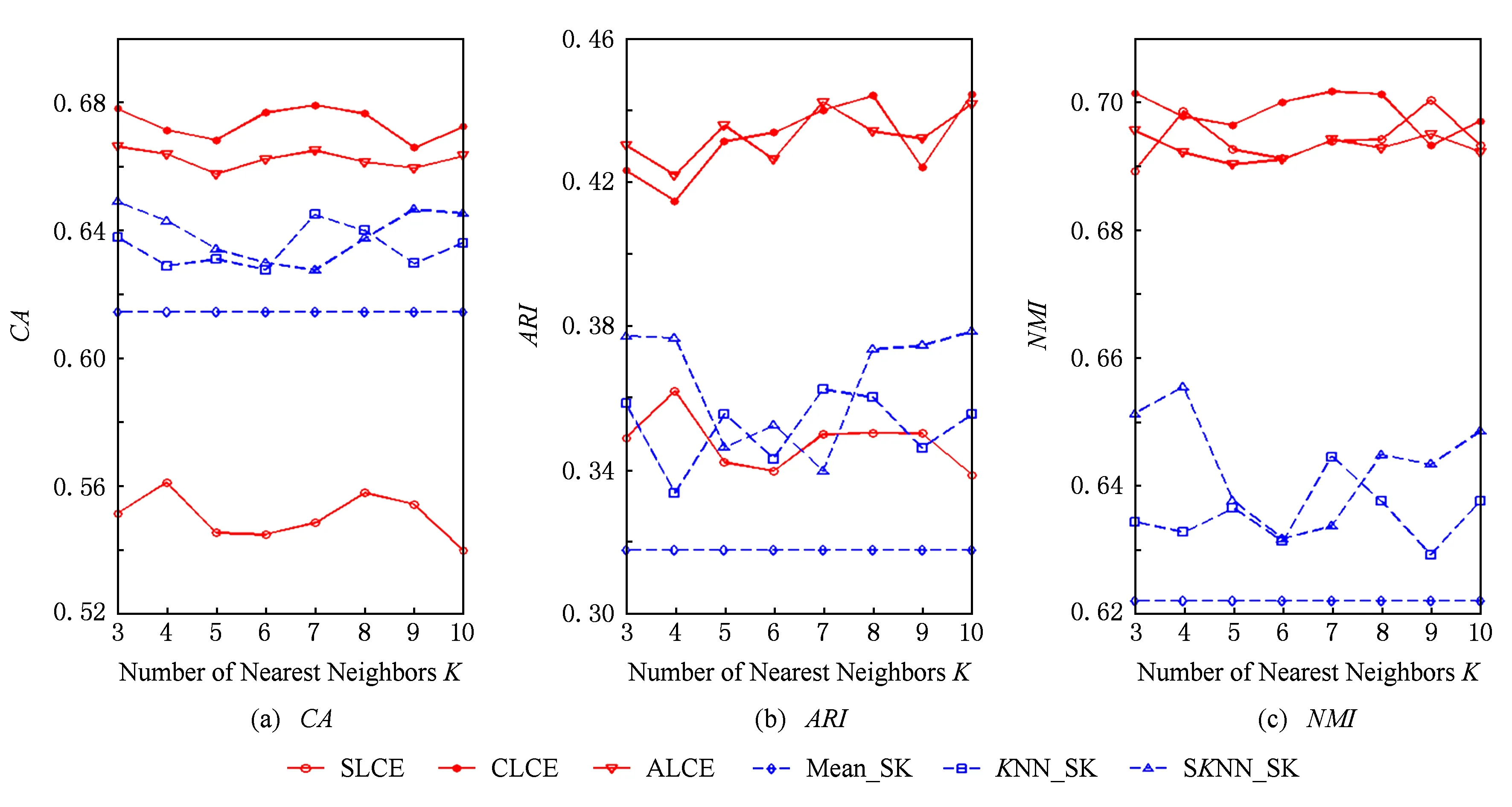
Fig. 7　The performance of different algorithms with respect to different number of neighborhood on the Soybean dataset.图7　数据集Soybean上不同算法的聚类结果

Fig. 8　The performance of different algorithms with respect to different number of neighborhood on the Glass dataset.图8　数据集Glass上不同算法的聚类结果

4　结　　论

本文针对不完备混合数据首先利用3种缺失值填充方法对缺失值进行填充得到完备数据集，有效地克服了单一填充方法带来的缺陷；其次在3种不同的完备数据集上基于随机产生初始类中心的方式多次执行K-Prototypes算法，从而形成一系列基聚类结果；最后构造一个相似度矩阵合并这些基聚类，进而利用层次聚类方法进行集成得到最终的聚类结果.在UCI真实数据集上进行了实验验证，与传统聚类算法相比，本文提出的算法可以获得较高的聚类质量.

然而，目前集成聚类算法面临着计算量大、时间复杂度较高的问题，在未来的工作中，我们将考虑如何提高算法的计算效率来解决大数据集成面临的挑战.

[1]Han Jiawei, Kamber M, Pei Jian. Data Mining: Concepts and Techniques [M]. 3rd ed. San Francisco, CA: Morgan Kaufmann, 2011[2]Sun Jigui, Liu Jie, Zhao Lianyu. Clustering algorithms research [J]. Journal of Software, 2008, 19(1): 48-61 (in Chinese)(孙吉贵, 刘杰, 赵连宇. 聚类算法研究 [J]. 软件学报, 2008, 19(1): 48-61)[3]Xu Rui, Wunsch D. Survey of clustering algorithm [J]. IEEE Trans on Neural Networks, 2005, 16(3): 645-678[4]Strehl A, Ghosh J. Cluster ensembles: A knowledge reuse framework for combining multiple partitions [J]. Journal of Machine Learning Research, 2002, 3: 583-617[5]Fred A L, Jain A K. Combining multiple clusterings using evidence accumulation [J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2005, 27(6): 835-850[6]Iam-On N, Boongoen T. Comparative study of matrix refinement approaches for ensemble clustering [J]. Machine Learning, 2015, 98(12): 269-300[7]Ghosh J, Acharya A. Cluster ensembles [J]. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2011, 1(4): 305-315[8]He Zengyou, Xu xiaofei, Deng Shengchun. Clustering mixed numeric and categorical data: A cluster ensemble approach[OL]. ArXiv cs0509011, 2005: 1-14 [2015-09-08]. http:arxiv.orgabscs0509011[9]Shaqsi J, Wang Wenjia. A clustering ensemble method for clustering mixed data[C]Proc of the Int Joint Conf on Neural Networks. Piscataway, NJ: IEEE, 2010: 1-8[10]Luo Huilan, Wei Hui. Clustering algorithm for mixed data based on clustering ensemble technique [J]. Computer Science, 2010, 37(11): 234-274 (in Chinese)(罗会兰, 危辉. 一种基于聚类集成技术的混合型数据聚类算法[J]. 计算机科学, 2010, 37(11): 234-274)[11]Huang Zhexue. Extensions to thek-means algorithm for clustering large data sets with categorical values [J]. Data Mining and Knowledge Discovery, 1998, 2(3): 283-304[12]Wu Sen, Feng Xiaodong, Shan Zhiguang. Missing data imputation approach based on incomplete data clustering[J]. Chinese Journal of Computers, 2012, 35(8): 1726-1738 (in Chinese)(武森, 冯小东, 单志广. 基于不完备数据聚类的缺失数据填补方法 [J]. 计算机学报, 2012, 35(8): 1726-1738)[13]Qiao Zhufeng, Tian Fengzhan, Huang Houkuan, et al. A comparison study of missing value datasets processing methods [J]. Journal of Computer Research and Development, 2006, 43(Suppl): 171-175 (in Chinese)(乔珠峰, 田凤占, 黄厚宽, 等. 缺失数据处理方法的比较研究 [J]. 计算机研究与发展, 2006, 43(增刊): 171-175)

[14]Silva L O, Zárate L E. A brief review of the main approaches for treatment of missing data [J]. Intelligent Data Analysis, 2014, 18(6): 1177-1198[15]Acock A C. Working with missing values [J]. Journal of Marriage and Family, 2005, 67(4): 1012-1028[16]Batista G E, Monard M C. An analysis of four missing data treatment methods for supervised learning [J]. Applied Artificial Intelligence, 2003, 17(5): 519-533[17]Macqueen J. Some methods for classification and analysis of multivariate observations [C]Proc of the 5th Berkeley Symp on Mathematical Statistics and Probability. Berkeley, CA: University of California Press, 1967: 281-297[18]Liang Jiye, Zhao Xingwang, Li Deyu, et al. Determining the number of clusters using information entropy for mixed data [J]. Pattern Recognition, 2012, 45(6): 2251-2265[19]Liang Jiye, Bai Liang, Dang Chuangyin, et al. Thek-means-type algorithms versus imbalanced data distributions [J]. IEEE Trans on Fuzzy Systems, 2012, 20(4): 728-745

Shi Qianyu, born in 1992. Master candidate. Student member of China Computer Federation. Her main research interests include data mining and machine learning (m15735170907@163.com).

Liang Jiye, born in 1962. Professor and PhD supervisor. Distinguished member of China Computer Federation. His main research interests include granular computing, data mining and machine learning (ljy@sxu.edu.cn).

Zhao Xingwang, born in 1984. PhD candidate. Member of China Computer Federation. His main research interests include data mining and machine learning (zhaoxw84@163.com).

A Clustering Ensemble Algorithm for Incomplete Mixed Data

Shi Qianyu, Liang Jiye, and Zhao Xingwang

(SchoolofComputerandInformationTechnology,ShanxiUniversity,Taiyuan030006)(KeyLaboratoryofComputationalIntelligenceandChineseInformationProcessing(ShanxiUniversity),MinistryofEducation,Taiyuan030006)

Cluster ensembles have recently emerged a powerful clustering analysis technology and caught high attention of researchers due to their good generalization ability. From the existing work, these techniques held great promise, most of which generate the final results for complete data sets with numerical attributes. However, real life data sets are usually incomplete mixed data described by numerical and categorical attributes at the same time. And these existing algorithms are not very effective for an incomplete mixed data set. To overcome this deficiency, this paper proposes a new clustering ensemble algorithm which can be used to ensemble final clustering results for mixed numerical and categorical incomplete data. Firstly, the algorithm conducts completion of incomplete mixed data using three different missing value filling methods. Then, a set of clustering solutions are produced by executingK-Prototypes clustering algorithm on three different kinds of complete data sets multiple times, respectively. Next, a similarity matrix is constructed by considering all the clustering solutions. After that, the final clustering result is obtained by hierarchical clustering algorithms based on the similarity matrix. The effectiveness of the proposed algorithm is empirically demonstrated over some UCI real data sets and three benchmark evaluation measures. The experimental results show that the proposed algorithm is able to generate higher clustering quality in comparison with several traditional clustering algorithms.

clustering ensemble; incomplete data; mixed data; missing value imputation;K-Prototypes clustering algorithm

2015-06-19；

2015-11-16

国家自然科学基金重点项目(61432011)；国家自然科学基金项目(61573229,61502289)；山西省科技基础条件平台建设项目(2012091002-0101)；山西省自然科学基金项目(201601D202039)；山西省研究生教育创新项目(2016SY002)

赵兴旺(zhaoxw84@163.com)

TP391

This work was supported by the Key Program of the National Natural Science Foundation of China(61432011), the National Natural Science Foundation of China(61573229, 61502289), the Construction Project of the Science and Technology Basic Condition Platform of Shanxi Province(2012091002-0101), the Natural Science Foundation of Shanxi Province of China (201601D202039), and the Graduate Education Innovation Project of Shanxi Province (2016SY002).