任务调度算法中新的自适应惯性权重计算方法

李学俊　徐　佳　朱二周　张以文

(安徽大学计算机科学与技术学院　合肥　230601)



任务调度算法中新的自适应惯性权重计算方法

李学俊徐佳朱二周张以文

(安徽大学计算机科学与技术学院合肥230601)

(xjli@ahu.edu.cn)

粒子群算法(particle swarm optimization, PSO)是解决云计算环境中工作流系统的任务调度优化问题的主流智能算法.然而基于传统自适应惯性权重的粒子群任务调度算法易陷入局部最优，导致调度方案的执行时间与费用较高.因此，通过改进单个粒子的成功值计算方法，提出了一种新的自适应惯性权重计算方法NAIWPSO(new adaptive inertia weight based particle swarm optimization).该方法通过比较每个粒子的适应度与全局最优值，可以更加精确描述粒子状态，进而提高了权重的自适应性.在新惯性权重基础上，提出了一种解决云工作流系统中任务调度优化问题的改进粒子群算法.新权重可以更准确的调整粒子速度，使算法更好地平衡粒子全局与局部搜索，避免陷入局部最优，获得执行费用更优的调度方案.实验表明，与5种已有惯性权重算法比较，新算法收敛稳定、适应度最低、执行费用平均减少18%.

云计算；工作流；任务调度；粒子群算法；惯性权重

工作流系统能够根据用户的需求管理与优化工作流的任务调度[1].云计算是一种高效、可伸缩、高可靠性的网络资源模型[2]，为用户快速分配与回收各种资源(包括网络、服务、存储、应用资源等)[3-4].随着云环境中科学计算、大规模电子商务等应用的发展，用户的服务质量(quality of service, QoS)要求不断提高，系统应用的运行费用急速上涨[5].因此，如何在满足QoS约束的前提下降低云环境中工作流运行费用是一个值得研究的问题[6].在文献[7]中，Yu等人提出了一种在网格计算环境中最小化任务执行费用的工作流调度算法.Wieczorek等人[8]使用HEFT任务调度算法较好地解决了网格计算环境中科学工作流调度问题.Xu等人[9]提出了一种在大量任务情况下的资源分配模型，有效降低了资源使用费用.云工作流管理系统可以根据用户的需求为每个任务分配合适的资源，有效降低云计算环境中工作流的运行费用[10-15].

目前云工作流管理系统中最常使用的任务调度算法为Eberhart和Shi[16]于1998年提出的粒子群算法(particle swarm optimization, PSO).该算法最初是受到鸟群、鱼群等群体动物的合作性行为启发，进而利用群体智能建立的一个随机优化启发式算法[17].PSO算法具有参数少、易实现、收敛速度快等特性，已被广泛地应用于各种优化领域.然而PSO算法没有有效地控制粒子的速度，因此无法很好地平衡粒子全局与局部搜索能力，具有局部收敛的缺陷，导致无法在有限的迭代次数中找到最优解.

为了解决局部收敛的缺陷，粒子群算法的速度更新公式增加了惯性权重这一参数，以增强平衡粒子全局与局部搜索的能力[16].目前，惯性权重大体上分为3类：常数或随机型惯性权重[16-18]、线性或指数变化惯性权重[19-21]、自适应性惯性权重[22].固定常数值惯性权重[16]实现简单，在算法执行过程中，惯性权重固定为一个常数，导致算法容易陷入局部最优.因此Eberhart和Shi[18]提出了随机惯性权重，以优化目标动态变化的问题.Shi和Eberhart[19-20]又提出线性减少惯性权重，以提高粒子群算法的求精能力，该算法如果在初期粒子搜索不到较好的位置点，易陷入局部最优.在线性减少惯性权重的基础上，Chatterjee和Siarry[21]提出了指数减少惯性权重，在一定程度上避免了算法陷入局部最优.然而，指数值的确定是一个难点，而且算法的计算量较大，不适合复杂优化问题求解.

综合上述非自适应惯性权重，Nickabadi等人[22]提出了基于自适应惯性权重(adaptive inertia weight, AIW)的粒子群算法(adaptive inertia weight based particle swarm optimization, AIWPSO).该算法可以在算法迭代过程中根据整个粒子群中粒子的位置状态信息对惯性权重进行动态地调整，提高PSO算法的寻优能力.然而，该参数中的成功值计算方法只考虑了单个粒子在不同迭代次数中位置的优劣，造成了自适应机制无法精确地调整惯性权重，导致PSO算法速度调节不够精确，易陷入局部最优.因此，本文通过改进传统权重中的成功值计算方法，提出了一种新的自适应惯性权重(new adaptive inertia weight, NAIW)；并将基于新自适应惯性权重的粒子群算法(new adaptive inertia weight based particle swarm optimization, NAIWPSO)运用到解决云工作流任务调度优化问题.实验结果表明，NAIWPSO任务调度算法在算法收敛速度、适应度和执行费用3方面均优于其余5种(固定、线性、指数、随机、传统自适应)惯性权重的粒子群算法.

1　自适应惯性权重

本节首先介绍了表示粒子位置状态优劣的适应度计算方法；然后分析了传统自适应惯性权重在成功值计算方面存在粒子位置状态表示不全面的不足；最后，提出了一种新的自适应惯性权重，改进了成功值计算公式.该权重可以更加精确地调整粒子速度，使算法更好地平衡粒子全局与局部搜索，达到避免算法局部收敛、搜索到最优值的目的.

1.1适应度

适应度是评价任务调度方案执行时间和费用的一项综合指标[2]，表示粒子群算法中粒子位置状态的优劣，如式(1)所示.适应度可以全面衡量该调度方案所需的时间与费用.适应度越高的调度方案，所需时间与费用的开销也就越大，粒子位置状态就越不好；相反，开销越小，粒子位置状态就越好.

(1)

适应度的计算分为3个部分：1)完工时间未超出截止期限时(f1=1，f2=0)的虚拟机运行费用；2)完工时间超出截止期限时(f1=0，f2=1)的虚拟机运行费用；3)各虚拟机的空闲时间wastetime之和.其中，makespanSk表示调度方案Sk中所有任务的最大完工时间；deadline表示整个工作流的截止期限，可以在deadlinemin～deadlinemax之间变化.deadlinemin与deadlinemax的计算方法如式(2)、式(3)：

deadlinemin=min{makespanSk}；

(2)

deadlinemax=max{makespanSk}.

(3)

在适应度计算式(1)中，costSk为某一调度方案Sk的费用值，其计算方法如式(4)所示：

(4)

1.2传统的自适应惯性权重

在文献[22]中，Nickabadi等人提出了一种自适应性惯性权重AIW，该权重首先计算单个粒子的成功值(如式(5)所示)，之后计算整个粒子群的成功率(如式(6)所示)，最后更新惯性权重(如式(7)所示).

(5)

(6)

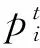
(7)

(8)

算法AIWPSO产生的调度方案执行时间和费用比普通PSO算法高.原因在于权重AIW中成功值计算公式S(i,t)只考虑了2种情况，即当前粒子的适应度优于上次，成功值则为1，反之则为0.由于该方法没有全面分析粒子的位置状态信息，即没有考虑全局最优位置，导致了成功率(式(6))以及惯性权重值(式(7))的计算不够准确.因此，该方法无法在每次迭代时精确地调整惯性权重值，造成算法在迭代过程中不能有效平衡粒子的全局与局部搜索，使算法易陷入局部最优，无法找到最优解.

1.3新的自适应惯性权重

针对传统惯性权重中单个粒子位置状态描述不全面的问题，本文在成功值计算方法中增加每个粒子的适应度与全局最优值比较，以更加精确地描述粒子所处的位置状态.权重NAIW中改进后的成功值如式(9)所示.在式(5)中每个粒子的当前适应度与上次迭代比较的基础上，式(9)中S(i,t)加入了全局最优值globalbestt.新的S(i,t)计算方法的取值扩充为3种情况：1，0.5，0.该方案基于对粒子位置状态更加细化的评价使得在粒子将要陷入局部最优解时，通过与全局最优适应度的比较来更加准确地得出S(i,t).精确的S(i,t)可以提高粒子群的成功率(式(6))的准确性和惯性权重(式(7))的自适应性.因此，算法可以更准确地调整粒子速度，以平衡粒子的全局与局部搜索能力，避免算法陷入局部最优.

(9)

算法NAIWPSO中的权重NAIW会随着粒子群的不同搜索状态而改变，可以动态改变粒子的速度.当粒子群的成功率PS(t)较大时，说明整个粒子群离最优值较远，此时需要粒子以较大的初速度进行全局搜索，通过式(7)和式(9)会提高速度更新式(8)中的w(t)的值，进而可以使粒子能够以较大的初速度接近最优值.当粒子群的成功率PS(t)较小时，说明整个粒子群已经接近最优值，通过式(7)和式(9)使w(t)值相应地减小，这样可以使粒子搜索时的速度下降，进而可以逐步精化最优解，保证了算法的精确度.综上，通过新的成功值计算公式，结合成功率与惯性权重更新公式，可以根据当前粒子群的位置状态不断改变粒子的速度，进而动态平衡算法的全局搜索与局部搜索能力.

2　基于新自适应惯性权重的粒子群任务调度算法

算法1. 基于新自适应惯性权重的粒子群任务调度算法.

输入：算法迭代次数Iteration、任务Tasks、虚拟机VMs、截止期限Deadline；

输出：最优调度方案Sbest.

① fori=1 tokdo

② 随机初始化任务调度方案Si及其搜索速度vi;

③ end for

④ fori=1 tokdo

⑤ 计算任务调度方案Si的适应度;

⑥ end for

⑦ 从k个任务调度方案中选出适应度最小的全局最优调度方案;

⑧ fori=1 toIterationdo

⑨ 根据搜索速度更新所有任务调度方案;

⑩ 为任务调度方案中的每一个任务重新分配虚拟机;

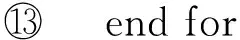
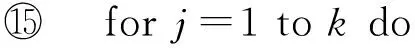
3　算法示例分析

首先给出了一个云工作流示例，然后比较分析传统自适应惯性权重的粒子群任务调度算法AIWPSO以及本文所提出的任务调度算法NAIWPSO，所生成调度方案的执行时间与费用.

工作流由若干个相互依赖的任务组成[1].工作流通常使用有向无环图(directed acyclic graph, DAG)来表示任务的执行先后顺序以及任务之间的相互依赖关系[2, 25].在DAG图中每一个节点都代表工作流中的1个任务，节点之间的连线代表任务之间的依赖关系.图1反映了1个工作流中5个任务的执行先后顺序：任务B和C必须在任务A执行完成后才能开始执行；而任务D必须在任务C执行完成后才能开始执行；当最后1个任务E执行完成后，代表该工作流全部完成.假定各任务在小型机上的执行时间是中型机的1.3倍，是大型机的1.6倍.同时，小型机、中型机和大型机的每单位时间价格(USD)分别为：0.12, 0.24, 0.48.图1中各任务在3种虚拟机上的执行时间如表1所示.下面将分别使用传统自适应惯性权重的粒子群任务调度算法AIWPSO以及本文所提出的任务调度算法NAIWPSO对图1表示的工作流进行任务调度.

Fig. 1　Example of workflow.图1　工作流示例

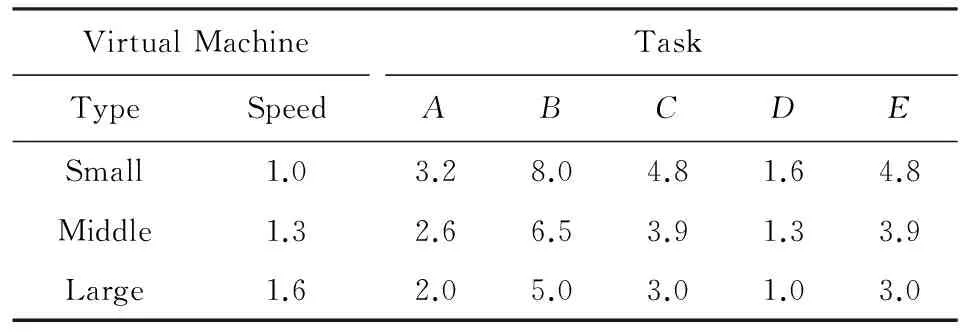
VirtualMachineTaskTypeSpeedABCDESmall1.03.28.04.81.64.8Middle1.32.66.53.91.33.9Large1.62.05.03.01.03.0

假设云环境中3台虚拟机(小型、中型、大型各1台)执行图1中的工作流.图2(a)为使用任务调度算法AIWPSO产生的调度方案，执行时间为16.7单位时间，费用为4.3USD;图2(b)展示了本文所使用的算法NAIWPSO所得到的调度方案，执行时间为14.6单位时间，费用为3.98USD.从图2可以看出，算法NAIWPSO所得到的调度方案相比算法AIWPSO，执行时间减少了2.1单位时间，费用减少了0.32USD.因此，新算法NAIWPSO相比AIWPSO能够有效降低云环境下任务调度的执行时间与费用.

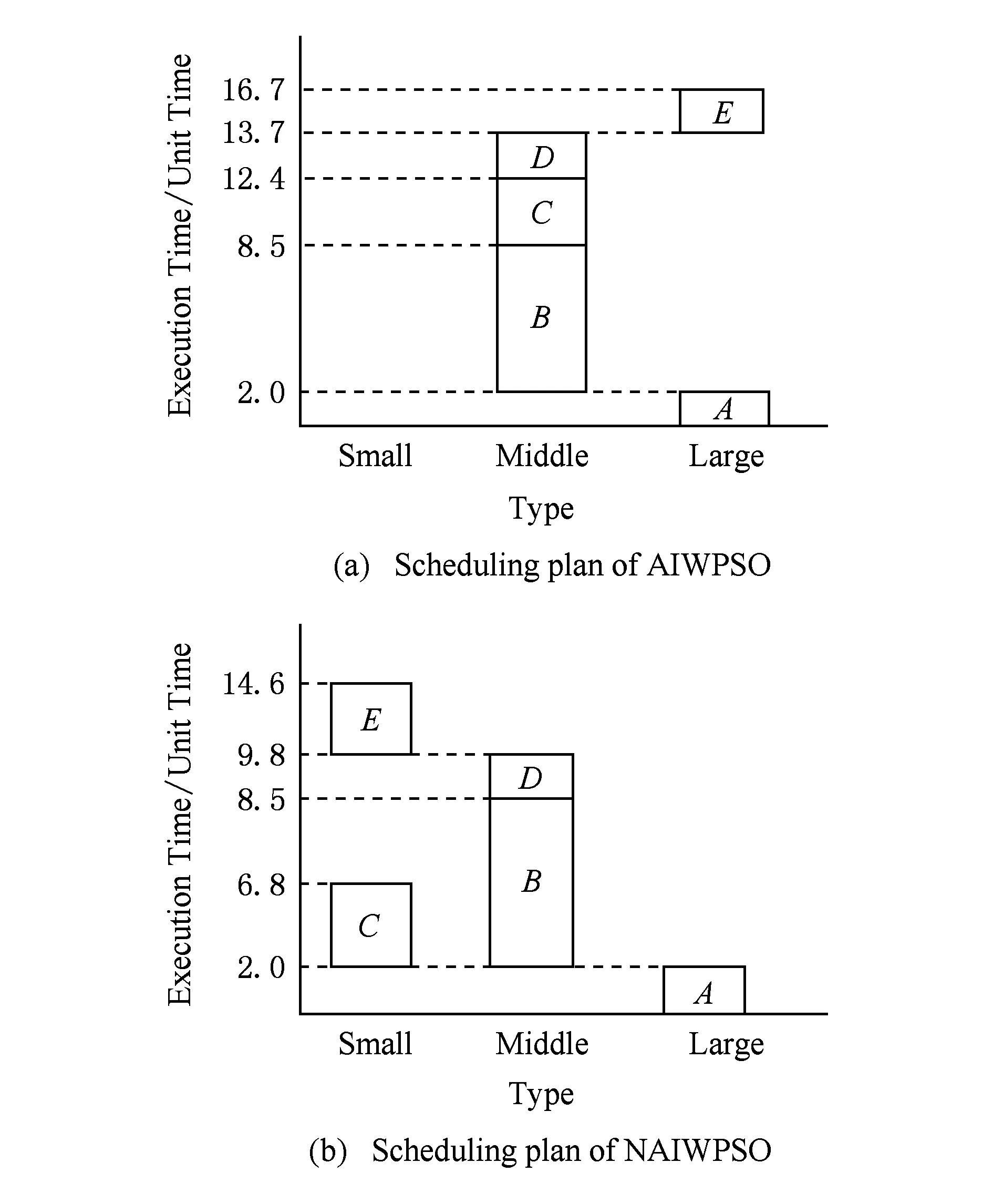
Fig. 2　Scheduling plan of two algorithms.图2　2个算法的调度方案

4　实验分析

本节首先详细给出了实验环境及算法参数设置；然后从算法收敛、适应度、执行费用3个方面将本文算法NAIWPSO与其他5种已有算法进行了对比分析；最后，为了对不同规模工作流的截止期限约束设置提供依据，给出了算法NAIWPSO生成调度方案的执行费用随截止期限的变化情况.

4.1实验环境与算法参数

本文实验采用Matlab 2010编写，运行在环境为Intel core i3 3.0 GHz CPU、2 GB内存的PC机上.为了评价和分析文中算法的性能，将常数值(constant)、指数减小(index-decreasing)、线性(linear decreasing)、 随机(random)、传统自适应(AIW)、新自适应(NAIW)这6种惯性权重应用到PSO任务调度算法中，对应的PSO算法分别表示为CPSO，IPSO，LPSO，RPSO，AIWPSO，NAIWPSO.实验所使用的亚马逊EC2(Amazon EC2①http:aws.amazon.comcnec2pricing)计价模型与虚拟机运行速度[2]如表2所示：

Table 2　Pricing Model of Amazon

实验对象工作流采用DAG图方式随机生成，每个工作流总任务数为50～300，单个任务的负载量是30～3 000范围内的随机值[26].PSO算法中粒子数量为30，虚拟机数量为4，学习因子c1与c2均为2[2]，惯性权重的最小值与最大值分别为0，1[22].各算法均取不同任务值情况下运行100次的平均值.

4.2实验结果与分析

本节从算法收敛、适应度、执行费用3个方面比较本文算法NAIWPSO 与其他5种算法.算法收敛表示算法找到最终解的速度，适应度是调度方案在时间、执行费用、虚拟机使用效率3个方面的综合评

价标准，执行费用为调度方案执行所需费用的虚拟机计算费用.

4.2.1算法收敛

6种算法生成调度方案的收敛情况表3所示.任务数为50和300时，生成调度方案适应度的6种算法收敛情况如图3～4所示.从表4可以看出，本文算法NAIWPSO在不同任务数情况下得出最优调度方案的迭代次数较为稳定，整体上优于传统的自适应算法AIWPSO.从图3和图4可以看出，算法NAIWPSO生成调度方案的适应度均优于其他5种算法，而且任务规模越大，优化效果越显著.

Table 3　Convergence for Six Algorithms in Different Tasks

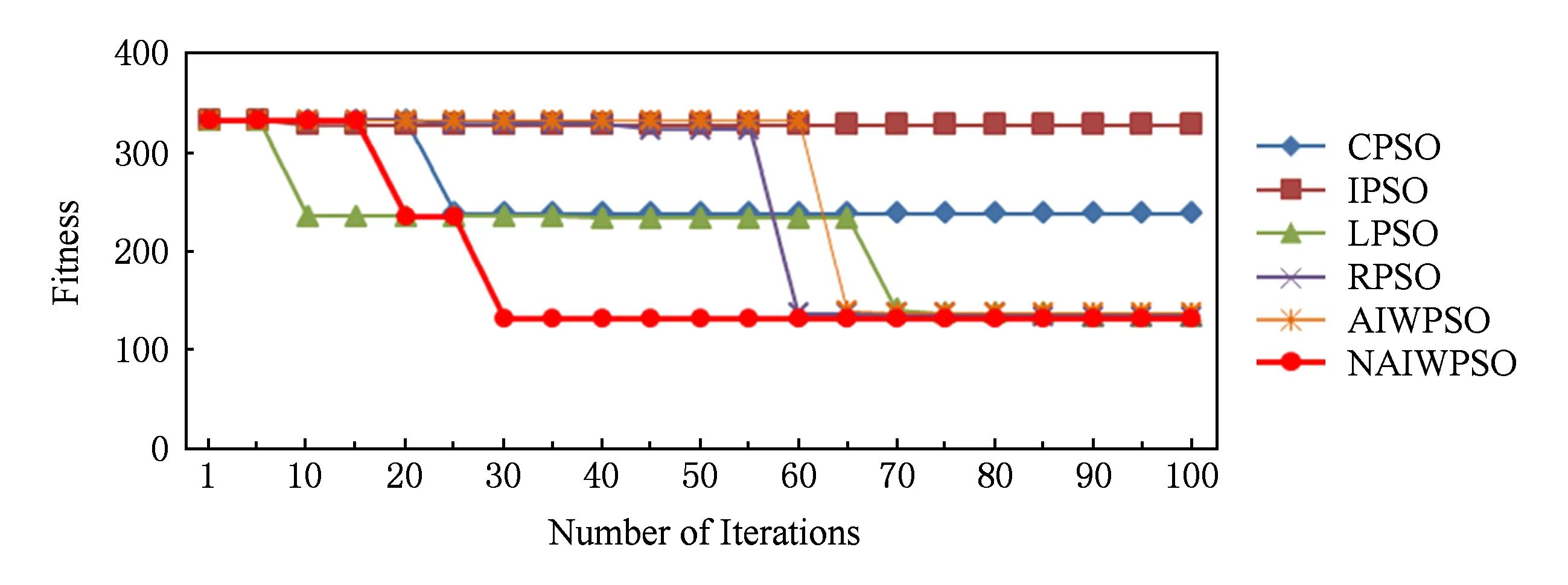
Fig. 3　Convergence of six algorithms for 50 tasks.图3　任务数为50时算法收敛情况

Fig. 4　Convergence of six algorithms for 300 tasks.图4　任务数为300时算法收敛情况

4.2.2适应度

在传统自适应惯性重的成功值计算方法的基础上,扩充了适应度优于上次且不优于全局最优值时取值0.5的情况，该值是根据经验设定的.为了说明取值的合理性，任务数取50～300，成功值取0.1～1.0，算法NAIWPSO的调度方案适应度变化如图5所示.本文算法NAIWPSO中成功值计算方法(式(9))第2种情况取值为0.5，与其他5种算法生成调度方案的适应度如图6所示.

从图5可以看出，对于不同任务规模的工作流，成功值取值为0.5时，算法NAIWPSO所得任务调度方案的适应度均最低.因此本文算法NAIWPSO中改进的成功值计算方法(式(9))第2种情况取值为0.5是合理的.图6中算法NAIWPSO生成调度方案的适应度均优于其他5种算法.任务数为50时，AIWPSO与NAIWPSO算法的适应度十分接近；但随着任务数量的增长，2种算法所得调度方案的适应度差距不断增大.因此，本文算法更适合于大规模任务调度优化.

4.2.3执行费用与截止期限

6种算法产生的调度方案的执行费用如图7所示.为了给不同任务数情况下截止期限的最大值和最小值确定提供依据，任务数为50～300时，通过式(2)、式(3)计算截止期限的最小值与最大值如表4所示，任务调度算法NAIWPSO的调度方案费用随截止期限的变化情况如图8所示.图7中，随着任务量在50～300范围内变化，本文算法NAIWPSO所生成的调度方案费用值均最低，并且NAIWPSO算法的调度方案费用值与其他5种算法的差值越来越大.这说明NAIWPSO算法更加适用于任务数较多的情况.这是因为在任务数较小的情况下，各算法均进行小范围的局部搜索，使得权重NAIW对粒子全局与局部搜索能力的平衡优势无法体现；然而随着问题规模的增大和任务数的增加，更能体现NAIW权重的自适应性，更好地平衡全局与局部搜索.

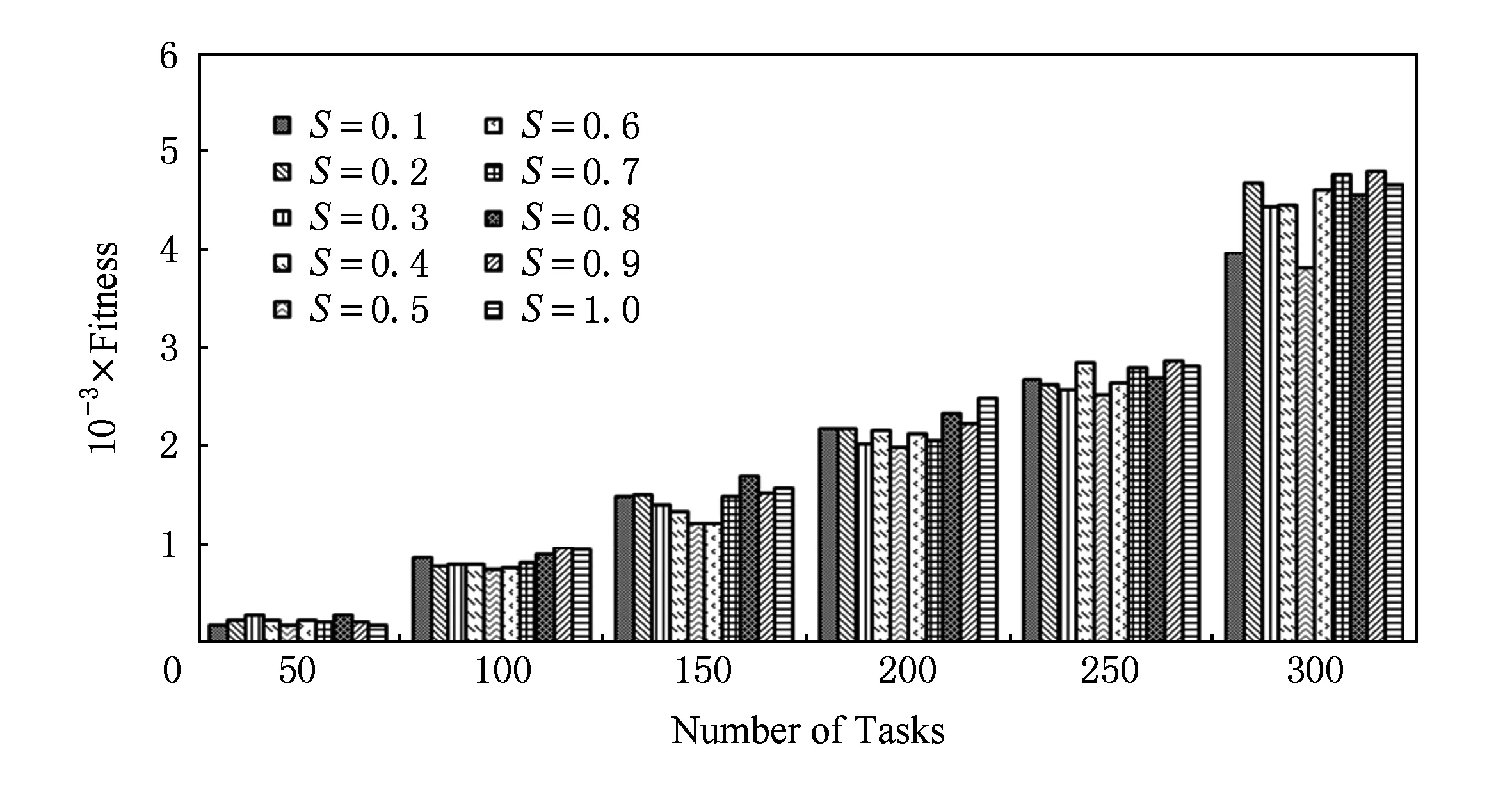
Fig. 5　Fitness of success value from 0.1 to 1.0.图5　不同成功值的适应度

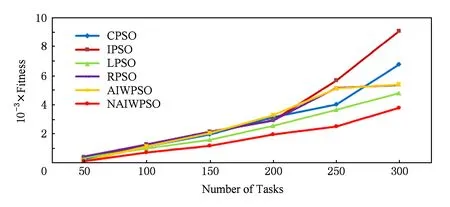
Fig. 6　Fitness of six algorithms.图6　6种算法的适应度

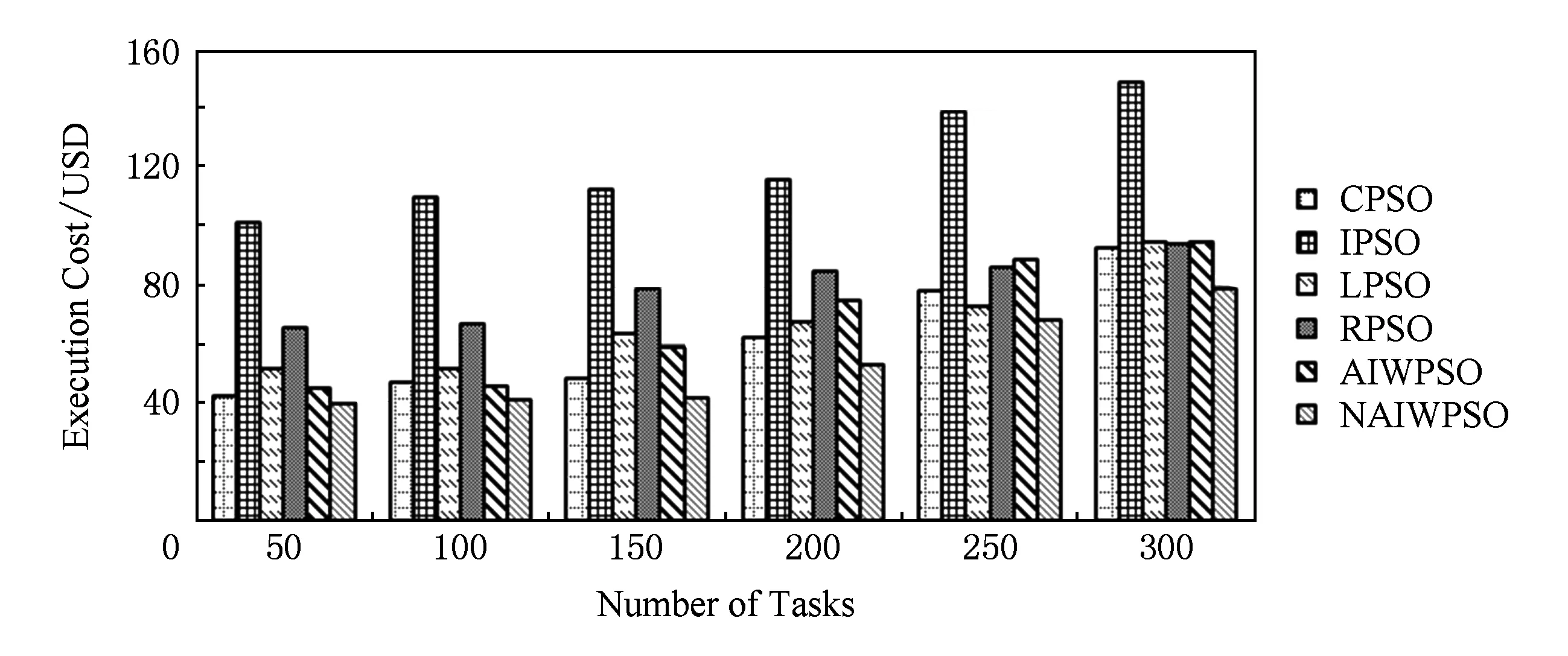
Fig. 7　Execution cost of six algorithms.图7　6种算法的执行费用

Table 4　The Minimum and Maximum Value of Deadline

Fig. 8　Execution cost with deadline constraint for different tasks.图8　不同任务规模中执行费用随截止期限的变化

从图8可以看出，当截止期限接近最小值时，算法可能没有合适的最优调度方案，这是因为当截止期限过小时，算法无法找到最优调度方案；当截止期限在最小与最大之间时，调度方案的费用值逐渐下降;当截止期限增长到一定范围时，调度方案费用值的执行费用都趋于稳定，这是由于在截止期限的值增长到某一时刻时所有任务都已被分配到费用最优的虚拟机上.本实验为云计算用户设置截止期限提供参考，例如任务数为300时，实验所得截止期限的最小值和最大值分别是31和45.

5　结束语

本文针对PSO算法中自适应惯性权重的成功值计算方法进行了改进，提出了新的自适应惯性权重，并设计了基于新惯性权重的任务调度算法NAIWPSO.新自适应惯性权重中的成功值计算方法比较了单粒子与全局最优粒子，可以更加精确地描述粒子所处的位置状态，从而提高权重的自适应性.因此，新自适应惯性权重可以更准确地调整粒子速度以平衡粒子的全局与局部搜索，使算法避免陷入局部最优，获得时间与费用更优的调度方案.实验结果表明，新的任务调度算法NAIWPSO算法收敛稳定、适应度和执行费用均优于其他5种算法.然而，本文DAG图表示的工作流模型中仅考虑了顺序、选择和循环3种任务关系，后续工作需要研究并发、互斥等不同任务关系对调度算法的影响.

[1]Dellman E, Gannon D, Shields M, et al. Workflows and e-science: An overview of workflow system features and capabilities[J]. Future Generation Computer Systems, 2008, 25(5): 528-540[2]Netjinda N, Sirinaovakul B, Achalakul T. Cost optimal scheduling in IaaS for dependent workload with particle swarm optimization[J]. The Journal of Supercomputing, 2014, 68(3): 1579-1603[3]Shi Xuelin, Xu Ke. Utility maximization model of virtual machine scheduling in cloud environment[J]. Chinese Journal of Computers, 2013, 36(2): 252-262 (in Chinese)(师雪霖, 徐恪. 云虚拟机资源分配的效用最大化模型[J]. 计算机学报, 2013, 36(2): 252-262)[4]Wang Peng, Huang Yan, Li Kun, et al. Load balancing degree first algorithm on phase space for cloud computing cluster[J]. Journal of Computer Research and Development, 2014, 51(5): 1095-1107(in Chinese)(王鹏, 黄焱, 李坤, 等. 云计算集群相空间负载均衡度优先调度算法研究[J]. 计算机研究与发展, 2014, 51(5): 1095-1107)[5]Wang Qiang, Li Xiongfei, Wang Jing. A data placement and task scheduling algorithm in cloud computing[J]. Journal of Computer Research and Development, 2014, 51(11): 2416-2426(in Chinese)(王强, 李雄飞, 王婧. 云计算中的数据放置与任务调度算法[J]. 计算机研究与发展, 2014, 51(11): 2416-2426)[6]Lee Y, Han H, Zomaya A, et al. Resource-efficient workflow scheduling in clouds[J]. Knowledge-Based Systems, 2015, 80(5): 153-162[7]Yu J, Buyya R, Tham C. Cost-based scheduling of scientific workflow applications on utility grids[C]Proc of the 1st IEEE Int Conf on e-Science and Grid Computing. Piscataway, NJ: IEEE, 2005: 1-8[8]Wieczorek M, Prodan R, Fahringer T. Scheduling of scientific workflows in the ASKALON grid environment[J]. ACM SIGMOD Record, 2005, 34(3): 56-62[9]Xu J, Liu C, Zhao X. Resource planning for massive number of process instances[C]Proc of the Move to Meaningful Internet Systems: OTM 2009. Berlin: Springer, 2009: 219-236[10]Wu Z, Liu X, Ni Z, et al. A market-oriented hierarchical scheduling strategy in cloud workflow systems[J]. The Journal of Supercomputing, 2013, 63(1): 256-293[11]Hoffa C, Mehta G, Freeman T, et al. On the use of cloud computing for scientific workflows[C]Proc of the 4th IEEE Int Conf on eScience. Piscataway, NJ: IEEE, 2008: 640-645[12]Sheng J, Wu W. Scheduling workflow in cloud computing based on hybrid particle swarm algorithm[J]. Telkomnika Indonesian Journal of Electrical Engineering, 2012, 10(7): 1560-1566[13]Pandey S, Wu L, Guru S, et al. A particle swarm optimization-based heuristic for scheduling workflow applications in cloud computing environments[C]Proc of the 24th IEEE Int Conf on Advanced Information Networking and Applications. Piscataway, NJ: IEEE, 2010: 400-407[14]Tao Q, Chang H, Yi Y, et al. QoS constrained grid workflow scheduling optimization based on a novel PSO algorithm[C]Proc of the 8th Int Conf on Grid and Cooperative Computing. Piscataway, NJ: IEEE, 2009: 153-159[15]Wu Z, Ni Z, Gu L, et al. A revised discrete particle swarm optimization for cloud workflow scheduling[C]Proc of 2010 Int Conf on Computational Intelligence and Security. Piscataway, NJ: IEEE, 2010: 184-188[16]Shi Y, Eberhart R. A modified particle swarm optimizer[C]Proc of 1998 IEEE Int Conf on Evolutionary Computation. Piscataway, NJ: IEEE, 1998: 760-766[17]Eberhart R, Shi Y. Particle swarm optimization: Developments, applications and resources[C]Proc of 2001 IEEE Int Conf on Evolutionary Computation. Piscataway, NJ: IEEE, 2001: 81-86[18]Eberhart R, Shi Y. Tracking and optimizing dynamic systems with particle swarms[C]Proc of 2001 Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2001: 94-100[19]Shi Y, Eberhart R. Empirical study of particle swarm optimization[C]Proc of 1999 Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 1999: 1945-1950[20]Eberhart R, Shi Y. Comparing inertia weights and constriction factors in particle swarm optimization[C]Proc of 2000 Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2000: 84-88[21]Chatterjee A, Siarry P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization[J]. Computers & Operations Research, 2006, 33(3): 859-871[22]Nickabadi A, Ebadzadeh M, Safabakhsh R. A novel particle swarm optimization algorithm with adaptive inertia weight[J]. Applied Soft Computing, 2011, 11(4): 3658-3670[23]Ho S, Lin H, Liauh W, et al. OPSO: Orthogonal particle swarm optimization and its application to task assignment problems[J]. IEEE Trans on Systems, Man and Cybernetics, Part A: Systems and Humans, 2008, 38(2): 288-298[24]Gong M, Wu Y, Cai Q, et al. Discrete particle swarm optimization for high-order graph matching[J]. Information Sciences, 2016, 328(1): 158-171[25]Rimal B, Jukan A, Katsaros D, et al. Architectural requirements for cloud computing systems: An enterprise cloud approach[J]. Journal of Grid Computing, 2011, 9(1): 3-26[26]Fard H, Prodan R, Fahringer T. A truthful dynamic workflow scheduling mechanism for commercial multicloud environments[J]. IEEE Trans on Parallel and Distributed Systems, 2013, 24(6): 1203-1212

Li Xuejun, born in 1976. PhD, associate professor. Member of China Computer Federation. His main research interests include workflow systems, cloud computing and intelligent software.

Xu Jia, born in 1992. Master candidate. His current research interests include intelligent algorithm and workflow systems (xujia_ahu@foxmail.com).

Zhu Erzhou, born in 1981. PhD, associate professor. His current research interests include program analysis, binary translation, compiling technology, virtualization and cloud computing.

Zhang Yiwen, born in 1976. PhD, associate professor. His current research interests include service computing, cloud computing and evolutionary algorithm.

A Novel Computation Method for Adaptive Inertia Weight of Task Scheduling Algorithm

Li Xuejun, Xu Jia, Zhu Erzhou, and Zhang Yiwen

(SchoolofComputerScienceandTechnology,AnhuiUniversity,Hefei230601)

Particle swarm optimization (PSO) is a primary intelligence algorithm to solve task scheduling problem for workflow systems in cloud computing. The inertia weight is one of the most important parameters to achieve a balance between the global and local search in PSO algorithm. However, traditional adaptive inertia weight-based PSO task scheduling algorithms usually get local optimal and cause longer execution time and higher cost for scheduling plan. The traditional adaptive inertia weight does not comprehensively represent the information of particle position, and then cannot make a suitable balance between global and local search. Hence, a novel computation method for adaptive inertia weight is proposed to improve the computation method of success value of each particle. This method shows the position state of each particle more accurately and then improves the adaptability of inertia weight by comparing the fitness of each particle with the global best particle. Then a new inertia weight-based PSO algorithm is presented to solve task scheduling problem for cloud workflow systems. The novel weight can adjust the particle velocity more correctly so that the algorithm avoids premature convergence by a proper balance between local and global search. Comparing our new adaptive inertia weight with other five traditional inertia weights (viz. constant, index decreasing, linear decreasing, random, and adaptive inertia weight), the results show that our new adaptive inertia weight-based scheduling algorithm can always achieve stable convergence speed, the optimal fitness and execution cost of the scheduling plan (i.e. roughly 18% reduction of execution cost).

cloud computing; workflow; task scheduling; particle swarm optimization (PSO); inertia weight

2015-12-22；

2016-04-19

国家自然科学基金项目(61300169)；安徽省教育厅自然科学研究重点项目(KJ2016A024)

TP391

This work was supported by the National Natural Science Foundation of China (61300169) and the Natural Science Foundation of Education Commission of Anhui Province (KJ2016A024).