随机傅里叶特征空间中高斯核支持向量机模型选择

冯　昌　　　廖士中

(天津大学计算机科学与技术学院　天津　300350)



随机傅里叶特征空间中高斯核支持向量机模型选择

冯昌廖士中

(天津大学计算机科学与技术学院天津300350)

(changfeng@tju.edu.cn)

模型选择是支持向量机(support vector machines, SVMs)学习的关键问题.标准支持向量机学习本质上是求解一个凸二次优化问题，求解的时间复杂度为数据规模的立方级，而经典的模型选择方法往往需要多次训练支持向量机，这种模型选择方法对于中等规模的支持向量机学习计算代价已较高，更难以扩展到大规模支持向量机学习.基于高斯核函数的随机傅里叶特征近似，提出一种新的、高效的核支持向量机模型选择方法.首先，利用随机傅里叶特征映射，将无限维隐式特征空间嵌入到一个相对低维的显式随机特征空间，并推导在2个不同的特征空间中分别训练支持向量机所得到的模型的误差上界；然后，以模型误差上界为理论保证，提出随机特征空间中核支持向量机的模型选择方法，应用随机特征空间中的线性支持向量机来逼近核支持向量机，计算模型选择准则的近似值，从而评价所对应的核支持向量机的相对优劣；最后，在标杆数据集上验证所提出方法的可行性和高效性.实验结果表明，所提出的模型选择方法与标准交叉验证方法的测试精度基本相当，但可显著地提高核支持向量机模型选择效率.

模型选择；支持向量机；随机傅里叶特征；高斯核；交叉验证

支持向量机(support vector machines, SVMs)是在统计学习理论基础上发展起来的一类重要的学习方法，是目前流行的数据挖掘方法之一[1-2].该方法在核诱导的特征空间中训练线性学习器，并应用泛化性理论来避免过拟合现象.

SVM的泛化性能主要依赖于核函数及模型参数的选择，不合适的选择将会导致过拟合(over-fitting)或欠拟合(under-fitting)，因此模型选择是SVM学习的重要问题.本文主要考虑高斯核SVM的模型选择问题，即核参数γ和特征空间中线性学习器正则化系数C的选择，其中(γ,C)合称为超参数[3].

已有的模型选择方法可概括为一个内外双层的优化框架[4]：内层在超参数固定的情况下在隐式特征空间中训练学习器，本质上是求解一个标准的凸二次优化问题；基于内层的学习结果，外层通过最小化泛化误差来调节超参数.k-折交叉验证(k-fold cross validation,k-CV)是泛化误差的有效估计[5]，被广泛应用在不同问题的学习过程中.对于参数空间中的每一组参数(γ,C)，k-CV需要训练学习器k次，因此计算代价较高.最小化泛化误差的理论上界是另外一类模型选择方法[6-7]，通常可以应用梯度下降算法实现.常见理论上界有半径间隔界(radius margin bound)[6]、span界[7]等.一般来说，在优化框架外层，基于理论上界的模型选择方法仅仅只需在梯度下降方向评估模型，不再需要搜索整个参数空间，从而提高模型选择效率，但是该类方法仍需多次训练SVM.

在核诱导的特征空间中训练线性学习器本质上是求解一个凸二次优化问题，求解时间复杂度为O(l3)，其中l为训练样本的个数.基于分解法实现的高效SVM求解器，最小序贯优化算法(sequential minimal optimization, SMO)，求解时间复杂度为O(l2)[8].若利用10折交叉验证模型选择，在10×10=100个(γ,C)参数组合上进行SVM学习，需要训练1 000个SVM；若应用理论上界方法进行模型选择，仍需要训练多个SVM.对于一般规模的数据，模型选择过程已十分耗时，更难扩展到大规模问题.

线性SVM研究引起了广泛关注.大量计算高效的线性SVM算法被提出，包括随机梯度下降算法[9]、割平面方法[10]、对偶坐标下降算法[11]等.利用具有线性时间复杂度的线性SVM算法，日常PC机就可以有效地处理大规模问题[12].但是对于非线性问题，线性SVM的预测准确率远不及核SVM.Rahimi和Recht[13]提出利用随机傅里叶特征近似高斯核函数，将核诱导的特征空间嵌入到一个显式的随机特征空间，从而可以应用高效的线性SVM一致逼近核SVM.该方法不但具有线性SVM的求解效率，而且能保持核SVM的预测精度.刘勇等人[14]基于高斯核的显式描述给出了另外一种显式特征映射方法,从而也能够应用线性算法求解非线性问题.该类方法将核SVM线性化，可很大程度地提升核SVM模型选择优化框架的内层效率.

对于模型选择而言，没有必要对每个模型都计算其精确结果，所需的仅是一个能够评估模型相对优劣且可快速计算的近似解.基于这一思想，核矩阵近似已经成功应用在支持向量机和最小二乘支持向量机的高效模型选择过程[15-17].本文基于高斯核函数的随机傅里叶特征近似，应用线性SVM近似核SVM，提出一种新的高斯核支持向量机模型选择方法.首先，证明随机特征空间中近似模型与其对应精确模型的误差上界.然后，在该误差上界的保证下，提出一种随机特征空间中核SVM模型选择的新方法.在模型选择优化框架内层，不再求解凸二次优化问题，而是将核诱导的特征空间嵌入到一个相对低维的显式随机特征空间，训练线性SVM，计算模型选择准则的近似值，评价对应核SVM的相对优劣.以k-折交叉验证模型选择实验为例，验证所提出的方法的有效性及高效性.实验结果表明，在模型选择标准数据集上，所提出的模型选择方法与标准交叉验证方法测试精度相当，但可显著地提高核SVM模型选择效率.

1　预备知识

首先简要回顾支持向量机，然后介绍高斯核函数的随机傅里叶特征近似.

1.1支持向量机

令S={(x1,y1),(x2,y2),…,(xl,yl)}∈(X ×Y)l表示样本集合，其中X为输入空间，Y为输出域.考虑二分类问题，即Y={-1,+1}，输入空间X ∈d.

软间隔SVM原优化问题描述如下：

(1)

其中，常量C>0，称为正则化参数.SVM的对偶问题为一个标准的凸二次优化问题：

(2)

(3)

通过上述优化过程可知，支持向量机的性能主要依赖于拉格朗日乘子、核函数、超参数的选择.然而，当核函数与超参数给定时，拉格朗日乘子可以通过优化过程求得.因此核函数与超参数的选择对SVM的性能起着决定性作用.不同的核函数表现能力不尽相同，其中高斯核是一种通用核，是使用最为广泛的支持向量机核函数，定义形式为

(4)

1.2随机傅里叶特征

定义1. 傅里叶变换与傅里叶逆变换.f(t)表示变量t的函数，如果f(t)满足Dirichlet条件：具有有限个间断点、有限个极值点，f(t)绝对可积，则

(5)

称为f(t)的傅里叶变换，且有

(6)

定理1. Bochner定理[19].连续函数f:d|→正定，当且仅当f为某一有限非负Borel测度μ的傅里叶变换，

(7)

只要核函数κ(·)选择合适，Bochner定理保证存在一个概率分布p(·)的傅里叶变换与κ(·)对应，即有如下推论.

推论1. 任一正定平移不变核k(x,y)=κ(x-y)均满足式(8):

(8)

其中，p(w)为w的概率密度函数.

对于高斯核函数，通过k(x,y)的傅里叶逆变换计算p(w),可得w～N (0,2γI)，其中I表示单位矩阵.易知

k(x,y)=Ew[e-iwT(x-y)]=Ew[cos(wT(x-y))]=

(9)

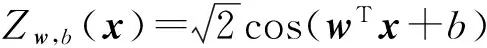
k(x,y)=E[〈Zw,b(x),Zw,b(y)〉],

(10)

则〈Zw,b(x),Zw,b(y)〉是高斯核函数的一个无偏估计.利用标准蒙特卡洛近似积分方法逼近高斯核，构造如下随机特征映射

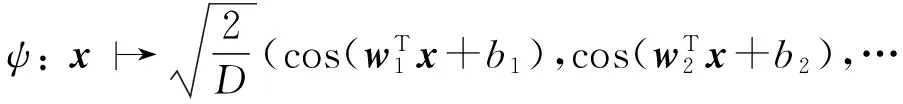
(11)

其中wi∈d是一个高斯随机向量，服从正态分布N (0,2γI);随机变量bi服从均匀分布U(-π,π)，i=1,2,…,D.同样有k(x,y)=E[〈ψ(x),ψ(y)〉].

2　随机特征空间中模型近似误差

算法1. 随机特征空间中线性SVM.

输出：随机特征空间中决策函数f.

① fori=1,2,…,Ddo

② 采样wi∈d：wi～N (0,2γI)；

③ 采样bi∈U [-π,π]；

④ endfor

⑤ for each (x,y)∈S do

⑥ 根据式(1)计算ψ(x)；

⑦ endfor

随机傅里叶特征方法通过近似高斯核函数，将原始数据映射到一个相对低维的有限维特征空间，并在新的特征空间中训练线性学习器，算法描述见算法1.本节将分析在随机特征空间中训练线性SVM得到模型与在原始数据空间上直接训练核SVM得到模型的误差上界.

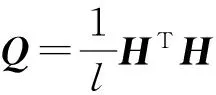
(12)

其中H=[ψ(x1)T,ψ(x2)T,…,ψ(xl)T].

命题1表明在Frobenius范数定义下，随机特征空间中潜在的近似核矩阵Q以O(1D)的收敛速度逼近K[20].

命题1. 对于任意δ∈(0,1)，下面的式(13)以1-δ的概率成立，

(13)

假设在训练数据S上利用核矩阵训练核SVM得到的假设记为f，在随机特征中训练线性SVM得到的假设记为f′，潜在的近似核矩阵为Q(注：训练线性SVM不需要计算核矩阵).对于任意x∈X，比较f(x)和f′(x)之间的差异.

命题2度量了SVM应用核矩阵得到的假设与应用近似核矩阵得到的假设之间的误差界[21].

命题2. 记h为利用核矩阵K∈l×l训练核支持向量机得到的假设，h′为利用近似核矩阵K′训练支持向量机得到的假设.进一步，对于所有x∈X，定义τ>0,使得k(x,x)≤τ及k′(x,x)≤τ.那么，对于所有x∈X如下不等式成立：

|h′(x)-h(x)|≤

(14)

其中C0为某一常量.

定理2. 模型近似误差界.对于任意δ∈(0,1)，所有x∈X，下列不等式以1-δ概率成立，

|f′(x)-f(x)|≤

(15)

证毕.

定理2给出了分别训练基于随机特征的线性SVM及对应高斯核SVM得到决策函数之间的误差上界.随着随机特征空间维度D的增加，该误差界将变得更小.该定理保证了,在随机特征空间中训练线性SVM得到的近似模型能够被用来评价在核诱导的特征空间中对应精确模型的相对优劣.

3　高斯核SVM模型选择

模型选择优化框架外层通过使得泛化误差最小化搜索参数空间，内层则训练多个核SVM.本节通过应用随机特征方法提升模型选择优化框架内层效率，即在优化框架内层利用基于随机特征的线性SVM近似核SVM.

对于模型选择而言，选择准则没有必要是泛化误差的无偏估计，近似准则值只要能够区分不同模型的相对优劣选择出最优的模型即可.由定理2可知，在随机特征空间中利用基于随机特征的线性SVM近似核SVM，得到的近似模型相对于精确模型有界.因此，能够利用此近似方法计算模型选择准则的近似值，从而高效地评价原核诱导的特征空间中对应模型的相对优劣.具体描述见算法2.

算法2. 基于随机傅里叶特征的近似模型选择算法AMS-RFF.

输出：(γ,C)opt.

① 初始化：(γ,C)=(γ0,C0);

② repeat

③ 利用算法1在训练集S上训练学习器，得到线性决策函数f；

④ 利用f计算模型选择准则T的值；

⑤ 若T的值减小则更新(γ,C)opt；

⑥ 在P中更新(γ,C);

⑦ until 准则T的值最小化；

⑧ 输出(γ,C)opt.

记l为训练样本规模，d为训练样本维度，D为随机傅里叶特征空间维度.训练高斯核SVM应用高效的SMO算法实现[8,22]，其计算时间复杂度为O(l2).线性支持向量机求解的时间复杂度为O(lD)[12].随机傅里叶特征映射的时间复杂度为O(lDd).

对于半径间隔界和Span界方法，需要在模型选择内层的每一次迭代完整地求解核SVM.记S为模型选择需要迭代的次数.标准核SVM模型选择时间复杂度为O(Sl2)，而算法2的时间复杂度为O(SdlD).

对于k-折交叉验证方法，记Sγ,SC分别表示参数γ,C格搜索的长度.标准核SVM模型选择时间复杂度为O(kSγSCl2).算法1中，随机特征映射时间复杂度为O(SγldD)，训练线性SVM的时间复杂度为O(kSγSClD)，因此算法2总的时间复杂度为O((d+kSC)SγlD).

4　实验结果与分析

交叉验证是一种广泛应用且有效的模型选择方法.以k-折交叉验证(k=5,10)为例，验证提出算法AMS-RFF的可行性及计算效率.实验中数据集为标准模型选择数据集[23]，如表1所示：

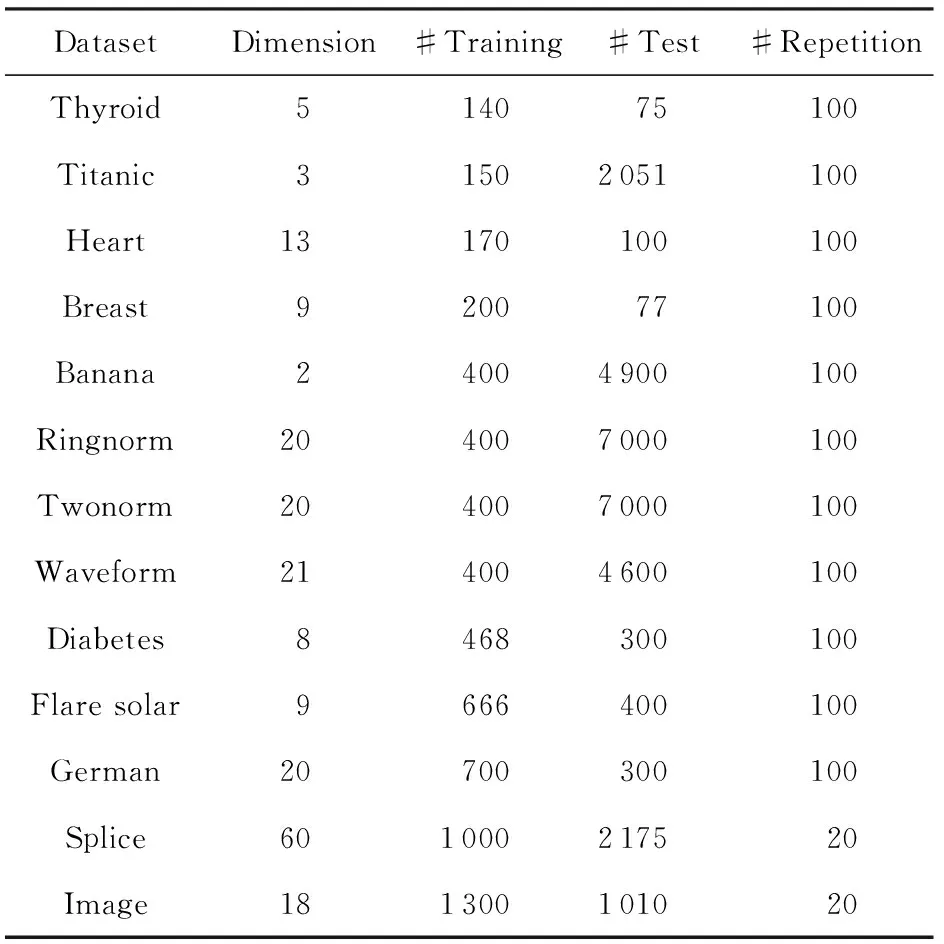
Table 1　Specification of Benchmark Datasets

为了消除数据划分带来的影响，每一个数据集根据训练集与测试集大小随机划分100次(对于Image和Splice各进行20次)，得到100组训练集和测试集.实验中，首先在训练集上进行模型选择得到最优参数组合，然后利用最优参数组合训练核SVM，最后在测试集上评价最优参数下的核SVM模型.应用统计分析方法评价模型选择算法.

使用LIBSVM[22]作为高斯核SVM的SMO算法实现，使用LIBLINEAR[12]训练线性SVM.实验环境为Core i5个人PC机，主频3.2 GHz，内存4 GB，算法实现采用C++语言.

核SVMk-折交叉验证模型选择过程记为k-CV，与之对应，在模型选择优化框架内层训练基于随机特征的线性SVM，进行k-折交叉验证过程记为Approximatek-CV(简写为Ak-CV),其中k=5,10.交叉验证在13×11大小的格搜索空间上进行，γ∈{2-15,2-13,…,29}，C∈{2-5,2-3,…,215}.算法1中随机特征空间维度统一设置为D=30.

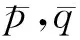
再看模型选择效率，对于所有13个数据集，仅仅在3个数据集上Ak-CV (k=5,10)没有带来效率上的提升，这3个数据集(Thyroid,Titanic,Heart)的数据量均小于200.对于数据规模较大的数据集，Ak-CV能带来效率上10倍甚至20倍的提升.随着数据量的增加，效率提升更加明显.这是因为所提出的方法与标准交叉验证方法在小规模数据上效率差异不大，随着数据规模的增加，所提出的方法效率提高越明显.

在数据集Splice和Image上进行另外一组实验，验证标准5-折交叉验证(5-CV)与所提出的方法(A5-CV)性能随着训练样本规模的变化情况，实验结果如图1和图2所示.随着训练样本规模的变化，2种模型选择方法选择的模型测试准确率相差不大(如图1所示).在模型选择的效率上，A5-CV的时间几乎与训练样本规模呈线性关系，而5-CV的时间与样本规模呈平方关系，这正好与第3节模型选择时间复杂度分析结果一致.因而，所提出的方法更加适用于大规模核方法模型选择问题.

Table 2　Comparison of Computation Time and Test Accuracy (Acc) of Model Selection among k-CV and Approximate

Fig. 1　The test accuracy varies with respect to the number of training samples.图1　测试准确率随着训练样本数的变化情况

Fig. 2　The time of model selection varies with respect to the number of training samples.图2　模型选择时间随着训练样本数的变化情况

5　结束语

核SVM优化问题求解的复杂度为O(l3)，基于分解策略的高效SMO算法求解的复杂度为O(l2)，其中l为训练样本的个数.模型选择过程往往需要多次训练核SVM，并且精确评估每一个模型，计算代价过高.针对这一问题，提出基于随机傅里叶特征的高斯核模型选择方法.通过随机傅里叶特征映射将数据映射到显式的随机特征空间，训练具有O(l)复杂度的线性SVM，进而可高效计算模型选择准则的近似值，大幅度提升模型选择效率.推导了随机特征空间中模型与对应核诱导的特征空间中模型的误差上界，从理论上保证了可利用随机特征方法评价原特征空间中模型的相对优劣.所提出的方法适用于大规模核SVM的模型选择.

进一步工作考虑随机特征空间维度D的选择问题.

[1]Vapnik V N. Statistical Learning Theory[M]. New York: John Wiley & Sons, 1998[2]Schölkopf B, Smola A J. Learning with Kernels: Support Vector Machines, Regularization, Optimization,and Beyond[M]. Cambridge, MA: MIT Press, 2002[3]Chapelle O, Vapnik V. Model selection for support vector machines[C]Advances in Neural Information Processing Systems 12. Cambridge, MA: MIT Press, 2000: 230-236[4]Guyon I, Saffari A, Dror G, et al. Model selection: Beyond the Bayesianfrequentist divide[J]. Journal of Machine Learning Research, 2010, 11: 61-87[5]Duan K, Keerthi S S, Poo A N. Evaluation of simple performance measures for tuning SVM hyperparameters[J]. Neurocomputing, 2003, 51: 41-59[6]Chapelle O, Vapnik V N, Bousquet O, et al. Choosing multiple parameters for support vector machines[J]. Machine Learning, 2002, 46(123): 131-159[7]Vapnik V N, Chapelle O. Bounds on error expectation for support vector machines[J]. Neural Computation, 2000, 12(9): 2013-2036[8]Platt J C. Fast Training of support vector machines using sequential minimal optimization[C]Advances in Kernel Methods: Support Vector Learning. Cambridge, MA: MIT Press, 1999: 185-208[9]Zhang T. Solving large scale linear prediction problems using stochastic gradient descent algorithms[C]Proc of the 21st Int Conf on Machine Learning. New York: ACM, 2004: 919-926[10]Joachims T. Training linear SVMs in linear time[C]Proc of the 12th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2006: 217-226[11]Hsieh C J, Chang K W, Lin C J, et al. A dual coordinate descent method for large-scale linear SVM[C]Proc of the 25th Int Conf on Machine Learning. New York: ACM, 2008: 408-415[12]Fan R E, Chang K W, Hsieh C J, et al. LIBLINEAR: A library for large linear classification[J]. Journal of Machine Learning Research, 2008, 9: 1871-1874[13]Rahimi A, Recht B. Random features for large-scale kernel machines[C]Advances in Neural Information Processing Systems 20. Cambridge, MA: MIT Press, 2007: 1177-1184[14]Liu Yong, Jiang Shali, Liao Shizhong. Approximate Gaussian kernel for large-scale SVM[J]. Journal of Computer Research and Development, 2014, 51(10): 2171-2177 (in Chinese)(刘勇, 江沙里, 廖士中. 基于近似高斯核显式描述的大规模SVM求解[J]. 计算机研究与发展, 2014, 51(10): 2171-2177)[15]Ding L, Liao S. Approximate model selection for large scale LSSVM[C]Proc of the 3rd Asian Conf on Machine Learning. Brookline, MA: Microtome Publishing, 2011: 165-180[16]Ding L, Liao S. Nyström approximate model selection for LSSVM[C]Proc of the 16th Pacific Asia Conf on Knowledge Discovery and Data Mining. Berlin: Springer, 2012: 282-293[17]Ding Lizhong, Liao Shizhong. Approximate model selection on regularization path for support vector machines[J]. Journal of Computer Research and Development, 2012, 49(6): 1248-1255 (in Chinese)(丁立中, 廖士中. 基于正则化路径的支持向量机近似模型选择[J]. 计算机研究与发展, 2012, 49(6): 1248-1255)[18]Kimeldorf G S, Wahba G. A correspondence between Bayesian estimation on stochastic processes and smoothing by splines[J]. The Annals of Mathematical Statistics, 1970, 41(2): 495-502[19]Rudin W. Fourier Analysis on Groups[M]. New York: John Wiley & Sons, 1962[20]Chitta R, Jin R, Jain A K. Efficient kernel clustering using random Fourier features[C]Proc of the 12th IEEE Int Conf on Data Mining. Piscataway, NJ: IEEE, 2012: 161-170[21]Cortes C, Mohri M, Talwalkar A. On the impact of kernel approximation on learning accuracy[C]Proc of the 13th Int Conf on Artificial Intelligence and Statistics. Brookline, MA: Microtome Publishing, 2010: 113-120[22]Chang C C, Lin C J. LIBSVM: A library for support vector machines[J]. ACM Trans on Intelligent Systems and Technology, 2011, 2: 27:1-27:27[23]Ratsch G, Onoda T, Müller K R. Soft margins for AdaBoost[J]. Machine Learning, 2001, 42(3): 287-320[24]Cawley G C, Talbot N L. Preventing over-fitting during model selection via Bayesian regularisation of the hyper-parameters[J]. Journal of Machine Learning Research, 2007, 8: 841-861[25]Demšar J. Statistical comparisons of classifiers over multiple data sets[J]. Journal of Machine Learning Research, 2006, 7: 1-30

Feng Chang, born in 1989, PhD candidate. Student member of China Computer Federation. His main research interests include kernel methods, model selection and randomized computation.

Liao Shizhong, born in 1964. PhD, professor, and PhD supervisor. Member of China Computer Federation. His main research interests include artificial intelligent and theoretical computer science.

Model Selection for Gaussian Kernel Support Vector Machines in Random Fourier Feature Space

Feng Chang and Liao Shizhong

(SchoolofComputerScienceandTechnology,TianjinUniversity,Tianjin300350)

Model selection is very critical to support vector machines (SVMs). Standard SVMs typically suffer from cubic time complexity in data size since they solve the convex quadratic programming problems. However, it usually needs to train hundredsthousands of SVMs for model selection, which is prohibitively time-consuming for medium-scale datasets and very difficult to scale up to large-scale problems. In this paper, by using random Fourier features to approximate Gaussian kernel, a novel and efficient approach to model selection of kernel SVMs is proposed. Firstly, the random Fourier feature mapping is used to embed the infinite-dimensional implicit feature space into an explicit random feature space. An error bound between the accurate model obtained by training kernel SVM and the approximate one returned by the linear SVM in the random feature space is derived. Then, in the random feature space, a model selection approach to kernel SVM is presented. Under the guarantee of the model error upper bound, by applying the linear SVMs in the random feature space to approximate the corresponding kernel SVMs, the approximate model selection criterion can be efficiently calculated and used to assess the relative goodness of the corresponding kernel SVMs. Finally, comparison experiments on benchmark datasets for cross validation model selection show the proposed approach can significantly improve the efficiency of model selection for kernel SVMs while guaranteeing test accuracy.

model selection; support vector machines (SVMs); random Fourier features; Gaussian kernel; cross validation

2015-06-12；

2015-10-30

国家自然科学基金项目(61170019)

廖士中(szliao@tju.edu.cn)

TP181; TP301

This work was supported by the National Natural Science Foundation of China (61170019).