代价敏感大间隔分布学习机

周宇航　　　周志华

(计算机软件新技术国家重点实验室(南京大学)　南京　210023)



代价敏感大间隔分布学习机

周宇航周志华

(计算机软件新技术国家重点实验室(南京大学)南京210023)

(软件新技术与产业化协同创新中心(南京大学)南京210023) (zhouyh@lamda.nju.edu.cn)

在现实生活中的很多应用里，对不同类别的样本错误地分类往往会造成不同程度的损失，这些损失可以用非均衡代价来刻画.代价敏感学习的目标就是最小化总体代价.提出了一种新的代价敏感分类方法——代价敏感大间隔分布学习机(cost-sensitive large margin distribution machine, CS-LDM).与传统的大间隔学习方法试图最大化“最小间隔”不同，CS-LDM在最小化总体代价的同时致力于对“间隔分布”进行优化，并通过对偶坐标下降方法优化目标函数，以有效地进行代价敏感学习.实验结果表明，CS-LDM的性能显著优于代价敏感支持向量机CS-SVM，平均总体代价下降了24%.

代价敏感学习；间隔分布；支持向量机；表示定理；对偶坐标下降法

在现实生活的很多应用中，对不同类别的样本错误地分类往往会造成不同程度的损失，这些损失可以用非均衡代价来刻画.例如在医疗诊断中，将病人错误地判断为健康人的代价一般比将健康人误诊为病人的代价大得多，因为前者会延误疾病的治疗，从而可能导致患者的死亡.在这样的场景中，标准的机器学习技术以最小化错误率为目标，也就隐含地假设了2种类型的分类错误造成的代价是相同的，因此训练出来的分类器就会同等地看待病人和健康人，进而增加将病人误判为健康人的可能性.由此可见，标准的机器学习技术并不适用于此类对代价敏感的应用，因此对代价敏感学习的研究就显得十分有必要了.

一般而言，代价敏感学习的目标是在给定不同类别的误分类代价时，使用训练样本学习得到一个分类器，使其在对新的未知类别的样本进行分类时，能有尽可能小的总体代价.代价敏感性广泛地存在于现实生活的各种应用中，如医疗诊断、垃圾邮件检测、网络入侵检测等等.

本文针对代价敏感问题，提出了一种新的代价敏感学习方法——代价敏感大间隔分布学习机(cost-sensitive large margin distribution machine, CS-LDM).该方法在最小化总体代价的同时对间隔分布进行优化，与传统的代价敏感支持向量机相比具有更高的性能.

1　相关工作

在过去的十几年里，研究者们围绕代价敏感学习问题进行了较为深入的研究，并得到了一系列有效的成果.在学习过程中，由于问题性质的不同，我们可能会遭遇不同类型的代价，如误分类代价、测试代价、指导代价等.其中，误分类代价在真实的应用中最为常见.误分类代价一般由专家给出，且又有2种不同的类型：基于类别的代价和基于样本的代价.在基于类别的代价中，代价只与类别有关；而在基于样本的代价中，代价与具体的样本相关.在实际应用中，基于类别的代价更易获得，因此在本文中我们也将专注于此类代价敏感问题.

在代价敏感学习中，一类通用的方法是再缩放[1-2].这种方法试图改变训练数据的分布，可以将任何以最小化错误率为目标的标准分类器转化为以最小化总体代价为目标的代价敏感分类器.针对代价敏感的二分类问题，再缩放方法已经从理论上得到了支持[1].而最近的研究成果则进一步表明，在代价敏感的多分类问题上，仅当代价矩阵满足“一致性条件”时，才有类似二分类问题的闭式解，否则需要利用任务分解后的集成学习等其他机制[2].

一般来说,有3种典型的实现再缩放的策略.

1) 加权法.不同类别中的样本被赋予不同的权值，使得高代价类别的样本具有更大的权值，从而获得代价敏感性；然后在带有权值的数据集上使用可以利用权值信息的学习方法训练标准分类器[3-4].

2) 取样法.对训练样本集进行重采样，增加高代价类别的样本数量，或减少低代价类别的样本数量，以使数据集获得代价敏感性；然后同样在改变后的数据集上训练标准分类器[1,5].

3) 阈值移动法.通过应用贝叶斯风险最小化原理，改变后验概率的决策阈值使得高代价样本不易被分错[4,6].

除了上面介绍的通用的再缩放方法外，还有一些其他的嵌入式方法通过对具体的方法进行代价敏感性设计来应对代价敏感性问题.一些常见的分类方法，如决策树、神经网络、Adaboost和支持向量机等都有其代价敏感版本[7-10].近几年，代价敏感的多类分类问题也得到了研究[2,11].

代价敏感支持向量机CS-SVM[10,12]根据不同类别的误分类代价调整形式化目标中的损失函数，从而使支持向量机的判决边界尽可能远离误分类代价较大的训练样本，以期减少高代价样本被错误地判断为其他类别的概率.

传统的支持向量机包括代价敏感支持向量机的核心思想在于最大化“最小间隔”.然而最新的研究结果显示，相比最小间隔，“间隔分布”对于降低分类器的泛化误差更加重要[13]，这一点也已经得到了证明[14].受此启发，大间隔分布学习机LDM通过同时最大化间隔均值并最小化间隔方差来优化间隔的分布，得到了更好的性能[15].

本文将大间隔分布思想应用到代价敏感学习中,提出了一种新的代价敏感分类方法CS-LDM.与CS-SVM不同的是，CS-LDM在最小化总体代价的同时，致力于对间隔的分布进行优化，并通过对偶坐标下降方法优化目标函数，以有效地进行代价敏感学习.

2　CS-LDM方法

本节首先提出CS-LDM的形式化目标，然后给出对该目标进行优化求解的算法.

2.1形式化目标

在代价敏感学习中，记输入空间为X⊂d，输出空间为Y={+1,-1}，数据则根据分布D(X,Y)独立地从样本空间中抽取.

支持向量机SVM是一类传统的大间隔学习方法，其核心思想在于最大化“最小间隔”.对于支持向量机y=wTφ(x)，样本(xi,yi)的间隔被定义为[16-17]

γi=yiwTφ(xi),∀i=1,2,…,n.

(1)

而最小间隔则是训练集中所有样本间隔的最小值.

在SVM的基础上，CS-SVM根据不同类别的误分类代价调整形式化目标中的损失函数，使误分类代价较大的训练样本拥有更大的损失函数.也就是说，CS-SVM的形式化目标如下：

(2)

在这里，ci即为第i个训练样本的误分类代价，而ciεi则是将该训练样本分错造成的损失.参数C用于权衡模型复杂度和损失.

正如第1节提到的，传统的支持向量机(包括CS-SVM)的核心思想在于最大化最小间隔.然而最新的研究结果显示，相比最小间隔，“间隔分布”对于降低分类器的泛化误差更加重要[13]，这一点也已经得到了证明[14].因此，可以利用大间隔分布思想来设计一种新的代价敏感分类方法，能够获得比代价敏感支持向量机更高的性能.

最直接的能够表示间隔分布的统计量显然应该是间隔均值和间隔方差.为了方便公式的推导，令X=[φ(x1),φ(x2),…,φ(xn)],y=[y1,y2,…,yn]T，同时令Y为n阶对角矩阵，且其对角元素为yi,…,yn.这样，可以根据式(1)计算得到训练集的间隔均值为

(3)

而间隔方差为

(4)

根据关于大间隔分布的最新理论成果[14]，可以通过同时最大化间隔均值并最小化间隔方差来优化间隔的分布.因此，在CS-SVM的基础上，我们能够进一步得到CS-LDM的形式化目标：

(5)

其中，λ1和λ2分别是用于权衡模型复杂度与间隔方差和间隔均值的参数.

2.2优化求解

将式(3)(4)代入式(5)中，可以得到

(6)

由于式(6)中包含了对间隔方差的优化，因此无法像传统的SVM那样，直接使用拉格朗日乘子法简单地求得可以应用核技巧进行优化的对偶式.幸运的是，根据表示定理[18]，式(6)的最优解应具有下面的形式：

(7)

其中，α=[α1,α2,…,αn]T是w*关于训练样本的线性表示的系数.因此有

(8)

其中K=XTX即为训练样本的核矩阵.令K:i为矩阵K的第i列向量，则式(6)可进一步改写为

(9)

其中，Q=K+4λ1(nKTK+(Ky)(Ky)T)n2，且q=-2λ2Kyn.

为式(9)中的2个约束条件分别引入拉格朗日乘子β=[β1,β2,…,βn]和μ=[μ1,μ2,…,μn]后，可以得到相应的拉格朗日函数：

(10)

对式(10)中的α和ε求偏导数，并置为0，有

(11)

(12)

将式(11)(12)代入式(10)中，即可得到式(9)的对偶形式如下:

(13)

其中，H=YKQ-1KY，Q-1是Q的逆矩阵，e为全1向量.由于式(13)中的目标优化公式为凸函数, 且约束条件为简单的箱型约束，所以能够有效地通过对偶坐标下降方法得到式(13)的最优解β*[19-20].

在得到β*后，可以根据式(11)计算出系数

α=Q-1(KYβ*-q).

(14)

由此，在对测试样本z进行分类时，其标记可以通过式(15)获得：

(15)

其中,k(·)为训练时所使用的核函数.

3　实验测试

本节首先介绍实验的设置，然后给出实验的结果，并对结果进行简单的分析.

3.1实验设置

我们在15个UCI数据集上进行了对比实验，关于数据集的具体信息由表1给出.所有样本的特征值都被规范化到[0,1]区间上.负类样本的误分类代价为1，正类样本的误分类代价取值范围为{5,10,20}.

在每个数据集上，针对每个代价取值进行10次实验.在每次测试中，将数据集中的样本随机分成3份，其中的2份用作训练集，另外1份用作测试集.我们首先在训练集上进行5-折交叉验证实验以选择参数，参数的取值范围为{0.1,1,10}，然后使用选取的参数重新训练分类器并对测试集进行分类, 最后根据分类结果计算总体代价.最终的总体代价取10次实验的均值.所有的方法都使用线性核.

Table1　Characteristics of Experimental Data Sets

在实验中，将提出的CS-LDM与以下3种分类器进行比较：1)SVM；2)LDM；3)CS-SVM.3.2节会给出这些方法的实验结果，并对结果进行分析.

3.2实验结果

表2总结了全部实验结果，并用粗体标出了在95%的置信度下进行成对t检验表现最佳的分类器.为了更直观地对实验结果进行观察，图1对CS-LDM与对比分类器在不同代价设定下的平均总体代价进行了可视化比较.其中X轴表示不同的数据集；Y轴表示不同分类器与SVM的总体代价的比值，比值越低，分类器的性能越好.最后，表3统计了CS-LDM与对比分类器进行比较的WinTieLoss结果.

从图1可以直观地看到，总体来说，2个考虑了代价的分类器CS-SVM和CS-LDM表现得显著优于传统的SVM和LDM.其中，CS-LDM的性能更加稳定，不仅在多数数据集上都有最佳表现，而且从来没有输给过其他3种分类器.

从表2可以看出，在数据集promoters，vote，haberman，isolet上，CS-LDM的结果都是一枝独秀的.但是在数据集colic.ORIG，wdbc，credit-a，german上，CS-LDM和CS-SVM的区别却并不明显.其原因可能是在这些数据集上，CS-SVM的性能已经足够好，因而CS-LDM也无法取得更好的成绩.

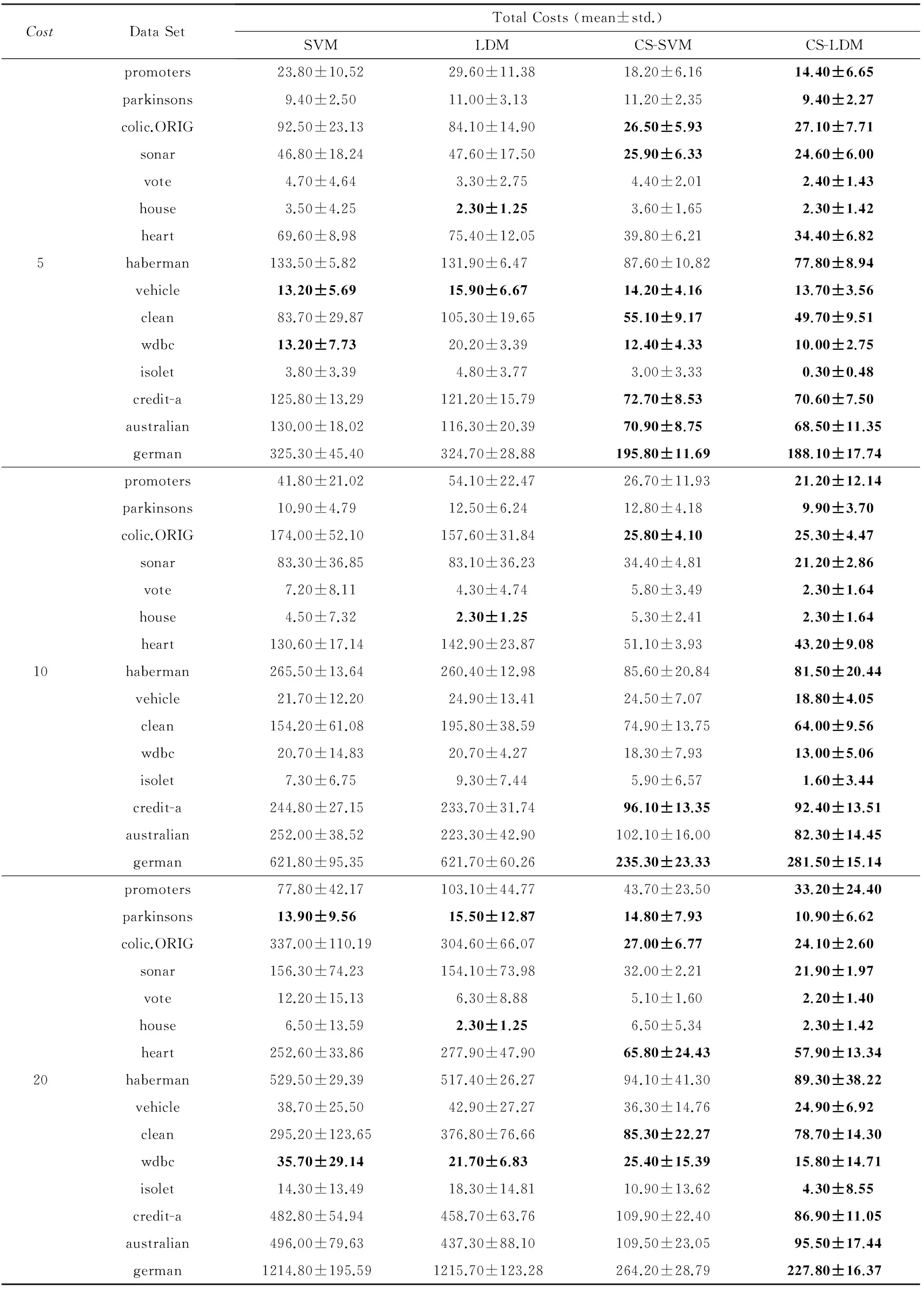
Table2　Total Costs of CS-LDM and Compared Methods

Fig. 1　Total costs of CS-LDM and compared methods.图1　CS-LDM与其他对比分类器在不同代价设定下的平均总体代价比较

Table 3WinTieLoss Counts of CS-LDM vs Compared Methods

表3CS-LDM与对比分类器进行比较的WinTieLoss结果

CostCS-LDM:Win∕Tie∕LossSVMLDMCS-SVM57∕8∕011∕4∕010∕5∕01011∕4∕011∕4∕010∕5∕0209∕6∕011∕4∕09∕6∕0

此外，通过观察图1可以发现，CS-LDM与CS-SVM的差别同LDM与SVM的差别在数据集promoters，heart，clean，isolet上并不一致.也就是说，在这些数据集上，LDM的性能要比SVM更差.之所以会出现这种现象，其原因可能在于LDM和SVM的学习目标是最小化错误率，也就隐含地假设了2类样本的误分类代价是相同的.因此，在某些数据集上，LDM为了更好地降低2类样本的整体错误率，可能会将较多的正类样本分错.然而在本文的代价敏感实验中，正类样本拥有更高的误分类代价，从而使得LDM的总体代价高于SVM.而考虑了代价敏感性的CS-LDM却不会犯同样的错误.

关于CS-LDM的性能总体上优于CS-SVM的原因，我们认为是尽管CS-LDM在代价较高的正类样本上的误分类次数与CS-SVM相差不多，但是由于CS-LDM考虑了样本间隔的分布，所以它在负类样本上的分类情况更好，进而拥有了更优的性能.根据表2中的结果可以计算得出，CS-LDM的平均总体代价比CS-SVM下降了24%.

4　结束语

在现实生活的很多应用中，对不同类别的样本错误地分类往往需要承担不同的代价.代价敏感学习的目标就是在给定不同类别的误分类代价时，使用训练样本集学习得到一个分类器，使其在对新样本进行分类时能有尽可能小的总体代价.

传统的大间隔学习方法的核心思想在于最大化最小间隔.然而最新的研究结果显示，相比最小间隔，间隔分布对于降低分类器的泛化误差更加重要.因此，本文希望用大间隔分布思想来解决代价敏感分类问题，并为此提出了CS-LDM方法.与CS-SVM不同的是，CS-LDM在最小化总体代价的同时，致力于对间隔的分布进行优化，并通过对偶坐标下降方法优化求解目标函数，以有效地进行代价敏感学习.实验结果表明，CS-LDM的性能要显著优于CS-SVM，平均总体代价下降了24%.

[1]Elkan C. The foundations of cost-sensitive learning[C]Proc of Int Joint Conf on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 2001: 973-978[2]Zhou Zhihua, Liu Xuying. On multi-class cost-sensitive learning[J]. Computational Intelligence, 2010, 26(3): 232-257[3]Ting K M. An instance-weighting method to induce cost-sensitive trees[J]. IEEE Trans on Knowledge and Data Engineering, 2002, 14(3): 659-665[4]Zhou Zhihua, Liu Xuying. Training cost-sensitive neural networks with methods addressing the class imbalance problem[J]. IEEE Trans on Knowledge and Data Engineering, 2006, 18(1): 63-77[5]Maloof M A. Learning when data sets are imbalanced and when costs are unequal and unknown[C]Proc of ICML-2003 Workshop on Learning from Imbalanced Data Sets II. Menlo Park, CA: AAAI Press, 2003[6]Jiang Shengyi, Xie Zhaoqing, Yu Wen. Naive Bayes classification algorithm based on cost sensitive for imbalanced data distribution[J]. Journal of Computer Research and Development, 2011, 48(Suppl Ⅰ): 387-390 (in Chinese)(蒋盛益, 谢照青, 余雯. 基于代价敏感的朴素贝叶斯不平衡数据分类研究[J]. 计算机研究与发展, 2011, 48(增刊Ⅰ): 387-390)[7]Bahnsen A C, Aouada D, Ottersten B. Example-dependent cost-sensitive decision trees[J]. Expert Systems with Applications, 2015, 42(19): 6609-6619[8]Ghazikhani A, Monsefi R, Yazdi H S. Online cost-sensitive neural network classifiers for non-stationary and imbalanced data streams[J]. Neural Computing & Applications, 2013, 23(5): 1283-1295[9]Fu Zhongliang. Real AdaBoost algorithm for multi-class and imbalanced classification problems[J]. Journal of Computer Research and Development, 2011, 48(12): 2326-2333 (in Chinese)(付忠良. 不平衡多分类问题的连续AdaBoost算法研究[J]. 计算机研究与发展, 2011, 48(12): 2326-2333)[10]Brefeld U, Geibel P, Wysotzki F. Support vector machines with example dependent costs[C]Proc of European Conf on Machine Learning. Berlin: Springer, 2003: 23-34[11]Raudys S, Raudys A. Pairwise costs in multiclass perceptrons[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2010, 32(7): 1324-1328[12]Qi Z, Tian Y, Shi Y, et al. Cost-sensitive support vector machine for semi-supervised learning[J]. Procedia Computer Science, 2013, 18: 1684-1689[13]Zhou Zhihua. Large margin distribution learning[M]Artificial Neural Networks in Pattern Recognition. Berlin: Springer, 2014: 1-11

[14]Gao Wei, Zhou Zhihua. On the doubt about margin explanation of boosting[J]. Artificial Intelligence, 2013, 203:1-18[15]Zhang Teng, Zhou Zhihua. Large margin distribution machine[C]Proc of ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2013: 313-322[16]Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20(3): 273-297[17]Vapnik V. The Nature of Statistical Learning Theory[M]. Berlin: Springer, 2000[18]Scholkopf B, Smola A J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond[M]. Cambridge, MA: MIT Press, 2001[19]Yuan G X, Ho C H, Lin C J. Recent advances of large-scale linear classification[J]. Proceedings of the IEEE, 2012, 100(9): 2584-2603[20]Hsieh C J, Chang K W, Lin C J, et al. A dual coordinate descent method for large-scale linear SVM[C]Proc of Int Conf on Machine Learning. New York: ACM, 2008: 408-415

Zhou Yuhang, born in 1991. Received his BSc degree in computer science and technology from Nanjing University, Nanjing, China, in 2015. MSc candidate in Nanjing University. Member of the LAMDA Group. His main research interests include machine learning and data mining.

Zhou Zhihua, born in 1973. Received his BSc, MSc and PhD degrees in computer science from Nanjing University, China, in 1996, 1998 and 2000, respectively. Professor and PhD supervisor. ACM distinguished scientist, IEEE fellow, IAPR fellow, IETIEE fellow, AAAI fellow and China Computer Federation fellow. His main research interests include artificial intelligence, machine learning, data mining, pattern recognition and multimedia information retrieval.

Cost-Sensitive Large Margin Distribution Machine

Zhou Yuhang and Zhou Zhihua

(NationalKeyLaboratoryforNovelSoftwareTechnology(NanjingUniversity),Nanjing210023)(CollaborativeInnovationCenterofNovelSoftwareTechnologyandIndustrialization,Nanjing210023)

In many real world applications, different types of misclassification often suffer from different losses, which can be described by costs. Cost-sensitive learning tries to minimize the total cost rather than minimize the error rate. During the past few years, many efforts have been devoted to cost-sensitive learning. The basic strategy for cost-sensitive learning is rescaling, which tries to rebalance the classes so that the influence of different classes is proportional to their cost, and it has been realized in different ways such as assigning different weights to training examples, resampling the training examples, moving the decision thresholds, etc. Moreover, researchers integrated cost-sensitivity into some specific methods, and proposed alternative embedded approaches such as CS-SVM. In this paper, we propose the CS-LDM (cost-sensitive large margin distribution machine) approach to tackle cost-sensitive learning problems. Rather than maximize the minimum margin like traditional support vector machines, CS-LDM tries to optimize the margin distribution and efficiently solve the optimization objective by the dual coordinate descent method, to achieve better generalization performance. Experiments on a series of data sets and cost settings exhibit the impressive performance of CS-LDM; in particular, CS-LDM is able to reduce 24% more average total cost than CS-SVM.

cost-sensitive learning; margin distribution; support vector machine (SVM); representer theorem; dual coordinate descent method

2015-06-08；

2015-09-16

国家自然科学基金项目(61333014,61321491)

周志华(zhouzh@lamda.nju.edu.cn)

TP181

This work was supported by the National Natural Science Foundation of China (61333014, 61321491).