Ti3AC2(A=Si,Al)结构、弹性和电子性质的第一性原理研究

李 辉，罗至利，刘 哲，韩旭旭，余鸿洋，孙浩东，夏晓宇，王世豪

(长安大学材料科学与工程学院， 西安 710064)



Ti3AC2(A=Si,Al)结构、弹性和电子性质的第一性原理研究

李 辉，罗至利，刘 哲，韩旭旭，余鸿洋，孙浩东，夏晓宇，王世豪

(长安大学材料科学与工程学院， 西安 710064)

采用第一性原理方法，系统地研究了MAX相材料Ti3AC2(A=Si,Al)的结构、弹性和电子性质。对比LDA和GGA计算结果可知，采用GGA近似得到的结果更接近实验值。计算分析了Ti3AC2(A=Si,Al)的弹性性质，并根据弹性常数证明了其力学稳定性。此外，还从电子态密度和Mulliken布居分析的角度考察了Ti3AC2(A=Si,Al)的电子性质和价键特性，认为其具有共价键、离子键和金属键的综合性质。本文计算结果与文献报道吻合较好。

Ti3SiC2； Ti3AlC2； 弹性性质； 电子性质； 第一性原理

1 引 言

MAX相材料是一类通式为Mn+1AXn的三元层状化合物[1,2]，其中M为过渡金属元素，A为A组元素(通常为III-A或IV-A族)，X为C或者N，n=1,2,3…。当n=2时，Mn+1AXn又简称为312相材料，主要有Ti3SiC2和Ti3AlC2等。MAX相材料通常为六方结构，过渡金属M和C或N位于A族元素所组成的六方格子的中间。特殊的结构导致这类化合物具有金属和陶瓷的双重特性，既像陶瓷一样具有耐高温、抗氧化、耐腐蚀等性能，又像金属一样具有机械可加工性、抗热震性、高温塑性、导电、导热等性能，同时还有较好的自润滑性，引起广泛关注和研究。Mn+1AXn相材料优异的性能，使其可以应用于发动机连杆、飞机燃气涡轮发动机喷嘴阀、超音速飞机、火箭发动机喷管和垫圈材料、高温热交换器等领域。

对于三元层状陶瓷Ti3AC2(A=Si,Al)，近年来已有许多研究报道。Ching等[2]采用从头计算方法对比研究了Ti3SiC2和Ti3AlC2的本征力学性质。李良等[3]对不同类型Ti3SiC2复合材料进行了综述，并对其未来发展进行了展望。尹洪峰等[4,5]报道了Ti3SiC2复合材料的制备及抗氧化性能。Xiao等[6]采用第一性原理方法研究了一系列MAX相材料的结构和电子性质，通过原子价键特性分析了其抗辐射性能，发现Ti2AlC比Ti3AlC2的抗辐射性能更好。Togo等[7]采用第一性原理方法对比研究了Ti3SiC2和Ti3AlC2的声子性质、电子性质、比热容和热膨胀性质，发现Ti3AlC2比Ti3SiC2更容易被压缩。Holm等[8]采用第一性原理方法研究了Ti3SiC2的力学性质，并考察了其在高压下的结构稳定性。Zhang等[9]采用实验和计算相结合的方法研究了Ti3AlC2在高压下的结构稳定性。Radovic等[10]研究了Ti3SiC2在300-1573 K温度范围内的弹性性质。在前期研究工作中，作者对MAX相材料Ti2SiC[11]和Ti2SiN[12]的结构、弹性和电子等性质进行了研究。

本文选择Ti3SiC2和Ti3AlC2为研究对象，采用第一性原理方法，对比研究其结构、弹性和电子性质。在第2节，简要介绍了计算方法，第3节对研究结果进行了详细讨论，最后第4节给出结论。

2 试 验

本文的第一性原理计算基于Materials Studio软件包中的CASTEP[13]量子力学程序。结构优化和性质计算时，电子与原子核离子之间的相互作用采用超软赝势[14]，其中Ti、Si、Al和C的原子赝势分别由3s23p63d24s2、3s23p2、3s23p1和2s22p2电子结构产生。原子间的交换关联作用分别采用局部密度近似(Local Density Approximation，LDA)CA-PZ泛函[15,16]和广义梯度近似(Generalized Gradient Approximation，GGA)PBE泛函[17]进行处理。原子结构优化的收敛标准为:能量偏差小于5.0×10-6eV/atom，每个原子上的力小于0.01 eV/Å，最大应力偏差小于0.02 GPa，最大位移偏差小于5.0×10-4Å。采用Monkhorst-Pack[18]取样法对每个原胞倒空间中的布里渊区进行积分，k点取样选用10×10×2的网格。电子自洽场计算(SCF)精度设为5.0×10-7eV/atom，平面波动能截断能设为400 eV。

3 结果与讨论

3.1 结构性质

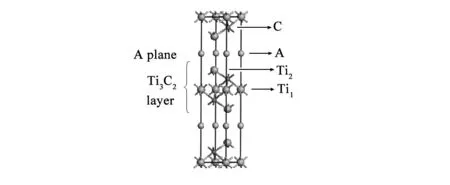
图1 Ti3AC2(A=Si,Al)的晶体结构图Fig.1 Crystal structure of Ti3AC2(A=Si,Al).

三元层状化合物Ti3AC2(A=Si,Al)属六方晶系，空间群为P63 /mmc(No.194)，每一个Ti3AC2(A=Si,Al)晶胞中含有2个Ti3AC2分子，其中6个Ti原子分别处于2a(0,0,0)和4f(1/3,2/3,0.128) Wyckoff位置，4个C原子均处于4f(1/3,2/3,0.564)位置，2个Si或Al原子处于2b(0,0,1/4)位置，其晶体结构如图1所示。紧密堆积的Ti6C八面体被由A原子形成的A平面分隔开来，C原子位于八面体的中心。Ti-C键长(Ti1-C:2.187 Å；Ti2-C:2.089 Å)较短，形成强共价键，键结合力较强，决定了其具有较高的熔点和弹性模量；A(A=Si,Al)原子层形成类似于石墨的平面(A-A键长为3.068 Å)并将Ti3C2层隔开，A-A键结合力较弱，决定了其良好的自润滑性能。这些结构特点使其兼具金属和陶瓷的双重性能。

在0 K条件下利用CASTEP软件对Ti3AC2(A=Si,Al)进行晶体结构优化，计算得到的平衡晶格常数和原胞体积见表1，并给出了与实验值和理论值的对比情况。从表1可以看出，采用LDA和GGA-PBE得到的结果略有差异，并且相对而言采用GGA近似得到的结果与实验值吻合更好。

表1 晶格常数a和c(单位Å)、原胞体积V(单位Å3/cell)的计算值与文献值的比较Tab.1 Calculated lattice parameters a,c (in Å) and volume V (in Å3),with the literature results for comparison.

3.2 弹性性质

材料的弹性常数表征了材料对外加应力的响应，或保持一个给定的变形所需要的应力。Ti3AC2(A=Si,Al)为六方晶系，根据对称性，该晶系只有5个独立的弹性常数C11、C12、C13、C33、C44。利用CASTEP软件计算得到Ti3AC2(A=Si,Al)的弹性常数如表2所示。从表2中可以看出，Ti3SiC2和Ti3AlC2的计算结果均与实验值和理论值吻合较好，并且GGA更接近实验值。C11与C33差异较大，反映了材料对不同方向的主轴应力的抵抗能力的差异，表明Ti3AC2(A=Si,Al)是各向异性材料。

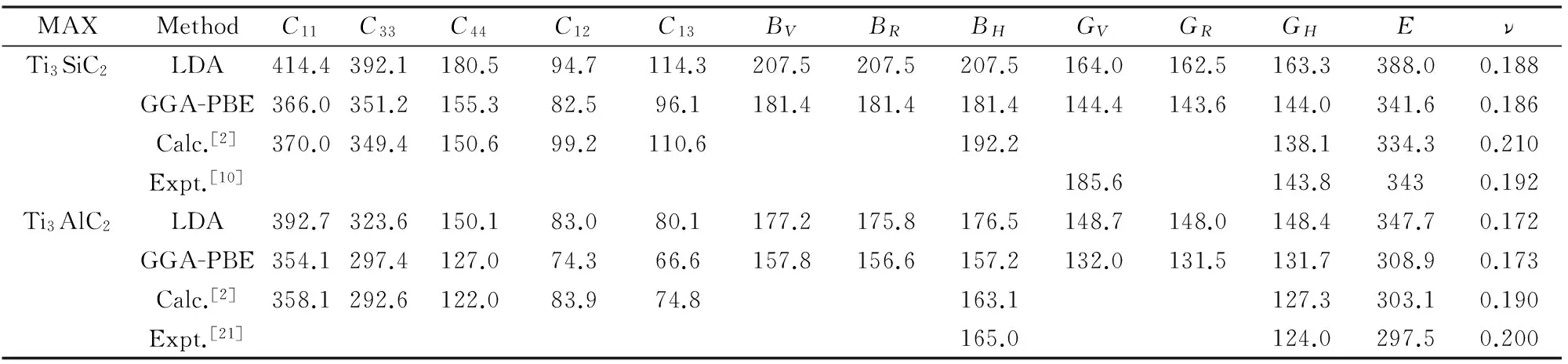
表2 Ti3AC2(A=Si,Al)的弹性常数Cij、体模量BV，BR，BH、剪切模量GV，GR，GH、杨氏模量E(单位GPa)和泊松比Tab.2 Calculated elastic constants Cij,bulk modulus BV,BR,BH,shear modulus GV,GR,GH, Young's modulus E (in GPa) and Poisson's ratio ν for Ti3AC2(A=Si,Al)

弹性常数还可以用来判断晶格的力学稳定性。对于六方晶系，相应的力学稳定性判据即波恩稳定准则[22]如公式(1)所示。由表2中结果可知，Ti3AC2(A=Si,Al)的弹性常数Cij均满足公式(1)，表明Ti3SiC2和Ti3AlC2均是力学稳定的。

(1)

根据弹性常数Cij可以计算得到Ti3AC2(A=Si,Al)的一系列弹性性质，如体积模量、剪切模量、杨氏模量和泊松系数等，计算结果也列于表2中。从表2可以看出，本文计算值与已有的文献报道吻合较好，且LDA方法计算得到的弹性性质比实验值略大，而GGA方法的计算结果比实验值稍小。此外，相对于GGA方法而言，LDA方法一般会得到较高的弹性常数和弹性模量。

体模量B表征材料抵抗压缩变形的能力，剪切模量G表征材料抵抗切应变的能力。Pugh[23]提出过一个经验判据:用剪切模量和体积模量的比值G/B来预测材料的延性和脆性，当G/B>0.57，为脆性材料，G/B越大，脆性越大；G/B<0.57材料为延性材料，G/B越小，材料韧性越好。本文中，以GGA-PBE的计算结果为例，Ti3SiC2和Ti3AlC2的G/B值分别为0.81(文献值0.7[2])和0.83(文献值0.78[2])，均大于临界值0.57，表明这两种材料均是脆性的。

除此之外，泊松比v也可以作为衡量材料韧脆性的另一个判据[23]，当泊松比小于1/3时代表材料是脆性的，泊松比约为1/3代表材料是韧性的。本文中Ti3SiC2和Ti3AlC2的泊松比均v小于1/3，同样说明Ti3SiC2和Ti3AlC2均为脆性材料，这与G/B临界值判据的结果一致。

3.3 电子性质

(1)电子态密度

电子态密度(Density of State,DOS)对理解材料的成键特性分析有重要帮助。以GGA-PBE泛函为例，计算了Ti3SiC2和Ti3AlC2的总态密度(DOS)和分波态密度(Partial Density of State,PDOS)，结果分别如图2a和图2b所示。对比图2的计算结果可知，Ti3AC2(A=Si,Al)的总态密度图可分为4个主峰:位于价带的PI、PII和PIII峰，以及位于导带的PIV峰。PI峰主要来自于C-2s态的贡献，少部分来自Ti-3d态(图2a)或Al-3p态(图2b)；PII峰主要来自于Ti-3d、A-3p和C-2p的杂化作用；PIII峰主要来自于Ti-3d和A-3p的杂化作用；位于导带的PIV峰主要来自于Ti-3d态的贡献，极少部分来自于A-3p和C-2p的贡献。原子之间的杂化作用体现了Ti3AC2(A=Si,Al)共价键的性质。对比图2a和图2b，二者的差异主要是:对Ti3SiC2而言在PI峰和PII峰之间有部分Si-3s态的贡献，并且PIII峰依附于PII峰存在；对Ti3AlC2而言PIII峰与PII峰的间隔更大一些。也许正是这些微观电子态密度的差异导致了这两种材料宏观电子性质和力学性质的不同。此外，根据图2a和图2b分析得到，Ti3SiC2和Ti3AlC2在费米面处的电子态密度计算值N(EF)分别为4.162(文献值4.02[6]和4.45[24])和3.637(文献值3.91[6]和3.83[23])electrons eV-1，可见本文计算与文献报道基本一致，并且N(EF)值均大于零，表明Ti3SiC2和Ti3AlC2均具有金属性。

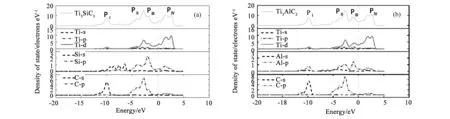
图2 总态密度和分波态密度图(a)Ti3SiC2和(b)Ti3AlC2Fig.2 Total and partial DOS(a) Ti3SiC2 and (b)Ti3AlC2.

(2)Mulliken布局分析

为了更深入的研究Ti-A-C原子间的成键性质，计算了Ti3AC2的Mulliken布局分析，以GGA-PBE的计算结果为例，结果如表3所示，给出了Ti3AC2(A=Si,Al)的轨道布居、总原子布居和原子电荷值。从表3中可以看出各个原子中轨道得失电子情况:Ti原子的2s和4s轨道失去了电子，3p和3d轨道得到了电子；A原子的3s轨道失去了电子，3p轨道得到了电子；C原子的2s轨道失去了电子，2p轨道得到了电子；综合来看，Ti原子失去了电子带正电荷，并且Ti1和Ti2原子由于位置结构的不同导致失去电子的数量也不同；A(A=Si,Al)原子和C原子得到了电子带负电荷，这个结果与原子电负性规律相吻合。表3还可以定量考核从Ti原子到C和Si原子的电荷转移数量。计算结果表明，Ti3SiC2中从Ti原子转移到Si和C原子上的电荷之和多达1.45个电子，Ti3AlC2中从Ti原子转移到Al和C原子上的电荷多达1.49个电子。这一结果是对上述电子电荷密度的定量描述，同时也表明Ti-Si-C键和Ti-Al-C键具有离子键的特性。

综合分析上述电子态密度和Mulliken布居分析的结果可以看出，Ti3SiC2和Ti3AlC2均具有共价性、离子性和金属性的综合性质。

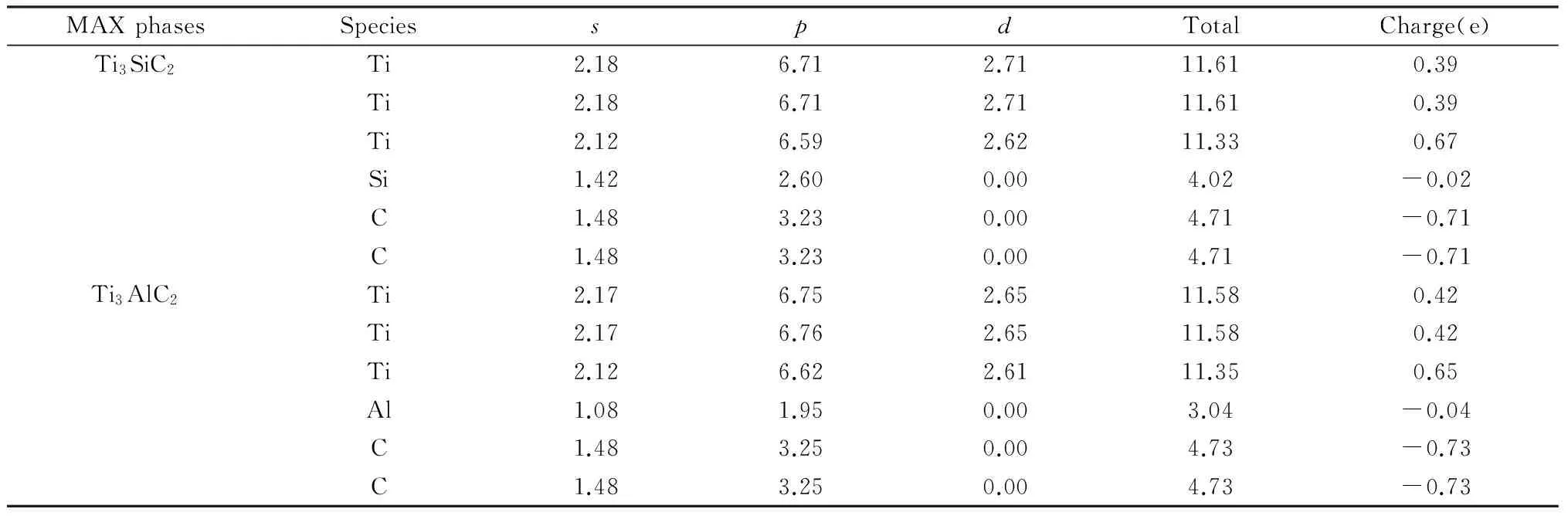
表3 Ti3AC2(A=Si,Al)的Mulliken布局分析Tab.3 Mulliken population analysis of Ti3AC2(A=Si,Al)

4 结 论

本文采用第一性原理平面波赝势方法，对比研究了Ti3SiC2和Ti3AlC2的结构、弹性和电子性质，计算结果与文献实验值和理论计算值对比较好。主要研究结果如下:

(1)考察了LDA近似和GGA近似对计算结果的影响，根据弹性常数解释了Ti3SiC2和Ti3AlC2的各向异性和力学稳定性；

(2)从电子态密度和Mulliken布居分析的角度考察了Ti3SiC2和Ti3AlC2的电子性质和价键特性，认为Ti3SiC2和Ti3AlC2均具有共价键、离子键和金属键的综合性质。

[1] Keast V J,Harris S,Smith D K.Prediction of the stability of the Mn+1AXnphases from first principles[J].Phys.Rev.B,2009,80(21):214113.

[2] Ching W-Y,Mo Y,Aryal S,et al.Intrinsic mechanical properties of 20 MAX-phase compounds[J].J.Am.Ceram.Soc.:2013,96(7),2292-2297.

[3] 李 良,周爱国.Ti3SiC2复合材料的研究进展[J].硅酸盐通报,2011,30(5):1114-1117+1141.

[4] 尹洪峰，杨祎诺.TaC/Ti3SiC2复合材料的制备与性能[J].复合材料学报,2014,(5):138-143.

[5] Xiao J,Yang T,Wang C,et al.Investigations on radiation tolerance of Mn+1AXnphases:study of Ti3SiC2,Ti3AlC2,Cr2AlC,Cr2GeC,Ti2AlC,and Ti2AlN[J].J.Am.Ceram.Soc.,2015,98(4):1323-1331.

[6] Togo A,Chaput L,Tanaka I,et al.First-principles phonon calculations of thermal expansion in Ti3SiC2,Ti3AlC2,and Ti3GeC2[J].Phys.Rev.B,2010,81(17):174301.

[7] Holm B,Ahuja R,Johansson B.Ab initio calculations of the mechanical properties of Ti3SiC2[J].Appl.Phys.Lett.,2001,79(10):1450-1452.

[8] Zhang H B,Wu X,Nickel K G,et al.High-pressure powder x-ray diffraction experiments and ab initio calculation of Ti3AlC2[J].J.Appl.Phys.,2009,106(1):013519.

[9] Radovic M,Barsoum M W,Ganguly A,et al.On the elastic properties and mechanical damping of Ti3SiC2,Ti3GeC2,Ti3Si0.5Al0.5C2and Ti2AlC in the 300-1573 K temperature range[J].Acta.Mater.,2006,54(10):2757-2767.

[10] Li H,Sun G D,Deng J L,et al.Phonon and electronic properties of Ti2SiC from first-principles calculations[J].SolidStateCommun,2015,204(0):37-40.

[11] Li H,Wang Z,Sun G,et al.First-principles study on the structural,elastic and electronic properties of Ti2SiN under high pressure[J].SolidStateCommun,2016,237-238:24-27.

[12] Clark S J,Segall M D,Pickard C J,et al.First principles methods using CASTEP[J].ZKristallogr,2005,220(5-6):567-570.

[13] Vanderbilt D.Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J].Phys.Rev.B,1990,41(11):7892-7895.

[14] Ceperley D M,Alder B J.Ground state of the electron gas by a stochastic method[J].Phys.Rev.Lett.,1980,45(7):566-569.[15] Perdew J P,Zunger A.Self-interaction correction to density-functional approximations for many-electron systems[J].Phys.Rev.B,1981,23(10):5048-5079.

[16] Perdew J P,Burke K,Ernzerhof M.Generalized gradient approximation made simple[J].Phys.Rev.Lett.,1996,77(18):3865-3868.

[17] Monkhorst H J,Pack J D.Special points for Brillouin-zone integrations[J].Phys.Rev.B,1976,13(12):5188-5192.

[18] Zhang H F,Yao B D,Shi L Q,et al.Roles of silicon-layer in Ti3SiC2materials response to helium irradiation:New insights from first-principles calculation[J].Acta.Mater.,2015,97:50-57.

[19] Sun Z M.Progress in research and development on MAX phases:a family of layered ternary compounds[J].Int.Mater.Rev.,2011,56(3):143-166.

[20] Finkel P,Barsoum M W,El-Raghy T.Low temperature dependencies of the elastic properties of Ti4AlN3,Ti3Al1.1C1.8and Ti3SiC2[J].J.Appl.Phys.,2000,87(4):1701-1703.

[21] Born M.The stability of crystal lattices[J].Proc.Camb.Philos.Soc.,1940,36:160-165.

[22] Pugh S F.Relations between the elastic moduli and the plastic properties of polycrystalline pure metals[J].Philos.Mag.,1954,45(367):823-843.

[23] Mo Y,Rulis P,Ching W Y.Electronic structure and optical conductivities of 20 MAX-phase compounds[J].Phys.Rev.B,2012,86(16):165122.

First-Principles Study on the Structural,Elastic and Electronic Properties of Ti3AC2(A=Si,Al)

LIHui,LUOZhi-li,LIUZhe,HANXu-xu,YUHong-yang,SUNHao-dong,XIAXiao-yu,WANGShi-hao

(School of Materials Science and Engineering,Chang'an University,Xi'an 710064,China)

The structural,elastic and electronic properties of MAX phase Ti3AC2(A=Si,Al) were investigated by first-principles calculations.Different exchange-correlation functionals regarding the LDA and GGA were taken into account.It is concluded that GGA method yields the best agreement with experiment results.The elastic properties of Ti3AC2(A=Si,Al) are investigated,and their structures are confirmed to be mechanically stable based on the calculated elastic constants.The electronic density of state and Mulliken population analysis have been explored to discuss the electronic properties and bonding behaviors of Ti3AC2(A=Si,Al),and their bonding nature is a combination of covalent,ionic and metallic.The present calculation results compare satisfactorily to the previous literature reports.

Ti3SiC2;Ti3AlC2;elastic property;electronic property;first-principles

国家自然科学基金(51402023、51402024)；陕西省自然科学基金(2014JQ6217、2014JQ6212)；长安大学中央高校基金(310831151081、310831152020)

李 辉(1984-)，男，博士，讲师.主要从事陶瓷、复合材料和计算材料学方面的研究.

TB332

A

1001-1625(2016)08-2341-05