基于有效集减空间逐次二次规划算法的电力系统暂态稳定约束最优潮流
2016-10-13韩其国陈功洵肖宏飞
韩其国,陈功洵,肖宏飞
基于有效集减空间逐次二次规划算法的电力系统暂态稳定约束最优潮流
韩其国1,陈功洵2,肖宏飞1
(1.杭州电子科技大学,浙江 杭州310018;2.浙江工业大学,浙江 杭州310023)
暂态稳定约束最优潮流是实现电力系统动态安全性和运行经济性协调的一种有效方式。针对已有研究中求解算法计算效率低、内存使用量大等困难,提出使用有效集减空间逐次二次规划算法求解该问题。该方法能够利用暂态稳定约束最优潮流问题中低自由度的特点,显著降低计算复杂性。引入有效集方法,在求解二次规划子问题时滤除不起作用的不等式约束,缩减子问题维度,减少了计算量。基于一系列测试算例的分析结果表明,与已有算法相比,所提算法能够有效求解大规模电力系统的暂态稳定约束最优潮流问题。
最优潮流;暂态稳定;减空间;有效集方法;逐次二次规划;微分代数方程
0 引言
动态安全性和运行经济性是坚强智能电网调度决策的目标[1]。电力系统的运行方式决定了其经济性,同时也对系统受扰后的动态安全性有着决定性的影响。已有的最优潮流(Optimal Power Flow,OPF)模型[2-5]及其拓展尽管能够有效解决电力系统稳态意义下的安全性问题,但无法保证电网经受大扰动时的动态安全性。因此,暂态稳定约束最优潮流(Transient Stability Constrained Optimal Power Flow,TSCOPF)被研究人员提出,该模型在已有OPF模型的基础上,通过集成通过微分代数方程组(Differential Algebraic Equations,DAE)形式的系统动态表述和相应的稳定判据,将暂态稳定约束作为约束条件集成到OPF模型中,从而实现了电力系统动态安全性和运行经济性的协调[6]。
TSCOPF在数学上属于DAE约束的非线性规划(Non-Linear Programming,NLP)问题,可认为是一类特殊的动态优化或最优控制问题[7]。目前已有研究主要从以下三个方面入手尝试解决该问题:
(1) 有效的DAE约束条件转化。DAE约束条件必须转化为代数方程约束才能集成到NLP问题中进行求解。文献[8]提出使用差分化的方法按仿真时间网格将DAE转化为一系列代数方程组;文献[9]则采用控制向量参数化技术将DAE仿真置于NLP求解算法外部,将暂态稳定约束转化为一个控制变量空间内的初值问题;文献[10]基于多重打靶法将上述两类算法进行融合,在NLP模型中使用边界连续条件约束保证系统状态轨迹满足稳定性能要求。
(2) 高效的NLP算法。文献[11]将内点法(Interior Point Method,IPM)引入到TSCOPF求解中,展示了较高的计算效率;文献[12]利用内点法中原-对偶系统的特点,将部分差分等式约束转化为不等式约束,实现了问题降阶;文献[12]在内点法基础上引入减空间内点法(Reduced-space IPM,RIPM),显著降低了问题求解的计算复杂度;文献[13]在该算法框架下运用极坐标形式表达潮流与转子运动方程,简化了编程难度并提升了计算效率。
(3) 简化的稳定判据。鉴于TSCOPF问题求解的复杂性,另一类研究尝试简化其中的系统动态表述及其稳定判据,从而降低TSCOPF的求解难度。此类探索包括基于拓展等面积法则(Extended Equal Area Criterion,EEAC)[14]、基于暂态稳定裕度指标[15]和基于单机无穷大母线模型(One Machine Infinite Bus,OMIB)[16]的TSCOPF算法研究。
本文从上述第(2)点进行改进,提升TSCOPF的求解效率和算法鲁棒性。减空间算法多用于化工控制等领域,多具有低自由度(Degree of freedom,DOF)的特点[17]。自由度是指控制变量的数量,即待优化变量的数量减去等式约束的数量。TSCOPF是一个典型的低自由度NLP问题,非常适合使用减空间技术求解。文献[12]首次将该技术引入TSCOPF求解,并使用高效的内点算法作为优化框架,取得了较高的计算效率。然而,在减空间内点算法中,当需要考虑的预想故障数量、仿真时步显著增加时,其零空间基矩阵的维数将随之显著增加,从而导致计算减空间海森(Reduced-space Hessian)矩阵所需的计算复杂度急剧增加,降低了该算法的计算效率。
本文在RIPM算法基础上,引入鲁棒性更强的逐次二次规划(Sequential Quadratic Programming,SQP)算法作为优化框架,提出了基于减空间逐次二次规划(Reduced-space SQP,RSQP)的TSCOPF算法,利用二次规划(Quadratic Programming,QP)子问题的特点,设计了有效集方法滤除不等式约束中不起作用的约束条件,降低了零空间基矩阵的维数增加对计算复杂性的影响,提升了算法求解效率。
1 暂态稳定约束的最优潮流
电力系统的机电暂态过程可以使用发电机摇摆方程(1)进行描述。
式中:和分别是发电机功角和电角速度;0是系统同步角速度;G、E、和分别为发电机的机械功率、电磁功率、惯性常数和阻尼系数。
使用隐式梯形积分方法对(1)进行差分化后,即可得到一系列代数方程,以此对系统经受大扰动后的功角摇摆过程进行描述。
式中,Δ为差分化时间步长,上标表示时刻的系统状态变量值。
功角稳定约束可采用相对于系统惯性中心(Center of Inertia,COI)的相对功角进行表述(3),min和max分别为相对功角的上下限值。
根据上述差分化方法,可将TSCOPF建模成为一个NLP问题,如式(4)所示。
式中:为优化变量,包括可调有功与无功源的出力值、节点电压的实部与虚部、发电机恒定电势和功角初值、以及预想故障下每个时段的功角和电角速度值;为目标函数,通常沿用OPF的目标函数,如最小化燃料成本;为等式约束,含节点稳态功率平衡约束、发电机初值方程和差分摇摆方程(2);为不等式约束,含发电机出力约束、节点电压约束、线路潮流约束和预想故障下相对功角约束(3);min和max分别为不等式约束的上下限值。
2 有效集减空间逐次二次规划算法
RSQP算法可认为是SQP算法的一种拓展[18]。本节将首先讨论SQP与RSQP算法的基本原理,然后讨论针对TSCOPF问题特点而提出的有效集方法,最后给出基于RSQP算法的TSCOPF求解流程。
2.1 SQP算法的基本原理
针对NLP问题(4),首先添加松弛变量将不等式约束转化为等式约束,将该NLP问题重写为标准形式(5)。注意此处、和的定义与式中不同。
下述讨论均针对(5)展开,设待优化变量数量为,等式约束数量为,不等式约束数量为。引入拉格朗日乘子,构造拉格朗日函数(,),上述NLP问题在最优点需要满足下述条件(6)。
使用牛顿法求解(6),在第次迭代中,需要求解搜索方向方程组(7)。
式中:∆和∆分别为第次迭代中和的搜索方向;()为雅可比矩阵;(,)为海森矩阵。
为了得到合适的搜索方向,且使更新后的原变量满足(5)中的不等式约束条件。因此可求解式(8)所示的QP子问题来逐步逼近式(5)的最优解。
由于差分后TSCOPF问题中变量较多,海森矩阵(,)的规模较大,直接采用SQP算法存在计算困难,因此可引入减空间算法减小计算规模。
2.2 减空间算法
减空间算法通过对NLP最优条件应用合适的分解策略,得到低维空间的投影海森阵,从而显著减小QP子问题的计算量。算法设计中,在牛顿迭代过程中将搜索空间分解为两个子空间:值空间和零空间,正交的基矩阵和满足下述条件[12]。
特别的,在采用坐标基分解策略时,基矩阵可采用式(11)所示策略计算。
式中:矩阵为雅可比矩阵中满秩的前列组成的∙阶矩阵;矩阵为雅可比矩阵的剩余部分,维数为∙(-);(∙)为对应维度的单位矩阵。
根据上述空间分解策略,即可将原变量的搜索方向改写为值空间投影(阶)和零空间投影(-阶)的线性组合。需要说明的是,为了简化表述,和在符号上略去,即第次迭代。
将式(9)、式(10)、式(12)代入式(7),即可得到:
在已知时,∆是的线性函数,这意味着该分解策略将原变量搜索方向上的阶搜索转换为对其零空间投影上的-阶搜索。由此,将式(12)、式(13)代入原QP子问题(8),即可得到其减空间形式(14),注意此时优化变量为,维度为-。
由此可见,减空间算法可将SQP算法中的QP子问题从维降低到-维,适合求解低自由度(即-相对较小)的NLP问题,如TSCOPF问题。
2.3 有效集方法
考察RSQP算法中的QP子问题(14),变量为-维,不等式约束为维。TSCOPF中-通常远小于,说明QP子问题的求解瓶颈在于大量不等式约束。然而在实际求解过程中,仅有少数机组发生会功角越限,大部分机组在摇摆过程中均可保在稳定,该情况在大规模系统中尤为常见,由此可运用有效集方法动态地排除不起作用的不等式约束,避免不必要的计算。反观文献[12-13]中引入的RIPM算法,由于采用了障碍函数法处理所有不等式约束,无法消去大量不起作用的约束条件,因而形成了较大的计算负担。基于上述观察,可以定义QP子问题有效约束指标函数,如式(15)所示。
该函数表征了不等式约束可能在QP子问题中起作用的几率,已越限或者靠近限值的约束条件将会获得一个大于零的值。对于函数值等于零的不等式约束,可在构造QP子问题(14)时直接忽略,因为它们在QP子问题求解中有较大几率不会成为有效约束。图1展示了该有效约束指标函数的构造原理。
图1有效集策略中的有效约束指标函数示意图
Fig. 1 Demonstration of active constraint index function in active-set strategy
在式(15)中,为警戒系数,在0至1之间取值,它定义了迭代点在何种程度接近边界时将会被认为是有效约束,即图1中警戒区间的大小。当取0时,只有已越限的约束被识别为有效约束;当取1时,全部约束均被认为是有效约束,此时该算法退化成未采用有效集方法的RSQP算法。
2.4 算法求解步骤
根据上述讨论,基于RSQP求解TSCOPF问题的步骤如下。
步骤1:读入系统数据及故障信息,生成稳态和预想故障下的节点导纳矩阵,生成初值点0;
步骤2:评估约束条件、目标函数及其雅可比矩阵和海森矩阵;
步骤3:计算子空间基矩阵和;
步骤4:计算值空间的搜索方向;
步骤5:构造QP子问题(14),应用有效约束指标滤除不起作用的不等式约束;
步骤6:求解简化后的QP子问题,获得零空间的搜索方向;
步骤7:更新原变量和拉格朗日乘子;
步骤8:判断牛顿迭代是否收敛,若满足收敛条件则输出优化结果,若不满足则跳转到步骤2。
3 算例分析
3.1 测试算例
为了验证本文所提出的RSQP算法求解TSCOPF问题的有效性,本节采用了多个标准测试算例和来自实际系统的算例进行了算例分析与测试,算例的相关信息如表1所示。可见TSCOPF问题均具有与其优化问题规模相比较低的自由度(DOF),这也正是减空间类算法能够有效提高其求解性能的理论基础。所提出的RSQP算法使用MATLAB编程实现,其中零空间基矩阵使用KLU[19]进行计算,QP子问题使用SQOPT[20]计算。相关计算性能数据均由一台配有AMD Phenom II X2 555 3.2GHz CPU和8G内存的PC机获得。
表1本文所使用的算例信息及其规模

Table 1 Summary of test cases used in this paper
本文算例均考虑单一预想故障,对于多预想故障可采用文献[11]中的方法进行处理。由于本文所关注的SQP算法仅关注NLP的高效求解,同时适用于单预想故障和多预想故障,因此暂不对多预想故障予以考虑。所设置的预想故障形式为某一传输线路发生三相对地短路0.12 s后,故障所在线路被切除;仿真时间设置为2.0 s,以此捕捉故障后完整的第一摆功角轨迹;差分化时间步长为0.02 s。相对功角的上下限取正负100度,警戒系数α取0.1。对应问题的规模如表1所示,可见随着问题规模的增加,TSCOPF的自由度始终相对较小。
3.2 算例结果分析
以IEEE39算例为例,以常规OPF和TSCOPF的优化结果作为初值点,暂态过程中发电机相对摇摆曲线如图2所示,对应的燃料成本如表2所示。
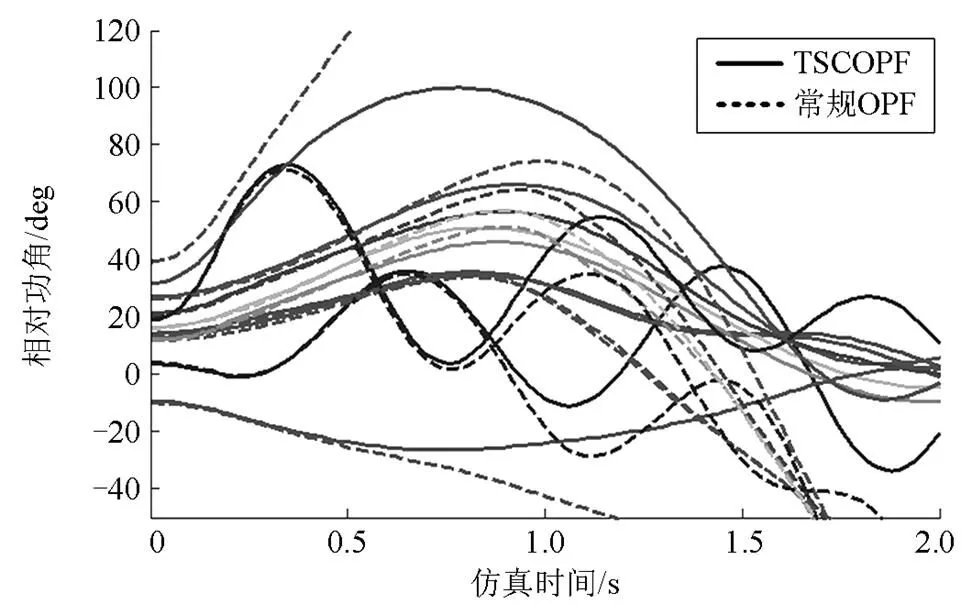
图2 IEEE39的发电机摇摆曲线

表2 IEEE39算例的计算结果
由此可见,TSCOPF能够有效的调整系统运行点,使其在预想故障的暂态过程中保持功角稳定。而常规OPF由于没有考虑相应的暂态稳定约束,因而无法保证预想故障下的系统暂态稳定性能。
3.3 算法性能比较
为了验证本文所提出算法的有效性,本节将多种NLP算法进行了横向比较,包括:全空间与减空间原-对偶内点算法(IPM和RIPM)、全空间与减空间逐次二次规划算法(SQP和RSQP)。
此项比较主要考察算法的收敛性和计算效率。前者主要由迭代次数予以考察,迭代次数少的算法可认为具有较好的收敛性;后者则主要考察计算时间,计算时间需求少的算法具有更好的实用化前景。表3展示了上述的算法性能的测试比较结果。
为了更好地进行性能比较,我们在每组算例测试中取IPM的计算时间为基准值(即1.0),给出了四种NLP算法的计算效率比较图,如图3所示。由此可见,本文提出的RSQP算法与SQP算法、IPM算法以及RIPM算法相比具有更好的收敛性和计算效率,尤其对于大规模电力系统算例,RSQP相比常规SQP算法具有超过20倍的计算性能提升,相比常用的IPM算法具有超过4倍的计算速度优势,并在收敛性能和计算效率方面均优于RIPM算法,因此非常适合TSCOPF的高效求解。
表3算法性能测试结果

Table 3 Algorithm performance test results

图3不同TSCOPF求解算法之间的计算时间比较
3.4 警戒系数取值的讨论
警戒系数的选择直接影响到QP子问题的规模和有效性。较小的会使简化的QP子问题偏离原问题,导致RSQP算法收敛性下降;较大的会使QP子问题中包含过多的不起作用不等式约束,降低算法计算效率。因此必须对进行合适的选择。
表4以IEEE162算例为例,列出了不同取值下RSQP算法的计算结果。可见随着的增加,迭代次数逐渐减少,但平均每次迭代计算时间显著增加,该系数的取值实际上体现了算法计算效率和收敛性两方面性能的折衷。由于在大规模电力系统的TSCOPF问题中,大部分不等式约束条件在迭代过程中并不起作用,选择较小的值(如表4所示的0.10)可以有效滤除不起作用的不等式约束条件,从而有效利用该问题的特点,实现在迭代次数与每次迭代计算时间之间的平衡,最小化总计算时间。
表4不同取值下IEEE162算例的TSCOPF计算结果

Table 4 TSCOPF results with different selection of α for the test case of IEEE162
4 结论
本文提出了一种基于有效集减空间逐次二次规划算法的TSCOPF求解方法。该方法能够利用TSCOPF问题中低自由度的特点,通过空间分解的形式显著降低计算复杂性;同时设计了有效集方法,有效滤除了QP子问题中不起作用的不等式约束条件,进一步降低了问题规模。通过对四个不同规模的算例进行测试,数值实验结果说明本方法能够有效求解TSCOPF问题,且与已有多种NLP算法相比具有较好的计算效率和收敛性。
[1] 汤涌, 王英涛, 田芳, 等. 大电网安全分析、预警及控制系统的研发[J]. 电网技术, 2012, 36(7): 1-11.
TANG Yong, WANG Yingtao, TIAN Fang, et al. Research and development of stability analysis, early-warning and control system for huge power grids[J]. Power System Technology, 2012, 36(7): 1-11.
[2] 高戈, 胡泽春. 含规模化储能系统的最优潮流模型与求解方法[J]. 电力系统保护与控制, 2014, 42(21): 9-16.
GAO Ge, HU Zechun. Formulation and solution method of optimal power flow with large-scale energy storage[J]. Power System Protection and Control, 2014, 42(21): 9-16.
[3] 李滨, 杜培, 韦化. 含同步风电机组的电力系统动态最优潮流[J]. 电力系统保护与控制, 2014, 41(23): 8-15.
LI Bin, DU Pei, WEI Hua. Dynamic optimal power flow considering synchronous wind generator system[J]. Power System Protection and Control, 2014, 41(23): 8-15.
[4] 杨欢, 邹斌. 含相关性随机变量的概率最优潮流问题的蒙特卡罗模拟方法[J]. 电力系统保护与控制, 2012, 40(19): 110-115.
YANG Huan, ZOU Bin. A Monte Carlo simulation method for probabilistic optimal power flow with correlated stochastic variables[J]. Power System Protection and Control, 2012, 40(19): 110-115.
[5] 刘前进, 许慧铭, 施超. 基于人工蜂群算法的多目标最优潮流问题的研究[J]. 电力系统保护与控制, 2015, 43(8): 1-7.
LIU Qianjin, XU Huiming, SHI Chao. Research on power flow optimization based on multi-objective artificial bee colony algorithm[J]. Power System Protection and Control, 2015, 43(8): 1-7.
[6] 杨新林, 孙元章, 王海风. 考虑暂态稳定性约束的最优潮流[J]. 电力系统自动化, 2003, 27(14): 13-17.
YANG Xinlin, SUN Yuanzhang, WANG Haifeng. A new approach for optimal power flow with transient stability constraints[J]. Automation of Electric Power Systems, 2003, 27(14): 13-17.
[7] BIEGLER L T. Nonlinear programming: concepts, algorithms, and applications to chemical processes[M]. Philadelphia: SIAM, 2010: 213-249.
[8] GAN D, ROBERT J T, ZIMMERMAN R D. Stability constrained optimal power flow[J]. IEEE Transactions on Power Systems, 2000, 15(2): 535-540.
[9] CHEN L, TAKA Y, OKAMOTO H, et al. Optimal operation solutions of power systems with transient stability constraints[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2001, 48(3): 327-339.
[10] GENG G, AJJARAPU V, JIANG Q. A hybrid dynamic optimization approach for stability constrained optimal power flow[J]. IEEE Transactions on Power Systems, 2014, 29(5): 2138-2149.
[11]韦化, 阳育德, 李啸骢. 多预想故障暂态稳定约束最优潮流[J]. 中国电机工程学报, 2004, 24(10): 91-96.
WEI Hua, YANG Yude, LI Xiaocong. Optimal power flow with multi-contingencies transient stability constrained[J]. Proceedings of the CSEE, 2004, 24(10): 91-96.
[12] JIANG Q, GENG G. A reduced-space interior point method for transient stability constrained optimal power flow[J]. IEEE Transactions on Power Systems, 2010, 25(3): 1232-1240.
[13]夏小琴, 韦化. 极坐标形式的暂态稳定约束最优潮流的简约空间内点法[J]. 电力系统保护与控制, 2012, 40(4): 14-19, 25.
XIA Xiaoqin, WEI Hua. A reduced-space interior point method for transient stability constrained optimal power flow in polar coordinate[J]. Power System Protection and Control, 2012, 40(4): 14-19, 25.
[14]兰强, 方勇杰, 鲍颜红, 等. 基于EEAC的考虑暂态安全稳定约束的最优潮流计算[J]. 电力系统自动化, 2010, 34(8): 34-38.
LAN Qiang, FANG Yongjie, BAO Yanhong, et al. Transient security constrained optimal power flow based on EEAC method[J]. Automation of Electric Power Systems, 2010, 34(8): 34-38.
[15]夏德明, 梅生伟, 沈沉, 等. 基于暂态稳定裕度指标的最优潮流求解[J]. 电力系统自动化, 2006, 30(24): 5-10.
XIA Deming, MEI Shengwei, SHEN Chen, et al. Computation of optimal power flow with transient stability margin index[J]. Automation of Electric Power Systems, 2006, 30(24): 5-10.
[16] PIZANO-MARTIANEZ A, FUERTE-ESQUIVEL C R, RUIZ-VEGA D. Global transient stability-constrained optimal power flow using an OMIB reference trajectory[J]. IEEE Transactions on Power Systems, 2010, 25(1): 392-403.
[17] CERVANTES A, WACHTER A, TUTUNCU R, et al. A reduced space interior point strategy for optimization of differential algebraic systems[J]. Computers and Chemical Engineering, 2000, 24(1): 39-51.
[18]袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社, 1997: 521-558.
[19] DAVIS T A, PALAMADAI NATARAJAN E. Algorithm 907: KLU, a direct sparse solver for circuit simulation problems[J]. ACM Transactions on Mathematical Software, 2010, 37(3): 36-53.
[20] GILL P E, MURRAY W, SAUNDERS M A. User guide for SQOPT 7: software for large-scale linear and quadratic programming[EB/OL]. [2008-06]. http: // web. stanford.edu/group/SOL/guides/sqdoc7.pdf.
(编辑 张爱琴)
Power system transient stability constrained optimal power flow based on active-set reduced-space sequential quadratic programming
HAN Qiguo1, CHEN Gongxun2, XIAO Hongfei1
(1. Hangzhou Dianzi University, Hangzhou 310018, China; 2. Zhejiang University of Technology, Hangzhou 310023, China)
Transient stability constrained optimal power flow (TSCOPF) is able to effectively coordinate the dynamic security and operation economics for power systems. Focusing on existing technical difficulties, including low computational efficiency and high memory consumption, this paper proposes an active-set reduced-space sequential quadratic programming algorithm to solve this problem. This approach is able to take advantage of the characteristics of few degree of freedom in TSCOPF problems, in order to decrease the computational complexity. Meanwhile, active-set technique is introduced to reduce the dimensions of quadratic programming subproblems by filtering inactive inequality constraints and reducing computational demand. Compared with existing algorithms, case studies based on a series of test cases indicate the effectiveness of the proposed approach in solving TSCOPF problems for large-scale power systems.
optimal power flow; transient stability; reduced-space method; active-set methods; sequential quadratic programming; differential algebraic equations
10.7667/PSPC151036
2015-06-22;
2015-09-17
韩其国(1963-),男,硕士,副教授,研究方向电力系统;E-mail: hanqiguo@163.com
陈功洵(1995-),男,本科生,电力系统及其自动化专业;E-mail: 1009518491@qq.com
肖宏飞(1975-),女,博士,副教授,研究方向电力系统。E-mail: xiaohongfei@hud.edu.cn
