基于软测量的水电机组功角在线测量的研究

蒋小平，雷佳玉，肖业祥

(1.中国矿业大学(北京)机电与信息工程学院，北京 100083；2.清华大学能源与动力工程系，北京 100084)

0 引言

发电机功角是电网广域监测系统三大动态稳定分析(电压稳定、频率稳定、功角稳定)的重要数据源，是表征发电机运行状态和判别电力系统安全稳定运行的主要状态变量之一。水力发电系统作为能源互联网建设中的重要组成部分，其安全稳定运行一直是电力行业的热点研究内容，通过在线监测水电机组功角的变化，可为机组在异常、故障以及失步情况下的分析及进一步的稳定控制提供重要的参考依据[1]。

功角测量从原理上分为两大类：一类是直接法测量，直接法测量在汽轮机中得到了较广泛的应用并取得了较高的测量精度，而对于极对数多、转速慢的水电机组，如果采用直接法测量需要对应每一极安装位置传感器，机械角测量产生的误差转换到电角度的误差会被放大[2]，同时由于水电机组转速低，如果像汽轮机一样在小范围内近似为匀速运动，也会产生较大的测量误差，因此直接法测量方式较难满足水电机组功角的精确测量。另一类是间接法测量，间接法的测量精度主要取决于数学模型和计算公式中参数的准确性，在稳态条件下，通过发电机的参数辨识，再根据功角定义可以计算出功角值。而当机组受到大的扰动而进入暂态过程时，由于磁饱和现象以及机组参数发生改变的影响，只能通过离线求解复杂的派克方程才可得出准确的功角值[3]。因此对水电机组功角测量方式进行改进以提高精度具有研究意义。

国内外学者对于水电机组功角测量的研究较少，且大多为直接法测量。杨永标等[4]针对水力发电机转速慢、极数多的问题，采用了一种兼顾特征大齿与均匀齿的测量方法，同时提出了频率跟踪法来应对初相角易受频率扰动影响的问题。潘琼[5]通过优化水电机组的转速测量算法来近似得到空载电势相位，从而测得功角值。而对于间接法测量功角的方式，大部分学者并没有将水电机组单独列出，并且只针对暂态过程的计算精度进行研究，忽略了稳态过程。同时由于暂态过程的计算过程比较复杂，只能通过离线的方式进行求解，难以实现准确的功角在线监测。丁孝华等[6]提出一种基于稳态分析的测量水轮机功角的暂态同步电抗折算法，但其没有考虑发电机内部除同步电抗外其他参数的影响，得出的功角值可靠性不高，且会影响稳态时的计算精度。S. Paszek等[7]提出一种基于Park变换的功角计算方法，但需要求解复杂的微分方程组，不能应用于功角的在线测量。此外，有学者研究了功角的估计与预测方法。刘俐等[8]提出基于支持向量机和长短期记忆网络的暂态功角预测方法，虽然能对故障后的功角趋势做出预测，但是其预测误差最大能达到22°，不能达到功角精确测量的要求。

针对现存的水电机组功角测量方法中直接法以及估计与预测方法误差较大，计算法在暂态过程中求解精度低，且需要求解复杂的微分方程组所造成的难以在线测量的问题，本文提出一种改进的径向基(radial basis function，RBF)神经网络功角软测量(soft sensing)在线监测方法，即采用RBF神经网络模型来映射历史电气测量值与功角的关系，并引入粒子群优化算法(particle swarm optimization，PSO)对RBF神经网络模型进行改进，同时将稳态过程中的相量图法与暂态过程中的派克方程求解法进行融合，从整体上提高了功角测量的精度，实现了功角的在线测量。该功角软测量模型采用纯电气量的测量方法，不需要在已运行的水轮发电机中进行停机改造，易于在水电机组中进行推广。

1 功角计算方法

功角δ定义为q轴的感应电势Eq与定子端电压Us的相角差，其计算方法可按照稳态与暂态过程进行分类。

1.1 稳态功角计算

同步发电机的电压-电流相量图[5]如图1所示。

图1 同步发电机的电压-电流相量图

基于图1所示相量图可以直接获得功角的计算公式：

(1)

式中：δ为功角；Xq为q轴电抗；Is为定子电流；φ为定子电压和电流之间的相角差(功率因数角)；Rs为定子电阻；Us为定子端电压。

将式(1)括号中的分子分母同时乘以视在功率S可得：

(2)

式中：P为有功功率；Q为无功功率。

在稳态过程中，根据相量图法推导得出的计算公式(2)可以很容易地计算功角值，由于功角是根据相量图直接定义的，且在稳态时同步电抗值基本保持不变，因此相量图法在稳态时求解功角具有很高的精度[3,9]。

1.2 暂态功角计算

当系统受到扰动而进入暂态过程时，机组的内部参数会发生改变，并且发电机铁芯会发生磁饱和现象，导致稳态计算方法所依赖的模型不能适用，将会导致较大的计算误差[4]。为计算发电机在暂态过程中的功角，本文采用了发电机d-q同步坐标系下的派克(Park)方程模型，该模型精确地描述了暂态过程中交流发电机的电磁相互作用关系，可以准确地计算出暂态过程的功角值[10]。具体计算过程如下：

根据同步发电机的Park方程模型可以得到关系式(3)～式(10)。

(3)

(4)

Uq=dψd-ωψq-RsId

(5)

Uq=dψq-ωψd-RsIq

(6)

(7)

(8)

(9)

(10)

将式(10)代入式(3)中，再代入式(6)，得到：

(11)

在式(11)中：

(12)

将式(7)代入式(9)，再代入式(4)和式(5)，得到：

(13)

在式(13)中：

(14)

(15)

将式(11)和式(13)分别作正序变换和逆派克变换，整理可得：

(16)

(17)

A=Ur+RsIr-ωXqIi

(18)

B=Ui+RsIi+ωXqIr

(19)

式中Ur、Ui、Ir、Ii表示定子绕组端电压与流过该绕组电流正序分量的实部值与虚部值。

根据功角和转子电角度的关系，功角可由式(20)计算：

δ=θ-θref

(20)

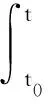
(21)

当系统受到扰动而进入暂态过程时，做出如下假设：

(1)由于次暂态开路时间常数Td0″、Tq0″很小，且定子绕组暂态和转速变化对电动势的影响可忽略不计，即dψd=0，dψq=0，以及在d、q轴的电压方程中的ω=ω0=1。那么，在式(11)、式(13)、式(16)与式(17)中的εq=εd=0，εr=εi=0。

(2)由于流过阻尼绕组Q中的IQ衰减很快，故可将其进行忽略，那么式(14)可以转化为

(22)

(3) Δω<<ω，Δω<<ωref。

首先采集水电机组的电流电压信息，采样周期为ΔT，再按照以下步骤进行计算：

(23)

sinθ=2x/(1+x2) ，cosθ=(1-x2)/(1+x2)

(24)

式中

(25)

(3)根据派克变换求解Iq(t)。

(4)用cosθ、sinθ序列乘以去调制负载波e-jωreft，然后计算上一采样周期的平均值，得出相量V1与V2，即：

(26)

(27)

式中T=2π/ωref。

根据假设条件(3)，可以认为功角δ在[t-T，t]的时间段内不发生改变，进而计算得出V1=ejδ，V2=ej(δ-π/2)，那么在每个周期采样周期计算的暂态过程的功角值为

(28)

式中arg(·)表示计算矢量的相位角。

暂态过程的功角计算方法仅在相量图法失效时的暂态过程才具有更高的计算精度，因为该方法使用了更多的发电机内部参数，并且为了求解方便对暂态过程求解时的一些影响很小的参量进行了忽略。

由于相量图法适用于稳态过程求解功角，求解派克方程法适用于暂态时求解功角，在实际运行机组中如果按照单一的求解方法进行计算，必然会影响功角的计算精度。此外由于在暂态过程时的功角计算方较复杂，且存在微分及积分计算环节，求解过程比较缓慢，难以实现水力发电机功角的在线测量。所以本文搭建了功角软测量模型，通过RBF神经网络的非线性映射关系，将两种方法进行结合。这样保证了水电机组在不同状态下的功角测量精度，同时也实现了功角的在线测量。在软测量模型搭建的过程中，RBFNN网络训练集的输入为机组中的电压、电流及功率信息，输出为根据稳态及暂态方法得出功角离线计算值，此外在电网的实际运行中，理想的稳态过程很少出现，因此将定子端电流Is在2%的范围内波动视为稳态过程，发生大于2%的波动视为暂态过程。

2 改进的RBF神经网络功角软测量模型

软测量是一种利用较易测量的辅助变量和离线分析信息去估计不可测或难测变量的方法，是近年来检测和过程控制领域出现的一种新技术，在水电机组中，可以基于易测量的电压、电流和功率信息，搭建功角的神经网络软测量模型，实现对功角的在线测量[11]。

RBF神经网络具有结构简单，学习速度快、无局部极小值的优点，理论上能逼近任意非线性函数，适合用于搭建功角的软测量模型[12-14]。同时引入PSO对RBF神经网络的参数进行寻优，以提高其训练速度及非线性逼近能力。

RBF神经网络采用高斯基函数作为其激活函数，网络的输出为

(29)

RBF神经网络训练的误差用式(30)计算：

(30)

PSO算法是一种群智能优化算法，其原理是模拟鸟类的觅食行为，通过不断更新位置和速度信息来寻求最佳觅食点，迭代公式为

(31)

式中：vi,k+1为第k+1次迭代时第i个粒子的速度；w为惯性权重，代表下一代粒子受上一代粒子的影响程度；c1和c2为加速因子，分别表示个体和社会对寻优过程的影响；r1和r2为[0,1]之间的常数；pi,k为第1个粒子在前k次迭代中得到的个体最优粒子；pg,k为前k次迭代中得到的全局最优粒子；xi,k为第k次迭代时第i个粒子的位置。

PSO算法具有优化能力强、收敛速度快等优点，广泛用于最优化问题，但在求解高维优化问题时具有易早熟的缺陷。

(32)

式中：c1s、c2s和c1e、c2e分别为加速因子c1、c2的起始值和终止值；k为当前迭代次数；K为总迭代次数。

为了提高PSO算法的求解精度，采用如式(32)所示的线性变化加速因子替换基本粒子群算法恒定加速因子。

功角软测量模型为多输入单输出模型，测量精度主要取决于RBF神经网络的基函数数据中心ci、基函数的扩展常数σj及输出权值wki。本文采用PSO算法对RBF网络参数进行优化，以提高其训练速度及软测量精度。

3 仿真模型与功角计算

为了获得软测量模型的训练集及测试集数据，本文搭建了水电机组单机无穷大系统仿真模型。在实际运行过程中，由于外部电网的电压及频率基本保持不变，可将外部电网等效为无穷大电源，并且功角值的计算均是基于某一台发电机的电气量信息，所以对于多台水力发电机同时运行的水电机组，可将其简化为单机系统进行研究[15-16]。

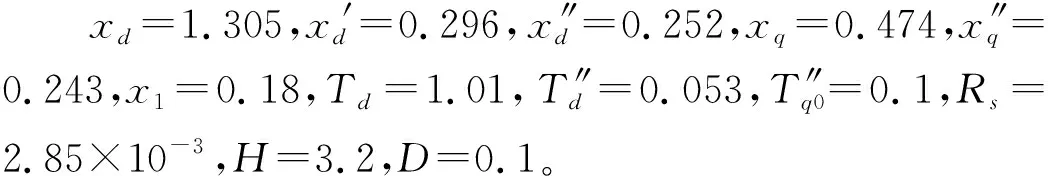
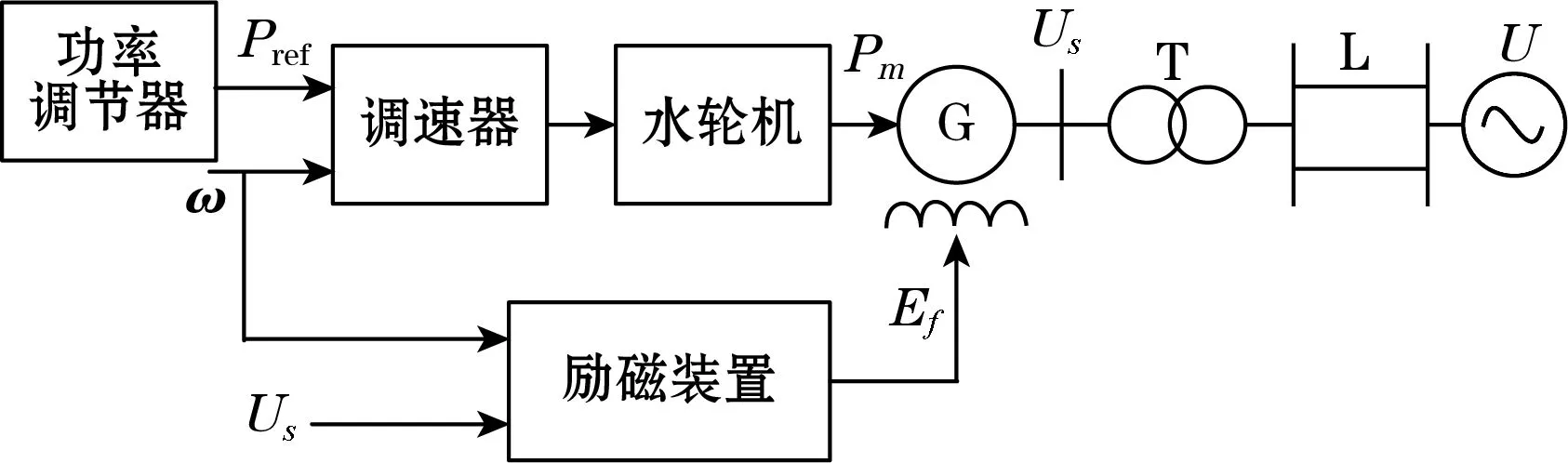
图2 单机无穷大系统

训练集和测试集利用Matlab/Simulink进行仿真及计算产生。将水电机组中输出的P、Q、Pe、If、Vs、Is作为神经网络软测量模型训练集输入，把根据功角计算方法得出的功角值作为软测量模型训练集的输出。通过改变Pm来模拟水流的变化而导致的发电机输入机械功率的变化，Pm的最大变化范围为±20%，仿真时长设定为12 s，每次变化范围递增0.5%，且在4 s后恢复到原Pm值，同时通过在输电线路的首端、20%、50%、80%及线路全长处设置单相及三相接地短路，在0.2 s后切除[8]，以此产生的水电机组响应数据及功角离线计算值作为软测量模型的训练样本。该系统共计产生了12 000组数据，其中9 600组数据作为软测量模型的训练集，2 400组数据作为测试集。本文只列出了当线路首端发生三相短路时的计算结果。

图3为当线路首端发生三相短路时，仿真输出的功角值与计算得出的功角值的对比曲线图。其中仿真输出的功角值由发电机模型的m端口得到，计算得出的功角是通过采集仿真模型输出的电压、电流、功率等数据，根据相量图法和求解派克方程法分别计算得出。可以看出在稳态过程中，计算结果与仿真结果非常相近，在暂态过程中，功角的计算结果同样能与仿真结果基本保持一致，计算误差在2.5°以内，因此可以说明所提出的功角计算方法具有较高的计算精度。

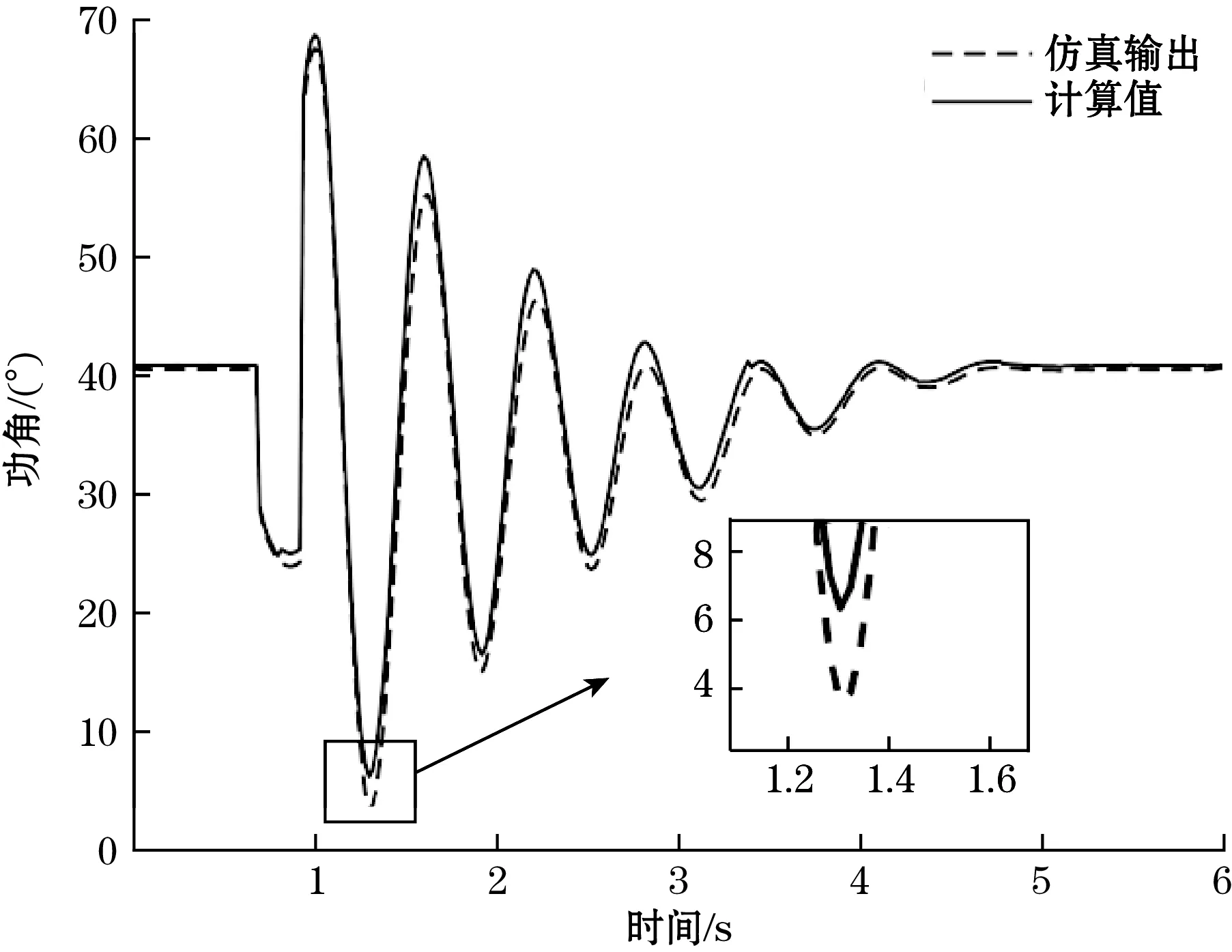
图3 线路首端三相短路时的功角值

4 软测量模型参数的确定与训练

本文采用高斯函数作为RBF神经网络的径向基函数，网络的参数包括基函数中心值ci、隐含层神经元个数、基函数的扩展常数σj及输出权值wki。可通过训练获得网络参数值。

隐含层神经元的个数决定了RBF神经网络的结构，经过多次仿真验证，在隐含层的神经元个数为9时，网络具有较好的拟合效果。网络的其他参数采用第2节提出的改进的RBF神经网络算法经过训练确定。按式(33)对粒子进行编码，取式(34)作为适应度函数。

(33)

式中：pi为第i个粒子；cj,1,i为第j个基函数中心的第1个分量；cj,2,i为第j个基函数中心的第2个分量；σj，i为第j个基函数的阈值；wj,i为第j个输出权值。

(34)

在一般的优化过程中，粒子种群规模设定为20～40之间，文中种群数设定为30，取w=0.5，c1s=2.5，c2s=0.5，c1e=0.5，c2e=2.5。训练结果表明，软测量模型均方误差(MSE)为7.155×10-5，在迭代50次左右模型误差达到最小值，训练精度及速度可以满足功角软测量的要求。

5 软测量模型的验证

为了验证训练过后软测量模型的功角测量精度及泛化能力，设置输入的机械功率Pm的幅值阶跃变化为其额定值的102.2%以及在输电线路25%处发生三相短路故障，并将系统产生的有功功率、无功功率、电磁功率、励磁电流、机端电压、机端电流输入到训练的软测量模型中，由软测量模型输出功角的测量值，并与根据计算方式得出的暂态及稳态功角值进行比较。

测量结果如图4～图7所示，当Pm发生改变时，软测量的均方误差为0.001 6；当输电线路发生三相短路时，软测量的均方误差为0.004 9。可见在单机无穷大系统中，所提出的软测量模型具有较高的测量精度。

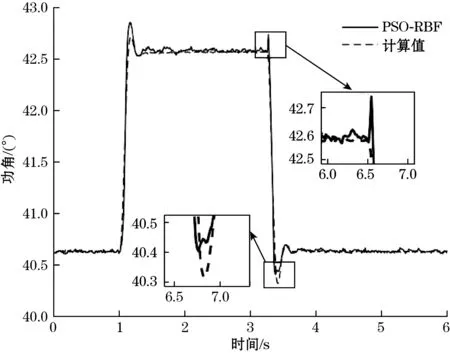
图4 Pm发生+2.2%阶跃响应4.5 s后恢复的软测量结果

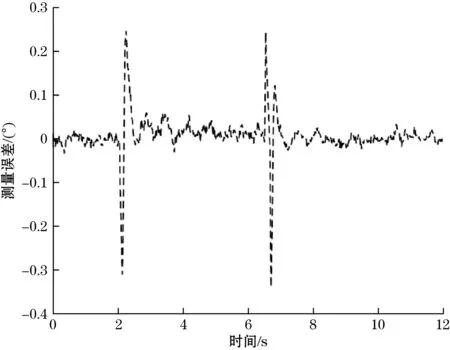
图5 Pm发生+2.2%阶跃响应4.5 s后恢复的软测量误差

图6 输电线路25%处发生三相短路0.2 s后切除的功角软测量结果

图7 输电线路25%处发生三相短路0.2 s后切除的功角软测量误差

为了验证在文中设定的所有运行状态(包括三相短路、单相短路、输入机械功率变化)中功角软测量结果的准确性，绘制了当水电机组装有自动励磁调节装置时的功角特性曲线，功角特性曲线如图8所示[17]。

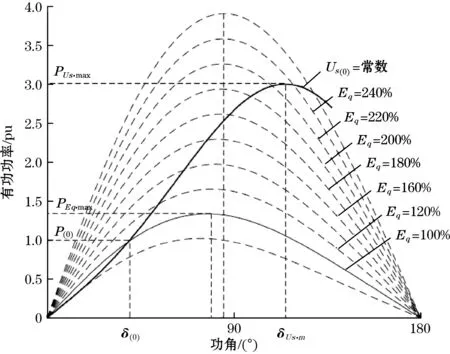
图8 带有自动励磁装置的功角特性曲线

将软测量模型所得的功角值δ和仿真模型输出的有功功率P的映射关系做出散点图，并将该散点图与功角特性曲线进行比较。在设定的所有机组运行状态中，软测量模型输出的功角在0°～80°内，将软测量模型得到的功角值按照0°～10°，10°～20°，…，70°～80°进行分组，每个区间随机抽取10组软测量值和有功功率的映射关系，并做散点图，与功角特性曲线进行对比分析，从图9中可以发现这些点大致分布在功角特性曲线附近，虽然仍具有一定的误差(与在暂态过程时不能完全保持机端电压Us为常数，绘制的功角特性曲线存在误差有关)，但也可以说明δ与P的映射关系具有与理论功角特性曲线相同的趋势，证明了所提出的功角软测量方法具有很高的可靠性。

图9 δ-P映射与功角特性曲线的关系

6 结束语

(1)针对功角测量方法在水电机组中误差较大，且在暂态过程时需要进行复杂的离线计算，不能实现功角准确的在线监测的问题，本文引入了改进的RBF软测量方法，实现了水电机组功角的在线监测。在发生三相短路与改变Pm值的验证实验中表明，软测量模型的均方误差可达到0.004 9以内，此外δ与P的映射关系也能较好地与功角特性曲线的保持一致，可以证明所提出的功角软测量模型能准确地测量出水电机组中的功角值。

(2)由于软测量模型只依赖于易测量的电气量，无需对发电机进行停机改造，可操作性高，尤其适用于极对数较多的水电机组。因此该软测量模型可以作为水电机组功角测量的一种有效的测量方式。